2020年北师大七年级数学下册第五章生活中的轴对称 单元教案
文档属性
| 名称 | 2020年北师大七年级数学下册第五章生活中的轴对称 单元教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 381.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-19 00:00:00 | ||
图片预览



文档简介
第五章
生活中的轴对称
5.1 轴对称现象
1.感知生活中的轴对称现象,探索轴对称的共同特征.
2.理解轴对称图形和两个图形关于某条直线对称的概念.
2.通过大量的实例初步认识轴对称,能识别简单的轴对称图形和成轴对称的图形及其对称轴.
自学指导 阅读教材P115~116,完成下列问题.
(一)知识探究
1.如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.
2.对称轴是一条直线,有些轴对称图形可能有几条,甚至无数条对称轴.
3.如果两个平面图形沿一条直线对折后能够完全重合,那么称这两个图形成轴对称,这条直线叫做这两个图形的对称轴.
(二)自学反馈
1.如图所示的几个图案中,是轴对称图形的是(
A
)
2.下面给出的四组图形中,成轴对称的是(
D
)
判断是否成轴对称要看是否能沿着某条直线折叠后重合.
活动1 小组讨论
例1 下列两个图形是轴对称关系的有ABC.
轴对称图形是指一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,而轴对称是两个平面图形沿一条直线对折后能够完全重合,注意两者的区别.
例2 小红将一张正方形的红纸沿对角线对折后,得到一个三角形,然后在这张重叠的纸上剪出一个非常漂亮的图案,她拿出剪出的图案问小冬,打开后的图案的对称轴至少有(
B
)
A.0条
B.1条
C.2条
D.无数条
对称轴是一条直线.
活动2 跟踪训练
1.下图中哪两个图形放在一起可以组成轴对称图形.
解:C和D,B和F.
2.观察如图所示的图案,它们都是轴对称图形,它们各有几条对称轴?在图中画出所有的对称轴.
解:(1)有2条对称轴;(2)有4条对称轴;(3)有5条对称轴;(4)有3条对称轴,
如图所示:
活动3 课堂小结
1.可用折叠判断是否为轴对称图形.
2.对称轴是一条直线,一条垂直于对应顶点连线的直线.
3.轴对称是指两个图形的位置关系,轴对称图形是指一个具有特殊形状的图形.
5.2 探索轴对称的性质
1.掌握轴对称的性质.
2.会画出已知轴对称图形的另一半.
自学指导 阅读教材P118~119,完成下列问题.
(一)知识探究
轴对称的性质:
(1)对应点所连的线段被对称轴垂直平分;
(2)对应线段相等,对应角相等.
(二)自学反馈
1.如图是轴对称图形,则相等的线段有AB=CD,BE=EC,相等的角是∠B=∠C.
2.把图中(实线部分)补成以虚线l为对称轴的轴对称图形.
解:如图所示.
可先作出各点的对称点,再顺次连接各点就得到所求图形.
活动1 小组讨论
例 如图,已知四边形ABCD与四边形EFGH关于直线MN对称,∠ABC=125°,AB=3
cm,EH=4
cm.
(1)试写出EF,AD的长度;
(2)求∠EFG的度数;
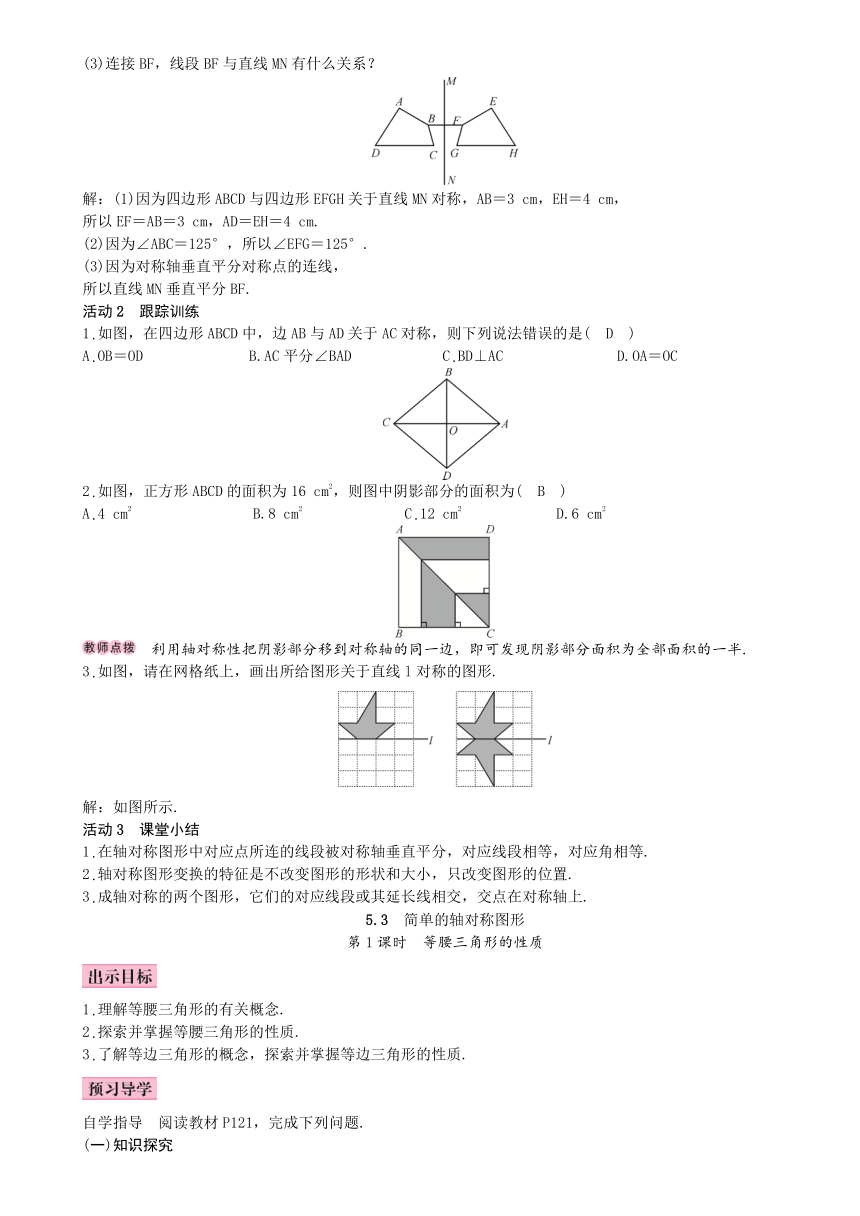
(3)连接BF,线段BF与直线MN有什么关系?
解:(1)因为四边形ABCD与四边形EFGH关于直线MN对称,AB=3
cm,EH=4
cm,
所以EF=AB=3
cm,AD=EH=4
cm.
(2)因为∠ABC=125°,所以∠EFG=125°.
(3)因为对称轴垂直平分对称点的连线,
所以直线MN垂直平分BF.
活动2 跟踪训练
1.如图,在四边形ABCD中,边AB与AD关于AC对称,则下列说法错误的是(
D
)
A.OB=OD B.AC平分∠BAD
C.BD⊥AC
D.OA=OC
2.如图,正方形ABCD的面积为16
cm2,则图中阴影部分的面积为(
B
)
A.4
cm2
B.8
cm2
C.12
cm2
D.6
cm2
利用轴对称性把阴影部分移到对称轴的同一边,即可发现阴影部分面积为全部面积的一半.
3.如图,请在网格纸上,画出所给图形关于直线l对称的图形.
解:如图所示.
活动3 课堂小结
1.在轴对称图形中对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.
2.轴对称图形变换的特征是不改变图形的形状和大小,只改变图形的位置.
3.成轴对称的两个图形,它们的对应线段或其延长线相交,交点在对称轴上.
5.3 简单的轴对称图形
第1课时 等腰三角形的性质
1.理解等腰三角形的有关概念.
2.探索并掌握等腰三角形的性质.
3.了解等边三角形的概念,探索并掌握等边三角形的性质.
自学指导 阅读教材P121,完成下列问题.
(一)知识探究
1.等腰三角形是轴对称图形.
2.等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
3.等腰三角形的两个底角相等.
4.等边三角形有三条对称轴,等边三角形每条边都相等.
(二)自学反馈
1.下列说法中,正确的有(
D
)
①等腰三角形的两腰相等;②等腰三角形的两底角相等;③等腰三角形底边上的中线与底边上的高相等;④等腰三角形是轴对称图形.
A.1个
B.2个
C.3个
D.4个
2.△ABC中,AB=AC.
(1)若∠B=45°,则∠A=90°,∠C=45°;
(2)若∠C=60°,则∠A=60°,∠B=60°.
活动1 小组讨论
例1 如图,在△ABC中,AB=AC,∠A=40°,BD是∠ABC的平分线,求∠BDC的度数.
解:因为AB=AC,∠A=40°,
所以∠ABC=∠C==70°.
因为BD是∠ABC的平分线,
所以∠DBC=∠ABC=35°.
所以∠BDC=180°-∠DBC-∠C=75°.
例2 如图,在一条河的同岸有两个村庄A和B,两村要在河上合修一座便民桥,桥修在什么地方可以使桥到两村的距离之和最短?
解:如图,作点A关于河岸的对称点C,连接BC交河岸于点P,点P就是桥的位置.
理由:两点之间线段最短.
在解决最短路径问题时,我们通常利用轴对称、平移等变换把已知问题转化为容易解决的问题,从而作出最短路径的选择.
活动2 跟踪训练
1.如图,△ABC中,AC=BC,直线经过点C,则下列说法正确的是(
D
)
A.垂直AB
B.平分AB
C.垂直平分AB
D.与AB的关系不能确定
2.已知等腰三角形的顶角为80°,那么它的一个底角为50°.
3.如图,P,Q是△ABC的边BC上的两点,且BP=PQ=QC=AP=AQ,求∠BAC的度数.
解:因为PA=PQ=AQ,
所以∠APQ=∠PQA=∠QAP=60°.
因为PA=PB,
所以∠B=∠PAB.
又因为∠B+∠PAB=180°-∠APB=180-(180°-∠APQ)=60°,
所以∠PBA=∠PAB=30°.同理∠QAC=30°.
所以∠BAC=∠BAP+∠PAQ+∠QAC
=30°+60°+30°
=120°.
活动3 课堂小结
在等腰三角形中,常常需要作底边上的高,运用等腰三角形“三线合一”的性质,对于解决相关问题能起到事半功倍的效果.对于等边三角形,它属于特殊的等腰三角形,“三线合一”的性质就更能不受限制,淋漓尽致地发挥了.
第2课时 线段垂直平分线的性质及画法
1.经历探索简单图形轴对称性的过程,进一步体会轴对称的特征,发展空间观念.
2.探索并掌握线段垂直平分线的有关性质.
自学指导 阅读教材P123~P124,完成下列问题.
(一)知识探究
1.线段是轴对称图形,垂直并且平分线段的直线是它的一条对称轴.
2.线段垂直平分线上的点到这条线段两个端点的距离相等.
(二)自学反馈
1.如图,直线CD是线段AB的垂直平分线,P是直线CD上的一点.已知线段PA=5,则线段PB的长度为(
B
)
A.6
B.5
C.4
D.3
2.如图,在△ABC中,分别以点A,B为圆心,大于AB的长为半径画弧,两弧分别交于点D,E,则直线DE是(
D
)
A.∠A的平分线
B.AC边的中线
C.BC边的高线
D.AB边的垂直平分线
活动1 小组讨论
例1 如图,在△ABC中,DE是AC的垂直平分线,AE=3
cm,△ABD的周长为13
cm,求△ABC的周长.
解:因为DE是AC的垂直平分线,
所以AD=CD,AC=2AE=6(cm).
因为△ABD的周长为13
cm,
所以AB+BD+AD=AB+BD+DC=AB+BC=13
cm.
所以△ABC的周长为AB+BC+AC=13+6=19(cm).
由垂直平分线的性质得AD=DC,再通过线段之间的等量代换即可得出△ABC的周长.
例2 某旅游景区内有一块三角形绿地ABC,如图所示,现要在道路AB的边缘上建一个休息点M,使它到A,C两个点的距离相等.在图中确定休息点M的位置.
解:作AC的垂直平分线交AB于M点,则点M即为所求.
活动2 跟踪训练
1.如图,已知直线MN是线段AB的中垂线,垂足为N,AM=5
cm,△MAB的周长为16
cm,那么AN等于(
A
)
A.3
cm
B.4
cm
C.5
cm
D.6
cm
2.如图,在已知的△ABC中,按以下步骤作图:
①分别以B,C为圆心,大于BC的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.
若CD=AC,∠A=50°,则∠ACB的度数为(
D
)
A.90°
B.95°
C.100°
D.105°
活动3 课堂小结
本课时主要学些了哪些知识与方法,有何收获和感悟?
(1)线段的轴对称性:线段是轴对称图形.
(2)线段的垂直平分线的性质
(3)线段垂直平分线的作图.
第3课时 角平分线的性质及画法
1.经历探索简单图形轴对称性的过程,进一步体会轴对称的特征,发展空间观念.
2.探索并掌握角平分线的有关性质.
自学指导 阅读教材P125~P126,完成下列问题.
(一)知识探究
1.角是轴对称图形,角平分线所在的直线是它的对称轴.
2.角平分线上的点到这个角的两边的距离相等.
(二)自学反馈
1.下列图形中,不是轴对称图形的是(
D
)
A.角 B.等边三角形
C.线段
D.直角三角形
2.如图,CD⊥OA,CE⊥OB,D,E为垂足.
(1)若∠1=∠2,则有CD=CE;
(2)若CD=CE,则有∠1=∠2.
活动1 小组讨论
例1 如图,已知AO平分∠BAC,OE⊥AB,OD⊥AC.试说明:OE=OD.
解:因为AO平分∠BAC,OE⊥AB,OD⊥AC,
所以OE=OD(角平分线上的点到角两边的距离相等).
角平分线的性质是说明线段相等的另一个途径,其前提条件有两条:(1)角平分线;(2)垂直.
例2 如图,已知线段a和∠AOB.
(1)在OA边上作点P,使OP=2a;
(2)作∠AOB的平分线.
解:(1)点P为所求作.
(2)OC为所求作.
角平分线的作图依据是“SSS”.
活动2 跟踪训练
1.如图,OE平分∠AOB,EC⊥OA于点C,ED⊥OB于点D,ED与EC的长度关系为(
B
)
A.ED>EC
B.ED=EC
C.ED<EC
D.无法确定
2.如图,已知∠AOB.小明按如下步骤作图:
①在OA和OB上分别截取OD,OE,使OD=OE;
②分别以D,E为圆心,大于DE的长为半径作弧,两弧在∠AOB的内部交于点C;
③作射线OC.
根据上述作图步骤,回答下列问题:
(1)写出一个正确的结论:OC为∠AOB的平分线;
(2)如果在OC上任取一点M,那么点M到OA,OB的距离相等.
依据是角平分线上的点到这个角的两边的距离相等.
活动3 课堂小结
在已知角平分线的条件下,常想到过角平分线上的点向角两边作垂线段的方法,在已知角平分线的条件下,也可想到翻折的方法.
5.4 利用轴对称进行设计
1.经历对图形进行观察、分析、欣赏和动手操作、画图的过程,掌握有关画图的操作技能,发展初步审美能力,增强对图形欣赏的意识.
2.能按要求把所给出的图形补成以某条直线为对称轴的轴对称图形,能依据图形的轴对称关系设计轴对称图形.
自学指导 阅读教材P128~129,完成下列问题.
(一)知识探究
轴对称的性质:
在轴对称图形中:(1)对应点所连的线段被对称轴垂直平分;(2)对应线段相等,对应角相等.
(二)自学反馈
要在一块长方形的空地上修建一个共坛,要求花坛图案为轴对称图形,图中的设计符合要求的有(
A
)
A.4个
B.3个
C.2个
D.1个
活动1 小组讨论
例1 如图,直线是一个轴对称图形的对称轴,画出这个轴对称图形的另一半.
题图
答案图
解:如图所示.
例2 如图甲,正方形被划分成16个全等的三角形,将其中若干个三角形涂黑,且满足下列条件:
(1)涂黑部分的面积是原正方形面积的一半;
(2)涂黑部分成轴对称图形.如图乙是一种涂法,请在图1~3中分别设计另外三种涂法.(在所设计的图案中,若涂黑部分全等,则认为是同一种涂法,如图乙与图丙)
解:不同涂法的图案例举如下.
活动2 跟踪训练
把下列各图补成以l为对称轴的轴对称图形.
解:如图所示.
活动3 课堂小结
本节课学习了已知对称轴和一个点如何画出它的对应点,以及如何补全图形,并利用轴对称的性质知道如何设计轴对称图形.
生活中的轴对称
5.1 轴对称现象
1.感知生活中的轴对称现象,探索轴对称的共同特征.
2.理解轴对称图形和两个图形关于某条直线对称的概念.
2.通过大量的实例初步认识轴对称,能识别简单的轴对称图形和成轴对称的图形及其对称轴.
自学指导 阅读教材P115~116,完成下列问题.
(一)知识探究
1.如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.
2.对称轴是一条直线,有些轴对称图形可能有几条,甚至无数条对称轴.
3.如果两个平面图形沿一条直线对折后能够完全重合,那么称这两个图形成轴对称,这条直线叫做这两个图形的对称轴.
(二)自学反馈
1.如图所示的几个图案中,是轴对称图形的是(
A
)
2.下面给出的四组图形中,成轴对称的是(
D
)
判断是否成轴对称要看是否能沿着某条直线折叠后重合.
活动1 小组讨论
例1 下列两个图形是轴对称关系的有ABC.
轴对称图形是指一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,而轴对称是两个平面图形沿一条直线对折后能够完全重合,注意两者的区别.
例2 小红将一张正方形的红纸沿对角线对折后,得到一个三角形,然后在这张重叠的纸上剪出一个非常漂亮的图案,她拿出剪出的图案问小冬,打开后的图案的对称轴至少有(
B
)
A.0条
B.1条
C.2条
D.无数条
对称轴是一条直线.
活动2 跟踪训练
1.下图中哪两个图形放在一起可以组成轴对称图形.
解:C和D,B和F.
2.观察如图所示的图案,它们都是轴对称图形,它们各有几条对称轴?在图中画出所有的对称轴.
解:(1)有2条对称轴;(2)有4条对称轴;(3)有5条对称轴;(4)有3条对称轴,
如图所示:
活动3 课堂小结
1.可用折叠判断是否为轴对称图形.
2.对称轴是一条直线,一条垂直于对应顶点连线的直线.
3.轴对称是指两个图形的位置关系,轴对称图形是指一个具有特殊形状的图形.
5.2 探索轴对称的性质
1.掌握轴对称的性质.
2.会画出已知轴对称图形的另一半.
自学指导 阅读教材P118~119,完成下列问题.
(一)知识探究
轴对称的性质:
(1)对应点所连的线段被对称轴垂直平分;
(2)对应线段相等,对应角相等.
(二)自学反馈
1.如图是轴对称图形,则相等的线段有AB=CD,BE=EC,相等的角是∠B=∠C.
2.把图中(实线部分)补成以虚线l为对称轴的轴对称图形.
解:如图所示.
可先作出各点的对称点,再顺次连接各点就得到所求图形.
活动1 小组讨论
例 如图,已知四边形ABCD与四边形EFGH关于直线MN对称,∠ABC=125°,AB=3
cm,EH=4
cm.
(1)试写出EF,AD的长度;
(2)求∠EFG的度数;
(3)连接BF,线段BF与直线MN有什么关系?
解:(1)因为四边形ABCD与四边形EFGH关于直线MN对称,AB=3
cm,EH=4
cm,
所以EF=AB=3
cm,AD=EH=4
cm.
(2)因为∠ABC=125°,所以∠EFG=125°.
(3)因为对称轴垂直平分对称点的连线,
所以直线MN垂直平分BF.
活动2 跟踪训练
1.如图,在四边形ABCD中,边AB与AD关于AC对称,则下列说法错误的是(
D
)
A.OB=OD B.AC平分∠BAD
C.BD⊥AC
D.OA=OC
2.如图,正方形ABCD的面积为16
cm2,则图中阴影部分的面积为(
B
)
A.4
cm2
B.8
cm2
C.12
cm2
D.6
cm2
利用轴对称性把阴影部分移到对称轴的同一边,即可发现阴影部分面积为全部面积的一半.
3.如图,请在网格纸上,画出所给图形关于直线l对称的图形.
解:如图所示.
活动3 课堂小结
1.在轴对称图形中对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.
2.轴对称图形变换的特征是不改变图形的形状和大小,只改变图形的位置.
3.成轴对称的两个图形,它们的对应线段或其延长线相交,交点在对称轴上.
5.3 简单的轴对称图形
第1课时 等腰三角形的性质
1.理解等腰三角形的有关概念.
2.探索并掌握等腰三角形的性质.
3.了解等边三角形的概念,探索并掌握等边三角形的性质.
自学指导 阅读教材P121,完成下列问题.
(一)知识探究
1.等腰三角形是轴对称图形.
2.等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴.
3.等腰三角形的两个底角相等.
4.等边三角形有三条对称轴,等边三角形每条边都相等.
(二)自学反馈
1.下列说法中,正确的有(
D
)
①等腰三角形的两腰相等;②等腰三角形的两底角相等;③等腰三角形底边上的中线与底边上的高相等;④等腰三角形是轴对称图形.
A.1个
B.2个
C.3个
D.4个
2.△ABC中,AB=AC.
(1)若∠B=45°,则∠A=90°,∠C=45°;
(2)若∠C=60°,则∠A=60°,∠B=60°.
活动1 小组讨论
例1 如图,在△ABC中,AB=AC,∠A=40°,BD是∠ABC的平分线,求∠BDC的度数.
解:因为AB=AC,∠A=40°,
所以∠ABC=∠C==70°.
因为BD是∠ABC的平分线,
所以∠DBC=∠ABC=35°.
所以∠BDC=180°-∠DBC-∠C=75°.
例2 如图,在一条河的同岸有两个村庄A和B,两村要在河上合修一座便民桥,桥修在什么地方可以使桥到两村的距离之和最短?
解:如图,作点A关于河岸的对称点C,连接BC交河岸于点P,点P就是桥的位置.
理由:两点之间线段最短.
在解决最短路径问题时,我们通常利用轴对称、平移等变换把已知问题转化为容易解决的问题,从而作出最短路径的选择.
活动2 跟踪训练
1.如图,△ABC中,AC=BC,直线经过点C,则下列说法正确的是(
D
)
A.垂直AB
B.平分AB
C.垂直平分AB
D.与AB的关系不能确定
2.已知等腰三角形的顶角为80°,那么它的一个底角为50°.
3.如图,P,Q是△ABC的边BC上的两点,且BP=PQ=QC=AP=AQ,求∠BAC的度数.
解:因为PA=PQ=AQ,
所以∠APQ=∠PQA=∠QAP=60°.
因为PA=PB,
所以∠B=∠PAB.
又因为∠B+∠PAB=180°-∠APB=180-(180°-∠APQ)=60°,
所以∠PBA=∠PAB=30°.同理∠QAC=30°.
所以∠BAC=∠BAP+∠PAQ+∠QAC
=30°+60°+30°
=120°.
活动3 课堂小结
在等腰三角形中,常常需要作底边上的高,运用等腰三角形“三线合一”的性质,对于解决相关问题能起到事半功倍的效果.对于等边三角形,它属于特殊的等腰三角形,“三线合一”的性质就更能不受限制,淋漓尽致地发挥了.
第2课时 线段垂直平分线的性质及画法
1.经历探索简单图形轴对称性的过程,进一步体会轴对称的特征,发展空间观念.
2.探索并掌握线段垂直平分线的有关性质.
自学指导 阅读教材P123~P124,完成下列问题.
(一)知识探究
1.线段是轴对称图形,垂直并且平分线段的直线是它的一条对称轴.
2.线段垂直平分线上的点到这条线段两个端点的距离相等.
(二)自学反馈
1.如图,直线CD是线段AB的垂直平分线,P是直线CD上的一点.已知线段PA=5,则线段PB的长度为(
B
)
A.6
B.5
C.4
D.3
2.如图,在△ABC中,分别以点A,B为圆心,大于AB的长为半径画弧,两弧分别交于点D,E,则直线DE是(
D
)
A.∠A的平分线
B.AC边的中线
C.BC边的高线
D.AB边的垂直平分线
活动1 小组讨论
例1 如图,在△ABC中,DE是AC的垂直平分线,AE=3
cm,△ABD的周长为13
cm,求△ABC的周长.
解:因为DE是AC的垂直平分线,
所以AD=CD,AC=2AE=6(cm).
因为△ABD的周长为13
cm,
所以AB+BD+AD=AB+BD+DC=AB+BC=13
cm.
所以△ABC的周长为AB+BC+AC=13+6=19(cm).
由垂直平分线的性质得AD=DC,再通过线段之间的等量代换即可得出△ABC的周长.
例2 某旅游景区内有一块三角形绿地ABC,如图所示,现要在道路AB的边缘上建一个休息点M,使它到A,C两个点的距离相等.在图中确定休息点M的位置.
解:作AC的垂直平分线交AB于M点,则点M即为所求.
活动2 跟踪训练
1.如图,已知直线MN是线段AB的中垂线,垂足为N,AM=5
cm,△MAB的周长为16
cm,那么AN等于(
A
)
A.3
cm
B.4
cm
C.5
cm
D.6
cm
2.如图,在已知的△ABC中,按以下步骤作图:
①分别以B,C为圆心,大于BC的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.
若CD=AC,∠A=50°,则∠ACB的度数为(
D
)
A.90°
B.95°
C.100°
D.105°
活动3 课堂小结
本课时主要学些了哪些知识与方法,有何收获和感悟?
(1)线段的轴对称性:线段是轴对称图形.
(2)线段的垂直平分线的性质
(3)线段垂直平分线的作图.
第3课时 角平分线的性质及画法
1.经历探索简单图形轴对称性的过程,进一步体会轴对称的特征,发展空间观念.
2.探索并掌握角平分线的有关性质.
自学指导 阅读教材P125~P126,完成下列问题.
(一)知识探究
1.角是轴对称图形,角平分线所在的直线是它的对称轴.
2.角平分线上的点到这个角的两边的距离相等.
(二)自学反馈
1.下列图形中,不是轴对称图形的是(
D
)
A.角 B.等边三角形
C.线段
D.直角三角形
2.如图,CD⊥OA,CE⊥OB,D,E为垂足.
(1)若∠1=∠2,则有CD=CE;
(2)若CD=CE,则有∠1=∠2.
活动1 小组讨论
例1 如图,已知AO平分∠BAC,OE⊥AB,OD⊥AC.试说明:OE=OD.
解:因为AO平分∠BAC,OE⊥AB,OD⊥AC,
所以OE=OD(角平分线上的点到角两边的距离相等).
角平分线的性质是说明线段相等的另一个途径,其前提条件有两条:(1)角平分线;(2)垂直.
例2 如图,已知线段a和∠AOB.
(1)在OA边上作点P,使OP=2a;
(2)作∠AOB的平分线.
解:(1)点P为所求作.
(2)OC为所求作.
角平分线的作图依据是“SSS”.
活动2 跟踪训练
1.如图,OE平分∠AOB,EC⊥OA于点C,ED⊥OB于点D,ED与EC的长度关系为(
B
)
A.ED>EC
B.ED=EC
C.ED<EC
D.无法确定
2.如图,已知∠AOB.小明按如下步骤作图:
①在OA和OB上分别截取OD,OE,使OD=OE;
②分别以D,E为圆心,大于DE的长为半径作弧,两弧在∠AOB的内部交于点C;
③作射线OC.
根据上述作图步骤,回答下列问题:
(1)写出一个正确的结论:OC为∠AOB的平分线;
(2)如果在OC上任取一点M,那么点M到OA,OB的距离相等.
依据是角平分线上的点到这个角的两边的距离相等.
活动3 课堂小结
在已知角平分线的条件下,常想到过角平分线上的点向角两边作垂线段的方法,在已知角平分线的条件下,也可想到翻折的方法.
5.4 利用轴对称进行设计
1.经历对图形进行观察、分析、欣赏和动手操作、画图的过程,掌握有关画图的操作技能,发展初步审美能力,增强对图形欣赏的意识.
2.能按要求把所给出的图形补成以某条直线为对称轴的轴对称图形,能依据图形的轴对称关系设计轴对称图形.
自学指导 阅读教材P128~129,完成下列问题.
(一)知识探究
轴对称的性质:
在轴对称图形中:(1)对应点所连的线段被对称轴垂直平分;(2)对应线段相等,对应角相等.
(二)自学反馈
要在一块长方形的空地上修建一个共坛,要求花坛图案为轴对称图形,图中的设计符合要求的有(
A
)
A.4个
B.3个
C.2个
D.1个
活动1 小组讨论
例1 如图,直线是一个轴对称图形的对称轴,画出这个轴对称图形的另一半.
题图
答案图
解:如图所示.
例2 如图甲,正方形被划分成16个全等的三角形,将其中若干个三角形涂黑,且满足下列条件:
(1)涂黑部分的面积是原正方形面积的一半;
(2)涂黑部分成轴对称图形.如图乙是一种涂法,请在图1~3中分别设计另外三种涂法.(在所设计的图案中,若涂黑部分全等,则认为是同一种涂法,如图乙与图丙)
解:不同涂法的图案例举如下.
活动2 跟踪训练
把下列各图补成以l为对称轴的轴对称图形.
解:如图所示.
活动3 课堂小结
本节课学习了已知对称轴和一个点如何画出它的对应点,以及如何补全图形,并利用轴对称的性质知道如何设计轴对称图形.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
