人教版九年级数学上册22.3实际问题与二次函数第3课时——拱桥问题和运动中的抛物线课件(共18张PPT)
文档属性
| 名称 | 人教版九年级数学上册22.3实际问题与二次函数第3课时——拱桥问题和运动中的抛物线课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-19 00:00:00 | ||
图片预览



文档简介
(共18张PPT)
第二十二章
二次函数
22.3
实际问题与二次函数
第3课时
拱桥问题和运动中的抛物线
灵宝市秦岭学校
九年级数学组
1
会建立二次函数模型,把实际问题转化为二次函数问题.(重点)
2
利用二次函数解决拱桥及运动中的有关问题.
(重、难点)
学习目标
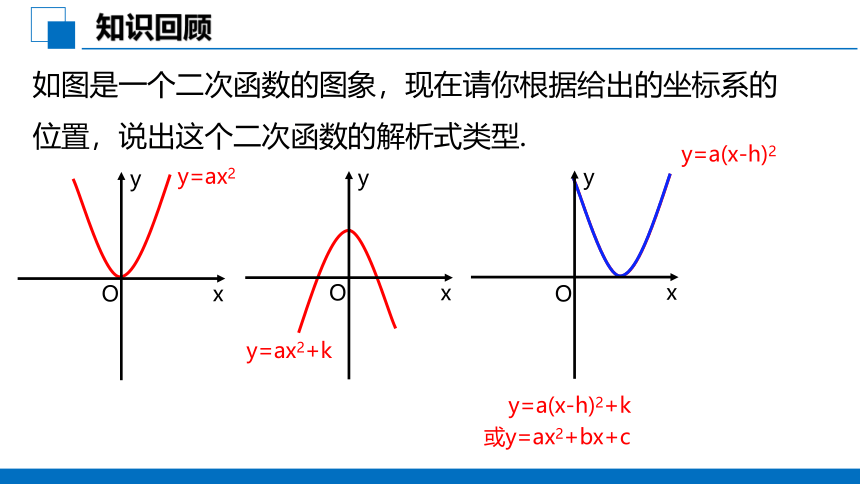
知识回顾
如图是一个二次函数的图象,现在请你根据给出的坐标系的位置,说出这个二次函数的解析式类型.
x
y
O
x
y
O
x
y
O
y=ax2
y=ax2+k
y=a(x-h)2
或y=ax2+bx+c
y=a(x-h)2+k
情境导入
生活中的抛物线
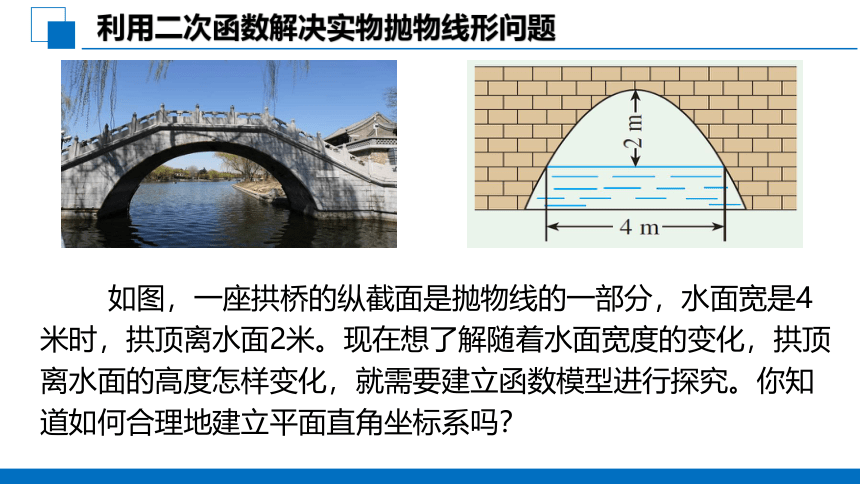
利用二次函数解决实物抛物线形问题
如图,一座拱桥的纵截面是抛物线的一部分,水面宽是4米时,拱顶离水面2米。现在想了解随着水面宽度的变化,拱顶离水面的高度怎样变化,就需要建立函数模型进行探究。你知道如何合理地建立平面直角坐标系吗?
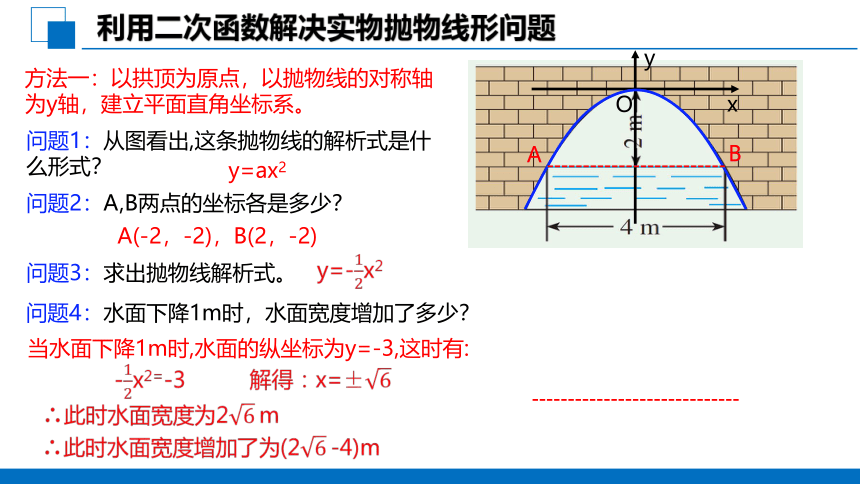
利用二次函数解决实物抛物线形问题
x
y
O
A
B
方法一:以拱顶为原点,以抛物线的对称轴为y轴,建立平面直角坐标系。
问题1:从图看出,这条抛物线的解析式是什么形式?
问题2:A,B两点的坐标各是多少?
y=ax2
A(-2,-2),B(2,-2)
问题3:求出抛物线解析式。
?
问题4:水面下降1m时,水面宽度增加了多少?
当水面下降1m时,水面的纵坐标为y=-3,这时有:
?
?
?
?
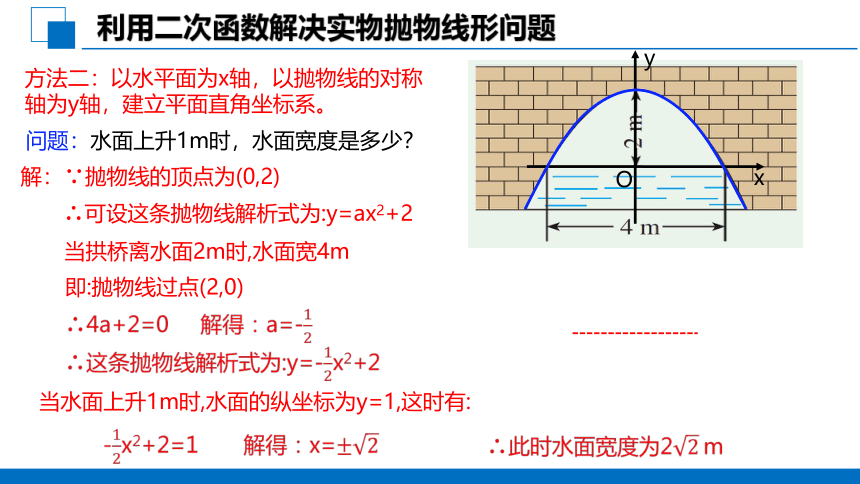
利用二次函数解决实物抛物线形问题
x
y
O
方法二:以水平面为x轴,以抛物线的对称轴为y轴,建立平面直角坐标系。
问题:水面上升1m时,水面宽度是多少?
当拱桥离水面2m时,水面宽4m
即:抛物线过点(2,0)
?
当水面上升1m时,水面的纵坐标为y=1,这时有:
∴可设这条抛物线解析式为:y=ax2+2
解:∵抛物线的顶点为(0,2)
?
?
?
利用二次函数解决实物抛物线形问题
x
y
O
方法三:以水平面为x轴,以抛物线和水面的一个交点为原点,建立平面直角坐标系。
x
y
O
问题:下面两图中的抛物线解析式各是多少?
?
?
知识要点
建立二次函数模型解决实际问题的基本步骤:
(1)、建立适当的直角系,并将已知条件转化为点的坐标;
(2)、合理地设出所求的函数的解析式;
(4)、利用二次函数的图象和性质解决实际问题。
(3)、并代入已知条件或点的坐标,求出关系式;
x
y
O
A
B
例题精讲
例:某公园要建造圆形喷水池,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.如果不计其它因素,那么水池的半径至少要多少m才能使喷出的水流不致落到池外?
O
A
建立函数模型
(1,2.25)
(0,1.25)
1
?
x
y
O
A
B
例题精讲
(1,2.25)
(0,1.25)
1
?
解:建立如图所示的坐标系,根据题意得:
A点坐标为(0,1.25),顶点坐标为(1,2.25).
∴如果不计其它因素,那么水池的半径至少
要2.5m,才能使喷出的水流不致落到池外。
令y=0,得:-(x-1)2+2.25=0
解得:x1=2.5
x2=-0.5(舍去)
∴点B的坐标为(2.5,0)
;
设抛物线解析式为y=a(x-1)2+2.25,
把A
(0,1.25)代入得:
a+2.25=1.25
解得:a=-1
抛物线表达式为:y=-(x-1)2+2.25.
针对训练
1.足球被从地面上踢起,它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在
s后落地.
4
?
x
y
O
2
课堂小结
转化
回归
(二次函数的图象和性质)
(实物中的抛物线形问题)
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标;
选择运算简便的方法.
实际问题
数学模型
转化的关键
课堂检测
1、有一座抛物线形拱桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m.如图所示的直角坐标系中,求出这条抛物线表示的函数的解析式;
O
A
C
D
B
y
x
20
m
解:设该拱桥形成的抛物线的解析式为y=ax2.
∵该抛物线过(10,-4),
∴-4=100a,a=-0.04
∴y=-0.04x2.
课堂检测
2.某公园草坪的防护栏是由100段形状相同的抛物线形组成的,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为(
)
A.50m
B.100m
C.160m
D.200m
C
课堂检测
3.悬索桥两端主塔塔顶之间的主悬钢索,其形状可近似地看作抛物线,水平桥面与主悬钢索之间用垂直钢索连接。已知两端主塔之间的水平距离为900m,两主塔塔顶距桥面的高度为81.5m,主悬钢索最低点离桥面的高度为0.5m。
(1)若以桥面所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,如图所示,求这条抛物线对应的函数表达式;
y
x
O
-450
450
(2)计算距离桥两端主塔分别为100m,50m处垂直钢索的长.
49.5m
64.5m
拓展训练
某工厂大门是一抛物线形的水泥建筑物,大门底部宽AB=4m,顶部C离地面的高度为4.4m,现有载满货物的汽车欲通过大门,货物顶部距地面2.7m,装货宽度为2.4m.这辆汽车能否顺利通过大门?若能,请你通过计算加以说明;若不能,请简要说明理由.
拓展训练
解:如图,以AB所在的直线为x轴,以AB的垂直平分线
为y轴,建立平面直角坐标系.
由题意可知:A(-2,0)
B(2,0)
C(0,4.4)
设抛物线解析式为y=ax2+4.4
∵抛物线过A(-2,0)
∴4a+4.4=0
解得:a=-1.1
∴抛物线解析式为y=-1.1x2+4.4
∴汽车能顺利经过大门.
?
第二十二章
二次函数
22.3
实际问题与二次函数
第3课时
拱桥问题和运动中的抛物线
灵宝市秦岭学校
九年级数学组
1
会建立二次函数模型,把实际问题转化为二次函数问题.(重点)
2
利用二次函数解决拱桥及运动中的有关问题.
(重、难点)
学习目标
知识回顾
如图是一个二次函数的图象,现在请你根据给出的坐标系的位置,说出这个二次函数的解析式类型.
x
y
O
x
y
O
x
y
O
y=ax2
y=ax2+k
y=a(x-h)2
或y=ax2+bx+c
y=a(x-h)2+k
情境导入
生活中的抛物线
利用二次函数解决实物抛物线形问题
如图,一座拱桥的纵截面是抛物线的一部分,水面宽是4米时,拱顶离水面2米。现在想了解随着水面宽度的变化,拱顶离水面的高度怎样变化,就需要建立函数模型进行探究。你知道如何合理地建立平面直角坐标系吗?
利用二次函数解决实物抛物线形问题
x
y
O
A
B
方法一:以拱顶为原点,以抛物线的对称轴为y轴,建立平面直角坐标系。
问题1:从图看出,这条抛物线的解析式是什么形式?
问题2:A,B两点的坐标各是多少?
y=ax2
A(-2,-2),B(2,-2)
问题3:求出抛物线解析式。
?
问题4:水面下降1m时,水面宽度增加了多少?
当水面下降1m时,水面的纵坐标为y=-3,这时有:
?
?
?
?
利用二次函数解决实物抛物线形问题
x
y
O
方法二:以水平面为x轴,以抛物线的对称轴为y轴,建立平面直角坐标系。
问题:水面上升1m时,水面宽度是多少?
当拱桥离水面2m时,水面宽4m
即:抛物线过点(2,0)
?
当水面上升1m时,水面的纵坐标为y=1,这时有:
∴可设这条抛物线解析式为:y=ax2+2
解:∵抛物线的顶点为(0,2)
?
?
?
利用二次函数解决实物抛物线形问题
x
y
O
方法三:以水平面为x轴,以抛物线和水面的一个交点为原点,建立平面直角坐标系。
x
y
O
问题:下面两图中的抛物线解析式各是多少?
?
?
知识要点
建立二次函数模型解决实际问题的基本步骤:
(1)、建立适当的直角系,并将已知条件转化为点的坐标;
(2)、合理地设出所求的函数的解析式;
(4)、利用二次函数的图象和性质解决实际问题。
(3)、并代入已知条件或点的坐标,求出关系式;
x
y
O
A
B
例题精讲
例:某公园要建造圆形喷水池,在水池中央垂直于水面处安装一个柱子OA,O恰在水面中心,OA=1.25m,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线落下,为使水流形状较为漂亮,要求设计成水流在离OA距离为1m处达到距水面最大高度2.25m.如果不计其它因素,那么水池的半径至少要多少m才能使喷出的水流不致落到池外?
O
A
建立函数模型
(1,2.25)
(0,1.25)
1
?
x
y
O
A
B
例题精讲
(1,2.25)
(0,1.25)
1
?
解:建立如图所示的坐标系,根据题意得:
A点坐标为(0,1.25),顶点坐标为(1,2.25).
∴如果不计其它因素,那么水池的半径至少
要2.5m,才能使喷出的水流不致落到池外。
令y=0,得:-(x-1)2+2.25=0
解得:x1=2.5
x2=-0.5(舍去)
∴点B的坐标为(2.5,0)
;
设抛物线解析式为y=a(x-1)2+2.25,
把A
(0,1.25)代入得:
a+2.25=1.25
解得:a=-1
抛物线表达式为:y=-(x-1)2+2.25.
针对训练
1.足球被从地面上踢起,它距地面的高度h(m)可用公式h=-4.9t2+19.6t来表示,其中t(s)表示足球被踢出后经过的时间,则球在
s后落地.
4
?
x
y
O
2
课堂小结
转化
回归
(二次函数的图象和性质)
(实物中的抛物线形问题)
建立恰当的直角坐标系
能够将实际距离准确的转化为点的坐标;
选择运算简便的方法.
实际问题
数学模型
转化的关键
课堂检测
1、有一座抛物线形拱桥,正常水位时桥下水面宽度为20m,拱顶距离水面4m.如图所示的直角坐标系中,求出这条抛物线表示的函数的解析式;
O
A
C
D
B
y
x
20
m
解:设该拱桥形成的抛物线的解析式为y=ax2.
∵该抛物线过(10,-4),
∴-4=100a,a=-0.04
∴y=-0.04x2.
课堂检测
2.某公园草坪的防护栏是由100段形状相同的抛物线形组成的,为了牢固起见,每段护栏需要间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图),则这条防护栏需要不锈钢支柱的总长度至少为(
)
A.50m
B.100m
C.160m
D.200m
C
课堂检测
3.悬索桥两端主塔塔顶之间的主悬钢索,其形状可近似地看作抛物线,水平桥面与主悬钢索之间用垂直钢索连接。已知两端主塔之间的水平距离为900m,两主塔塔顶距桥面的高度为81.5m,主悬钢索最低点离桥面的高度为0.5m。
(1)若以桥面所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,如图所示,求这条抛物线对应的函数表达式;
y
x
O
-450
450
(2)计算距离桥两端主塔分别为100m,50m处垂直钢索的长.
49.5m
64.5m
拓展训练
某工厂大门是一抛物线形的水泥建筑物,大门底部宽AB=4m,顶部C离地面的高度为4.4m,现有载满货物的汽车欲通过大门,货物顶部距地面2.7m,装货宽度为2.4m.这辆汽车能否顺利通过大门?若能,请你通过计算加以说明;若不能,请简要说明理由.
拓展训练
解:如图,以AB所在的直线为x轴,以AB的垂直平分线
为y轴,建立平面直角坐标系.
由题意可知:A(-2,0)
B(2,0)
C(0,4.4)
设抛物线解析式为y=ax2+4.4
∵抛物线过A(-2,0)
∴4a+4.4=0
解得:a=-1.1
∴抛物线解析式为y=-1.1x2+4.4
∴汽车能顺利经过大门.
?
同课章节目录
