人教版八年级数学上册第十三章13.1.2线段垂直平分线课件(共23张PPT)
文档属性
| 名称 | 人教版八年级数学上册第十三章13.1.2线段垂直平分线课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 684.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-19 16:32:44 | ||
图片预览



文档简介
(共23张PPT)
线段垂直平分线
106
国
道
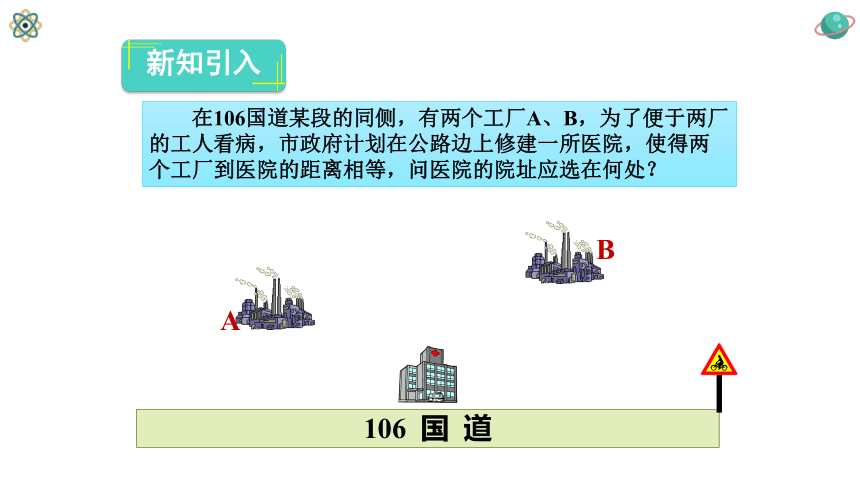
新知引入
A
B
在106国道某段的同侧,有两个工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂到医院的距离相等,问医院的院址应选在何处?
新知讲解
动手操作:直线MN垂直平分线段AB,垂足为C;在MN上任取点P
,
P1,
P2……,分别量一量点P
,
P1,
P2……到点A与点B的距离,你有什么发现?
由此你能得到什么规律?
P
M
N
C
A
B
P1
P2
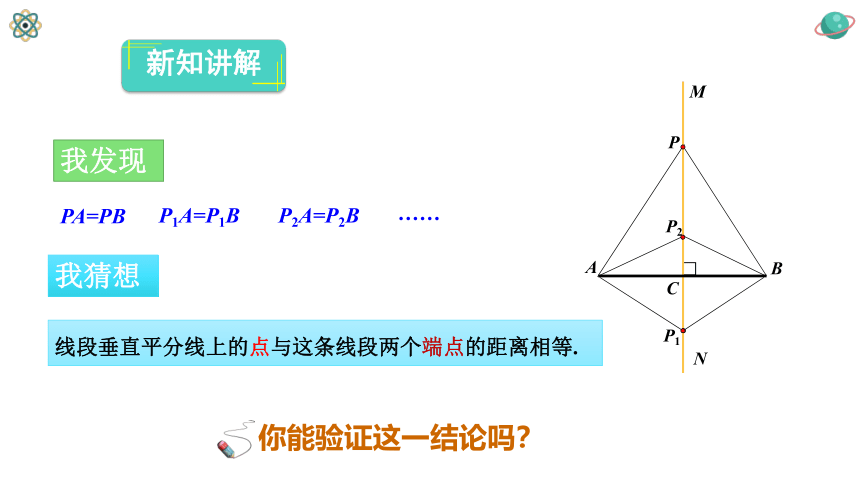
新知讲解
线段垂直平分线上的点与这条线段两个端点的距离相等.
我发现
PA=PB
P1A=P1B
……
P2A=P2B
你能验证这一结论吗?
P
M
N
C
A
B
P1
P2
我猜想
新知讲解
A
B
P
l
C
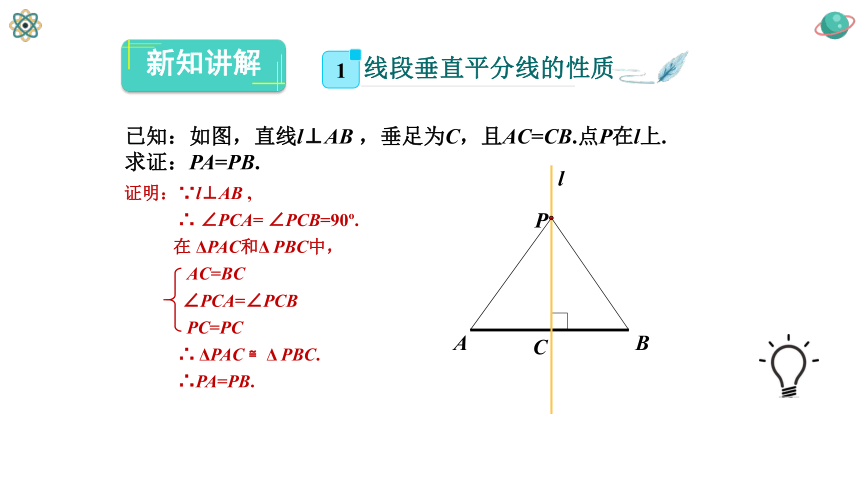
已知:如图,直线l⊥AB
,垂足为C,且AC=CB.点P在l上.
求证:PA=PB.
证明:∵l⊥AB
,
∴
∠PCA=
∠PCB=90?.
在
ΔPAC和Δ
PBC中,
AC=BC
∠PCA=∠PCB
PC=PC
∴
ΔPAC
≌Δ
PBC.
∴PA=PB.
线段垂直平分线的性质
1
新知讲解
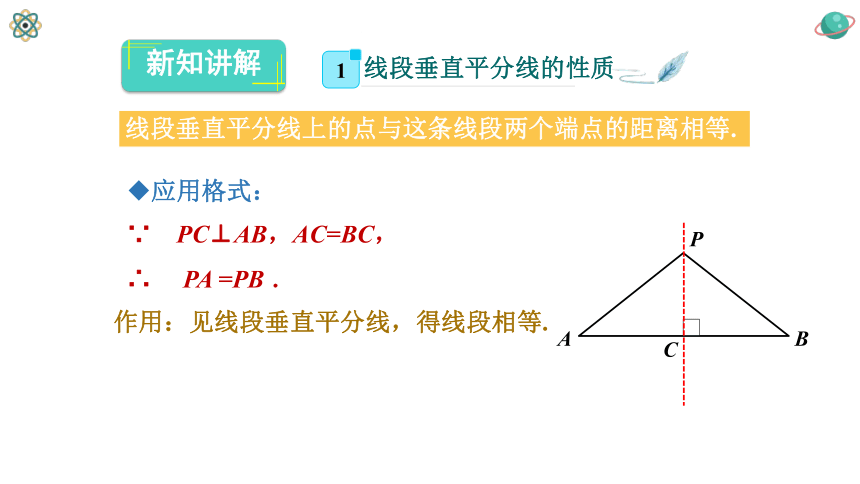
应用格式:
∵ PC⊥AB,AC=BC,
∴
PA
=PB
.
作用:见线段垂直平分线,得线段相等.
P
A
B
线段垂直平分线上的点与这条线段两个端点的距离相等.
C
线段垂直平分线的性质
1
新知应用
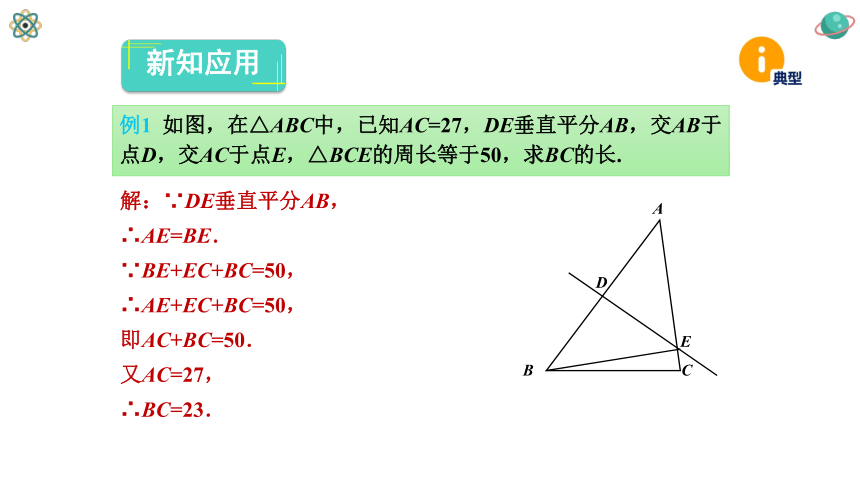
例1
如图,在△ABC中,已知AC=27,DE垂直平分AB,交AB于点D,交AC于点E,△BCE的周长等于50,求BC的长.
解:∵DE垂直平分AB,
∴AE=BE.
∵BE+EC+BC=50,
∴AE+EC+BC=50,
即AC+BC=50.
又AC=27,
∴BC=23.
A
B
C
D
E
新知应用
例2
如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于_______°.
A
B
C
D
E
解:∵在△ABC中,∠ABC=90°,∠C=20°,
∴∠BAC=180°-∠B-∠C=70°,
∵DE是边AC的垂直平分线,∠C=20°,
∴CE=AE,
∴∠EAC=∠C=20°,
∴∠BAE=∠BAC-∠EAC=70°-20°=50°.
50
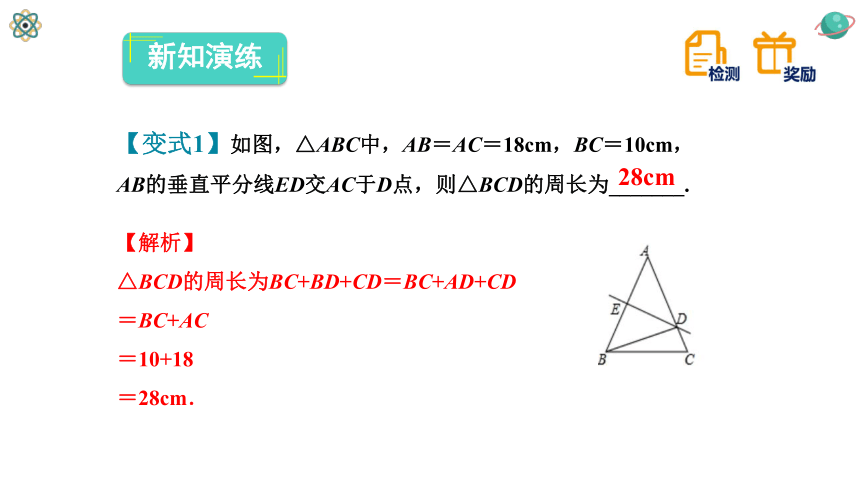
【变式1】如图,△ABC中,AB=AC=18cm,BC=10cm,AB的垂直平分线ED交AC于D点,则△BCD的周长为_______.
新知演练
28cm
【解析】
△BCD的周长为BC+BD+CD=BC+AD+CD
=BC+AC
=10+18
=28cm.
【变式2】如图,在△ABC中,∠C=90°,AB的垂直平分线MN分别交AC,AB于点D,E.
若∠CBD
:
∠DBA
=3:1,则∠A的度数为________.
新知演练
18°
提示:∠A=∠ABD=x,∠CBD=3x,5x=90°,x=18°.
新知引入
想一想:如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
P
A
B
合作探究
线段垂直平分线的判定
2
C
新知讲解
P
A
B
已知:如图,PA
=PB.
求证:点P
在线段AB
的垂直平分线上.
证明:过点P
作AB
的垂线PC,垂足为点C.
则∠PCA
=∠PCB
=90°.
在Rt△PCA
和Rt△PCB
中,
PA
=PB,PC
=PC,
∴
Rt△PCA
≌Rt△PCB(HL).
∴
AC
=BC.
又
PC⊥AB,
∴
点P
在线段AB
的垂直平分线上.
线段垂直平分线的判定
2
新知讲解
与线段两个端点距离相等的点在这条线段的垂直平分线上.
应用格式:
∵ PA
=PB,
∴ 点P
在AB
的垂直平分线上.
作用:判断一个点是否在线段的垂直平分线上.
P
A
B
新知讲解
你能再找一些到线段AB
两端点的距离相等的点吗?能找到多少个到线段AB
两端点距离相等的点?
这些点能组成什么图形?
P
A
B
C
l
与A,B
的距离相等的点都在直线l上,所以直线l
可以看成与A、B两点
的距离相等的所有点的集合.
新知应用
例3
如图,在四边形ABCD中,AB=AD,CB=CD,AC,BD交于点O.求证:AC⊥BD.
A
B
C
D
O
证明
:
∵AB=AD,
∴点A在线段BD的垂直平分线上.
∵CB=CD,
∴点C在线段BD的垂直平分线上.
∴AC是线段BD的垂直平分线,
∴AC⊥BD.
这是判断一条直线是线段的垂直平分线的方法.
新知应用
例4
已知:如图,在△ABC中,AB,BC的垂直平分线相交于点O,连接OA,OB,OC.
求证:点O在AC的垂直平分线上.
证明
:
∵点O在线段AB的垂直平分线上,
∴
OA=OB.
同理OB=OC.
∴
OA=OC.
∴
点O在AC的垂直平分线上.
结论:
三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等.
106
国
道
新知应用
A
B
在106国道某段的同侧,有两个工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂到医院的距离相等,问医院的院址应选在何处?
现在你能想到方法确定医院的位置了吗?
【变式1】在锐角三角形ABC内一点P,满足PA=PB=PC,则点P是△ABC
(
)
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
新知演练
D
【变式2】如图,在△ABC中,AD是高,在线段DC上取一点E,使BD=DE,已知AB+BD=DC,求证:E点在线段AC的垂直平分线上.
新知演练
证明:∵AD是高,∴AD⊥BC,
又∵BD=DE,
∴AD所在的直线是线段BE的垂直平分线,
∴AB=AE,
∴AB+BD=AE+DE,
又∵AB+BD=DC,
∴DC=AE+DE,
∴DE+EC=AE+DE
∴EC=AE,
∴点E在线段AC的垂直平分线上.
拓展提升
1.
如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.
解析:(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可得出△ADE≌△FCE,根据全等三角形的性质即可解答.
(2)先根据线段垂直平分线的性质得出出AB=BF,再结合(1)即可解答.
证明:(1)∵AD∥BC,∴∠ADC=∠ECF.
∵E是CD的中点,∴DE=EC.
又∵∠AED=∠CEF,
∴△ADE≌△FCE,
∴FC=AD.
(2)∵△ADE≌△FCE,
∴AE=EF,AD=CF.
∵BE⊥AE,∴BE是线段AF的垂直平分线,
∴AB=BF=BC+CF.
∵AD=CF,
∴AB=BC+AD.
拓展提升
2.如图所示,在△ABC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,试说明AD与EF的关系.
解:AD垂直平分EF.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴∠EAD=∠FAD,∠AED=∠AFD=90°.
又∵AD=AD,
∴△ADE≌△ADF,
∴AE=AF,DE=DF.
∴A、D均在线段EF的垂直平分线上,即直线AD垂直平分线段EF.
A
B
C
D
E
F
拓展提升
课堂总结
性质
判定
线段的垂直平分线的性质和判定
内容
内容
作用
线段的垂直平分线上的点到线段的两个端点的距离相等
作用
到线段的两个端点的距离相等的点在线段的垂直平分线上
见垂直平分线,得线段相等
判断一个点是否在线段的垂直平分线上
线段垂直平分线
106
国
道
新知引入
A
B
在106国道某段的同侧,有两个工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂到医院的距离相等,问医院的院址应选在何处?
新知讲解
动手操作:直线MN垂直平分线段AB,垂足为C;在MN上任取点P
,
P1,
P2……,分别量一量点P
,
P1,
P2……到点A与点B的距离,你有什么发现?
由此你能得到什么规律?
P
M
N
C
A
B
P1
P2
新知讲解
线段垂直平分线上的点与这条线段两个端点的距离相等.
我发现
PA=PB
P1A=P1B
……
P2A=P2B
你能验证这一结论吗?
P
M
N
C
A
B
P1
P2
我猜想
新知讲解
A
B
P
l
C
已知:如图,直线l⊥AB
,垂足为C,且AC=CB.点P在l上.
求证:PA=PB.
证明:∵l⊥AB
,
∴
∠PCA=
∠PCB=90?.
在
ΔPAC和Δ
PBC中,
AC=BC
∠PCA=∠PCB
PC=PC
∴
ΔPAC
≌Δ
PBC.
∴PA=PB.
线段垂直平分线的性质
1
新知讲解
应用格式:
∵ PC⊥AB,AC=BC,
∴
PA
=PB
.
作用:见线段垂直平分线,得线段相等.
P
A
B
线段垂直平分线上的点与这条线段两个端点的距离相等.
C
线段垂直平分线的性质
1
新知应用
例1
如图,在△ABC中,已知AC=27,DE垂直平分AB,交AB于点D,交AC于点E,△BCE的周长等于50,求BC的长.
解:∵DE垂直平分AB,
∴AE=BE.
∵BE+EC+BC=50,
∴AE+EC+BC=50,
即AC+BC=50.
又AC=27,
∴BC=23.
A
B
C
D
E
新知应用
例2
如图,在△ABC中,∠ABC=90°,∠C=20°,DE是边AC的垂直平分线,连结AE,则∠BAE等于_______°.
A
B
C
D
E
解:∵在△ABC中,∠ABC=90°,∠C=20°,
∴∠BAC=180°-∠B-∠C=70°,
∵DE是边AC的垂直平分线,∠C=20°,
∴CE=AE,
∴∠EAC=∠C=20°,
∴∠BAE=∠BAC-∠EAC=70°-20°=50°.
50
【变式1】如图,△ABC中,AB=AC=18cm,BC=10cm,AB的垂直平分线ED交AC于D点,则△BCD的周长为_______.
新知演练
28cm
【解析】
△BCD的周长为BC+BD+CD=BC+AD+CD
=BC+AC
=10+18
=28cm.
【变式2】如图,在△ABC中,∠C=90°,AB的垂直平分线MN分别交AC,AB于点D,E.
若∠CBD
:
∠DBA
=3:1,则∠A的度数为________.
新知演练
18°
提示:∠A=∠ABD=x,∠CBD=3x,5x=90°,x=18°.
新知引入
想一想:如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
P
A
B
合作探究
线段垂直平分线的判定
2
C
新知讲解
P
A
B
已知:如图,PA
=PB.
求证:点P
在线段AB
的垂直平分线上.
证明:过点P
作AB
的垂线PC,垂足为点C.
则∠PCA
=∠PCB
=90°.
在Rt△PCA
和Rt△PCB
中,
PA
=PB,PC
=PC,
∴
Rt△PCA
≌Rt△PCB(HL).
∴
AC
=BC.
又
PC⊥AB,
∴
点P
在线段AB
的垂直平分线上.
线段垂直平分线的判定
2
新知讲解
与线段两个端点距离相等的点在这条线段的垂直平分线上.
应用格式:
∵ PA
=PB,
∴ 点P
在AB
的垂直平分线上.
作用:判断一个点是否在线段的垂直平分线上.
P
A
B
新知讲解
你能再找一些到线段AB
两端点的距离相等的点吗?能找到多少个到线段AB
两端点距离相等的点?
这些点能组成什么图形?
P
A
B
C
l
与A,B
的距离相等的点都在直线l上,所以直线l
可以看成与A、B两点
的距离相等的所有点的集合.
新知应用
例3
如图,在四边形ABCD中,AB=AD,CB=CD,AC,BD交于点O.求证:AC⊥BD.
A
B
C
D
O
证明
:
∵AB=AD,
∴点A在线段BD的垂直平分线上.
∵CB=CD,
∴点C在线段BD的垂直平分线上.
∴AC是线段BD的垂直平分线,
∴AC⊥BD.
这是判断一条直线是线段的垂直平分线的方法.
新知应用
例4
已知:如图,在△ABC中,AB,BC的垂直平分线相交于点O,连接OA,OB,OC.
求证:点O在AC的垂直平分线上.
证明
:
∵点O在线段AB的垂直平分线上,
∴
OA=OB.
同理OB=OC.
∴
OA=OC.
∴
点O在AC的垂直平分线上.
结论:
三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等.
106
国
道
新知应用
A
B
在106国道某段的同侧,有两个工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得两个工厂到医院的距离相等,问医院的院址应选在何处?
现在你能想到方法确定医院的位置了吗?
【变式1】在锐角三角形ABC内一点P,满足PA=PB=PC,则点P是△ABC
(
)
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
新知演练
D
【变式2】如图,在△ABC中,AD是高,在线段DC上取一点E,使BD=DE,已知AB+BD=DC,求证:E点在线段AC的垂直平分线上.
新知演练
证明:∵AD是高,∴AD⊥BC,
又∵BD=DE,
∴AD所在的直线是线段BE的垂直平分线,
∴AB=AE,
∴AB+BD=AE+DE,
又∵AB+BD=DC,
∴DC=AE+DE,
∴DE+EC=AE+DE
∴EC=AE,
∴点E在线段AC的垂直平分线上.
拓展提升
1.
如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)FC=AD;(2)AB=BC+AD.
解析:(1)根据AD∥BC可知∠ADC=∠ECF,再根据E是CD的中点可得出△ADE≌△FCE,根据全等三角形的性质即可解答.
(2)先根据线段垂直平分线的性质得出出AB=BF,再结合(1)即可解答.
证明:(1)∵AD∥BC,∴∠ADC=∠ECF.
∵E是CD的中点,∴DE=EC.
又∵∠AED=∠CEF,
∴△ADE≌△FCE,
∴FC=AD.
(2)∵△ADE≌△FCE,
∴AE=EF,AD=CF.
∵BE⊥AE,∴BE是线段AF的垂直平分线,
∴AB=BF=BC+CF.
∵AD=CF,
∴AB=BC+AD.
拓展提升
2.如图所示,在△ABC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,试说明AD与EF的关系.
解:AD垂直平分EF.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴∠EAD=∠FAD,∠AED=∠AFD=90°.
又∵AD=AD,
∴△ADE≌△ADF,
∴AE=AF,DE=DF.
∴A、D均在线段EF的垂直平分线上,即直线AD垂直平分线段EF.
A
B
C
D
E
F
拓展提升
课堂总结
性质
判定
线段的垂直平分线的性质和判定
内容
内容
作用
线段的垂直平分线上的点到线段的两个端点的距离相等
作用
到线段的两个端点的距离相等的点在线段的垂直平分线上
见垂直平分线,得线段相等
判断一个点是否在线段的垂直平分线上
