人教版数学八年级上册 第十二章全等三角形综合训练(word版,无答案)
文档属性
| 名称 | 人教版数学八年级上册 第十二章全等三角形综合训练(word版,无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 69.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-18 12:17:01 | ||
图片预览



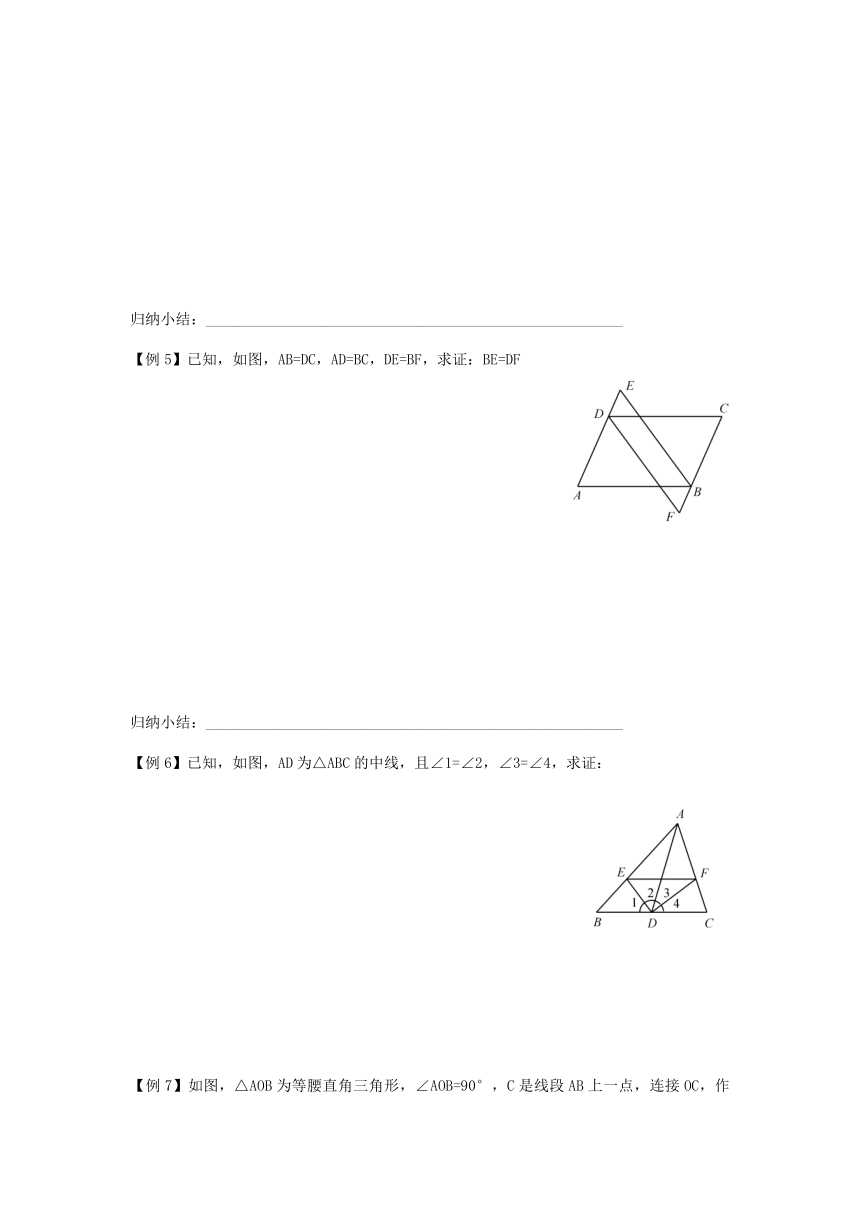
文档简介
全等三角形综合训练
一、知识要点
全等三角形是平面几何内容的基础,这是因为全等三角形是研究特殊三角形、四边形等图形性质的有力工具,是解决与线段、角相关问题的一个出发点,运用全等三角形,可以证明线段相等、线段和差倍分、角相等、两直线位置关系等常见的几何问题.
利用全等三角形证明问题,关键在于从复杂图形中找到一对基础的三角形,这对基础的三角形从实质上来说,是由三角形全等判定定理中的一对三角形变换而来,也可能是由几对三角形组成,期间的关系互相传递,应熟悉涉及公共边、公共角的基本图形.
(1)全等三角形的概念及其性质,注意:平移、翻折、旋转前后的两个图形全等;
(2)全等三角形的判定方法:SSS、SAS、ASA、AAS、HL,注意:SSA、AAA
全等
二、基础能力测试:
1.全等三角形是两个能够______的图形,全等图形的____和_____都相同.
2.如图,把△ABC沿着直线BC为轴翻转180°后变到△DBC的位置,那么△ABC与△DBC____
全等图形(填“是”或“不是”);若△ABC的面积是3,则△DBC的面积为_______.
3.如图,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点处,则BE的长为_________.
4.如图,已知△ABC≌△DEF,且AB=4,BC=5,AC=6,则DF的长为_______.
5.如图,在△ABC中,点D、E分别是边AC、BC上的点,若△ADB≌△EDC,则∠C的度数为________.
6.如图,△ABC≌△ADE,BC的延长线交DA于点F,交DE于点G,已知∠ACB=∠AED=105°,∠B=∠D=25°,求∠DFB和∠DGB的度数.
【例1】已知如图,点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF.
求证:∠A=∠D
归纳小结:_______________________________________________________
【例2】已知如图,点A、B、C、D在同一条直线上,AC=BD,AE⊥AB,CD⊥DF,AE=DF.
求证:∠E=∠F
归纳小结:_______________________________________________________
【例3】已知,如图,等腰△ABC和等腰△ADE中,AB=AC,AD=AE,且∠CAB=∠EAD.
求证:CE=BD
归纳小结:_______________________________________________________
【例4】如图,△ABC中,分别以AB、AC为腰,以点A为顶角顶点作等腰△ABM,等腰△CAN,且∠CAN=∠ABM
(1)如图1,求证:BC=MN;
(2)如图2,若MN⊥BC,求证:AB⊥AM
归纳小结:_______________________________________________________
【例5】已知,如图,AB=DC,AD=BC,DE=BF,求证:BE=DF
归纳小结:_______________________________________________________
【例6】已知,如图,AD为△ABC的中线,且∠1=∠2,∠3=∠4,求证:
【例7】如图,△AOB为等腰直角三角形,∠AOB=90°,C是线段AB上一点,连接OC,作OG⊥OC,且OG=OC,连接AG,取CF=FB,连OF交AG于H点,求证:OH⊥AG
归纳小结:_______________________________________________________
四、反馈练习
1.如图,已知BC=DE,BE=DC.
求证:(1)BC∥DE;(2)∠A=∠ADE
小明是这样想的,请你给小明的每个想法填上依据.
连接BD,在△BCD和△DEB中,
△BCD≌△DEB(_____________)
∠CBD=∠EDB(_____________)
BC∥DE
(_____________)
∠A=∠ADE
(_____________)
2.已知,如图,AB=DC,AC=BD,求证:∠A=∠D
3.如图,AC与BD交于点O,AD=CB,点E、F是BD上两点,且AE=CF,DE=BF,请推导下列结论:
(1)∠D=∠B;(2)AE∥CF
4.已知,如图,AE=CF,AD∥BC,AD=CB,求证:△ADF≌△CBE
5.如图,已知AB=AD,∠1=∠2,AC=AE,求证:DE=BC,∠1=∠CDE
6.如图,B、D、C在一条直线上,AB=BC,BD=EC,AB⊥BC,EC⊥BC,求证:AF⊥BE
7.已知,如图,AB=AC,AD=AE,AB、DC相交于点M,AC、BE相交于点N,∠DAB=∠EAC.
求证:CD=BE
8.如图,在△ABC外有Rt△ABD和Rt△ACE,∠DAB=∠EAC=90°,AD=AB,AC=AE,CD与BE交于M点,求证:DC=BE,DC⊥BE
9.已知,如图,D为BC中点,DE⊥DF,E、F分别在AB、AC上.
求证:
10.如图,已知:AD是△ABC的中线,AE⊥AC,AF⊥AB,且AE=AC,AF=AB.求证:
一、知识要点
全等三角形是平面几何内容的基础,这是因为全等三角形是研究特殊三角形、四边形等图形性质的有力工具,是解决与线段、角相关问题的一个出发点,运用全等三角形,可以证明线段相等、线段和差倍分、角相等、两直线位置关系等常见的几何问题.
利用全等三角形证明问题,关键在于从复杂图形中找到一对基础的三角形,这对基础的三角形从实质上来说,是由三角形全等判定定理中的一对三角形变换而来,也可能是由几对三角形组成,期间的关系互相传递,应熟悉涉及公共边、公共角的基本图形.
(1)全等三角形的概念及其性质,注意:平移、翻折、旋转前后的两个图形全等;
(2)全等三角形的判定方法:SSS、SAS、ASA、AAS、HL,注意:SSA、AAA
全等
二、基础能力测试:
1.全等三角形是两个能够______的图形,全等图形的____和_____都相同.
2.如图,把△ABC沿着直线BC为轴翻转180°后变到△DBC的位置,那么△ABC与△DBC____
全等图形(填“是”或“不是”);若△ABC的面积是3,则△DBC的面积为_______.
3.如图,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,点E在BC上,将△ABC沿AE折叠,使点B落在AC边上的点处,则BE的长为_________.
4.如图,已知△ABC≌△DEF,且AB=4,BC=5,AC=6,则DF的长为_______.
5.如图,在△ABC中,点D、E分别是边AC、BC上的点,若△ADB≌△EDC,则∠C的度数为________.
6.如图,△ABC≌△ADE,BC的延长线交DA于点F,交DE于点G,已知∠ACB=∠AED=105°,∠B=∠D=25°,求∠DFB和∠DGB的度数.
【例1】已知如图,点B、E、C、F在同一条直线上,AB=DE,AC=DF,BE=CF.
求证:∠A=∠D
归纳小结:_______________________________________________________
【例2】已知如图,点A、B、C、D在同一条直线上,AC=BD,AE⊥AB,CD⊥DF,AE=DF.
求证:∠E=∠F
归纳小结:_______________________________________________________
【例3】已知,如图,等腰△ABC和等腰△ADE中,AB=AC,AD=AE,且∠CAB=∠EAD.
求证:CE=BD
归纳小结:_______________________________________________________
【例4】如图,△ABC中,分别以AB、AC为腰,以点A为顶角顶点作等腰△ABM,等腰△CAN,且∠CAN=∠ABM
(1)如图1,求证:BC=MN;
(2)如图2,若MN⊥BC,求证:AB⊥AM
归纳小结:_______________________________________________________
【例5】已知,如图,AB=DC,AD=BC,DE=BF,求证:BE=DF
归纳小结:_______________________________________________________
【例6】已知,如图,AD为△ABC的中线,且∠1=∠2,∠3=∠4,求证:
【例7】如图,△AOB为等腰直角三角形,∠AOB=90°,C是线段AB上一点,连接OC,作OG⊥OC,且OG=OC,连接AG,取CF=FB,连OF交AG于H点,求证:OH⊥AG
归纳小结:_______________________________________________________
四、反馈练习
1.如图,已知BC=DE,BE=DC.
求证:(1)BC∥DE;(2)∠A=∠ADE
小明是这样想的,请你给小明的每个想法填上依据.
连接BD,在△BCD和△DEB中,
△BCD≌△DEB(_____________)
∠CBD=∠EDB(_____________)
BC∥DE
(_____________)
∠A=∠ADE
(_____________)
2.已知,如图,AB=DC,AC=BD,求证:∠A=∠D
3.如图,AC与BD交于点O,AD=CB,点E、F是BD上两点,且AE=CF,DE=BF,请推导下列结论:
(1)∠D=∠B;(2)AE∥CF
4.已知,如图,AE=CF,AD∥BC,AD=CB,求证:△ADF≌△CBE
5.如图,已知AB=AD,∠1=∠2,AC=AE,求证:DE=BC,∠1=∠CDE
6.如图,B、D、C在一条直线上,AB=BC,BD=EC,AB⊥BC,EC⊥BC,求证:AF⊥BE
7.已知,如图,AB=AC,AD=AE,AB、DC相交于点M,AC、BE相交于点N,∠DAB=∠EAC.
求证:CD=BE
8.如图,在△ABC外有Rt△ABD和Rt△ACE,∠DAB=∠EAC=90°,AD=AB,AC=AE,CD与BE交于M点,求证:DC=BE,DC⊥BE
9.已知,如图,D为BC中点,DE⊥DF,E、F分别在AB、AC上.
求证:
10.如图,已知:AD是△ABC的中线,AE⊥AC,AF⊥AB,且AE=AC,AF=AB.求证:
