五年级上册数学课件掷一掷人教版(共31张PPT)
文档属性
| 名称 | 五年级上册数学课件掷一掷人教版(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 837.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-19 00:00:00 | ||
图片预览










文档简介
★掷一掷
猜一猜
四四方方麻子眼,猜猜它有几个点。
(打一娱乐工具)
游戏规则:
1.游戏分为A、B两队。
2.如果掷出4,A队赢。掷出1.2.3.5.6,B队赢。
玩一玩(一)
学习目标:
1.通过活动,会综合运用已学过的组合、统计、可能性、找规律等有关知识,探讨事件发生的可能性的大小。
2.经历观察、猜想、试验、验证的学习过程,培养学生提出问题,分析和解决问题的能力,以及合作交流的能力。
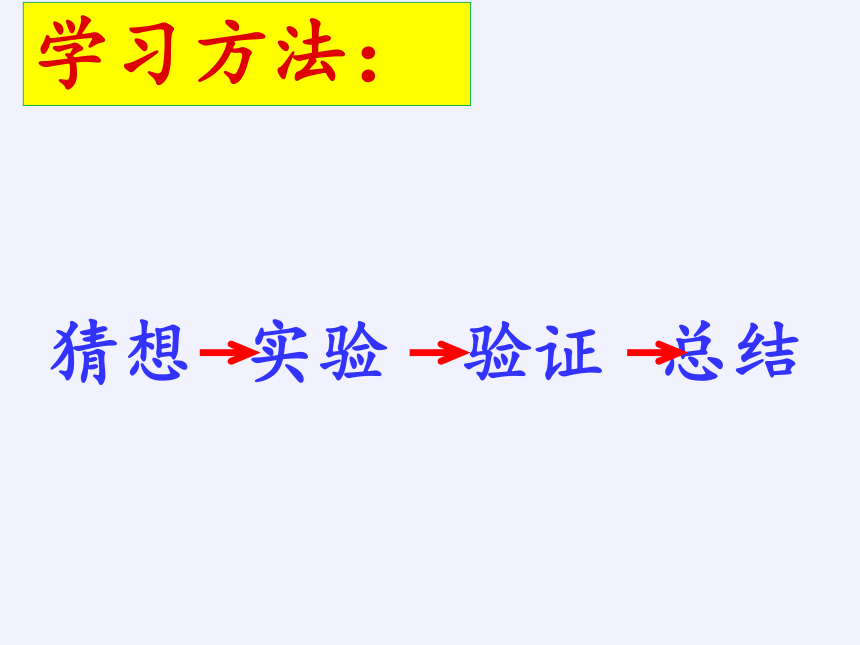
学习方法:
猜想 实验 验证 总结
游戏规则:
1.游戏分为A、B两队。
2.掷20次,如果掷出和是5.6.7.8.9,A队赢。掷出2.3.4.10.11.12,B队赢。
玩一玩(二)
组长:用画“正”法记录A队赢还是B队赢。
赢的次数(用画“正”法记录)
合 计
A队
(5、6、7、8、9)
次
B 队
(2、3、4、10、11、12)
次
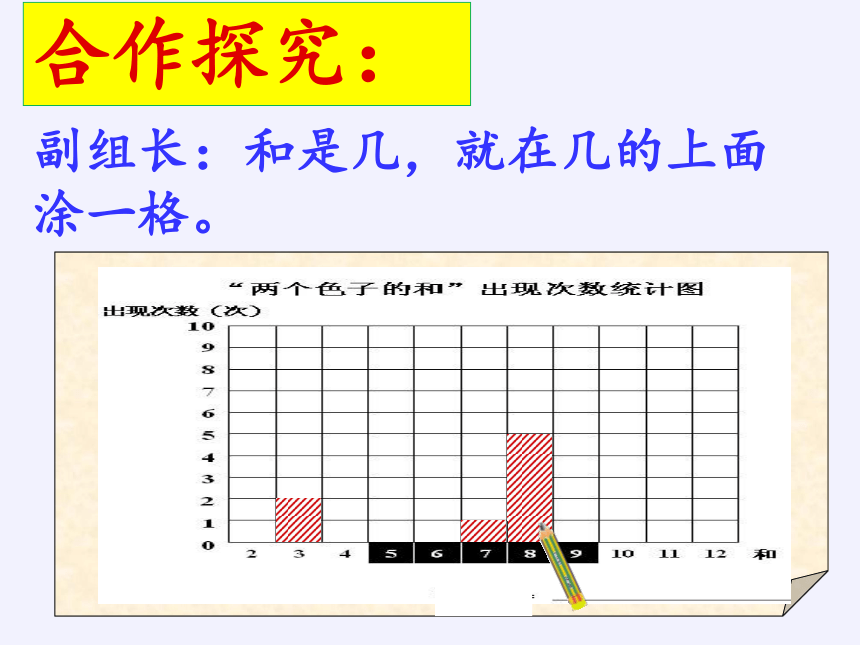
合作探究:
副组长:和是几,就在几的上面涂一格。
合作探究:
合作探究:
剩下同学计算每次掷的和,配合组长和副组长。
游戏规则:
1.游戏分为A、B两队。
2.掷20次,如果掷出和是5.6.7.8.9,A队赢。掷出2.3.4.10.11.12,B队赢。
玩一玩(二)
*组长:继续画“正”法记录A队赢还是B队赢。
玩一玩(三)
*副组长:继续和是几,就在几的上面涂一格。涂满其中任意一列,活动结束。
*剩下同学轮流掷,继续计算每次掷的和,配合组长和副组长。
“和”的种类少的反而出现可能性的大,“和”的种类多的反而出现可能性的小,
想一想
探究规律:
小组合作应用列表、画图、计算等不同的形式探究规律。
2
5
6
7
8
9
10
11
12
3
4
1
5
6
6
6
6
4
1
5
1
6
2
6
3
6
2
1
3
1
4
1
1
4
2
4
3
5
3
6
3
4
1
4
6
3
3
3
4
4
4
5
4
3
1
3
2
5
1
5
2
6
2
6
1
6
5
5
5
2
4
2
5
3
5
4
5
1
2
2
2
3
2
色子1
色子2
和
2
1
1
3
1
2
2
1
4
1
3
2
2
3
1
5
1
4
2
3
3
2
4
1
6
1
5
2
4
3
3
4
2
5
1
7
1
6
2
5
3
4
4
3
5
2
6
1
色子1
色子2
和
8
2
6
3
5
4
4
5
3
6
2
3
6
5
4
4
5
6
3
9
10
4
6
5
5
6
4
5
6
6
5
11
6
6
12
+
1
2
3
4
5
6
1
2
3
4
5
6
2
3
4
7
5
6
3
4
5
6
7
8
4
5
5
6
6
6
7
7
7
7
8
8
8
8
9
9
9
9
10
10
10
11
11
12
实验1000次“两个色子的和”出现情况统计图
2 3 4 5 6 7 8 9 10 11 12
5
10
15
20
25
30
35
40
45
50
60
65
55
70
75
80
85
90
95
100
105
115
120
110
次数
125
“和”的次数出现多的可能性大,“和”的次数出现少的可能性小。
辨一辨
天虹商场店庆活动,可以掷两颗骰子,根据两颗骰子的总点数决定送礼券多少。下面是商场销售经理所设计的两种促销方案:
总点数
2
3
4
5
6
7
8
9
10
11
12
金额/元
20
40
60
80
100
120
100
80
60
40
20
方案A:
方案B:
总点数
2
3
4
5
6
7
8
9
10
11
12
金额/元
120
100
80
60
40
20
40
60
80
100
120
选一选
*如果你是商场董事长,你会采取哪种方案?
方案A:
方案B:
总点数
2
3
4
5
6
7
8
9
10
11
12
金额/元
120
100
80
60
40
20
40
60
80
100
120
选一选
*如果你是顾客,你希望商场选择哪种方案?
总点数
2
3
4
5
6
7
8
9
10
11
12
金额/元
20
40
60
80
100
120
100
80
60
40
20
等 级
奖 品
两球之和
幸运奖
手机1部
1,13
1
2
5
4
3
6
1
2
5
4
3
6
好消息
凡在本商场购物满880元的顾客,可到抽奖箱抽两个数字球,根据两个球上数字的和领取相应的奖品。
参与奖
矿泉水1瓶
2,12
小芳做套圈的游戏,她套中2个数,加起来等于12.她套中的可能是哪两个数?
套一套
4
7
9
10
8
3
有3张数字卡片 ,任意抽两张,将卡片上的数字相乘,积是双数的男生赢,否则女生赢。这个游戏公平吗?
3
2
5
算一算
同时掷3个色子,
(1)掷出来的点数之和是2。( )
(2)掷出来的点数之和是8。( )
(3)掷出来的点数是18。 ( )
一定 不可能 可能
选一选
谈一谈
本节课你有什么收获?
延伸拓展:
1.同时掷2个色子,计算出朝上面的2个数的差。你能发现哪些差出现得多?哪些差出现得少?
2.同时掷3个色子,计算出朝上面的3个数的和。你能发现哪些和出现得多?哪些和出现得少?
课外延伸:
概率论是研究随机性或不确定性等现象的数学。典型的随机实验有掷色子、扔硬币、抽扑克以及轮盘游戏等。在大学会学到概率论,掌握概率对生活有很大的帮助。
请多指导,谢谢光临!
谢 谢
猜一猜
四四方方麻子眼,猜猜它有几个点。
(打一娱乐工具)
游戏规则:
1.游戏分为A、B两队。
2.如果掷出4,A队赢。掷出1.2.3.5.6,B队赢。
玩一玩(一)
学习目标:
1.通过活动,会综合运用已学过的组合、统计、可能性、找规律等有关知识,探讨事件发生的可能性的大小。
2.经历观察、猜想、试验、验证的学习过程,培养学生提出问题,分析和解决问题的能力,以及合作交流的能力。
学习方法:
猜想 实验 验证 总结
游戏规则:
1.游戏分为A、B两队。
2.掷20次,如果掷出和是5.6.7.8.9,A队赢。掷出2.3.4.10.11.12,B队赢。
玩一玩(二)
组长:用画“正”法记录A队赢还是B队赢。
赢的次数(用画“正”法记录)
合 计
A队
(5、6、7、8、9)
次
B 队
(2、3、4、10、11、12)
次
合作探究:
副组长:和是几,就在几的上面涂一格。
合作探究:
合作探究:
剩下同学计算每次掷的和,配合组长和副组长。
游戏规则:
1.游戏分为A、B两队。
2.掷20次,如果掷出和是5.6.7.8.9,A队赢。掷出2.3.4.10.11.12,B队赢。
玩一玩(二)
*组长:继续画“正”法记录A队赢还是B队赢。
玩一玩(三)
*副组长:继续和是几,就在几的上面涂一格。涂满其中任意一列,活动结束。
*剩下同学轮流掷,继续计算每次掷的和,配合组长和副组长。
“和”的种类少的反而出现可能性的大,“和”的种类多的反而出现可能性的小,
想一想
探究规律:
小组合作应用列表、画图、计算等不同的形式探究规律。
2
5
6
7
8
9
10
11
12
3
4
1
5
6
6
6
6
4
1
5
1
6
2
6
3
6
2
1
3
1
4
1
1
4
2
4
3
5
3
6
3
4
1
4
6
3
3
3
4
4
4
5
4
3
1
3
2
5
1
5
2
6
2
6
1
6
5
5
5
2
4
2
5
3
5
4
5
1
2
2
2
3
2
色子1
色子2
和
2
1
1
3
1
2
2
1
4
1
3
2
2
3
1
5
1
4
2
3
3
2
4
1
6
1
5
2
4
3
3
4
2
5
1
7
1
6
2
5
3
4
4
3
5
2
6
1
色子1
色子2
和
8
2
6
3
5
4
4
5
3
6
2
3
6
5
4
4
5
6
3
9
10
4
6
5
5
6
4
5
6
6
5
11
6
6
12
+
1
2
3
4
5
6
1
2
3
4
5
6
2
3
4
7
5
6
3
4
5
6
7
8
4
5
5
6
6
6
7
7
7
7
8
8
8
8
9
9
9
9
10
10
10
11
11
12
实验1000次“两个色子的和”出现情况统计图
2 3 4 5 6 7 8 9 10 11 12
5
10
15
20
25
30
35
40
45
50
60
65
55
70
75
80
85
90
95
100
105
115
120
110
次数
125
“和”的次数出现多的可能性大,“和”的次数出现少的可能性小。
辨一辨
天虹商场店庆活动,可以掷两颗骰子,根据两颗骰子的总点数决定送礼券多少。下面是商场销售经理所设计的两种促销方案:
总点数
2
3
4
5
6
7
8
9
10
11
12
金额/元
20
40
60
80
100
120
100
80
60
40
20
方案A:
方案B:
总点数
2
3
4
5
6
7
8
9
10
11
12
金额/元
120
100
80
60
40
20
40
60
80
100
120
选一选
*如果你是商场董事长,你会采取哪种方案?
方案A:
方案B:
总点数
2
3
4
5
6
7
8
9
10
11
12
金额/元
120
100
80
60
40
20
40
60
80
100
120
选一选
*如果你是顾客,你希望商场选择哪种方案?
总点数
2
3
4
5
6
7
8
9
10
11
12
金额/元
20
40
60
80
100
120
100
80
60
40
20
等 级
奖 品
两球之和
幸运奖
手机1部
1,13
1
2
5
4
3
6
1
2
5
4
3
6
好消息
凡在本商场购物满880元的顾客,可到抽奖箱抽两个数字球,根据两个球上数字的和领取相应的奖品。
参与奖
矿泉水1瓶
2,12
小芳做套圈的游戏,她套中2个数,加起来等于12.她套中的可能是哪两个数?
套一套
4
7
9
10
8
3
有3张数字卡片 ,任意抽两张,将卡片上的数字相乘,积是双数的男生赢,否则女生赢。这个游戏公平吗?
3
2
5
算一算
同时掷3个色子,
(1)掷出来的点数之和是2。( )
(2)掷出来的点数之和是8。( )
(3)掷出来的点数是18。 ( )
一定 不可能 可能
选一选
谈一谈
本节课你有什么收获?
延伸拓展:
1.同时掷2个色子,计算出朝上面的2个数的差。你能发现哪些差出现得多?哪些差出现得少?
2.同时掷3个色子,计算出朝上面的3个数的和。你能发现哪些和出现得多?哪些和出现得少?
课外延伸:
概率论是研究随机性或不确定性等现象的数学。典型的随机实验有掷色子、扔硬币、抽扑克以及轮盘游戏等。在大学会学到概率论,掌握概率对生活有很大的帮助。
请多指导,谢谢光临!
谢 谢
