2019-2020学年湖北省鄂州一中九年级下学期开学数学试卷 (解析版)
文档属性
| 名称 | 2019-2020学年湖北省鄂州一中九年级下学期开学数学试卷 (解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-19 00:00:00 | ||
图片预览


文档简介
2019-2020学年湖北省鄂州一中九年级第二学期开学数学试卷
一、选择题(共10小题).
1.(3分)一个数的相反数是﹣2020,则这个数是( )
A.2020 B.﹣2020 C. D.
2.(3分)2019年9月30日上映的电影《我和我的祖国》掀起一股观影热潮,截止12月25日票房累计达3150000000元,3150000000用科学记数法表示正确的是( )
A.315×107 B.3.15×1010 C.3.15×109 D.0.315×1010
3.(3分)下列运算正确的是( )
A.2x2?3x2=6x2 B.x3+x5=x8
C.x4÷x=x3 D.(x5)2=x7
4.(3分)如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图,若组成这个几何体的小正方体的个数为n,则n的最大值为( )
A.9 B.10 C.12 D.14
5.(3分)已知直线m∥n,将一块含30°角的直角三角板按如图所示方式放置(∠ABC=30°),并且顶点A,C分别落在直线m,n上,若∠1=38°,则∠2的度数是( )
A.20° B.22° C.28° D.38°
6.(3分)一组数据6,7,9,9,9,0,3,若去掉一个数据9,则下列统计量不发生变化的是( )
A.平均数 B.众数 C.中位数 D.方差
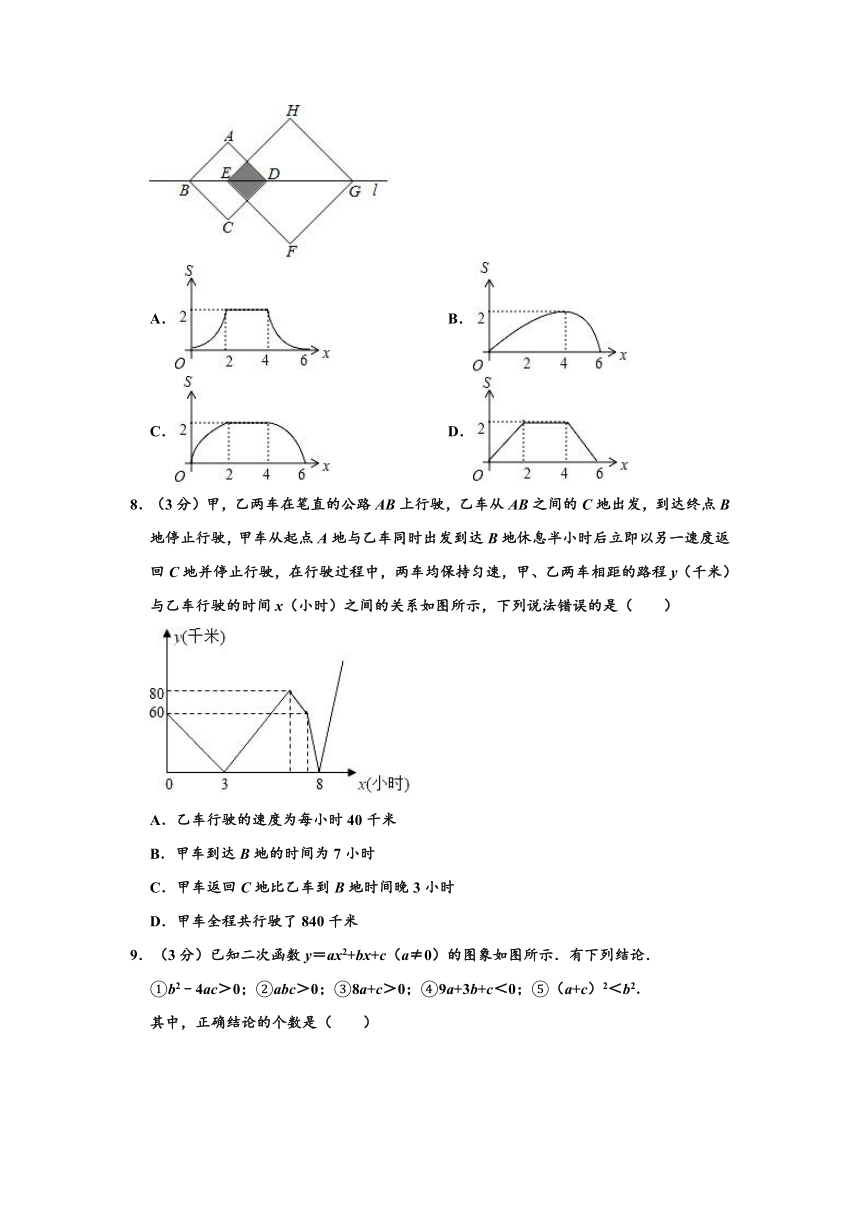
7.(3分)如图,正方形ABCD和正方形EFGH的对角线BD,EG都在直线l上,将正方形ABCD沿着直线l从点D与点E重合开始向右平移,直到点B与点G重合为止,设点D平移的距离为x,,,两个正方形重合部分的面积为S,则S关于x的函数图象大致为( )
A. B.
C. D.
8.(3分)甲,乙两车在笔直的公路AB上行驶,乙车从AB之间的C地出发,到达终点B地停止行驶,甲车从起点A地与乙车同时出发到达B地休息半小时后立即以另一速度返回C地并停止行驶,在行驶过程中,两车均保持匀速,甲、乙两车相距的路程y(千米)与乙车行驶的时间x(小时)之间的关系如图所示,下列说法错误的是( )
A.乙车行驶的速度为每小时40千米
B.甲车到达B地的时间为7小时
C.甲车返回C地比乙车到B地时间晚3小时
D.甲车全程共行驶了840千米
9.(3分)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示.有下列结论.
①b2﹣4ac>0;②abc>0;③8a+c>0;④9a+3b+c<0;⑤(a+c)2<b2.
其中,正确结论的个数是( )
A.2 B.3 C.4 D.5
10.(3分)如图,菱形ABCD的边长为4,∠A=60°,E是边AD的中点,F是边AB上的一个动点将线段EF绕着点E逆时针旋转60°得到EG,连接BG、CG,则BG+CG的最小值为( )
A.3 B.2 C.4 D.2+2
二、填空题(共6小题).
11.(3分)把多项式4ab2﹣16ac2分解因式的结果是 .
12.(3分)若,则a3﹣5a+2020= .
13.(3分)如图,在扇形AOB中,∠AOB=120°,连接AB,以OA为直径作半圆C交AB于点D,若OA=4,则阴影部分的面积为 .
14.(3分)如图,点A,点B分别在y轴,x轴上,OA=OB,点E为AB的中点,连接OE并延长交反比例函数y=(x>0)的图象于点C,过点C作CD⊥x轴于点D,点D关于直线AB的对称点恰好在反比例函数图象上,则OE﹣EC= .
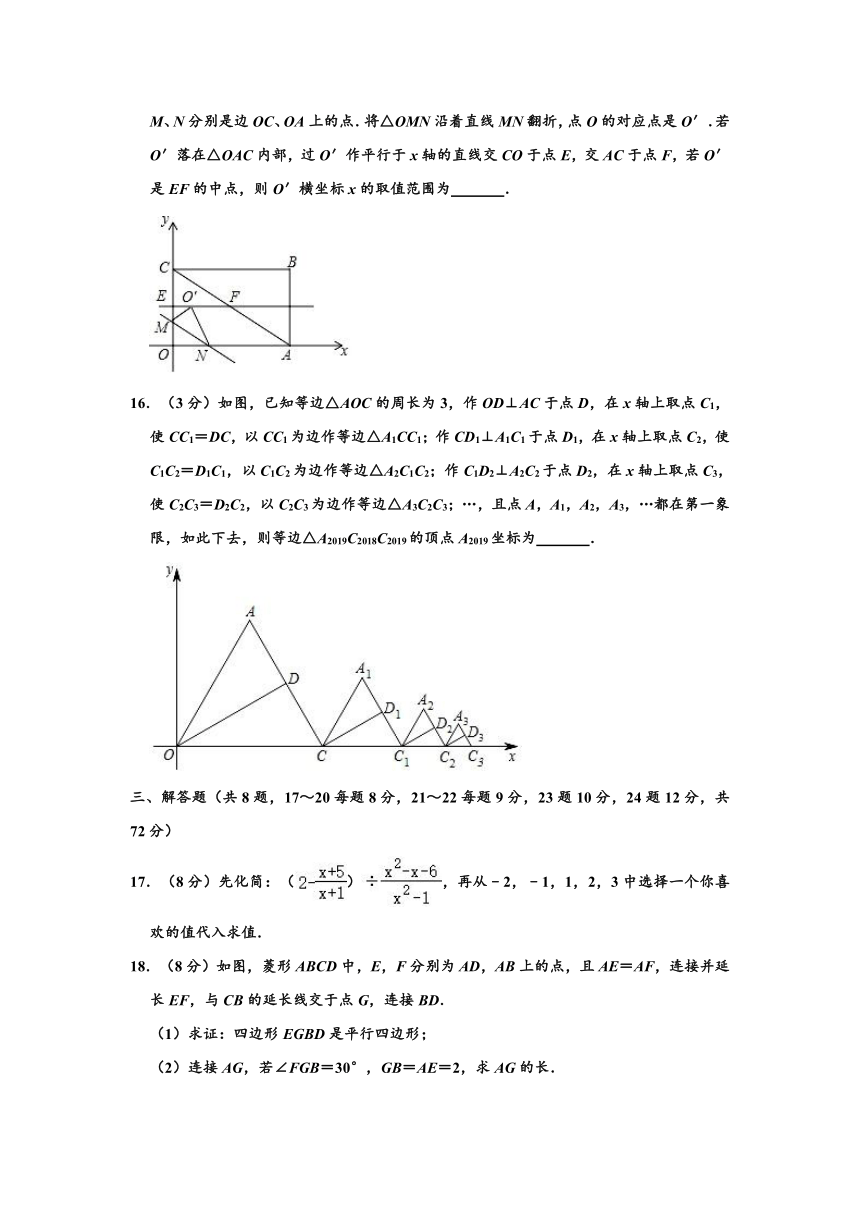
15.(3分)在直角坐标系中,矩形OABC的边OA、OC在坐标轴上,已知B(4,2),M、N分别是边OC、OA上的点.将△OMN沿着直线MN翻折,点O的对应点是O′.若O′落在△OAC内部,过O′作平行于x轴的直线交CO于点E,交AC于点F,若O′是EF的中点,则O′横坐标x的取值范围为 .
16.(3分)如图,已知等边△AOC的周长为3,作OD⊥AC于点D,在x轴上取点C1,使CC1=DC,以CC1为边作等边△A1CC1;作CD1⊥A1C1于点D1,在x轴上取点C2,使C1C2=D1C1,以C1C2为边作等边△A2C1C2;作C1D2⊥A2C2于点D2,在x轴上取点C3,使C2C3=D2C2,以C2C3为边作等边△A3C2C3;…,且点A,A1,A2,A3,…都在第一象限,如此下去,则等边△A2019C2018C2019的顶点A2019坐标为 .
三、解答题(共8题,17~20每题8分,21~22每题9分,23题10分,24题12分,共72分)
17.(8分)先化简:(),再从﹣2,﹣1,1,2,3中选择一个你喜欢的值代入求值.
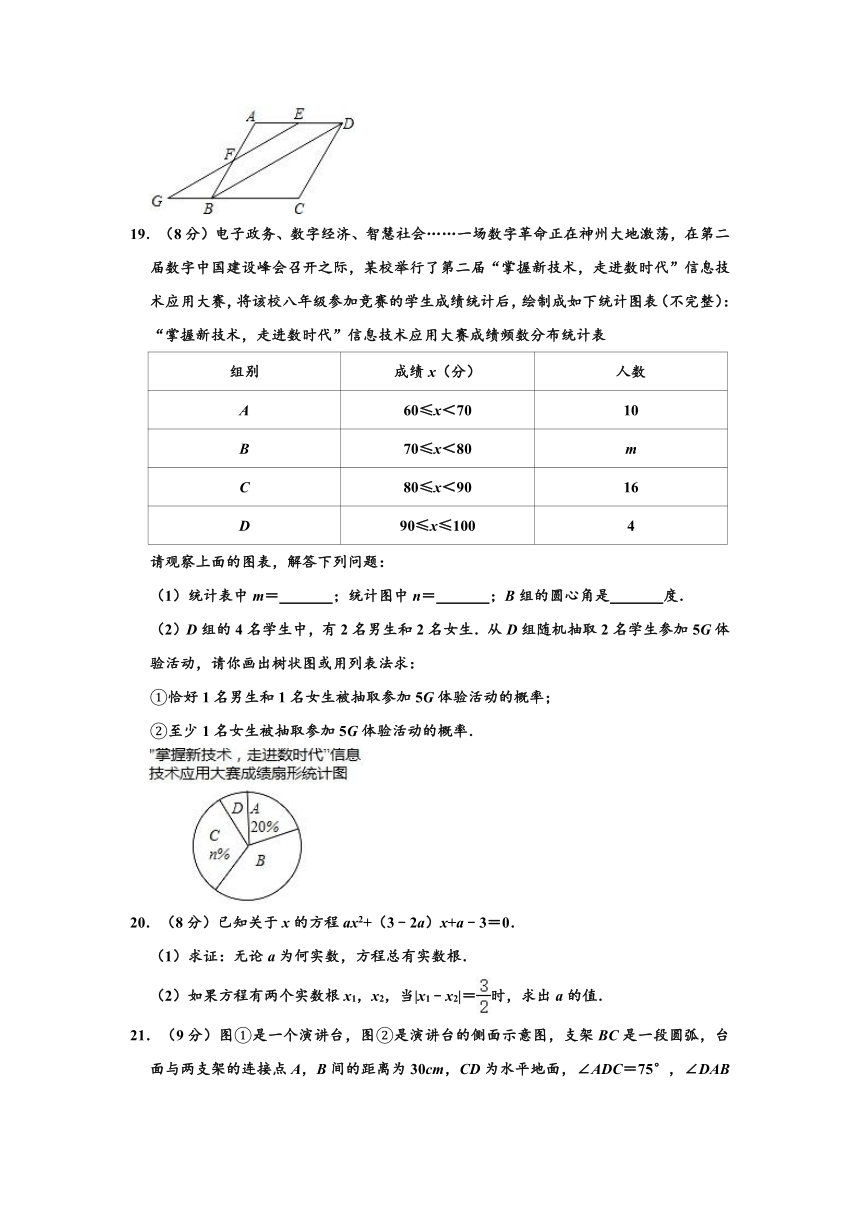
18.(8分)如图,菱形ABCD中,E,F分别为AD,AB上的点,且AE=AF,连接并延长EF,与CB的延长线交于点G,连接BD.
(1)求证:四边形EGBD是平行四边形;
(2)连接AG,若∠FGB=30°,GB=AE=2,求AG的长.
19.(8分)电子政务、数字经济、智慧社会……一场数字革命正在神州大地激荡,在第二届数字中国建设峰会召开之际,某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成如下统计图表(不完整):
“掌握新技术,走进数时代”信息技术应用大赛成绩频数分布统计表
组别 成绩x(分) 人数
A 60≤x<70 10
B 70≤x<80 m
C 80≤x<90 16
D 90≤x≤100 4
请观察上面的图表,解答下列问题:
(1)统计表中m= ;统计图中n= ;B组的圆心角是 度.
(2)D组的4名学生中,有2名男生和2名女生.从D组随机抽取2名学生参加5G体验活动,请你画出树状图或用列表法求:
①恰好1名男生和1名女生被抽取参加5G体验活动的概率;
②至少1名女生被抽取参加5G体验活动的概率.
20.(8分)已知关于x的方程ax2+(3﹣2a)x+a﹣3=0.
(1)求证:无论a为何实数,方程总有实数根.
(2)如果方程有两个实数根x1,x2,当|x1﹣x2|=时,求出a的值.
21.(9分)图①是一个演讲台,图②是演讲台的侧面示意图,支架BC是一段圆弧,台面与两支架的连接点A,B间的距离为30cm,CD为水平地面,∠ADC=75°,∠DAB=60°,BD⊥CD.
(1)求BD的长(结果保留整数,参考数据:sin75°≈0.97,cos75°≈0.26,≈1.7);
(2)如图③,若圆弧BC所在圆的圆心O在CD的延长线上,且OD=CD,求支架BC的长(结果保留根号).
22.(9分)如图,CD为⊙O的直径,直线AB与⊙O相切于点D,过C作CA⊥CB,分别交直线AB于点A和B,CA交⊙O于点E,连接DE,且AE=CD.
(1)如图1,求证:△AED≌△CDB;
(2)如图2,连接BE分别交CD和⊙O于点F,G,连接CG,DG.
i)试探究线段DG与BF之间满足的等量关系,并说明理由.
ii)若DG=,求⊙O的周长(结果保留π)
23.(10分)某水果超市经销一种进价为18元/kg的水果,根据以前的销售经验,该种水果的最佳销售期为20天,销售人员整理出这种水果的销售单价y(元/kg)与第x天(1≤x≤20)的函数图象如图所示,而第x天(1≤x≤20)的销售量m(kg)是x的一次函数,满足下表:
x(天) 1 2 3 …
m(kg) 20 24 28 …
(1)请分别写出销售单价y(元/kg)与x(天)之间及销售量m(kg)是x(天)的之间的函数关系式
(2)求在销售的第几天时,当天的利润最大,最大利润是多少?
(3)请求出试销的20天中当天的销售利润不低于1680元的天数.
24.(12分)抛物线l1:y=x2+bx+c与它的对称轴x=﹣2交于点A,且经过点B(0,﹣2).
(1)求抛物线l1的解析式;
(2)如图1,直线y=kx+2k﹣8(k<0)与抛物线l1交于点E,F,若△AEF的面积为,求k的值;
(3)如图2,将抛物线l1向下平移n(n>0)个单位长度得到抛物线l2,抛物线l2与y轴交于点C,过点C作x轴的平行线交抛物线l2于另一点D;抛物线l2的对称轴与x轴的交于点M,P为线段OC上一点,若△POM与△PCD相似,并且符合该条件的点P有且只有2个,求n的值及相应点P的坐标.
参考答案
一、选择题(共10小题).
1.(3分)一个数的相反数是﹣2020,则这个数是( )
A.2020 B.﹣2020 C. D.
解:∵一个数的相反数是﹣2020,
∴这个数是:2020.
故选:A.
2.(3分)2019年9月30日上映的电影《我和我的祖国》掀起一股观影热潮,截止12月25日票房累计达3150000000元,3150000000用科学记数法表示正确的是( )
A.315×107 B.3.15×1010 C.3.15×109 D.0.315×1010
解:3150000000=3.15×109.
故选:C.
3.(3分)下列运算正确的是( )
A.2x2?3x2=6x2 B.x3+x5=x8
C.x4÷x=x3 D.(x5)2=x7
解:A、2x2?3x2=6x4,故A错误;
B、x3与x5不是同类项,不能合并,故B错误;
C、x4÷x=x3,故C正确;
D、(x5)2=x10,故D错误;
故选:C.
4.(3分)如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图,若组成这个几何体的小正方体的个数为n,则n的最大值为( )
A.9 B.10 C.12 D.14
解:由题中所给出的主视图知物体共3列,且都是最高两层;由左视图知共三行,所以小正方体的个数最多的几何体为:第一列4个小正方体,第二列3个小正方体,第三列3个小正方体,n的最大值:4+3+3=10个.
故选:B.
5.(3分)已知直线m∥n,将一块含30°角的直角三角板按如图所示方式放置(∠ABC=30°),并且顶点A,C分别落在直线m,n上,若∠1=38°,则∠2的度数是( )
A.20° B.22° C.28° D.38°
解:
∵∠ABC=30°,∠BAC=90°,
∴∠ACB=60°,
过C作CD∥直线m,
∵直线m∥n,
∴CD∥直线m∥直线n,
∴∠1=∠ACD,∠2=∠BCD,
∵∠1=38°,
∴∠ACD=38°,
∴∠2=∠BCD=60°﹣38°=22°,
故选:B.
6.(3分)一组数据6,7,9,9,9,0,3,若去掉一个数据9,则下列统计量不发生变化的是( )
A.平均数 B.众数 C.中位数 D.方差
解:∵数据6,7,9,9,9,0,3中,9出现了3次,
∴这组数据的众数为9,
去了一个9后,这组数据中,9出现了2次,众数仍然是9,
∴众数没有变化,平均数,中位数,方差都发生了变化,
故选:B.
7.(3分)如图,正方形ABCD和正方形EFGH的对角线BD,EG都在直线l上,将正方形ABCD沿着直线l从点D与点E重合开始向右平移,直到点B与点G重合为止,设点D平移的距离为x,,,两个正方形重合部分的面积为S,则S关于x的函数图象大致为( )
A. B.
C. D.
解:如图(1),当0≤x≤2时,;
如图(2),当2<x<4时,正方形ABCD在正方形EFGH内部,
则;
如图(3),当4≤x≤6时,BG=2﹣(x﹣4)=6﹣x,
∴.综上所述,选项A符合题意.
故选:A.
8.(3分)甲,乙两车在笔直的公路AB上行驶,乙车从AB之间的C地出发,到达终点B地停止行驶,甲车从起点A地与乙车同时出发到达B地休息半小时后立即以另一速度返回C地并停止行驶,在行驶过程中,两车均保持匀速,甲、乙两车相距的路程y(千米)与乙车行驶的时间x(小时)之间的关系如图所示,下列说法错误的是( )
A.乙车行驶的速度为每小时40千米
B.甲车到达B地的时间为7小时
C.甲车返回C地比乙车到B地时间晚3小时
D.甲车全程共行驶了840千米
解:图象过(0,60)点,因此AC的距离为60千米,
过(3,0),说明经过3小时,甲追上乙,可求出速度的差为20千米/时,
两辆的最大距离为80千米,说明甲到达B地,而乙还在途中,可得甲从追上乙到B地由用了80÷20=4小时,因此甲行全程用3+4=7小时,故B选项正确的;
当甲在B地休息半小时,两车的距离减少80﹣60=20千米,说明乙车用半小时行20千米,求得乙的速度为40千米/小时,故A选项是正确的;
甲从B地到C地速度为:60÷(8﹣7.5)﹣40=80千米/小时,甲从B到C用时:360÷80=4.5,甲总时间为:3+4+0.5+4.5=12(小时),乙到B地总时间为:360÷40=9(小时),12﹣9=3,故C正确.
再根据速度差为20千米/小时,可求出甲的速度为40+20=60千米/小时,故全程为60×7=420千米;C地到B地的距离为360千米,甲从A地到B地然后返回到C共行驶360+420=780千米.故D选项是不正确的;
故选:D.
9.(3分)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示.有下列结论.
①b2﹣4ac>0;②abc>0;③8a+c>0;④9a+3b+c<0;⑤(a+c)2<b2.
其中,正确结论的个数是( )
A.2 B.3 C.4 D.5
解:抛物线与x轴有两个不同的交点,因此b2﹣4ac>0,故①正确;
抛物线开口向上,因此a>0,对称轴为x=1>0,a、b异号,因此b<0,抛物线与y轴交在负半轴,因此c<0,所以abc>0,故②正确;
由图象可知,当x=﹣2时,y=4a﹣2b+c>0,又对称轴x=﹣=1,即,b=﹣2a,所以8a+c>0,故③正确;
当x=3时,y=9a+3b+c<0,因此④正确;
当x=1时,y=a+b+c<0,当x=﹣1时,y=a﹣b+c<0,所以(a+b+c)(a﹣b+c)>0,即(a+c)2﹣b2>0,也就是(a+c)2>b2,故⑤错误,
综上所述,正确结论有:①②③④
故选:C.
10.(3分)如图,菱形ABCD的边长为4,∠A=60°,E是边AD的中点,F是边AB上的一个动点将线段EF绕着点E逆时针旋转60°得到EG,连接BG、CG,则BG+CG的最小值为( )
A.3 B.2 C.4 D.2+2
解:如图,取AB的中点N.连接EN,EC,GN,作EH⊥CD交CD的延长线于H.
∵四边形ABCD是菱形
∴AD=AB,
∵∠A=60°,
∴△ADB是等边三角形,
∴AD=BD,
∵AE=ED,AN=NB,
∴AE=AN,
∵∠A=60°,
∴△AEN是等边三角形,
∴∠AEN=∠FEG=60°,
∴∠AEF=∠NEG,
∵EA=EN,EF=EG,
∴△AEF≌△NEG(SAS),
∴∠ENG=∠A=60°,
∵∠ANE=60°,
∴∠GNB=180°﹣60°﹣60°=60°,
∴点G的运动轨迹是射线NG,
易知B,E关于射线NG对称,
∴GB=GE,
∴GB+GC=GE+GC≥EC,
在Rt△DEH中,∵∠H=90°,DE=2,∠EDH=60°,
∴DH=DE=1,EH=,
在Rt△ECH中,EC==2,
∴GB+GC≥2,
∴GB+GC的最小值为2.
故选:B.
二、填空题(共6题,每题3分,共18分)
11.(3分)把多项式4ab2﹣16ac2分解因式的结果是 4a(b+2c)(b﹣2c) .
解:4ab2﹣16ac2
=4a(b2﹣4c2)
=4a(b+2c)(b﹣2c).
故答案是:4a(b+2c)(b﹣2c).
12.(3分)若,则a3﹣5a+2020= 2024 .
解:∵a=,
∴a2=,a3=,
∴a3﹣5a+2020
=﹣5×+2020
=+2020
=+2020
=4+2020
=2024,
故答案为:2024.
13.(3分)如图,在扇形AOB中,∠AOB=120°,连接AB,以OA为直径作半圆C交AB于点D,若OA=4,则阴影部分的面积为 4π﹣3 .
解:连接OD、CD,
∵OA为圆C的直径,
∴OD⊥AB,
∵OA=OB,∠AOB=120°,
∴AD=DB,∠OAD=30°,
∴OD=OA=2,
由勾股定理得,AD==2,
∴△AOB的面积=×AB×OD=4,
∵OC=CA,BD=DA,
∴CD∥OB,CD=OB,
∴∠ACD=∠AOB=120°,△ACD的面积=×△AOB的面积=,
∴阴影部分的面积=﹣△AOB的面积﹣(﹣△ACD的面积)
=π﹣4﹣π+
=4π﹣3,
故答案为:4π﹣3.
14.(3分)如图,点A,点B分别在y轴,x轴上,OA=OB,点E为AB的中点,连接OE并延长交反比例函数y=(x>0)的图象于点C,过点C作CD⊥x轴于点D,点D关于直线AB的对称点恰好在反比例函数图象上,则OE﹣EC= .
解:∵点A,点B分别在y轴,x轴上,OA=OB,点E为AB的中点,
∴直线OC的解析式为y=x,
设C(a,a),
∵点C在反比例函数y=(x>0)的图象上,
∴a2=1,
∴a=1,
∴C(1,1),
∴D(1,0),
∴设直线AB的解析式为y=﹣x+b,则B(b,0),BD=b﹣1.
∵点B和点F关于直线AB对称,
∴BF=BD=b﹣1,
∴F(b,b﹣1),
∵F在反比例函数y=的图象上,
∴b(b﹣1)=1,
解得b1=,b2=(舍去),
∴B(,0),
∵C(1,1),
∴OD=CD=1,
∴OC=,
易证△ODC∽△OEB,
∴=,即=,
∴OE=,
∴OE﹣EC=OE﹣(OC﹣OE)=2OE﹣OC=﹣=.
故答案为:.
15.(3分)在直角坐标系中,矩形OABC的边OA、OC在坐标轴上,已知B(4,2),M、N分别是边OC、OA上的点.将△OMN沿着直线MN翻折,点O的对应点是O′.若O′落在△OAC内部,过O′作平行于x轴的直线交CO于点E,交AC于点F,若O′是EF的中点,则O′横坐标x的取值范围为 3﹣≤x≤ .
解:连接CO′交OA于K,当O′是EF中点时,K是AO中点,则OK=KA=OC=2,构建直角△OO′L,
①当M与C重合时x最大,如图1中,由重叠得:CO′=OC=2,则O′K=2﹣2,
sin45°=,则O′L=(2﹣2,
得O′L=LK=(2﹣2)=2﹣,
∴OL=2﹣(2﹣)=,
∴O′横坐标x的最大值为;
②当N与A重合时,x最小,如图2所示,
则CK的解析式为:y=﹣x+2,
设O′(x,﹣x+2),过O′作QO′⊥x轴于Q,
则O′Q=﹣x+2,AQ=4﹣x,
Rt△QO′A中,(﹣x+2)2+(4﹣x)2=42.
解得x=3﹣或3+(舍弃),
综上所述,满足条件的x的范围为3﹣≤x≤.
故答案为3﹣≤x≤.
16.(3分)如图,已知等边△AOC的周长为3,作OD⊥AC于点D,在x轴上取点C1,使CC1=DC,以CC1为边作等边△A1CC1;作CD1⊥A1C1于点D1,在x轴上取点C2,使C1C2=D1C1,以C1C2为边作等边△A2C1C2;作C1D2⊥A2C2于点D2,在x轴上取点C3,使C2C3=D2C2,以C2C3为边作等边△A3C2C3;…,且点A,A1,A2,A3,…都在第一象限,如此下去,则等边△A2019C2018C2019的顶点A2019坐标为 (,) .
解:解:∵等边△A1C1C2的周长为3,作OD⊥AC于点D,
∴OC=1,C1C2=CD=OC=,
∴OC,CC1,C1C2,C2C3,…,C2018C2019的长分别为1,,,,…,,
OC2019=OC+CC1+C1C2+C2C3,…+C2018C2019=1++++…+=,
等边△A2019C2018C2019顶点A2019的横坐标=﹣=,
等边△A2019C2018C2019顶点A2019的纵坐标=×=.
故答案为:(,).
三、解答题(共8题,17~20每题8分,21~22每题9分,23题10分,24题12分,共72分)
17.(8分)先化简:(),再从﹣2,﹣1,1,2,3中选择一个你喜欢的值代入求值.
解:原式=[﹣]?
=?
=,
当x=﹣1,1,﹣2,3时,分式没有意义,
当x=2时,原式=.
18.(8分)如图,菱形ABCD中,E,F分别为AD,AB上的点,且AE=AF,连接并延长EF,与CB的延长线交于点G,连接BD.
(1)求证:四边形EGBD是平行四边形;
(2)连接AG,若∠FGB=30°,GB=AE=2,求AG的长.
【解答】证明:(1)连接AC,如图1:
∵四边形ABCD是菱形,
∴AC平分∠DAB,且AC⊥BD,
∵AF=AE,
∴AC⊥EF,
∴EG∥BD.
又∵菱形ABCD中,ED∥BG,
∴四边形EGBD是平行四边形.
(2)过点A作AH⊥BC于H.
∵∠FGB=30°,
∴∠DBC=30°,
∴∠ABH=2∠DBC=60°,
∵GB=AE=2,
∴AB=AD=4,
在Rt△ABH中,∠AHB=90°,
∴AH=2,BH=2.
∴GH=4,
∴AG===2.
19.(8分)电子政务、数字经济、智慧社会……一场数字革命正在神州大地激荡,在第二届数字中国建设峰会召开之际,某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成如下统计图表(不完整):
“掌握新技术,走进数时代”信息技术应用大赛成绩频数分布统计表
组别 成绩x(分) 人数
A 60≤x<70 10
B 70≤x<80 m
C 80≤x<90 16
D 90≤x≤100 4
请观察上面的图表,解答下列问题:
(1)统计表中m= 20 ;统计图中n= 32 ;B组的圆心角是 144 度.
(2)D组的4名学生中,有2名男生和2名女生.从D组随机抽取2名学生参加5G体验活动,请你画出树状图或用列表法求:
①恰好1名男生和1名女生被抽取参加5G体验活动的概率;
②至少1名女生被抽取参加5G体验活动的概率.
解:(1)被调查的总人数为10÷20%=50,
则m=50﹣(10+16+4)=20,
n%=×100%=32%,即n=32,
D组的圆心角是360°×=144°,
故答案为:20、32、144;
(2)①设男同学标记为A、B;女学生标记为1、2,可能出现的所有结果列表如下:
A B 1 2
A / (B,A) (1,A) (2,A)
B (A,B) / (1,B) (2,B)
1 (A,1) (B,1) / (2,1)
2 (A,2) (B,2) (1,2) /
共有 12 种可能的结果,且每种的可能性相同,其中刚好抽到一男一女的结果有8种,
∴恰好1名男生和1名女生被抽取参加5G体验活动的概率为=;
②∵至少1名女生被抽取参加5G体验活动的有10种结果,
∴至少1名女生被抽取参加5G体验活动的概率为=.
20.(8分)已知关于x的方程ax2+(3﹣2a)x+a﹣3=0.
(1)求证:无论a为何实数,方程总有实数根.
(2)如果方程有两个实数根x1,x2,当|x1﹣x2|=时,求出a的值.
【解答】(1)证明:①当a=0时,方程为3x﹣3=0,是一元一次方程,有实数根;
②当a≠0时,方程是一元二次方程,
∵关于x的方程ax2+(3﹣2a)x+a﹣3=0中,△=(3﹣2a)2﹣4a(a﹣3)=9>0,
∴无论a为何实数,方程总有实数根.
(2)解:如果方程的两个实数根x1,x2,则x1+x2=,x1?x2=,
∵|x1﹣x2|=,
∴=,
解得a=±2.
故a的值是﹣2或2.
21.(9分)图①是一个演讲台,图②是演讲台的侧面示意图,支架BC是一段圆弧,台面与两支架的连接点A,B间的距离为30cm,CD为水平地面,∠ADC=75°,∠DAB=60°,BD⊥CD.
(1)求BD的长(结果保留整数,参考数据:sin75°≈0.97,cos75°≈0.26,≈1.7);
(2)如图③,若圆弧BC所在圆的圆心O在CD的延长线上,且OD=CD,求支架BC的长(结果保留根号).
解:(1)过点B作BE⊥AD于点E,
在Rt△ABE中,AB=30 cm,∠DAB=60°,
∴BE=AB?sin∠DAB=30×=15(cm)
∵BD⊥DC,∠ADC=75°,
∴∠ADB=15°,
∴∠EBD=75°.
在Rt△DBE中,BD=≈≈98(cm)
(2)连接BC,OB.
∵BD⊥OC,OD=CD,
∴BC=OB.
又∵OB=OC,
∴△OBC是等边三角形,
∴∠BOC=60°,
∴OB===(cm),
∴弧BC的长为=(cm).
∴支架BC的长为 cm
22.(9分)如图,CD为⊙O的直径,直线AB与⊙O相切于点D,过C作CA⊥CB,分别交直线AB于点A和B,CA交⊙O于点E,连接DE,且AE=CD.
(1)如图1,求证:△AED≌△CDB;
(2)如图2,连接BE分别交CD和⊙O于点F,G,连接CG,DG.
i)试探究线段DG与BF之间满足的等量关系,并说明理由.
ii)若DG=,求⊙O的周长(结果保留π)
解:(1)如图1中,
∵CD是直径,
∴∠CED=90°,
∵AB是⊙O的切线,
∴CD⊥AB,
∴∠AED=∠CDB=90°,
∵∠ACB=∠AED=90°,
∴DE∥BC,
∴∠ADE=∠B,
∵AE=CD,
∴△AED≌△CDB.
(2)i)如图2中,结论:BF=2DG.理由如下:
∵△AED≌△CDB,
∴DE=DB,
∴∠DEB=∠DBE,
∵∠BDG+∠CDG=90°,∠CDG+∠DCG=90°,
∴∠BDG=∠DCG=∠DEB=∠DBG,
∴DG=GB,
∵∠DFG+∠DBF=90°,∠FDG+∠BDG=90°,
∴∠GFD=∠GDF,
∴DG=GF=GB,
∴BF=2DG.
ii)如图2中,设AD=BC=y,DE=DB=z,
∵DE∥BC,
∴=,
∴=
整理得y2﹣yz﹣z2=0,
∴y=z或y=z(舍弃),
∵DE∥BC,
∴===,
∴=,
∴EF=﹣,
设DF=2k,CF=(1+)k,
∵EF?FG=DF?CF,
∴(﹣)?=2k?(1+)k,
∴k=,
∴CD=DF+CF=+1,
∴OC=,
⊙O的周长为(+1)π.
23.(10分)某水果超市经销一种进价为18元/kg的水果,根据以前的销售经验,该种水果的最佳销售期为20天,销售人员整理出这种水果的销售单价y(元/kg)与第x天(1≤x≤20)的函数图象如图所示,而第x天(1≤x≤20)的销售量m(kg)是x的一次函数,满足下表:
x(天) 1 2 3 …
m(kg) 20 24 28 …
(1)请分别写出销售单价y(元/kg)与x(天)之间及销售量m(kg)是x(天)的之间的函数关系式
(2)求在销售的第几天时,当天的利润最大,最大利润是多少?
(3)请求出试销的20天中当天的销售利润不低于1680元的天数.
解:(1)当1≤x≤7时,y=60;
当8≤x≤20时,设y=kx+b,
将(8,50)、(18,40)代入得,
解得,
∴y=﹣x+58;
综上,y=;
设m=ax+c,
将(1,20)、(2,24)代入得,
解得,
则m=4x+16(0≤x≤20,且x为整数);
(2)设当天的总利润为w,
当1≤x≤7时,w=(60﹣18)(4x+16)=168x+672,
则x=7时,w取得最大值,最大值为1848元;
当8≤x≤20时,w=(﹣x+58﹣18)(4x+16)
=﹣4x2+144x+640
=﹣4(x﹣18)2+1936,
∴当x=18时,w取得最大值,最大利润为1936元;
综上,在销售的第18天时,当天的利润最大,最大利润是1936元;
(3)当1≤x≤7时,168x+672≥1680,
解得x≥6,
∴此时满足条件的天数为第6、7这2天;
当8≤x≤20时,﹣4(x﹣18)2+1936≥1680,
解得10≤x≤26,
又∵x≤20,
∴10≤x≤20,
∴此时满足条件的天数有11天;
综上,试销的20天中当天的销售利润不低于1680元的有13天.
24.(12分)抛物线l1:y=x2+bx+c与它的对称轴x=﹣2交于点A,且经过点B(0,﹣2).
(1)求抛物线l1的解析式;
(2)如图1,直线y=kx+2k﹣8(k<0)与抛物线l1交于点E,F,若△AEF的面积为,求k的值;
(3)如图2,将抛物线l1向下平移n(n>0)个单位长度得到抛物线l2,抛物线l2与y轴交于点C,过点C作x轴的平行线交抛物线l2于另一点D;抛物线l2的对称轴与x轴的交于点M,P为线段OC上一点,若△POM与△PCD相似,并且符合该条件的点P有且只有2个,求n的值及相应点P的坐标.
解:(1)根据题意有,
解得,
∴抛物线l1的解析式为y=x2+4x﹣2.
(2)如图1,设直线y=kx+2k﹣8与抛物线l1的对称轴交点为G,则G(﹣2,﹣8),
又可得抛物线l1的顶点A(﹣2,﹣6),
∴AG=2,
S△AEF=S△AGE﹣S△AGF
=AG?(﹣2﹣xE)﹣AG?(﹣2﹣xF)
=AG?(xF﹣xE),
又∵S△AEF=2,AG=2,
∴xF﹣xE=2,
将抛物线l1与直线y=kx+2k﹣8联立得,
消去y得x2+4x﹣2=kx+2k﹣8,
整理得x2+(4﹣k)x﹣2k+6=0,得x=,
∴xF﹣xE=,
∴=2,
解得k=±4,
又k<0,
∴k=﹣4.
(3)设抛物线l2的解析式为y=x2+4x﹣2﹣m,
∴C(0,﹣2﹣n),D(﹣4,﹣2﹣n),M(﹣2,0)
设P(0,t).
①当△PCD∽△MOP时,=,
∴=,
∴t2+(n+2)t+8=0;
②当△PCD∽△POM时,=,
∴=,
∴t=﹣;
(Ⅰ)当方程①有两个相等实数根时,
△=(n+2)2﹣4×1×8=0,
解得n=±4﹣2,
又n>0,
∴n=4﹣2,
此时方程①有两个相等实根t1=t2=﹣2,方程②有一个实数根t=﹣;
∴n=4﹣2,
此时点P的坐标为(0,﹣2)和(0,﹣);
(Ⅱ)当方程①有两个不相等的实数根时,
把②代入①,得:﹣+8=0,即(n+2)2=36,
解得n1=4,n2=﹣8,
又n>0,
∴n=4,
此时方程①有两个不相等的实数根,t1=﹣2,t2=﹣4,方程①有一个实数根t=﹣2;
∴n=4,
此时点P坐标为(0,﹣2)和(0,﹣4),
综上,当n=4﹣2时,点P的坐标为(0,﹣2)和(0,﹣);当n=4时,点P坐标为(0,﹣2)和(0,﹣4).
一、选择题(共10小题).
1.(3分)一个数的相反数是﹣2020,则这个数是( )
A.2020 B.﹣2020 C. D.
2.(3分)2019年9月30日上映的电影《我和我的祖国》掀起一股观影热潮,截止12月25日票房累计达3150000000元,3150000000用科学记数法表示正确的是( )
A.315×107 B.3.15×1010 C.3.15×109 D.0.315×1010
3.(3分)下列运算正确的是( )
A.2x2?3x2=6x2 B.x3+x5=x8
C.x4÷x=x3 D.(x5)2=x7
4.(3分)如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图,若组成这个几何体的小正方体的个数为n,则n的最大值为( )
A.9 B.10 C.12 D.14
5.(3分)已知直线m∥n,将一块含30°角的直角三角板按如图所示方式放置(∠ABC=30°),并且顶点A,C分别落在直线m,n上,若∠1=38°,则∠2的度数是( )
A.20° B.22° C.28° D.38°
6.(3分)一组数据6,7,9,9,9,0,3,若去掉一个数据9,则下列统计量不发生变化的是( )
A.平均数 B.众数 C.中位数 D.方差
7.(3分)如图,正方形ABCD和正方形EFGH的对角线BD,EG都在直线l上,将正方形ABCD沿着直线l从点D与点E重合开始向右平移,直到点B与点G重合为止,设点D平移的距离为x,,,两个正方形重合部分的面积为S,则S关于x的函数图象大致为( )
A. B.
C. D.
8.(3分)甲,乙两车在笔直的公路AB上行驶,乙车从AB之间的C地出发,到达终点B地停止行驶,甲车从起点A地与乙车同时出发到达B地休息半小时后立即以另一速度返回C地并停止行驶,在行驶过程中,两车均保持匀速,甲、乙两车相距的路程y(千米)与乙车行驶的时间x(小时)之间的关系如图所示,下列说法错误的是( )
A.乙车行驶的速度为每小时40千米
B.甲车到达B地的时间为7小时
C.甲车返回C地比乙车到B地时间晚3小时
D.甲车全程共行驶了840千米
9.(3分)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示.有下列结论.
①b2﹣4ac>0;②abc>0;③8a+c>0;④9a+3b+c<0;⑤(a+c)2<b2.
其中,正确结论的个数是( )
A.2 B.3 C.4 D.5
10.(3分)如图,菱形ABCD的边长为4,∠A=60°,E是边AD的中点,F是边AB上的一个动点将线段EF绕着点E逆时针旋转60°得到EG,连接BG、CG,则BG+CG的最小值为( )
A.3 B.2 C.4 D.2+2
二、填空题(共6小题).
11.(3分)把多项式4ab2﹣16ac2分解因式的结果是 .
12.(3分)若,则a3﹣5a+2020= .
13.(3分)如图,在扇形AOB中,∠AOB=120°,连接AB,以OA为直径作半圆C交AB于点D,若OA=4,则阴影部分的面积为 .
14.(3分)如图,点A,点B分别在y轴,x轴上,OA=OB,点E为AB的中点,连接OE并延长交反比例函数y=(x>0)的图象于点C,过点C作CD⊥x轴于点D,点D关于直线AB的对称点恰好在反比例函数图象上,则OE﹣EC= .
15.(3分)在直角坐标系中,矩形OABC的边OA、OC在坐标轴上,已知B(4,2),M、N分别是边OC、OA上的点.将△OMN沿着直线MN翻折,点O的对应点是O′.若O′落在△OAC内部,过O′作平行于x轴的直线交CO于点E,交AC于点F,若O′是EF的中点,则O′横坐标x的取值范围为 .
16.(3分)如图,已知等边△AOC的周长为3,作OD⊥AC于点D,在x轴上取点C1,使CC1=DC,以CC1为边作等边△A1CC1;作CD1⊥A1C1于点D1,在x轴上取点C2,使C1C2=D1C1,以C1C2为边作等边△A2C1C2;作C1D2⊥A2C2于点D2,在x轴上取点C3,使C2C3=D2C2,以C2C3为边作等边△A3C2C3;…,且点A,A1,A2,A3,…都在第一象限,如此下去,则等边△A2019C2018C2019的顶点A2019坐标为 .
三、解答题(共8题,17~20每题8分,21~22每题9分,23题10分,24题12分,共72分)
17.(8分)先化简:(),再从﹣2,﹣1,1,2,3中选择一个你喜欢的值代入求值.
18.(8分)如图,菱形ABCD中,E,F分别为AD,AB上的点,且AE=AF,连接并延长EF,与CB的延长线交于点G,连接BD.
(1)求证:四边形EGBD是平行四边形;
(2)连接AG,若∠FGB=30°,GB=AE=2,求AG的长.
19.(8分)电子政务、数字经济、智慧社会……一场数字革命正在神州大地激荡,在第二届数字中国建设峰会召开之际,某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成如下统计图表(不完整):
“掌握新技术,走进数时代”信息技术应用大赛成绩频数分布统计表
组别 成绩x(分) 人数
A 60≤x<70 10
B 70≤x<80 m
C 80≤x<90 16
D 90≤x≤100 4
请观察上面的图表,解答下列问题:
(1)统计表中m= ;统计图中n= ;B组的圆心角是 度.
(2)D组的4名学生中,有2名男生和2名女生.从D组随机抽取2名学生参加5G体验活动,请你画出树状图或用列表法求:
①恰好1名男生和1名女生被抽取参加5G体验活动的概率;
②至少1名女生被抽取参加5G体验活动的概率.
20.(8分)已知关于x的方程ax2+(3﹣2a)x+a﹣3=0.
(1)求证:无论a为何实数,方程总有实数根.
(2)如果方程有两个实数根x1,x2,当|x1﹣x2|=时,求出a的值.
21.(9分)图①是一个演讲台,图②是演讲台的侧面示意图,支架BC是一段圆弧,台面与两支架的连接点A,B间的距离为30cm,CD为水平地面,∠ADC=75°,∠DAB=60°,BD⊥CD.
(1)求BD的长(结果保留整数,参考数据:sin75°≈0.97,cos75°≈0.26,≈1.7);
(2)如图③,若圆弧BC所在圆的圆心O在CD的延长线上,且OD=CD,求支架BC的长(结果保留根号).
22.(9分)如图,CD为⊙O的直径,直线AB与⊙O相切于点D,过C作CA⊥CB,分别交直线AB于点A和B,CA交⊙O于点E,连接DE,且AE=CD.
(1)如图1,求证:△AED≌△CDB;
(2)如图2,连接BE分别交CD和⊙O于点F,G,连接CG,DG.
i)试探究线段DG与BF之间满足的等量关系,并说明理由.
ii)若DG=,求⊙O的周长(结果保留π)
23.(10分)某水果超市经销一种进价为18元/kg的水果,根据以前的销售经验,该种水果的最佳销售期为20天,销售人员整理出这种水果的销售单价y(元/kg)与第x天(1≤x≤20)的函数图象如图所示,而第x天(1≤x≤20)的销售量m(kg)是x的一次函数,满足下表:
x(天) 1 2 3 …
m(kg) 20 24 28 …
(1)请分别写出销售单价y(元/kg)与x(天)之间及销售量m(kg)是x(天)的之间的函数关系式
(2)求在销售的第几天时,当天的利润最大,最大利润是多少?
(3)请求出试销的20天中当天的销售利润不低于1680元的天数.
24.(12分)抛物线l1:y=x2+bx+c与它的对称轴x=﹣2交于点A,且经过点B(0,﹣2).
(1)求抛物线l1的解析式;
(2)如图1,直线y=kx+2k﹣8(k<0)与抛物线l1交于点E,F,若△AEF的面积为,求k的值;
(3)如图2,将抛物线l1向下平移n(n>0)个单位长度得到抛物线l2,抛物线l2与y轴交于点C,过点C作x轴的平行线交抛物线l2于另一点D;抛物线l2的对称轴与x轴的交于点M,P为线段OC上一点,若△POM与△PCD相似,并且符合该条件的点P有且只有2个,求n的值及相应点P的坐标.
参考答案
一、选择题(共10小题).
1.(3分)一个数的相反数是﹣2020,则这个数是( )
A.2020 B.﹣2020 C. D.
解:∵一个数的相反数是﹣2020,
∴这个数是:2020.
故选:A.
2.(3分)2019年9月30日上映的电影《我和我的祖国》掀起一股观影热潮,截止12月25日票房累计达3150000000元,3150000000用科学记数法表示正确的是( )
A.315×107 B.3.15×1010 C.3.15×109 D.0.315×1010
解:3150000000=3.15×109.
故选:C.
3.(3分)下列运算正确的是( )
A.2x2?3x2=6x2 B.x3+x5=x8
C.x4÷x=x3 D.(x5)2=x7
解:A、2x2?3x2=6x4,故A错误;
B、x3与x5不是同类项,不能合并,故B错误;
C、x4÷x=x3,故C正确;
D、(x5)2=x10,故D错误;
故选:C.
4.(3分)如图是由一些完全相同的小正方体搭成的几何体的主视图和左视图,若组成这个几何体的小正方体的个数为n,则n的最大值为( )
A.9 B.10 C.12 D.14
解:由题中所给出的主视图知物体共3列,且都是最高两层;由左视图知共三行,所以小正方体的个数最多的几何体为:第一列4个小正方体,第二列3个小正方体,第三列3个小正方体,n的最大值:4+3+3=10个.
故选:B.
5.(3分)已知直线m∥n,将一块含30°角的直角三角板按如图所示方式放置(∠ABC=30°),并且顶点A,C分别落在直线m,n上,若∠1=38°,则∠2的度数是( )
A.20° B.22° C.28° D.38°
解:
∵∠ABC=30°,∠BAC=90°,
∴∠ACB=60°,
过C作CD∥直线m,
∵直线m∥n,
∴CD∥直线m∥直线n,
∴∠1=∠ACD,∠2=∠BCD,
∵∠1=38°,
∴∠ACD=38°,
∴∠2=∠BCD=60°﹣38°=22°,
故选:B.
6.(3分)一组数据6,7,9,9,9,0,3,若去掉一个数据9,则下列统计量不发生变化的是( )
A.平均数 B.众数 C.中位数 D.方差
解:∵数据6,7,9,9,9,0,3中,9出现了3次,
∴这组数据的众数为9,
去了一个9后,这组数据中,9出现了2次,众数仍然是9,
∴众数没有变化,平均数,中位数,方差都发生了变化,
故选:B.
7.(3分)如图,正方形ABCD和正方形EFGH的对角线BD,EG都在直线l上,将正方形ABCD沿着直线l从点D与点E重合开始向右平移,直到点B与点G重合为止,设点D平移的距离为x,,,两个正方形重合部分的面积为S,则S关于x的函数图象大致为( )
A. B.
C. D.
解:如图(1),当0≤x≤2时,;
如图(2),当2<x<4时,正方形ABCD在正方形EFGH内部,
则;
如图(3),当4≤x≤6时,BG=2﹣(x﹣4)=6﹣x,
∴.综上所述,选项A符合题意.
故选:A.
8.(3分)甲,乙两车在笔直的公路AB上行驶,乙车从AB之间的C地出发,到达终点B地停止行驶,甲车从起点A地与乙车同时出发到达B地休息半小时后立即以另一速度返回C地并停止行驶,在行驶过程中,两车均保持匀速,甲、乙两车相距的路程y(千米)与乙车行驶的时间x(小时)之间的关系如图所示,下列说法错误的是( )
A.乙车行驶的速度为每小时40千米
B.甲车到达B地的时间为7小时
C.甲车返回C地比乙车到B地时间晚3小时
D.甲车全程共行驶了840千米
解:图象过(0,60)点,因此AC的距离为60千米,
过(3,0),说明经过3小时,甲追上乙,可求出速度的差为20千米/时,
两辆的最大距离为80千米,说明甲到达B地,而乙还在途中,可得甲从追上乙到B地由用了80÷20=4小时,因此甲行全程用3+4=7小时,故B选项正确的;
当甲在B地休息半小时,两车的距离减少80﹣60=20千米,说明乙车用半小时行20千米,求得乙的速度为40千米/小时,故A选项是正确的;
甲从B地到C地速度为:60÷(8﹣7.5)﹣40=80千米/小时,甲从B到C用时:360÷80=4.5,甲总时间为:3+4+0.5+4.5=12(小时),乙到B地总时间为:360÷40=9(小时),12﹣9=3,故C正确.
再根据速度差为20千米/小时,可求出甲的速度为40+20=60千米/小时,故全程为60×7=420千米;C地到B地的距离为360千米,甲从A地到B地然后返回到C共行驶360+420=780千米.故D选项是不正确的;
故选:D.
9.(3分)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示.有下列结论.
①b2﹣4ac>0;②abc>0;③8a+c>0;④9a+3b+c<0;⑤(a+c)2<b2.
其中,正确结论的个数是( )
A.2 B.3 C.4 D.5
解:抛物线与x轴有两个不同的交点,因此b2﹣4ac>0,故①正确;
抛物线开口向上,因此a>0,对称轴为x=1>0,a、b异号,因此b<0,抛物线与y轴交在负半轴,因此c<0,所以abc>0,故②正确;
由图象可知,当x=﹣2时,y=4a﹣2b+c>0,又对称轴x=﹣=1,即,b=﹣2a,所以8a+c>0,故③正确;
当x=3时,y=9a+3b+c<0,因此④正确;
当x=1时,y=a+b+c<0,当x=﹣1时,y=a﹣b+c<0,所以(a+b+c)(a﹣b+c)>0,即(a+c)2﹣b2>0,也就是(a+c)2>b2,故⑤错误,
综上所述,正确结论有:①②③④
故选:C.
10.(3分)如图,菱形ABCD的边长为4,∠A=60°,E是边AD的中点,F是边AB上的一个动点将线段EF绕着点E逆时针旋转60°得到EG,连接BG、CG,则BG+CG的最小值为( )
A.3 B.2 C.4 D.2+2
解:如图,取AB的中点N.连接EN,EC,GN,作EH⊥CD交CD的延长线于H.
∵四边形ABCD是菱形
∴AD=AB,
∵∠A=60°,
∴△ADB是等边三角形,
∴AD=BD,
∵AE=ED,AN=NB,
∴AE=AN,
∵∠A=60°,
∴△AEN是等边三角形,
∴∠AEN=∠FEG=60°,
∴∠AEF=∠NEG,
∵EA=EN,EF=EG,
∴△AEF≌△NEG(SAS),
∴∠ENG=∠A=60°,
∵∠ANE=60°,
∴∠GNB=180°﹣60°﹣60°=60°,
∴点G的运动轨迹是射线NG,
易知B,E关于射线NG对称,
∴GB=GE,
∴GB+GC=GE+GC≥EC,
在Rt△DEH中,∵∠H=90°,DE=2,∠EDH=60°,
∴DH=DE=1,EH=,
在Rt△ECH中,EC==2,
∴GB+GC≥2,
∴GB+GC的最小值为2.
故选:B.
二、填空题(共6题,每题3分,共18分)
11.(3分)把多项式4ab2﹣16ac2分解因式的结果是 4a(b+2c)(b﹣2c) .
解:4ab2﹣16ac2
=4a(b2﹣4c2)
=4a(b+2c)(b﹣2c).
故答案是:4a(b+2c)(b﹣2c).
12.(3分)若,则a3﹣5a+2020= 2024 .
解:∵a=,
∴a2=,a3=,
∴a3﹣5a+2020
=﹣5×+2020
=+2020
=+2020
=4+2020
=2024,
故答案为:2024.
13.(3分)如图,在扇形AOB中,∠AOB=120°,连接AB,以OA为直径作半圆C交AB于点D,若OA=4,则阴影部分的面积为 4π﹣3 .
解:连接OD、CD,
∵OA为圆C的直径,
∴OD⊥AB,
∵OA=OB,∠AOB=120°,
∴AD=DB,∠OAD=30°,
∴OD=OA=2,
由勾股定理得,AD==2,
∴△AOB的面积=×AB×OD=4,
∵OC=CA,BD=DA,
∴CD∥OB,CD=OB,
∴∠ACD=∠AOB=120°,△ACD的面积=×△AOB的面积=,
∴阴影部分的面积=﹣△AOB的面积﹣(﹣△ACD的面积)
=π﹣4﹣π+
=4π﹣3,
故答案为:4π﹣3.
14.(3分)如图,点A,点B分别在y轴,x轴上,OA=OB,点E为AB的中点,连接OE并延长交反比例函数y=(x>0)的图象于点C,过点C作CD⊥x轴于点D,点D关于直线AB的对称点恰好在反比例函数图象上,则OE﹣EC= .
解:∵点A,点B分别在y轴,x轴上,OA=OB,点E为AB的中点,
∴直线OC的解析式为y=x,
设C(a,a),
∵点C在反比例函数y=(x>0)的图象上,
∴a2=1,
∴a=1,
∴C(1,1),
∴D(1,0),
∴设直线AB的解析式为y=﹣x+b,则B(b,0),BD=b﹣1.
∵点B和点F关于直线AB对称,
∴BF=BD=b﹣1,
∴F(b,b﹣1),
∵F在反比例函数y=的图象上,
∴b(b﹣1)=1,
解得b1=,b2=(舍去),
∴B(,0),
∵C(1,1),
∴OD=CD=1,
∴OC=,
易证△ODC∽△OEB,
∴=,即=,
∴OE=,
∴OE﹣EC=OE﹣(OC﹣OE)=2OE﹣OC=﹣=.
故答案为:.
15.(3分)在直角坐标系中,矩形OABC的边OA、OC在坐标轴上,已知B(4,2),M、N分别是边OC、OA上的点.将△OMN沿着直线MN翻折,点O的对应点是O′.若O′落在△OAC内部,过O′作平行于x轴的直线交CO于点E,交AC于点F,若O′是EF的中点,则O′横坐标x的取值范围为 3﹣≤x≤ .
解:连接CO′交OA于K,当O′是EF中点时,K是AO中点,则OK=KA=OC=2,构建直角△OO′L,
①当M与C重合时x最大,如图1中,由重叠得:CO′=OC=2,则O′K=2﹣2,
sin45°=,则O′L=(2﹣2,
得O′L=LK=(2﹣2)=2﹣,
∴OL=2﹣(2﹣)=,
∴O′横坐标x的最大值为;
②当N与A重合时,x最小,如图2所示,
则CK的解析式为:y=﹣x+2,
设O′(x,﹣x+2),过O′作QO′⊥x轴于Q,
则O′Q=﹣x+2,AQ=4﹣x,
Rt△QO′A中,(﹣x+2)2+(4﹣x)2=42.
解得x=3﹣或3+(舍弃),
综上所述,满足条件的x的范围为3﹣≤x≤.
故答案为3﹣≤x≤.
16.(3分)如图,已知等边△AOC的周长为3,作OD⊥AC于点D,在x轴上取点C1,使CC1=DC,以CC1为边作等边△A1CC1;作CD1⊥A1C1于点D1,在x轴上取点C2,使C1C2=D1C1,以C1C2为边作等边△A2C1C2;作C1D2⊥A2C2于点D2,在x轴上取点C3,使C2C3=D2C2,以C2C3为边作等边△A3C2C3;…,且点A,A1,A2,A3,…都在第一象限,如此下去,则等边△A2019C2018C2019的顶点A2019坐标为 (,) .
解:解:∵等边△A1C1C2的周长为3,作OD⊥AC于点D,
∴OC=1,C1C2=CD=OC=,
∴OC,CC1,C1C2,C2C3,…,C2018C2019的长分别为1,,,,…,,
OC2019=OC+CC1+C1C2+C2C3,…+C2018C2019=1++++…+=,
等边△A2019C2018C2019顶点A2019的横坐标=﹣=,
等边△A2019C2018C2019顶点A2019的纵坐标=×=.
故答案为:(,).
三、解答题(共8题,17~20每题8分,21~22每题9分,23题10分,24题12分,共72分)
17.(8分)先化简:(),再从﹣2,﹣1,1,2,3中选择一个你喜欢的值代入求值.
解:原式=[﹣]?
=?
=,
当x=﹣1,1,﹣2,3时,分式没有意义,
当x=2时,原式=.
18.(8分)如图,菱形ABCD中,E,F分别为AD,AB上的点,且AE=AF,连接并延长EF,与CB的延长线交于点G,连接BD.
(1)求证:四边形EGBD是平行四边形;
(2)连接AG,若∠FGB=30°,GB=AE=2,求AG的长.
【解答】证明:(1)连接AC,如图1:
∵四边形ABCD是菱形,
∴AC平分∠DAB,且AC⊥BD,
∵AF=AE,
∴AC⊥EF,
∴EG∥BD.
又∵菱形ABCD中,ED∥BG,
∴四边形EGBD是平行四边形.
(2)过点A作AH⊥BC于H.
∵∠FGB=30°,
∴∠DBC=30°,
∴∠ABH=2∠DBC=60°,
∵GB=AE=2,
∴AB=AD=4,
在Rt△ABH中,∠AHB=90°,
∴AH=2,BH=2.
∴GH=4,
∴AG===2.
19.(8分)电子政务、数字经济、智慧社会……一场数字革命正在神州大地激荡,在第二届数字中国建设峰会召开之际,某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成如下统计图表(不完整):
“掌握新技术,走进数时代”信息技术应用大赛成绩频数分布统计表
组别 成绩x(分) 人数
A 60≤x<70 10
B 70≤x<80 m
C 80≤x<90 16
D 90≤x≤100 4
请观察上面的图表,解答下列问题:
(1)统计表中m= 20 ;统计图中n= 32 ;B组的圆心角是 144 度.
(2)D组的4名学生中,有2名男生和2名女生.从D组随机抽取2名学生参加5G体验活动,请你画出树状图或用列表法求:
①恰好1名男生和1名女生被抽取参加5G体验活动的概率;
②至少1名女生被抽取参加5G体验活动的概率.
解:(1)被调查的总人数为10÷20%=50,
则m=50﹣(10+16+4)=20,
n%=×100%=32%,即n=32,
D组的圆心角是360°×=144°,
故答案为:20、32、144;
(2)①设男同学标记为A、B;女学生标记为1、2,可能出现的所有结果列表如下:
A B 1 2
A / (B,A) (1,A) (2,A)
B (A,B) / (1,B) (2,B)
1 (A,1) (B,1) / (2,1)
2 (A,2) (B,2) (1,2) /
共有 12 种可能的结果,且每种的可能性相同,其中刚好抽到一男一女的结果有8种,
∴恰好1名男生和1名女生被抽取参加5G体验活动的概率为=;
②∵至少1名女生被抽取参加5G体验活动的有10种结果,
∴至少1名女生被抽取参加5G体验活动的概率为=.
20.(8分)已知关于x的方程ax2+(3﹣2a)x+a﹣3=0.
(1)求证:无论a为何实数,方程总有实数根.
(2)如果方程有两个实数根x1,x2,当|x1﹣x2|=时,求出a的值.
【解答】(1)证明:①当a=0时,方程为3x﹣3=0,是一元一次方程,有实数根;
②当a≠0时,方程是一元二次方程,
∵关于x的方程ax2+(3﹣2a)x+a﹣3=0中,△=(3﹣2a)2﹣4a(a﹣3)=9>0,
∴无论a为何实数,方程总有实数根.
(2)解:如果方程的两个实数根x1,x2,则x1+x2=,x1?x2=,
∵|x1﹣x2|=,
∴=,
解得a=±2.
故a的值是﹣2或2.
21.(9分)图①是一个演讲台,图②是演讲台的侧面示意图,支架BC是一段圆弧,台面与两支架的连接点A,B间的距离为30cm,CD为水平地面,∠ADC=75°,∠DAB=60°,BD⊥CD.
(1)求BD的长(结果保留整数,参考数据:sin75°≈0.97,cos75°≈0.26,≈1.7);
(2)如图③,若圆弧BC所在圆的圆心O在CD的延长线上,且OD=CD,求支架BC的长(结果保留根号).
解:(1)过点B作BE⊥AD于点E,
在Rt△ABE中,AB=30 cm,∠DAB=60°,
∴BE=AB?sin∠DAB=30×=15(cm)
∵BD⊥DC,∠ADC=75°,
∴∠ADB=15°,
∴∠EBD=75°.
在Rt△DBE中,BD=≈≈98(cm)
(2)连接BC,OB.
∵BD⊥OC,OD=CD,
∴BC=OB.
又∵OB=OC,
∴△OBC是等边三角形,
∴∠BOC=60°,
∴OB===(cm),
∴弧BC的长为=(cm).
∴支架BC的长为 cm
22.(9分)如图,CD为⊙O的直径,直线AB与⊙O相切于点D,过C作CA⊥CB,分别交直线AB于点A和B,CA交⊙O于点E,连接DE,且AE=CD.
(1)如图1,求证:△AED≌△CDB;
(2)如图2,连接BE分别交CD和⊙O于点F,G,连接CG,DG.
i)试探究线段DG与BF之间满足的等量关系,并说明理由.
ii)若DG=,求⊙O的周长(结果保留π)
解:(1)如图1中,
∵CD是直径,
∴∠CED=90°,
∵AB是⊙O的切线,
∴CD⊥AB,
∴∠AED=∠CDB=90°,
∵∠ACB=∠AED=90°,
∴DE∥BC,
∴∠ADE=∠B,
∵AE=CD,
∴△AED≌△CDB.
(2)i)如图2中,结论:BF=2DG.理由如下:
∵△AED≌△CDB,
∴DE=DB,
∴∠DEB=∠DBE,
∵∠BDG+∠CDG=90°,∠CDG+∠DCG=90°,
∴∠BDG=∠DCG=∠DEB=∠DBG,
∴DG=GB,
∵∠DFG+∠DBF=90°,∠FDG+∠BDG=90°,
∴∠GFD=∠GDF,
∴DG=GF=GB,
∴BF=2DG.
ii)如图2中,设AD=BC=y,DE=DB=z,
∵DE∥BC,
∴=,
∴=
整理得y2﹣yz﹣z2=0,
∴y=z或y=z(舍弃),
∵DE∥BC,
∴===,
∴=,
∴EF=﹣,
设DF=2k,CF=(1+)k,
∵EF?FG=DF?CF,
∴(﹣)?=2k?(1+)k,
∴k=,
∴CD=DF+CF=+1,
∴OC=,
⊙O的周长为(+1)π.
23.(10分)某水果超市经销一种进价为18元/kg的水果,根据以前的销售经验,该种水果的最佳销售期为20天,销售人员整理出这种水果的销售单价y(元/kg)与第x天(1≤x≤20)的函数图象如图所示,而第x天(1≤x≤20)的销售量m(kg)是x的一次函数,满足下表:
x(天) 1 2 3 …
m(kg) 20 24 28 …
(1)请分别写出销售单价y(元/kg)与x(天)之间及销售量m(kg)是x(天)的之间的函数关系式
(2)求在销售的第几天时,当天的利润最大,最大利润是多少?
(3)请求出试销的20天中当天的销售利润不低于1680元的天数.
解:(1)当1≤x≤7时,y=60;
当8≤x≤20时,设y=kx+b,
将(8,50)、(18,40)代入得,
解得,
∴y=﹣x+58;
综上,y=;
设m=ax+c,
将(1,20)、(2,24)代入得,
解得,
则m=4x+16(0≤x≤20,且x为整数);
(2)设当天的总利润为w,
当1≤x≤7时,w=(60﹣18)(4x+16)=168x+672,
则x=7时,w取得最大值,最大值为1848元;
当8≤x≤20时,w=(﹣x+58﹣18)(4x+16)
=﹣4x2+144x+640
=﹣4(x﹣18)2+1936,
∴当x=18时,w取得最大值,最大利润为1936元;
综上,在销售的第18天时,当天的利润最大,最大利润是1936元;
(3)当1≤x≤7时,168x+672≥1680,
解得x≥6,
∴此时满足条件的天数为第6、7这2天;
当8≤x≤20时,﹣4(x﹣18)2+1936≥1680,
解得10≤x≤26,
又∵x≤20,
∴10≤x≤20,
∴此时满足条件的天数有11天;
综上,试销的20天中当天的销售利润不低于1680元的有13天.
24.(12分)抛物线l1:y=x2+bx+c与它的对称轴x=﹣2交于点A,且经过点B(0,﹣2).
(1)求抛物线l1的解析式;
(2)如图1,直线y=kx+2k﹣8(k<0)与抛物线l1交于点E,F,若△AEF的面积为,求k的值;
(3)如图2,将抛物线l1向下平移n(n>0)个单位长度得到抛物线l2,抛物线l2与y轴交于点C,过点C作x轴的平行线交抛物线l2于另一点D;抛物线l2的对称轴与x轴的交于点M,P为线段OC上一点,若△POM与△PCD相似,并且符合该条件的点P有且只有2个,求n的值及相应点P的坐标.
解:(1)根据题意有,
解得,
∴抛物线l1的解析式为y=x2+4x﹣2.
(2)如图1,设直线y=kx+2k﹣8与抛物线l1的对称轴交点为G,则G(﹣2,﹣8),
又可得抛物线l1的顶点A(﹣2,﹣6),
∴AG=2,
S△AEF=S△AGE﹣S△AGF
=AG?(﹣2﹣xE)﹣AG?(﹣2﹣xF)
=AG?(xF﹣xE),
又∵S△AEF=2,AG=2,
∴xF﹣xE=2,
将抛物线l1与直线y=kx+2k﹣8联立得,
消去y得x2+4x﹣2=kx+2k﹣8,
整理得x2+(4﹣k)x﹣2k+6=0,得x=,
∴xF﹣xE=,
∴=2,
解得k=±4,
又k<0,
∴k=﹣4.
(3)设抛物线l2的解析式为y=x2+4x﹣2﹣m,
∴C(0,﹣2﹣n),D(﹣4,﹣2﹣n),M(﹣2,0)
设P(0,t).
①当△PCD∽△MOP时,=,
∴=,
∴t2+(n+2)t+8=0;
②当△PCD∽△POM时,=,
∴=,
∴t=﹣;
(Ⅰ)当方程①有两个相等实数根时,
△=(n+2)2﹣4×1×8=0,
解得n=±4﹣2,
又n>0,
∴n=4﹣2,
此时方程①有两个相等实根t1=t2=﹣2,方程②有一个实数根t=﹣;
∴n=4﹣2,
此时点P的坐标为(0,﹣2)和(0,﹣);
(Ⅱ)当方程①有两个不相等的实数根时,
把②代入①,得:﹣+8=0,即(n+2)2=36,
解得n1=4,n2=﹣8,
又n>0,
∴n=4,
此时方程①有两个不相等的实数根,t1=﹣2,t2=﹣4,方程①有一个实数根t=﹣2;
∴n=4,
此时点P坐标为(0,﹣2)和(0,﹣4),
综上,当n=4﹣2时,点P的坐标为(0,﹣2)和(0,﹣);当n=4时,点P坐标为(0,﹣2)和(0,﹣4).
同课章节目录
