初中数学鲁教版七年级上册第三章勾股定理测试题(Word版含解析)
文档属性
| 名称 | 初中数学鲁教版七年级上册第三章勾股定理测试题(Word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 204.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-19 00:00:00 | ||
图片预览



文档简介
初中数学鲁教版七年级上册第三章勾股定理测试题
一、选择题
已知三角形三边的长分别为3、2、,则该三角形的形状是
A.
锐角三角形
B.
直角三角形
C.
钝角三角形
D.
无法确定
下列长度的三条线段能组成直角三角形的是
A.
5,11,12
B.
3,4,5
C.
4,6,8
D.
6,12,13
已知的三边为a,b,c,下列条件不能判定为直角三角形的是
A.
,,
B.
,,
C.
,,
D.
,,;
如图,已知圆柱的底面直径,高,小虫在圆柱表面爬行,从C点爬到A点,然后再沿另一面爬回C点,则小虫爬行的最短路程为
A.
B.
C.
D.
如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块可重复选取按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是
A.
1,4,5
B.
2,3,5
C.
3,4,5
D.
2,2,4
下列各组数据不是勾股数的是
A.
2,3,4
B.
3,4,5
C.
5,12,13
D.
6,8,10
如图,正方体的棱长为4cm,A是正方体的一个顶点,B是侧面正方形对角线的交点.一只蚂蚁在正方体的表面上爬行,从点A爬到点B的最短路径是
A.
9
B.
C.
D.
12
如图,一个长方体的长宽高分别是6米、3米、2米,一只蚂蚁沿长方体的表面从点A到点所经过的最短路线长为???????
A.
?
B.
?
C.
D.
以上都不对
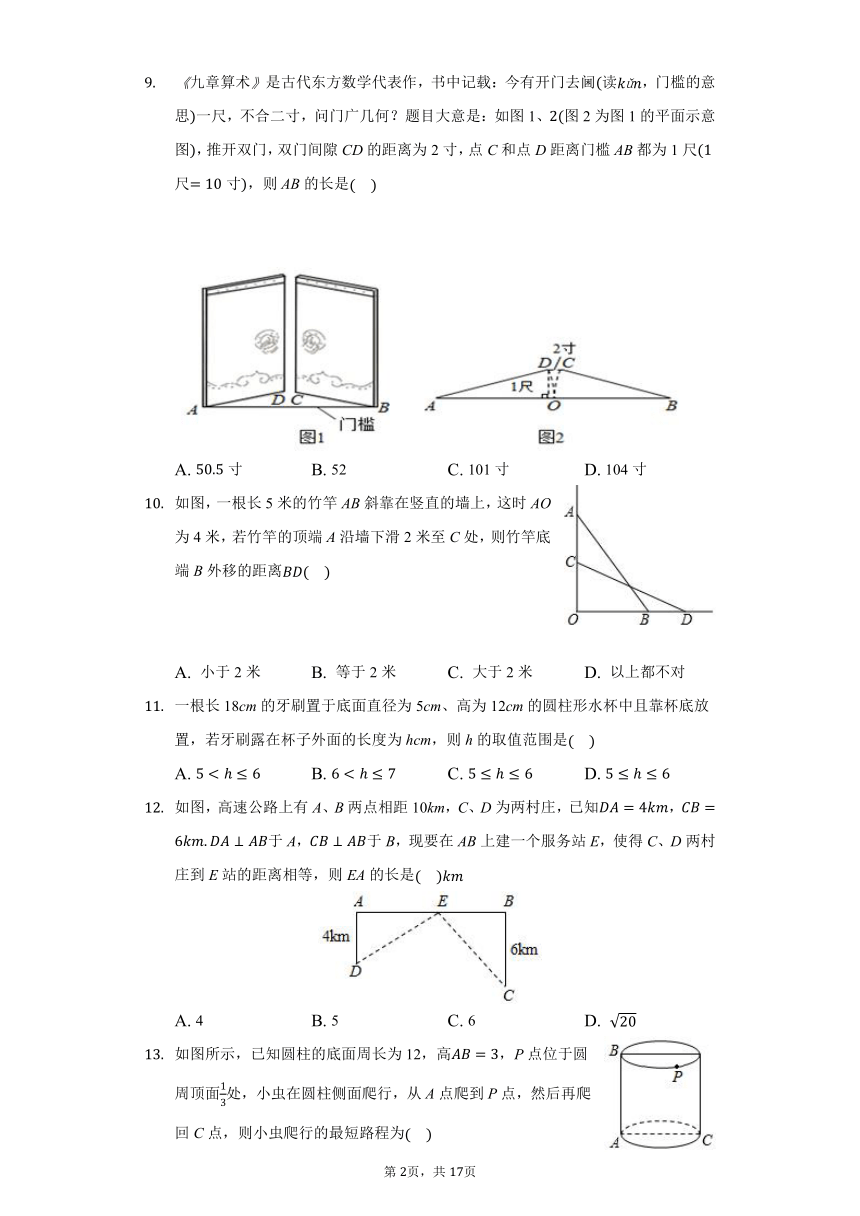
九章算术是古代东方数学代表作,书中记载:今有开门去阃读,门槛的意思一尺,不合二寸,问门广几何?题目大意是:如图1、图2为图1的平面示意图,推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺尺寸,则AB的长是
A.
寸
B.
52
C.
101寸
D.
104寸
如图,一根长5米的竹竿AB斜靠在竖直的墙上,这时AO为4米,若竹竿的顶端A沿墙下滑2米至C处,则竹竿底端B外移的距离
A.
小于2米
B.
等于2米
C.
大于2米
D.
以上都不对
一根长18cm的牙刷置于底面直径为5cm、高为12cm的圆柱形水杯中且靠杯底放置,若牙刷露在杯子外面的长度为hcm,则h的取值范围是
A.
B.
C.
D.
如图,高速公路上有A、B两点相距10km,C、D为两村庄,已知,于A,于B,现要在AB上建一个服务站E,使得C、D两村庄到E站的距离相等,则EA的长是
A.
4
B.
5
C.
6
D.
如图所示,已知圆柱的底面周长为12,高,P点位于圆周顶面处,小虫在圆柱侧面爬行,从A点爬到P点,然后再爬回C点,则小虫爬行的最短路程为
A.
B.
10
C.
D.
如图,在波平如镜的湖面上,有一朵盛开的美丽的红莲,它高出水面突然一阵大风吹过,红莲被吹至一边,花朵下部刚好齐及水面,如果知道红莲移动的水平距离为60cm,则水深是.
A.
35
B.
40
C.
50
D.
45
二、填空题
如图,以的三边为斜边,向外作等腰直角三角形,其面积分别是,,,且,,当______时,.
与5、13组成勾股数的第三个数有______个.
如图,长方体的长为15厘米,宽为10厘米,高为20厘米,点B到点C的距离是5厘米.一只小虫在长方体表面从A爬到B的最短路程是______.
如图,将一根长为的橡皮筋水平放置在桌面上,固定两端A和B,然后把中点C竖直地向上拉升3cm至D点,则拉长后橡皮筋的长度为______cm.
“折竹抵地”问题源自九章算术中,即:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远,则折断后的竹子高度为______尺.
三、计算题
张老师在一次“探究性学习”课中,设计了如下数表:
n
2
3
4
5
a
b
4
6
8
10
c
请你分别观察a、b、c与n之间的关系,并用含自然数n?的代数式表示;
猜想:以a、b、c为边的三角形是否为直角三角形?请证明你的猜想.
如图所示,某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道a上确定点D,使,测得米,在a上点D的同侧取点A、B,使,.
求AB的长结果保留根号;
已知本路段对汽车限速为60千米小时,若测得某汽车从A到B用时2秒,这辆汽车是否超速?说明理由.参考数据:
“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上的行驶速度不得超过70千米时.一辆“小汽车”在一条城市街路上直道行驶,某一时刻刚好行驶到路对面“车速检测仪A”正前方50米C处,过了6秒后,测得“小汽车”位置B与“车速检测仪A”之间的距离为130米,这辆“小汽车”超速了吗?请说明理由.
四、解答题
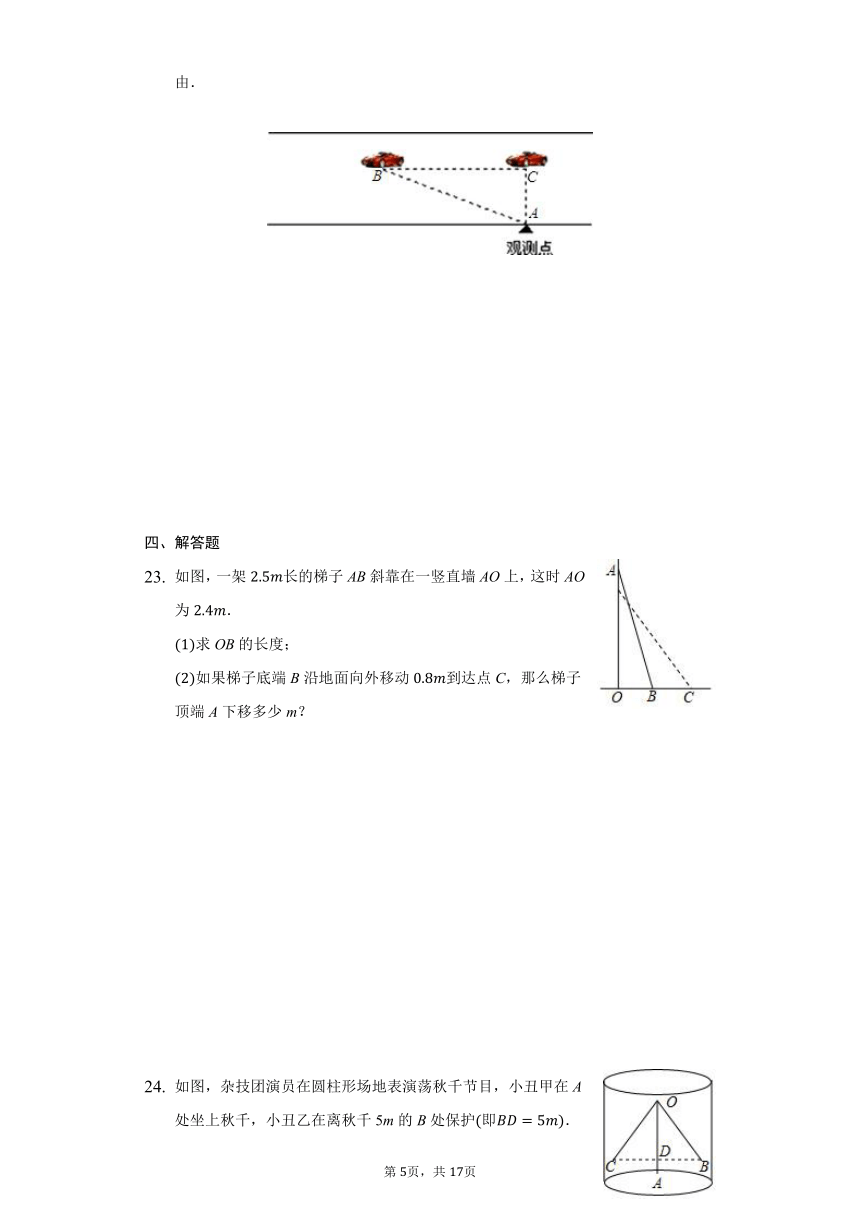
如图,一架长的梯子AB斜靠在一竖直墙AO上,这时AO为.
求OB的长度;
如果梯子底端B沿地面向外移动到达点C,那么梯子顶端A下移多少m?
如图,杂技团演员在圆柱形场地表演荡秋千节目,小丑甲在A处坐上秋千,小丑乙在离秋千5m的B处保护即.
当甲荡至乙处时,乙发现甲升高了1m,于是他就算出了秋千绳索的长度,你知道他是怎么算的吗?请你试一试.
为了保证表演的安全性,要求秋千最大幅度的张角不能超过张角指的是秋千绳索和铅垂方向的夹角,在小题绳索长度不变的情况下,那么圆柱形场地的底面直径至少应该是多少米?
答案和解析
1.【答案】B
【解析】解:,
该三角形是直角三角形,
故选:B.
两小边的平方和等于最长边的平方,即可由勾股定理的逆定理证明三角形是直角三角形.
本题考查勾股定理的逆定理:如果三角形的三边长a,b,c满足,那么这个三角形就是直角三角形.知道三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.
2.【答案】B
【解析】
【分析】
此题考查勾股定理逆定理的运用,属于基础题.
根据勾股定理的逆定理进行判断,如果三角形两条边的平方和等于第三边的平方,那么这个三角形就是直角三角形.
【解答】
解:A、因为,所以三条线段不能组成直角三角形;
B、因为,所以三条线段能组成直角三角形;
C、因为,所以三条线段不能组成直角三角形;
D、因为,所以三条线段不能组成直角三角形.
故选B.
3.【答案】D
【解析】解:A、,该三角形符合勾股定理的逆定理,故是直角三角形,故选项不符合题意;
B、,该三角形符合勾股定理的逆定理,故是直角三角形,故选项不符合题意;
C、,该三角形符合勾股定理的逆定理,故是直角三角形,故选项不符合题意;
D、,该三角形不符合勾股定理的逆定理,故不是直角三角形,故选项符合题意;
故选:D.
根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个是直角三角形判定则可.如果有这种关系,这个就是直角三角形.
本题考查了勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.
4.【答案】D
【解析】解:把圆柱侧面展开,展开图如右图所示,点A、C的最短距离为线段AC的长.
在中,,,AD为底面半圆弧长,,
所以,
从C点爬到A点,然后再沿另一面爬回C点,则小虫爬行的最短路程为,
故选:D.
要求最短路径,首先要把圆柱的侧面展开,利用两点之间线段最短,然后利用勾股定理即可求解.
本题考查了平面展开最短路径问题,解题的关键是会将圆柱的侧面展开,并利用勾股定理解答.
5.【答案】B
【解析】解:当选取的三块纸片的面积分别是1,4,5时,围成的直角三角形的面积是,
当选取的三块纸片的面积分别是2,3,5时,围成的直角三角形的面积是;
当选取的三块纸片的面积分别是3,4,5时,围成的三角形不是直角三角形;
当选取的三块纸片的面积分别是2,2,4时,围成的直角三角形的面积是,
,
所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是2,3,5,
故选:B.
根据题意可知,三块三角形的面积中,两个较小的面积之和等于最大的面积,再根据三角形的面积,分别计算出各个选项中围成的直角三角形的面积,比较大小,即可解答本题.
本题考查勾股定理的逆定理,解答本题的关键是明确题意,利用勾股定理的逆定理解答.
6.【答案】A
【解析】解:A、,不能构成直角三角形,所以不是勾股数,故符合题意;
B、,能构成直角三角形,所以是勾股数,故不符合题意;
C、,能构成直角三角形,所以是勾股数,故不符合题意;
D、,能构成直角三角形,所以是勾股数,故不符合题意;
故选:A.
欲判断是否为勾股数,必须根据勾股数是正整数,同时还需验证两小边的平方和是否等于最长边的平方.
此题主要考查了勾股数的定义,及勾股定理的逆定理:已知的三边满足,则是直角三角形.
7.【答案】C
【解析】解:如图,,
故选:C.
将正方体的左侧面与前面展开,构成一个长方形,用勾股定理求出距离即可.
本题考查了最短路径问题,勾股定理,解题的关键是将平面展开,组成一个直角三角形.
8.【答案】C
【解析】
【分析】
此题考查平面的最短路径问题,关键是把长方体拉平后用了勾股定理求出对角线的长度.蚂蚁有三种爬法,就是把正视和俯视或正视和侧视,或俯视和侧视二个面展平成一个长方形,然后求其对角线,比较大小即可求得最短的途径.
【解答】
解:如图所示,
路径一:;
路径二:;
路径三:;
,
为最短路径.
故选:C.
9.【答案】C
【解析】
【分析】
本题考查了勾股定理的应用,弄懂题意,构建直角三角形是解题的关键.画出直角三角形,根据勾股
定理即可得到结论.
【解答】
解:过D作于E,如图2所示:
由题意得:,
设,
则,,,,
在中,
,即,
解得:,
寸,
寸,
故选:C.
10.【答案】A
【解析】解:由题意得:在中,米,米,
米,
在中,米,米,
米,
米.
故选:A.
要求下滑的距离,显然需要分别放到两个直角三角形中,运用勾股定理求得BO和DO的长即可.
本题考查了勾股定理的应用,注意此题中竹竿的长度是不变的.熟练运用勾股定理是解题的关键.
11.【答案】C
【解析】解:将一根长为18cm的牙刷,置于底面直径为5cm,高为12cm的圆柱形水杯中,
在杯子中牙刷最短是等于杯子的高,最长是等于杯子斜边长度,
当杯子中牙刷最短是等于杯子的高时,,
最长时等于牙刷斜边长度是:,
的取值范围是:,
即.
故选:C.
根据杯子内牙刷的长度取值范围得出杯子外面长度的取值范围,即可得出答案.
此题主要考查了勾股定理的应用,正确得出杯子内牙刷的取值范围是解决问题的关键.
12.【答案】C
【解析】解:设,则,
由勾股定理得:
在中,
,
在中,
,
由题意可知:,
所以:,
解得:.
所以,EB的长是4km.
所以,.
故选:C.
根据题意设出BE的长为xkm,再由勾股定理列出方程求解即可.
本题考查了勾股定理的应用,熟练掌握勾股定理是本题的关键.
13.【答案】C
【解析】解:如图,小虫爬行的最短路程,
故选:C.
先将图形展开,再根据两点之间线段最短,由勾股定理可得出.
此题主要考查了平面展开图最短路径问题,此矩形的长等于圆柱底面周长,矩形的宽即高等于圆柱的母线长.本题就是把圆柱的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.
14.【答案】D
【解析】解:红莲被吹至一边,花朵刚好齐及水面即AC为红莲的长.
设水深h尺,由题意得:
中,,,,
由勾股定理得:,
即,
解得:.
故选:D.
仔细分析该题,可画出草图,关键是水深、红莲移动的水平距离及红莲的高度构成一直角三角形,解此直角三角形即可.
本题考查正确运用勾股定理,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.
15.【答案】9
【解析】解:当时,以的三边为斜边,向外作等腰直角三角形,
可得:,
,
故答案为:9
根据勾股定理的逆定理解答即可.
本题主要考查了等腰直角三角形及勾股定理,解题的关键是求出,,式子.
16.【答案】1
【解析】解:当5,13为两条直角边时,则斜边为:,
不是整数,故5,13,不是勾股数;
当13为斜边时,则另一条直角边是:,
故5,12,13是勾股数,
故答案为:1.
根据勾股定理和勾股数的定义,可以得到第三个数,然后即可得到与5、13组成勾股数的第三个数有几个.
本题考查勾股数,解答本题的关键是明确题意,利用勾股定理解答.
17.【答案】25厘米
【解析】解:只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形,如第1个图:
长方体的宽为10cm,高为20cm,点B离点C的距离是5,
,,
在直角三角形ABD中,根据勾股定理得:
;
只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如第2个图:
长方体的宽为10cm,高为20cm,点B离点C的距离是5,
,,
在直角三角形ABD中,根据勾股定理得:
;
只要把长方体的右侧表面剪开与后面这个侧面所在的平面形成一个长方形,如第3个图:
长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,
,
在直角三角形ABC中,根据勾股定理得:
;
,
自A至B在长方体表面的连线距离最短是25cm.
故答案为:25厘米
求长方体中两点之间的最短路径,最直接的作法,就是将长方体侧面展开,然后利用两点之间线段最短解答.
此题主要考查平面展开图的最短距离,注意长方体展开图的不同情况,正确利用勾股定理解决问题.
18.【答案】10
【解析】解:中,,;
根据勾股定理,得:;
同理可得,
;
故拉长后橡皮筋的长度为10cm.
故答案为:10.
根据勾股定理,可求出AD、BD的长,则即为橡皮筋拉长后的距离.
此题主要考查了等腰三角形的性质以及勾股定理的应用.在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.
19.【答案】
【解析】解:设折断处离地面的高度OA是x尺,根据题意可得:
,
解得:,
答:折断处离地面的高度OA是尺.
故答案为:.
根据题意结合勾股定理得出折断处离地面的长度即可.
此题主要考查了勾股定理的应用,根据题意正确应用勾股定理是解题关键.
20.【答案】解:由图表可以得出:
时,,,,
时,,,,
时,,,,
,,.
、b、c为边的三角形时:
,
,
,
以a、b、c为边的三角形是直角三角形.
【解析】利用图表可以发现a,b,c与n的关系,a与c正好是,加减1,即可得出答案;
利用完全平方公式计算出的值,以及的值,再利用勾股定理逆定理即可求出.
此题主要考查了勾股定理逆定理与数字的变化规律等知识,利用图表之间的变化得出a、b、c与n之间的关系是解决问题的关键.
21.【答案】解:在中,米,,
米,
在在中,米,,
米,
米;
汽车行驶车速,
,
这辆车没有超速.
【解析】在中求出AD,在中求出BD,继而可得出AB的长度;
根据速度路程时间,求出速度,继而比较可判断是否超速.
本题考查了勾股定理的应用及直角三角形的应用,解答本题的关键是仔细审题,熟练掌握锐角三角函数的定义.
22.【答案】解:由题意知,米,米,
且在中,AB是斜边,
根据勾股定理,
可以求得:米千米,
且6秒时,
所以速度为千米时,
故该小汽车超速.
答:该小汽车超速了,平均速度大于70千米时.
【解析】由题意知,为直角三角形,且AB是斜边,已知AB,AC根据勾股定理可以求BC,根据BC的长度和时间可以求小汽车在BC路程中的速度,若速度大于70千米时,则小汽车超速;若速度小于70千米时,则小汽车没有超速.
本题考查了勾股定理在实际生活中的应用,本题中准确的求出BC的长度,并计算小汽车的行驶速度是解题的关键.
23.【答案】解:在中,;
设梯子的A端下滑到D,如图,
,
在中,,
,
梯子顶端A下移.
【解析】根据勾股定理即可得到结论;
设梯子的A端下滑到D,如图,求得,根据勾股定理即可得到结论.
本题考查了勾股定理的应用,解答本题的关键是两次运用勾股定理,注意掌握勾股定理的表达式.
24.【答案】解:如图,连接设.
在中,,
,
,
答:秋千绳索的长度为13m.
由题意,在中,,,,
,
,
,,
,
,
答:圆柱形场地的底面直径至少应该是
【解析】如图,连接设在中,根据,构建方程即可解决问题.
由题意,是等腰直角三角形,根据等腰直角三角形的性质,求出BD即可解决问题.
本题考查勾股定理的应用,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.
第2页,共18页
第1页,共18页
一、选择题
已知三角形三边的长分别为3、2、,则该三角形的形状是
A.
锐角三角形
B.
直角三角形
C.
钝角三角形
D.
无法确定
下列长度的三条线段能组成直角三角形的是
A.
5,11,12
B.
3,4,5
C.
4,6,8
D.
6,12,13
已知的三边为a,b,c,下列条件不能判定为直角三角形的是
A.
,,
B.
,,
C.
,,
D.
,,;
如图,已知圆柱的底面直径,高,小虫在圆柱表面爬行,从C点爬到A点,然后再沿另一面爬回C点,则小虫爬行的最短路程为
A.
B.
C.
D.
如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块可重复选取按图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是
A.
1,4,5
B.
2,3,5
C.
3,4,5
D.
2,2,4
下列各组数据不是勾股数的是
A.
2,3,4
B.
3,4,5
C.
5,12,13
D.
6,8,10
如图,正方体的棱长为4cm,A是正方体的一个顶点,B是侧面正方形对角线的交点.一只蚂蚁在正方体的表面上爬行,从点A爬到点B的最短路径是
A.
9
B.
C.
D.
12
如图,一个长方体的长宽高分别是6米、3米、2米,一只蚂蚁沿长方体的表面从点A到点所经过的最短路线长为???????
A.
?
B.
?
C.
D.
以上都不对
九章算术是古代东方数学代表作,书中记载:今有开门去阃读,门槛的意思一尺,不合二寸,问门广几何?题目大意是:如图1、图2为图1的平面示意图,推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺尺寸,则AB的长是
A.
寸
B.
52
C.
101寸
D.
104寸
如图,一根长5米的竹竿AB斜靠在竖直的墙上,这时AO为4米,若竹竿的顶端A沿墙下滑2米至C处,则竹竿底端B外移的距离
A.
小于2米
B.
等于2米
C.
大于2米
D.
以上都不对
一根长18cm的牙刷置于底面直径为5cm、高为12cm的圆柱形水杯中且靠杯底放置,若牙刷露在杯子外面的长度为hcm,则h的取值范围是
A.
B.
C.
D.
如图,高速公路上有A、B两点相距10km,C、D为两村庄,已知,于A,于B,现要在AB上建一个服务站E,使得C、D两村庄到E站的距离相等,则EA的长是
A.
4
B.
5
C.
6
D.
如图所示,已知圆柱的底面周长为12,高,P点位于圆周顶面处,小虫在圆柱侧面爬行,从A点爬到P点,然后再爬回C点,则小虫爬行的最短路程为
A.
B.
10
C.
D.
如图,在波平如镜的湖面上,有一朵盛开的美丽的红莲,它高出水面突然一阵大风吹过,红莲被吹至一边,花朵下部刚好齐及水面,如果知道红莲移动的水平距离为60cm,则水深是.
A.
35
B.
40
C.
50
D.
45
二、填空题
如图,以的三边为斜边,向外作等腰直角三角形,其面积分别是,,,且,,当______时,.
与5、13组成勾股数的第三个数有______个.
如图,长方体的长为15厘米,宽为10厘米,高为20厘米,点B到点C的距离是5厘米.一只小虫在长方体表面从A爬到B的最短路程是______.
如图,将一根长为的橡皮筋水平放置在桌面上,固定两端A和B,然后把中点C竖直地向上拉升3cm至D点,则拉长后橡皮筋的长度为______cm.
“折竹抵地”问题源自九章算术中,即:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远,则折断后的竹子高度为______尺.
三、计算题
张老师在一次“探究性学习”课中,设计了如下数表:
n
2
3
4
5
a
b
4
6
8
10
c
请你分别观察a、b、c与n之间的关系,并用含自然数n?的代数式表示;
猜想:以a、b、c为边的三角形是否为直角三角形?请证明你的猜想.
如图所示,某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道a上确定点D,使,测得米,在a上点D的同侧取点A、B,使,.
求AB的长结果保留根号;
已知本路段对汽车限速为60千米小时,若测得某汽车从A到B用时2秒,这辆汽车是否超速?说明理由.参考数据:
“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上的行驶速度不得超过70千米时.一辆“小汽车”在一条城市街路上直道行驶,某一时刻刚好行驶到路对面“车速检测仪A”正前方50米C处,过了6秒后,测得“小汽车”位置B与“车速检测仪A”之间的距离为130米,这辆“小汽车”超速了吗?请说明理由.
四、解答题
如图,一架长的梯子AB斜靠在一竖直墙AO上,这时AO为.
求OB的长度;
如果梯子底端B沿地面向外移动到达点C,那么梯子顶端A下移多少m?
如图,杂技团演员在圆柱形场地表演荡秋千节目,小丑甲在A处坐上秋千,小丑乙在离秋千5m的B处保护即.
当甲荡至乙处时,乙发现甲升高了1m,于是他就算出了秋千绳索的长度,你知道他是怎么算的吗?请你试一试.
为了保证表演的安全性,要求秋千最大幅度的张角不能超过张角指的是秋千绳索和铅垂方向的夹角,在小题绳索长度不变的情况下,那么圆柱形场地的底面直径至少应该是多少米?
答案和解析
1.【答案】B
【解析】解:,
该三角形是直角三角形,
故选:B.
两小边的平方和等于最长边的平方,即可由勾股定理的逆定理证明三角形是直角三角形.
本题考查勾股定理的逆定理:如果三角形的三边长a,b,c满足,那么这个三角形就是直角三角形.知道三条边的大小,用较小的两条边的平方和与最大的边的平方比较,如果相等,则三角形为直角三角形;否则不是.
2.【答案】B
【解析】
【分析】
此题考查勾股定理逆定理的运用,属于基础题.
根据勾股定理的逆定理进行判断,如果三角形两条边的平方和等于第三边的平方,那么这个三角形就是直角三角形.
【解答】
解:A、因为,所以三条线段不能组成直角三角形;
B、因为,所以三条线段能组成直角三角形;
C、因为,所以三条线段不能组成直角三角形;
D、因为,所以三条线段不能组成直角三角形.
故选B.
3.【答案】D
【解析】解:A、,该三角形符合勾股定理的逆定理,故是直角三角形,故选项不符合题意;
B、,该三角形符合勾股定理的逆定理,故是直角三角形,故选项不符合题意;
C、,该三角形符合勾股定理的逆定理,故是直角三角形,故选项不符合题意;
D、,该三角形不符合勾股定理的逆定理,故不是直角三角形,故选项符合题意;
故选:D.
根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个是直角三角形判定则可.如果有这种关系,这个就是直角三角形.
本题考查了勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.
4.【答案】D
【解析】解:把圆柱侧面展开,展开图如右图所示,点A、C的最短距离为线段AC的长.
在中,,,AD为底面半圆弧长,,
所以,
从C点爬到A点,然后再沿另一面爬回C点,则小虫爬行的最短路程为,
故选:D.
要求最短路径,首先要把圆柱的侧面展开,利用两点之间线段最短,然后利用勾股定理即可求解.
本题考查了平面展开最短路径问题,解题的关键是会将圆柱的侧面展开,并利用勾股定理解答.
5.【答案】B
【解析】解:当选取的三块纸片的面积分别是1,4,5时,围成的直角三角形的面积是,
当选取的三块纸片的面积分别是2,3,5时,围成的直角三角形的面积是;
当选取的三块纸片的面积分别是3,4,5时,围成的三角形不是直角三角形;
当选取的三块纸片的面积分别是2,2,4时,围成的直角三角形的面积是,
,
所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是2,3,5,
故选:B.
根据题意可知,三块三角形的面积中,两个较小的面积之和等于最大的面积,再根据三角形的面积,分别计算出各个选项中围成的直角三角形的面积,比较大小,即可解答本题.
本题考查勾股定理的逆定理,解答本题的关键是明确题意,利用勾股定理的逆定理解答.
6.【答案】A
【解析】解:A、,不能构成直角三角形,所以不是勾股数,故符合题意;
B、,能构成直角三角形,所以是勾股数,故不符合题意;
C、,能构成直角三角形,所以是勾股数,故不符合题意;
D、,能构成直角三角形,所以是勾股数,故不符合题意;
故选:A.
欲判断是否为勾股数,必须根据勾股数是正整数,同时还需验证两小边的平方和是否等于最长边的平方.
此题主要考查了勾股数的定义,及勾股定理的逆定理:已知的三边满足,则是直角三角形.
7.【答案】C
【解析】解:如图,,
故选:C.
将正方体的左侧面与前面展开,构成一个长方形,用勾股定理求出距离即可.
本题考查了最短路径问题,勾股定理,解题的关键是将平面展开,组成一个直角三角形.
8.【答案】C
【解析】
【分析】
此题考查平面的最短路径问题,关键是把长方体拉平后用了勾股定理求出对角线的长度.蚂蚁有三种爬法,就是把正视和俯视或正视和侧视,或俯视和侧视二个面展平成一个长方形,然后求其对角线,比较大小即可求得最短的途径.
【解答】
解:如图所示,
路径一:;
路径二:;
路径三:;
,
为最短路径.
故选:C.
9.【答案】C
【解析】
【分析】
本题考查了勾股定理的应用,弄懂题意,构建直角三角形是解题的关键.画出直角三角形,根据勾股
定理即可得到结论.
【解答】
解:过D作于E,如图2所示:
由题意得:,
设,
则,,,,
在中,
,即,
解得:,
寸,
寸,
故选:C.
10.【答案】A
【解析】解:由题意得:在中,米,米,
米,
在中,米,米,
米,
米.
故选:A.
要求下滑的距离,显然需要分别放到两个直角三角形中,运用勾股定理求得BO和DO的长即可.
本题考查了勾股定理的应用,注意此题中竹竿的长度是不变的.熟练运用勾股定理是解题的关键.
11.【答案】C
【解析】解:将一根长为18cm的牙刷,置于底面直径为5cm,高为12cm的圆柱形水杯中,
在杯子中牙刷最短是等于杯子的高,最长是等于杯子斜边长度,
当杯子中牙刷最短是等于杯子的高时,,
最长时等于牙刷斜边长度是:,
的取值范围是:,
即.
故选:C.
根据杯子内牙刷的长度取值范围得出杯子外面长度的取值范围,即可得出答案.
此题主要考查了勾股定理的应用,正确得出杯子内牙刷的取值范围是解决问题的关键.
12.【答案】C
【解析】解:设,则,
由勾股定理得:
在中,
,
在中,
,
由题意可知:,
所以:,
解得:.
所以,EB的长是4km.
所以,.
故选:C.
根据题意设出BE的长为xkm,再由勾股定理列出方程求解即可.
本题考查了勾股定理的应用,熟练掌握勾股定理是本题的关键.
13.【答案】C
【解析】解:如图,小虫爬行的最短路程,
故选:C.
先将图形展开,再根据两点之间线段最短,由勾股定理可得出.
此题主要考查了平面展开图最短路径问题,此矩形的长等于圆柱底面周长,矩形的宽即高等于圆柱的母线长.本题就是把圆柱的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.
14.【答案】D
【解析】解:红莲被吹至一边,花朵刚好齐及水面即AC为红莲的长.
设水深h尺,由题意得:
中,,,,
由勾股定理得:,
即,
解得:.
故选:D.
仔细分析该题,可画出草图,关键是水深、红莲移动的水平距离及红莲的高度构成一直角三角形,解此直角三角形即可.
本题考查正确运用勾股定理,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.
15.【答案】9
【解析】解:当时,以的三边为斜边,向外作等腰直角三角形,
可得:,
,
故答案为:9
根据勾股定理的逆定理解答即可.
本题主要考查了等腰直角三角形及勾股定理,解题的关键是求出,,式子.
16.【答案】1
【解析】解:当5,13为两条直角边时,则斜边为:,
不是整数,故5,13,不是勾股数;
当13为斜边时,则另一条直角边是:,
故5,12,13是勾股数,
故答案为:1.
根据勾股定理和勾股数的定义,可以得到第三个数,然后即可得到与5、13组成勾股数的第三个数有几个.
本题考查勾股数,解答本题的关键是明确题意,利用勾股定理解答.
17.【答案】25厘米
【解析】解:只要把长方体的右侧表面剪开与前面这个侧面所在的平面形成一个长方形,如第1个图:
长方体的宽为10cm,高为20cm,点B离点C的距离是5,
,,
在直角三角形ABD中,根据勾股定理得:
;
只要把长方体的右侧表面剪开与上面这个侧面所在的平面形成一个长方形,如第2个图:
长方体的宽为10cm,高为20cm,点B离点C的距离是5,
,,
在直角三角形ABD中,根据勾股定理得:
;
只要把长方体的右侧表面剪开与后面这个侧面所在的平面形成一个长方形,如第3个图:
长方体的宽为10cm,高为20cm,点B离点C的距离是5cm,
,
在直角三角形ABC中,根据勾股定理得:
;
,
自A至B在长方体表面的连线距离最短是25cm.
故答案为:25厘米
求长方体中两点之间的最短路径,最直接的作法,就是将长方体侧面展开,然后利用两点之间线段最短解答.
此题主要考查平面展开图的最短距离,注意长方体展开图的不同情况,正确利用勾股定理解决问题.
18.【答案】10
【解析】解:中,,;
根据勾股定理,得:;
同理可得,
;
故拉长后橡皮筋的长度为10cm.
故答案为:10.
根据勾股定理,可求出AD、BD的长,则即为橡皮筋拉长后的距离.
此题主要考查了等腰三角形的性质以及勾股定理的应用.在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.
19.【答案】
【解析】解:设折断处离地面的高度OA是x尺,根据题意可得:
,
解得:,
答:折断处离地面的高度OA是尺.
故答案为:.
根据题意结合勾股定理得出折断处离地面的长度即可.
此题主要考查了勾股定理的应用,根据题意正确应用勾股定理是解题关键.
20.【答案】解:由图表可以得出:
时,,,,
时,,,,
时,,,,
,,.
、b、c为边的三角形时:
,
,
,
以a、b、c为边的三角形是直角三角形.
【解析】利用图表可以发现a,b,c与n的关系,a与c正好是,加减1,即可得出答案;
利用完全平方公式计算出的值,以及的值,再利用勾股定理逆定理即可求出.
此题主要考查了勾股定理逆定理与数字的变化规律等知识,利用图表之间的变化得出a、b、c与n之间的关系是解决问题的关键.
21.【答案】解:在中,米,,
米,
在在中,米,,
米,
米;
汽车行驶车速,
,
这辆车没有超速.
【解析】在中求出AD,在中求出BD,继而可得出AB的长度;
根据速度路程时间,求出速度,继而比较可判断是否超速.
本题考查了勾股定理的应用及直角三角形的应用,解答本题的关键是仔细审题,熟练掌握锐角三角函数的定义.
22.【答案】解:由题意知,米,米,
且在中,AB是斜边,
根据勾股定理,
可以求得:米千米,
且6秒时,
所以速度为千米时,
故该小汽车超速.
答:该小汽车超速了,平均速度大于70千米时.
【解析】由题意知,为直角三角形,且AB是斜边,已知AB,AC根据勾股定理可以求BC,根据BC的长度和时间可以求小汽车在BC路程中的速度,若速度大于70千米时,则小汽车超速;若速度小于70千米时,则小汽车没有超速.
本题考查了勾股定理在实际生活中的应用,本题中准确的求出BC的长度,并计算小汽车的行驶速度是解题的关键.
23.【答案】解:在中,;
设梯子的A端下滑到D,如图,
,
在中,,
,
梯子顶端A下移.
【解析】根据勾股定理即可得到结论;
设梯子的A端下滑到D,如图,求得,根据勾股定理即可得到结论.
本题考查了勾股定理的应用,解答本题的关键是两次运用勾股定理,注意掌握勾股定理的表达式.
24.【答案】解:如图,连接设.
在中,,
,
,
答:秋千绳索的长度为13m.
由题意,在中,,,,
,
,
,,
,
,
答:圆柱形场地的底面直径至少应该是
【解析】如图,连接设在中,根据,构建方程即可解决问题.
由题意,是等腰直角三角形,根据等腰直角三角形的性质,求出BD即可解决问题.
本题考查勾股定理的应用,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.
第2页,共18页
第1页,共18页
