4.4.2 探索三角形相似的条件课件(共21张PPT)
文档属性
| 名称 | 4.4.2 探索三角形相似的条件课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-20 21:41:05 | ||
图片预览





文档简介
数学北师大版
九年级
4.4.2 探索三角形相似的条件
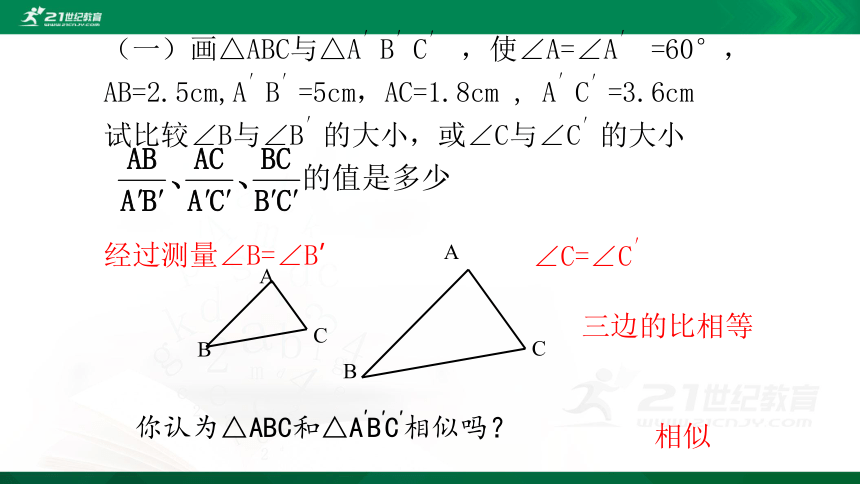
(一)画△ABC与△A′B′C′ ,使∠A=∠A′ =60°,AB=2.5cm,A′B′=5cm,AC=1.8cm , A′C′=3.6cm
试比较∠B与∠B′的大小,或∠C与∠C′的大小
你认为△ABC和△A′B′C′相似吗?
A
C
B
A
C
B
经过测量∠B=∠B’
∠C=∠C′
三边的比相等
相似
(二)画△ABC与△A′B′C′ ,使∠A=∠A′=45°, AB=2cm,A′B ′=3cm,AC=4cm , A′C′ =6cm
1.△ABC与△A′B′C′相似吗,为什么?
2.猜想:改变AB与A′B′、 AC与A′C′的比值,△ABC与△A′B′C′相似吗?
相似
相似
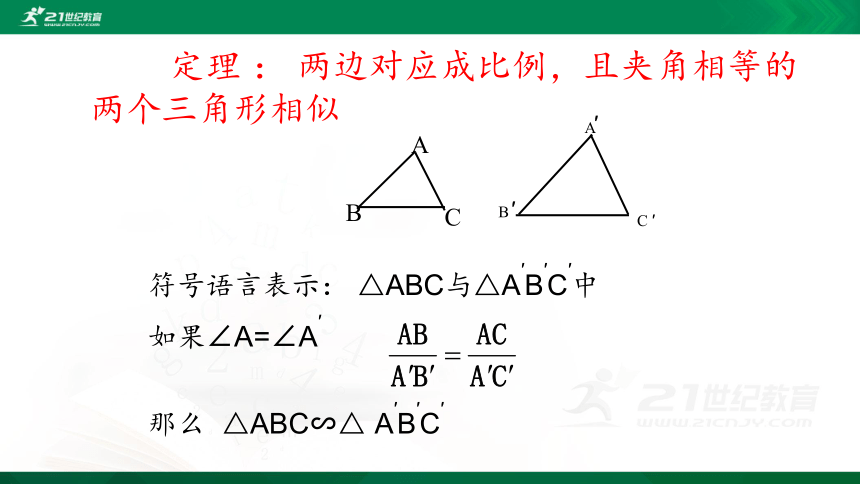
定理 : 两边对应成比例,且夹角相等的两个三角形相似
A
C
B
A
C ′
B
′
′
符号语言表示: △ABC与△A′B′C′中
如果∠A=∠A′
那么 △ABC∽△ A′B′C′
我们来证明一下前面得出的结论:
如图,在△ABC与△A′B′C′中,已知∠A= ∠A′,
证明:在 △A′B′C′ 的边 A′B′ 上截取点D,使 A′D = AB.过点 D 作 DE∥B′C′,交 A′C′ 于点 E.
∵ DE∥B′C′,∴ △A′DE∽△A′B′C′.
求证:△ABC∽△A′B′C′.
B
A
C
D
E
B'
A'
C'
∴
∵ A′D=AB,
∴
∴ A′E = AC . 又 ∠A′ = ∠A.
∴ △A′DE ≌ △ABC, ∴ △A′B′C′ ∽ △ABC.
例1.如图所示,D、E分别是△ABC的边AC、AB上的点.AE=1.5,AC=2,BC=3,且 ,求DE的长.
A
E
D
C
B
解:∵AE=1.5,AC=2
且∠EAD=∠CAB
∴△EAD∽△CAB(两边对应成比例且夹角相等的两个三角形相似)
又∵BC=3
∴DE
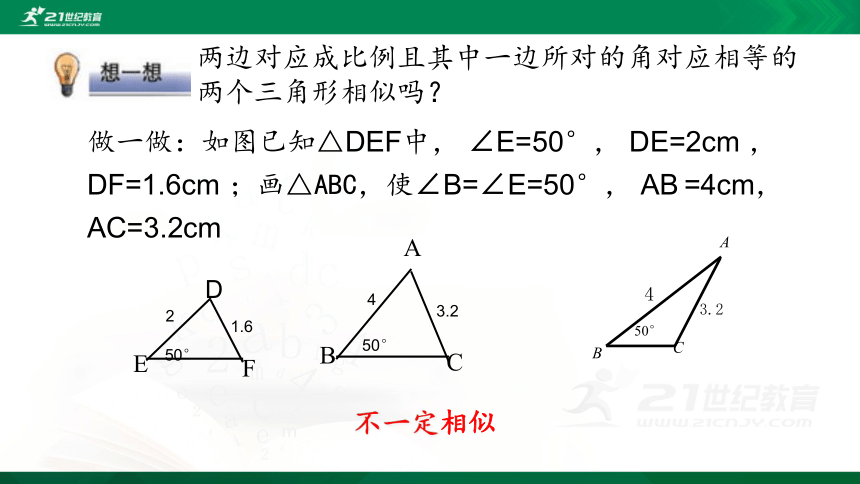
两边对应成比例且其中一边所对的角对应相等的两个三角形相似吗?
做一做:如图已知△DEF中, ∠E=50°, DE=2cm ,DF=1.6cm ;画△ABC,使∠B=∠E=50°, AB =4cm,AC=3.2cm
D
F
E
50°
2
1.6
A
C
B
50°
3.2
4
50°
4
A
B
C
3.2
不一定相似
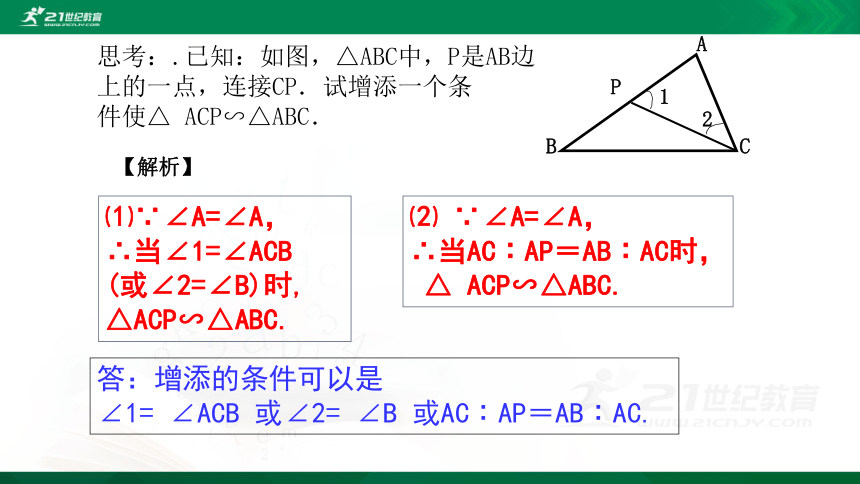
思考:.已知:如图,△ABC中,P是AB边
上的一点,连接CP.试增添一个条
件使△ ACP∽△ABC.
A
P
B
C
1
2
【解析】
⑴∵∠A=∠A,
∴当∠1=∠ACB
(或∠2=∠B)时,
△ACP∽△ABC.
⑵ ∵∠A=∠A,
∴当AC︰AP=AB︰AC时,
△ ACP∽△ABC.
答:增添的条件可以是
∠1= ∠ACB 或∠2= ∠B 或AC︰AP=AB︰AC.
例3 如图,在 △ABC 中,CD 是边 AB 上的高,且 ,求证 ∠ACB=90°.
A
B
C
D
证明: ∵ CD 是边 AB 上的高,
∴ ∠ADC =∠CDB =90°.
∵
∴△ADC ∽△CDB,∴ ∠ACD =∠B,
∴ ∠ACB =∠ACD +∠BCD =∠B +∠BCD = 90°.
解析:当 △ADP ∽△ACB 时,
AP : AB =AD : AC ,∴ AP : 12 =6 : 8 ,
解得 AP = 9;
当 △ADP ∽△ABC 时,
AD : AB =AP : AC ,∴ 6 : 12 = AP : 8 ,
解得 AP = 4.
∴ 当 AP 的长度为 4 或 9 时,
△ADP 和 △ABC 相似.
1. 如图,已知 △ABC中,D 为边 AC 上一点,P 为边
AB上一点,AB = 12,AC = 8,AD = 6,当 AP 的长
度为 时,△ADP 和 △ABC 相似.
A
B
C
D
4 或 9
P
P
提高训练
2.△ABC为锐角三角形,BD、CE为高 .
求证:△ ADE∽ △ ABC.
A
B
D
C
E
O
证明:∵BD⊥AC,CE⊥AB,
∴∠ABD+∠A=90°,
∠ACE+∠A= 90°.
∴ ∠ABD= ∠ACE.
又∵ ∠A= ∠A,
∴△ ABD ∽ △ ACE.
∴
∵ ∠A= ∠A,
∴ △ ADE ∽ △ ABC.
DE‖AB
∠B=∠AED
AB‖CD
∠A=∠C
∠BAC=900
AD⊥BC
∠BAD=∠C
本节归纳
作业布置:
习题4.6 1,2,3,4
选讲内容:
Rt△ABC中,AD⊥BC,
①AD2=BD.DC
②AB2=BD.BC
③AC2=DC.BC
射影定理
1.如图,直线EF分别交△ABC的边AC,AB于点E,F,交边BC的延长线于点D,且AB?BF= BC?BD.求证: AE?EC= EF?ED.
证明:∵AB·BFBC·=BD,
又∵∠B=∠B,
∴△ABC∽△DBF
又∵∠AEF=∠DEC,
即AE?EC= EF?ED.
∴∠A=∠D.
∴ .△AEF ∽△DEC
2.如图,在矩形ABCD中,AB=1,BC=2,点E在AD上,且ED=3AE.求证:△ABC∽△EAB.
3. 如图,在四边形 ABCD 中,已知 ∠B =∠ACD,
AB=6,BC=4,AC=5,CD= ,求 AD 的长.
A
B
C
D
解:∵AB=6,BC=4,AC=5,CD= ,
∴
又∵∠B=∠ACD,
∴ △ABC ∽ △DCA,
∴ ,
∴
4. 如图,∠DAB =∠CAE,且 AB · AD = AE·AC,求证
△ABC ∽△AED.
A
B
C
D
E
证明:∵ AB · AD = AE·AC,
∴
又∵ ∠DAB =∠CAE,
∴∠ DAB +∠BAE =∠CAE +∠BAE ,
即∠DAE =∠BAC,
∴ △ABC ∽△AED.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
九年级
4.4.2 探索三角形相似的条件
(一)画△ABC与△A′B′C′ ,使∠A=∠A′ =60°,AB=2.5cm,A′B′=5cm,AC=1.8cm , A′C′=3.6cm
试比较∠B与∠B′的大小,或∠C与∠C′的大小
你认为△ABC和△A′B′C′相似吗?
A
C
B
A
C
B
经过测量∠B=∠B’
∠C=∠C′
三边的比相等
相似
(二)画△ABC与△A′B′C′ ,使∠A=∠A′=45°, AB=2cm,A′B ′=3cm,AC=4cm , A′C′ =6cm
1.△ABC与△A′B′C′相似吗,为什么?
2.猜想:改变AB与A′B′、 AC与A′C′的比值,△ABC与△A′B′C′相似吗?
相似
相似
定理 : 两边对应成比例,且夹角相等的两个三角形相似
A
C
B
A
C ′
B
′
′
符号语言表示: △ABC与△A′B′C′中
如果∠A=∠A′
那么 △ABC∽△ A′B′C′
我们来证明一下前面得出的结论:
如图,在△ABC与△A′B′C′中,已知∠A= ∠A′,
证明:在 △A′B′C′ 的边 A′B′ 上截取点D,使 A′D = AB.过点 D 作 DE∥B′C′,交 A′C′ 于点 E.
∵ DE∥B′C′,∴ △A′DE∽△A′B′C′.
求证:△ABC∽△A′B′C′.
B
A
C
D
E
B'
A'
C'
∴
∵ A′D=AB,
∴
∴ A′E = AC . 又 ∠A′ = ∠A.
∴ △A′DE ≌ △ABC, ∴ △A′B′C′ ∽ △ABC.
例1.如图所示,D、E分别是△ABC的边AC、AB上的点.AE=1.5,AC=2,BC=3,且 ,求DE的长.
A
E
D
C
B
解:∵AE=1.5,AC=2
且∠EAD=∠CAB
∴△EAD∽△CAB(两边对应成比例且夹角相等的两个三角形相似)
又∵BC=3
∴DE
两边对应成比例且其中一边所对的角对应相等的两个三角形相似吗?
做一做:如图已知△DEF中, ∠E=50°, DE=2cm ,DF=1.6cm ;画△ABC,使∠B=∠E=50°, AB =4cm,AC=3.2cm
D
F
E
50°
2
1.6
A
C
B
50°
3.2
4
50°
4
A
B
C
3.2
不一定相似
思考:.已知:如图,△ABC中,P是AB边
上的一点,连接CP.试增添一个条
件使△ ACP∽△ABC.
A
P
B
C
1
2
【解析】
⑴∵∠A=∠A,
∴当∠1=∠ACB
(或∠2=∠B)时,
△ACP∽△ABC.
⑵ ∵∠A=∠A,
∴当AC︰AP=AB︰AC时,
△ ACP∽△ABC.
答:增添的条件可以是
∠1= ∠ACB 或∠2= ∠B 或AC︰AP=AB︰AC.
例3 如图,在 △ABC 中,CD 是边 AB 上的高,且 ,求证 ∠ACB=90°.
A
B
C
D
证明: ∵ CD 是边 AB 上的高,
∴ ∠ADC =∠CDB =90°.
∵
∴△ADC ∽△CDB,∴ ∠ACD =∠B,
∴ ∠ACB =∠ACD +∠BCD =∠B +∠BCD = 90°.
解析:当 △ADP ∽△ACB 时,
AP : AB =AD : AC ,∴ AP : 12 =6 : 8 ,
解得 AP = 9;
当 △ADP ∽△ABC 时,
AD : AB =AP : AC ,∴ 6 : 12 = AP : 8 ,
解得 AP = 4.
∴ 当 AP 的长度为 4 或 9 时,
△ADP 和 △ABC 相似.
1. 如图,已知 △ABC中,D 为边 AC 上一点,P 为边
AB上一点,AB = 12,AC = 8,AD = 6,当 AP 的长
度为 时,△ADP 和 △ABC 相似.
A
B
C
D
4 或 9
P
P
提高训练
2.△ABC为锐角三角形,BD、CE为高 .
求证:△ ADE∽ △ ABC.
A
B
D
C
E
O
证明:∵BD⊥AC,CE⊥AB,
∴∠ABD+∠A=90°,
∠ACE+∠A= 90°.
∴ ∠ABD= ∠ACE.
又∵ ∠A= ∠A,
∴△ ABD ∽ △ ACE.
∴
∵ ∠A= ∠A,
∴ △ ADE ∽ △ ABC.
DE‖AB
∠B=∠AED
AB‖CD
∠A=∠C
∠BAC=900
AD⊥BC
∠BAD=∠C
本节归纳
作业布置:
习题4.6 1,2,3,4
选讲内容:
Rt△ABC中,AD⊥BC,
①AD2=BD.DC
②AB2=BD.BC
③AC2=DC.BC
射影定理
1.如图,直线EF分别交△ABC的边AC,AB于点E,F,交边BC的延长线于点D,且AB?BF= BC?BD.求证: AE?EC= EF?ED.
证明:∵AB·BFBC·=BD,
又∵∠B=∠B,
∴△ABC∽△DBF
又∵∠AEF=∠DEC,
即AE?EC= EF?ED.
∴∠A=∠D.
∴ .△AEF ∽△DEC
2.如图,在矩形ABCD中,AB=1,BC=2,点E在AD上,且ED=3AE.求证:△ABC∽△EAB.
3. 如图,在四边形 ABCD 中,已知 ∠B =∠ACD,
AB=6,BC=4,AC=5,CD= ,求 AD 的长.
A
B
C
D
解:∵AB=6,BC=4,AC=5,CD= ,
∴
又∵∠B=∠ACD,
∴ △ABC ∽ △DCA,
∴ ,
∴
4. 如图,∠DAB =∠CAE,且 AB · AD = AE·AC,求证
△ABC ∽△AED.
A
B
C
D
E
证明:∵ AB · AD = AE·AC,
∴
又∵ ∠DAB =∠CAE,
∴∠ DAB +∠BAE =∠CAE +∠BAE ,
即∠DAE =∠BAC,
∴ △ABC ∽△AED.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
