第3章 实验:探究弹簧弹力的大小与伸长量的关系Word版含解析
文档属性
| 名称 | 第3章 实验:探究弹簧弹力的大小与伸长量的关系Word版含解析 |
|
|
| 格式 | doc | ||
| 文件大小 | 714.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-19 00:00:00 | ||
图片预览




文档简介
实验:探究弹簧弹力的大小与伸长量的关系
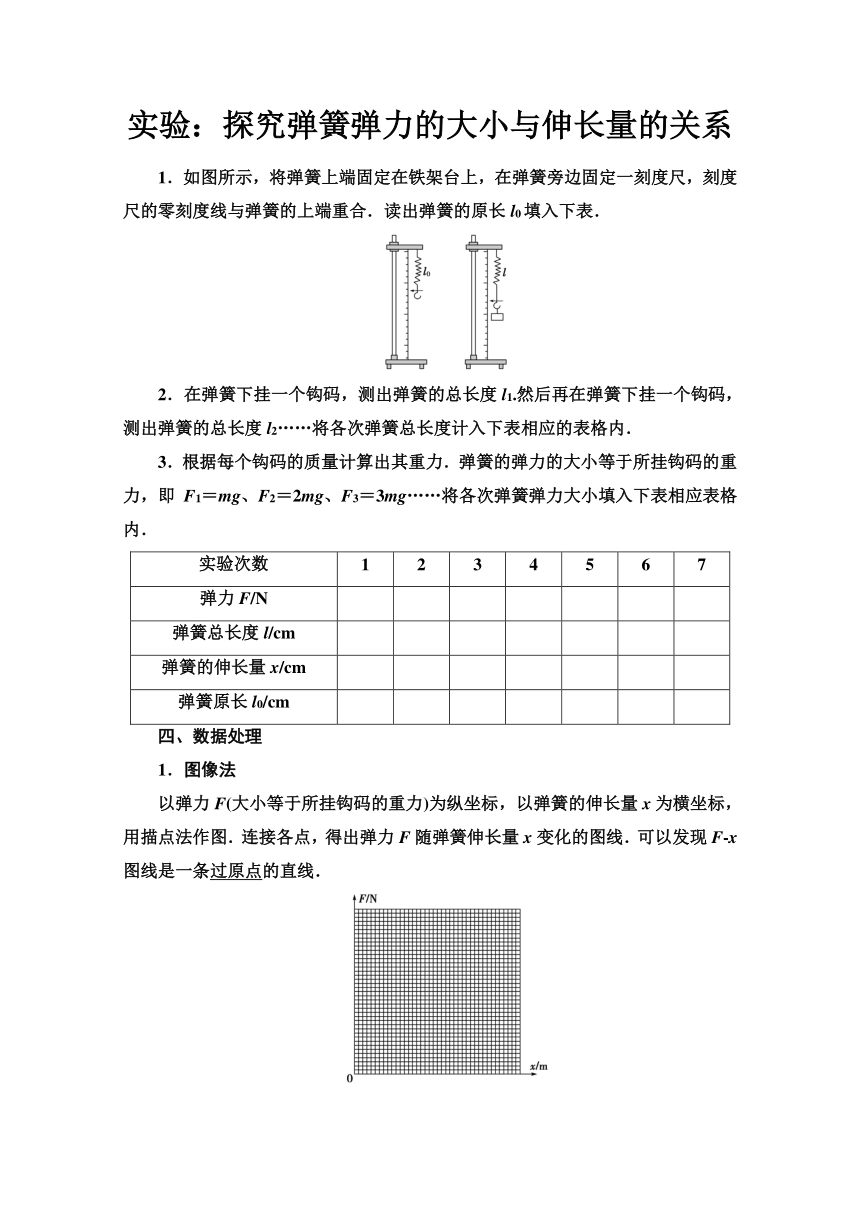
1.如图所示,将弹簧上端固定在铁架台上,在弹簧旁边固定一刻度尺,刻度尺的零刻度线与弹簧的上端重合.读出弹簧的原长l0填入下表.
2.在弹簧下挂一个钩码,测出弹簧的总长度l1.然后再在弹簧下挂一个钩码,测出弹簧的总长度l2……将各次弹簧总长度计入下表相应的表格内.
3.根据每个钩码的质量计算出其重力.弹簧的弹力的大小等于所挂钩码的重力,即F1=mg、F2=2mg、F3=3mg……将各次弹簧弹力大小填入下表相应表格内.
实验次数 1 2 3 4 5 6 7
弹力F/N
弹簧总长度l/cm
弹簧的伸长量x/cm
弹簧原长l0/cm
四、数据处理
1.图像法
以弹力F(大小等于所挂钩码的重力)为纵坐标,以弹簧的伸长量x为横坐标,用描点法作图.连接各点,得出弹力F随弹簧伸长量x变化的图线.可以发现F?x图线是一条过原点的直线.
2.函数法
弹力F与弹簧的伸长量x应满足函数F=kx的关系.
五、误差分析
产生原因 减小方法
偶然误差 测弹簧长度的读数不准 钩码静止,眼睛平视
描点画图不准 点描小些,画图时点尽可能在线上,不在线上的点尽可能分布在线的两侧
系统误差 弹簧自重 选轻质弹簧
六、注意事项
1.所挂钩码不要过重,以免弹簧超出它的弹性限度.
2.每次所挂钩码的质量差尽量大一些,从而使坐标上描的点间距尽量大些,这样作出的图线更精确.
3.测弹簧长度时,一定要在弹簧竖直悬挂且处于平衡状态时测量.
4.记录数据时要注意弹力及弹簧伸长量的对应关系及单位.
5.尽量选用轻质弹簧以便能忽略自身重力的影响.
【例1】 如图(a),一弹簧上端固定在支架顶端,下端悬挂一托盘;一标尺由游标和主尺构成,主尺竖直固定在弹簧左边;托盘上方固定有一能与游标刻度线准确对齐的装置,简化为图中的指针.
图(a) 图(b)
现要测量图(a)中弹簧的劲度系数.当托盘内没有砝码时,移动游标,使其零刻度线对准指针,此时标尺读数为1.950 cm;当托盘内放有质量为0.100 kg的砝码时,移动游标,再次使其零刻度线对准指针,标尺示数如图(b)所示,其读数为________ cm.当地的重力加速度大小为9.80 m/s2,此弹簧的劲度系数为________ N/m(保留3位有效数字).
[解析] 实验所用的游标卡尺最小分度为0.05 mm,游标卡尺上游标第15条刻度线与主尺刻度线对齐,根据游标卡尺的读数规则,图(b)所示的游标卡尺读数为3.7 cm+15×0.05 mm=3.7 cm+0.075 cm=3.775 cm.托盘中放有质量为m=0.100 kg的砝码时,弹簧受到的拉力F=mg=0.100×9.8 N=0.980 N,弹簧伸长量为x=3.775 cm-1.950 cm=1.825 cm,根据胡克定律F=kx,解得此弹簧的劲度系数k==53.7 N/m.
[答案] 3.775 53.7
【例2】 某同学在探究弹力与弹簧伸长量的关系时,设计了如图甲所示的实验装置.他先测出不挂钩码时弹簧的自然长度,然后在弹簧下端依次挂1、2、3、4、5个钩码,待静止时,测出弹簧相应的总长度.每只钩码的质量都是10 g.实验数据如下表所示.(弹力始终未超出弹簧的弹性限度,g取10 N/kg)
钩码质量/g 0 10 20 30 40 50
弹簧总长度/cm 5.00 5.50 6.00 6.50 7.00 7.50
弹力大小/N 0 0.1 0.2 0.3 0.4 0.5
甲 乙
(1)试根据这些实验数据,在图乙所示的坐标纸上作出弹簧弹力大小F跟弹簧总长度l之间的函数关系图像.
(2)图像在l轴上的截距的物理意义是________.该弹簧的劲度系数k=________N/m.
[解析] (1)根据实验数据描点、连线,所得F?l图像如图所示.
(2)图像在l轴上的截距表示弹簧原长.由图像可知,弹簧的劲度系数应等于直线的斜率,即k==20 N/m.
[答案] (1)见解析图 (2)表示弹簧原长 20
处理实验数据的方法
处理实验数据的方法有列表法、图像法、函数法,其中用图像法处理实验数据可以减小偶然误差,是物理实验中常用的方法之一.处理问题时注意:①连线时要注意,使尽可能多的点在所连的直线上,不在直线的点要尽可能分布在直线的两侧,且到直线的距离大致相等.②图线的斜率,是纵轴物理量变化量与横轴物理量变化量的比值.③要灵活应用数学知识,即数形结合,理解图线斜率和截距的物理意义.
1.在“探究弹簧的弹力和其伸长量的关系”的实验中,以下说法正确的是( )
A.弹簧被拉伸时,可以超出它的弹性限度
B.用悬挂钩码的方法给弹簧施加拉力,应保证弹簧位于竖直位置且处于平衡状态
C.用直尺测得弹簧的长度即为弹簧的伸长量
D.用几根不同的弹簧,分别测出几组拉力与伸长量,得出拉力与伸长量之比相等
B [本实验中应以所研究的一根弹簧为实验对象,在弹性限度内通过增减钩码的数目,在竖直方向上改变对弹簧的拉力,来探究弹力与弹簧伸长的关系,所以选B.]
2.某同学利用如图(a)装置做“探究弹簧弹力大小与其长度的关系”的实验.
(1)他通过实验得到如图(b)所示的弹力大小F与弹簧长度x的关系图线,由此图线可得该弹簧的原长x0=________ cm,劲度系数k=________N/m.
(2)他又利用本实验原理把该弹簧做成一把弹簧秤,当弹簧秤上的示数如图(c)所示时,该弹簧的长度x=__________ cm.
[解析] (1)从题图(b)中可以看出,当外力为零时,弹簧的长度为4 cm,即弹簧的原长为4 cm,从图中可得当F=2 N时,弹簧的长度为8 cm,即Δx=4 cm,所以劲度系数为k== N/m=50 N/m.
(2)从题图(c)中可得弹簧的弹力为3.0 N,所以从题图(b)中可以找出,当F=3 N时,弹簧的长度为10 cm.
[答案] (1)4 50 (2)10
3.图甲为某同学用力传感器去探究弹簧的弹力和伸长量的关系的实验情景.用力传感器竖直向下拉上端固定于铁架台的轻质弹簧,读出不同拉力下的标尺刻度x及拉力大小F(从电脑中直接读出).所得数据记录在表格中:
拉力大小F/N 0.45 0.69 0.93 1.14 1.44 1.69
标尺刻度x/cm 57.02 58.01 59.00 60.00 61.03 62.00
(1)从图乙读出刻度尺上的刻度值为________cm.
(2)根据所测数据,在图丙坐标纸上作出F与x的关系图像.
(3)由图像求出该弹簧的劲度系数为________N/m,弹簧的原长为________cm.(均保留三位有效数字)
[解析] (1)由图可知,弹簧测力计的最小分度值为0.1 N,故读数为63.60 N.
(2)根据表中数据利用描点法得出对应的图像如图所示.
(3)由胡克定律可知,图像的斜率表示劲度系数,则可知k= N/m=24.1 N/m.图像与横轴的交点为弹簧原长.
[答案] (1)63.60(63.55~63.65都正确)
(2)图见解析
(3)24.1(24.0~25.0都正确) 55.2(55.0~55.5都正确)
4.某同学用如图所示装置做探究弹簧弹力和伸长关系的实验.他先测出不挂钩码时弹簧下端指针所指的标尺刻度,然后在弹簧下端挂上1个钩码,并逐渐增加钩码的个数,测出指针所指的标尺刻度,所得数据列表如下:(重力加速度取g=9.8 N/kg)
砝码质量 m/(×102 g) 0 1.00 2.00 3.00 4.00 5.00 6.00 7.00
标尺刻度x/ (×10-2 m) 15.00 18.94 22.82 26.78 30.66 34.60 42.00 54.50
(1)根据所测数据,在如图所示的坐标纸上作出弹簧指针所指的标尺刻度x与钩码质量m的关系曲线.
(2)根据所测得的数据和关系曲线可以判断,在______N范围内弹力大小与弹簧伸长关系满足胡克定律,这种规格的弹簧的劲度系数为________N/m.
[解析] (1)根据题目中所测量的数据进行描点,然后用平滑的曲线(或直线)连接各点,在连接时应让尽量多的点落在线上.(偏差比较大的点舍去)不在线上的点尽量平均分布在线的两侧,如图.
(2)根据所画图像可以看出,当m≤5.00×102 g=0.5 kg时,标尺刻度x与钩码质量m成一次函数关系,所以当F≤4.9 N时弹力大小与弹簧伸长关系满足胡克定律,由ΔF=kΔx,可得k===25 N/m.
[答案] (1)见解析 (2)4.9 25
5.某研究性学习小组采用实验法探究弹簧的弹力与其伸长量的关系.他们的实验装置如图所示.
(1)多次实验得到下列表格中的数据,分析此表中的数据,说明与弹簧弹力的大小有关的因素为________.
所挂钩码的重力/N 0 0.1 0.2 0.3 0.4 0.5
弹簧长度/cm 甲(粗、短) 10.0 10.5 11.0 11.5 12.0 12.5
乙(细、长) 20.0 22.0 24.0 26.0 28.0 30.0
(2)用图像法分析,建立直角坐标系,以力F为纵坐标,以弹簧的伸长量x为横坐标(如图所示).根据所测的数据在坐标纸上描点,并尝试着作出一条平滑的图线.
(3)通过分析弹簧的弹力F与其伸长量x的关系图像,能得到________________________________________________________________________________________________________________________________________________.(要求用语言和公式两种形式表述)
(4)若将弹簧的弹力大小与对应的形变量之比定义为弹簧的劲度系数k,则甲、乙弹簧的劲度系数分别是______和________.你认为与弹簧的劲度系数有关的因素为_________________________.
[解析] (1)弹簧弹力的大小跟弹簧的伸长量和弹簧本身的性质(如弹簧的粗细、长短等)有关系.
(2)如图所示:
(3)通过分析图像可知,图线为两条过原点的直线,说明弹簧的弹力跟它的伸长量成正比,即F=kx.
(4)由(3)知,图线的斜率为弹簧的劲度系数,由图可知
k甲= N/m=20 N/m
k乙= N/m=5 N/m
劲度系数的大小只与弹簧本身的因素如弹簧的材料、硬度、粗细、长短等有关,而与形变量无关.
[答案] 见解析
6.现有一种纳米合金丝,欲测定出其伸长量x与所受拉力F、长度L的关系.
(1)测量上述物理量需要的主要器材是______、______等.
(2)若实验中测量的数据如表所示,根据这些数据请写出x与F、L间的关系式:x=________.(若用到比例系数,可用k表示,假设实验中合金丝直径的变化可忽略)
长度L/cm 伸长量x/cm 拉力F/N
5.00 0.20 50.0
5.00 0.40 100.0
10.00 0.40 50.0
(3)在研究并得到上述关系的过程中,主要运用的科学研究方法是________(只需写出一种).
(4)若有一根由上述材料制成的粗细相同的合金丝的长度为20 cm,使用中要求其伸长量不能超过原长的百分之一,那么这根合金丝能承受的最大拉力为________ N.
[解析] (1)用弹簧测力计测量力的大小,用刻度尺测量弹簧长度.
(2)由题目所给的数据分析可知:当力一定时,伸长量与长度成正比;当长度一定时,伸长量和力成正比,故x=kFL(取一组数据验证,式中的k不为零).
(3)研究伸长量与拉力、长度的关系时,可以先控制某一个量不变,如长度不变,再研究伸长量与拉力的关系,这种方法称为控制变量法.这是物理实验中的一个重要研究方法.
(4)代入表中数据把式中的k求出,得k=8×10-4N-1,再代入已知数据,L=20 cm,x==0.2 cm,可求得最大拉力F=12.5 N.
[答案] (1)弹簧测力计 刻度尺
(2)kFL (3)控制变量法 (4)12.5
1.如图所示,将弹簧上端固定在铁架台上,在弹簧旁边固定一刻度尺,刻度尺的零刻度线与弹簧的上端重合.读出弹簧的原长l0填入下表.
2.在弹簧下挂一个钩码,测出弹簧的总长度l1.然后再在弹簧下挂一个钩码,测出弹簧的总长度l2……将各次弹簧总长度计入下表相应的表格内.
3.根据每个钩码的质量计算出其重力.弹簧的弹力的大小等于所挂钩码的重力,即F1=mg、F2=2mg、F3=3mg……将各次弹簧弹力大小填入下表相应表格内.
实验次数 1 2 3 4 5 6 7
弹力F/N
弹簧总长度l/cm
弹簧的伸长量x/cm
弹簧原长l0/cm
四、数据处理
1.图像法
以弹力F(大小等于所挂钩码的重力)为纵坐标,以弹簧的伸长量x为横坐标,用描点法作图.连接各点,得出弹力F随弹簧伸长量x变化的图线.可以发现F?x图线是一条过原点的直线.
2.函数法
弹力F与弹簧的伸长量x应满足函数F=kx的关系.
五、误差分析
产生原因 减小方法
偶然误差 测弹簧长度的读数不准 钩码静止,眼睛平视
描点画图不准 点描小些,画图时点尽可能在线上,不在线上的点尽可能分布在线的两侧
系统误差 弹簧自重 选轻质弹簧
六、注意事项
1.所挂钩码不要过重,以免弹簧超出它的弹性限度.
2.每次所挂钩码的质量差尽量大一些,从而使坐标上描的点间距尽量大些,这样作出的图线更精确.
3.测弹簧长度时,一定要在弹簧竖直悬挂且处于平衡状态时测量.
4.记录数据时要注意弹力及弹簧伸长量的对应关系及单位.
5.尽量选用轻质弹簧以便能忽略自身重力的影响.
【例1】 如图(a),一弹簧上端固定在支架顶端,下端悬挂一托盘;一标尺由游标和主尺构成,主尺竖直固定在弹簧左边;托盘上方固定有一能与游标刻度线准确对齐的装置,简化为图中的指针.
图(a) 图(b)
现要测量图(a)中弹簧的劲度系数.当托盘内没有砝码时,移动游标,使其零刻度线对准指针,此时标尺读数为1.950 cm;当托盘内放有质量为0.100 kg的砝码时,移动游标,再次使其零刻度线对准指针,标尺示数如图(b)所示,其读数为________ cm.当地的重力加速度大小为9.80 m/s2,此弹簧的劲度系数为________ N/m(保留3位有效数字).
[解析] 实验所用的游标卡尺最小分度为0.05 mm,游标卡尺上游标第15条刻度线与主尺刻度线对齐,根据游标卡尺的读数规则,图(b)所示的游标卡尺读数为3.7 cm+15×0.05 mm=3.7 cm+0.075 cm=3.775 cm.托盘中放有质量为m=0.100 kg的砝码时,弹簧受到的拉力F=mg=0.100×9.8 N=0.980 N,弹簧伸长量为x=3.775 cm-1.950 cm=1.825 cm,根据胡克定律F=kx,解得此弹簧的劲度系数k==53.7 N/m.
[答案] 3.775 53.7
【例2】 某同学在探究弹力与弹簧伸长量的关系时,设计了如图甲所示的实验装置.他先测出不挂钩码时弹簧的自然长度,然后在弹簧下端依次挂1、2、3、4、5个钩码,待静止时,测出弹簧相应的总长度.每只钩码的质量都是10 g.实验数据如下表所示.(弹力始终未超出弹簧的弹性限度,g取10 N/kg)
钩码质量/g 0 10 20 30 40 50
弹簧总长度/cm 5.00 5.50 6.00 6.50 7.00 7.50
弹力大小/N 0 0.1 0.2 0.3 0.4 0.5
甲 乙
(1)试根据这些实验数据,在图乙所示的坐标纸上作出弹簧弹力大小F跟弹簧总长度l之间的函数关系图像.
(2)图像在l轴上的截距的物理意义是________.该弹簧的劲度系数k=________N/m.
[解析] (1)根据实验数据描点、连线,所得F?l图像如图所示.
(2)图像在l轴上的截距表示弹簧原长.由图像可知,弹簧的劲度系数应等于直线的斜率,即k==20 N/m.
[答案] (1)见解析图 (2)表示弹簧原长 20
处理实验数据的方法
处理实验数据的方法有列表法、图像法、函数法,其中用图像法处理实验数据可以减小偶然误差,是物理实验中常用的方法之一.处理问题时注意:①连线时要注意,使尽可能多的点在所连的直线上,不在直线的点要尽可能分布在直线的两侧,且到直线的距离大致相等.②图线的斜率,是纵轴物理量变化量与横轴物理量变化量的比值.③要灵活应用数学知识,即数形结合,理解图线斜率和截距的物理意义.
1.在“探究弹簧的弹力和其伸长量的关系”的实验中,以下说法正确的是( )
A.弹簧被拉伸时,可以超出它的弹性限度
B.用悬挂钩码的方法给弹簧施加拉力,应保证弹簧位于竖直位置且处于平衡状态
C.用直尺测得弹簧的长度即为弹簧的伸长量
D.用几根不同的弹簧,分别测出几组拉力与伸长量,得出拉力与伸长量之比相等
B [本实验中应以所研究的一根弹簧为实验对象,在弹性限度内通过增减钩码的数目,在竖直方向上改变对弹簧的拉力,来探究弹力与弹簧伸长的关系,所以选B.]
2.某同学利用如图(a)装置做“探究弹簧弹力大小与其长度的关系”的实验.
(1)他通过实验得到如图(b)所示的弹力大小F与弹簧长度x的关系图线,由此图线可得该弹簧的原长x0=________ cm,劲度系数k=________N/m.
(2)他又利用本实验原理把该弹簧做成一把弹簧秤,当弹簧秤上的示数如图(c)所示时,该弹簧的长度x=__________ cm.
[解析] (1)从题图(b)中可以看出,当外力为零时,弹簧的长度为4 cm,即弹簧的原长为4 cm,从图中可得当F=2 N时,弹簧的长度为8 cm,即Δx=4 cm,所以劲度系数为k== N/m=50 N/m.
(2)从题图(c)中可得弹簧的弹力为3.0 N,所以从题图(b)中可以找出,当F=3 N时,弹簧的长度为10 cm.
[答案] (1)4 50 (2)10
3.图甲为某同学用力传感器去探究弹簧的弹力和伸长量的关系的实验情景.用力传感器竖直向下拉上端固定于铁架台的轻质弹簧,读出不同拉力下的标尺刻度x及拉力大小F(从电脑中直接读出).所得数据记录在表格中:
拉力大小F/N 0.45 0.69 0.93 1.14 1.44 1.69
标尺刻度x/cm 57.02 58.01 59.00 60.00 61.03 62.00
(1)从图乙读出刻度尺上的刻度值为________cm.
(2)根据所测数据,在图丙坐标纸上作出F与x的关系图像.
(3)由图像求出该弹簧的劲度系数为________N/m,弹簧的原长为________cm.(均保留三位有效数字)
[解析] (1)由图可知,弹簧测力计的最小分度值为0.1 N,故读数为63.60 N.
(2)根据表中数据利用描点法得出对应的图像如图所示.
(3)由胡克定律可知,图像的斜率表示劲度系数,则可知k= N/m=24.1 N/m.图像与横轴的交点为弹簧原长.
[答案] (1)63.60(63.55~63.65都正确)
(2)图见解析
(3)24.1(24.0~25.0都正确) 55.2(55.0~55.5都正确)
4.某同学用如图所示装置做探究弹簧弹力和伸长关系的实验.他先测出不挂钩码时弹簧下端指针所指的标尺刻度,然后在弹簧下端挂上1个钩码,并逐渐增加钩码的个数,测出指针所指的标尺刻度,所得数据列表如下:(重力加速度取g=9.8 N/kg)
砝码质量 m/(×102 g) 0 1.00 2.00 3.00 4.00 5.00 6.00 7.00
标尺刻度x/ (×10-2 m) 15.00 18.94 22.82 26.78 30.66 34.60 42.00 54.50
(1)根据所测数据,在如图所示的坐标纸上作出弹簧指针所指的标尺刻度x与钩码质量m的关系曲线.
(2)根据所测得的数据和关系曲线可以判断,在______N范围内弹力大小与弹簧伸长关系满足胡克定律,这种规格的弹簧的劲度系数为________N/m.
[解析] (1)根据题目中所测量的数据进行描点,然后用平滑的曲线(或直线)连接各点,在连接时应让尽量多的点落在线上.(偏差比较大的点舍去)不在线上的点尽量平均分布在线的两侧,如图.
(2)根据所画图像可以看出,当m≤5.00×102 g=0.5 kg时,标尺刻度x与钩码质量m成一次函数关系,所以当F≤4.9 N时弹力大小与弹簧伸长关系满足胡克定律,由ΔF=kΔx,可得k===25 N/m.
[答案] (1)见解析 (2)4.9 25
5.某研究性学习小组采用实验法探究弹簧的弹力与其伸长量的关系.他们的实验装置如图所示.
(1)多次实验得到下列表格中的数据,分析此表中的数据,说明与弹簧弹力的大小有关的因素为________.
所挂钩码的重力/N 0 0.1 0.2 0.3 0.4 0.5
弹簧长度/cm 甲(粗、短) 10.0 10.5 11.0 11.5 12.0 12.5
乙(细、长) 20.0 22.0 24.0 26.0 28.0 30.0
(2)用图像法分析,建立直角坐标系,以力F为纵坐标,以弹簧的伸长量x为横坐标(如图所示).根据所测的数据在坐标纸上描点,并尝试着作出一条平滑的图线.
(3)通过分析弹簧的弹力F与其伸长量x的关系图像,能得到________________________________________________________________________________________________________________________________________________.(要求用语言和公式两种形式表述)
(4)若将弹簧的弹力大小与对应的形变量之比定义为弹簧的劲度系数k,则甲、乙弹簧的劲度系数分别是______和________.你认为与弹簧的劲度系数有关的因素为_________________________.
[解析] (1)弹簧弹力的大小跟弹簧的伸长量和弹簧本身的性质(如弹簧的粗细、长短等)有关系.
(2)如图所示:
(3)通过分析图像可知,图线为两条过原点的直线,说明弹簧的弹力跟它的伸长量成正比,即F=kx.
(4)由(3)知,图线的斜率为弹簧的劲度系数,由图可知
k甲= N/m=20 N/m
k乙= N/m=5 N/m
劲度系数的大小只与弹簧本身的因素如弹簧的材料、硬度、粗细、长短等有关,而与形变量无关.
[答案] 见解析
6.现有一种纳米合金丝,欲测定出其伸长量x与所受拉力F、长度L的关系.
(1)测量上述物理量需要的主要器材是______、______等.
(2)若实验中测量的数据如表所示,根据这些数据请写出x与F、L间的关系式:x=________.(若用到比例系数,可用k表示,假设实验中合金丝直径的变化可忽略)
长度L/cm 伸长量x/cm 拉力F/N
5.00 0.20 50.0
5.00 0.40 100.0
10.00 0.40 50.0
(3)在研究并得到上述关系的过程中,主要运用的科学研究方法是________(只需写出一种).
(4)若有一根由上述材料制成的粗细相同的合金丝的长度为20 cm,使用中要求其伸长量不能超过原长的百分之一,那么这根合金丝能承受的最大拉力为________ N.
[解析] (1)用弹簧测力计测量力的大小,用刻度尺测量弹簧长度.
(2)由题目所给的数据分析可知:当力一定时,伸长量与长度成正比;当长度一定时,伸长量和力成正比,故x=kFL(取一组数据验证,式中的k不为零).
(3)研究伸长量与拉力、长度的关系时,可以先控制某一个量不变,如长度不变,再研究伸长量与拉力的关系,这种方法称为控制变量法.这是物理实验中的一个重要研究方法.
(4)代入表中数据把式中的k求出,得k=8×10-4N-1,再代入已知数据,L=20 cm,x==0.2 cm,可求得最大拉力F=12.5 N.
[答案] (1)弹簧测力计 刻度尺
(2)kFL (3)控制变量法 (4)12.5
同课章节目录
- 绪论 撩开物理学的神秘面纱
- 一、源自然之问
- 二、探万物之秘
- 三、采科学之益
- 四、启智慧之迪
- 第1章 运动的描述
- 第1节 空间和时间
- 第2节 质点和位移
- 第3节 速度
- 第4节 加速度
- 第2章 匀变速直线运动
- 第1节 速度变化规律
- 第2节 位移变化规律
- 第3节 实验中的误差和有效数字
- 第4节 科学测量:做直线运动物体的瞬时速度
- 第5节 自由落体运动
- 第3章 相互作用
- 第1节 重力与重心
- 第2节 科学探究:弹力
- 第3节 摩擦力
- 第4章 力与平衡
- 第1节 科学探究:力的合成
- 第2节 力的分解
- 第3节 共点力的平衡
- 第5章 牛顿运动定律
- 第1节 牛顿第一运动定律
- 第2节 科学探究:加速度与力、质量的关系
- 第3节 牛顿第二运动定律
- 第4节 牛顿第三运动定律
- 第5节 超重与失重
