2020-2021学年度苏科版八年级上册数学3.1勾股定理(2)培优训练卷(Word版 含部分答案)
文档属性
| 名称 | 2020-2021学年度苏科版八年级上册数学3.1勾股定理(2)培优训练卷(Word版 含部分答案) | 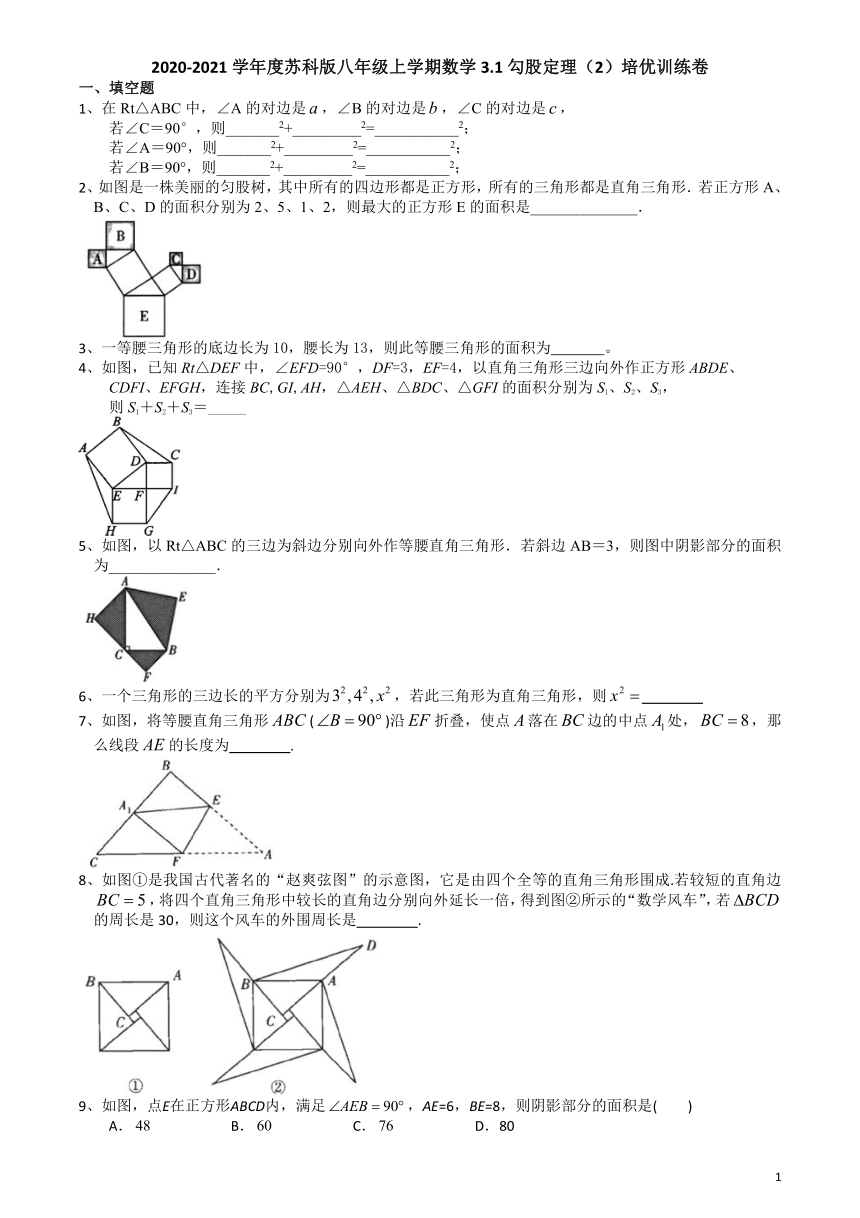 | |
| 格式 | zip | ||
| 文件大小 | 952.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-19 15:31:47 | ||
图片预览



文档简介
2020-2021学年度苏科版八年级上学期数学3.1勾股定理(2)培优训练卷
一、填空题
1、在Rt△ABC中,∠A的对边是,∠B的对边是,∠C的对边是,
若∠C=90°,则_______2+_________2=___________2;
若∠A=90°,则_______2+_________2=___________2;
若∠B=90°,则_______2+_________2=___________2;
2、如图是一株美丽的匀股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、
B、C、D的面积分别为2、5、1、2,则最大的正方形E的面积是______________.
3、一等腰三角形的底边长为10,腰长为13,则此等腰三角形的面积为
。
4、如图,已知Rt△DEF中,∠EFD=90°,DF=3,EF=4,以直角三角形三边向外作正方形ABDE、
CDFI、EFGH,连接BC,GI,AH,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,
则S1+S2+S3=_____
5、如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为______________.
6、一个三角形的三边长的平方分别为,若此三角形为直角三角形,则
7、如图,将等腰直角三角形()沿折叠,使点落在边的中点处,,那么线段的长度为
.
8、如图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成.若较短的直角边,将四个直角三角形中较长的直角边分别向外延长一倍,得到图②所示的“数学风车”,若的周长是30,则这个风车的外围周长是
.
9、如图,点E在正方形ABCD内,满足,AE=6,BE=8,则阴影部分的面积是(
)
A.
B.
C.
D.80
10、如图,把矩形纸片
ABCD
沿
EF
折叠,使点
B
落在边
AD
上的点
B′处,点
A
落在点
A′处,已知
AE=3,BF=5,则
B′E=______,AB=
_______.
二、选择题
11、下列各数组中,不能作为直角三角形三边长的是
(
)
A.
9,12,15
B.
7,24,25
C.
6,8,10
D.
3,5,7
12、若直角三角形的三边为6、8、x,则x的长为
(
)
A.6
B.8
C.10
D.以上答案均不对
13、“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长的直角边长为,较短的直角边长为.若,大正方形的面积为25,则小正方形的边长为(
)
A.
9
B.
6
C.
4
D.
3
14、在直线上依次摆放着三个正方形(如图所示).
已知斜放的正方形的面积是,正放置的两个正方形的面积依次是,则之间的关系是(
)
A.
B.
C.
D.无法确定
15、如图,美国第20任总统加菲尔德利用该图验证了勾股定理,
则在验证过程中用到的面积相等的关系是(
)
A.
B.
C.
D.
16、勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图(a)是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图(b)是由图(a)放人长方形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为
(
)
A.90
B.100
C.110
D.121
17、如图,带阴影的长方形的面积是(
)
A.
9
cm2
B.
24
cm2
C.
45
cm2
D.
51
cm2
18、如图,将边长为6的正方形纸片ABCD折叠,使点D落在AB边中点E处,点C落在点Q处,折痕为FH,则线段AF的长为
(
)
A.2
B.
C.
D.4
三、解答题
19、如图,在⊿ABC中,∠ACB=900,AB=10cm,BC=6cm,CD⊥AB与D,求
CD的长。
20、如图
,为了求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160米,BC长128米.问从点A穿过湖到点B有多远?
?
?
21、如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
(Ⅰ)计算AC+BC的值等于_______ ;
(Ⅱ)请在如图所示的网格中,用无刻度的直尺,画出一个以AB为一边的矩形,使该矩形的面积等于AC+BC,并简要说明画图方法(不要求证明)
22、和是两直角边为,斜边为的全等的直角三角形,按如图所示摆放,其中,求证:
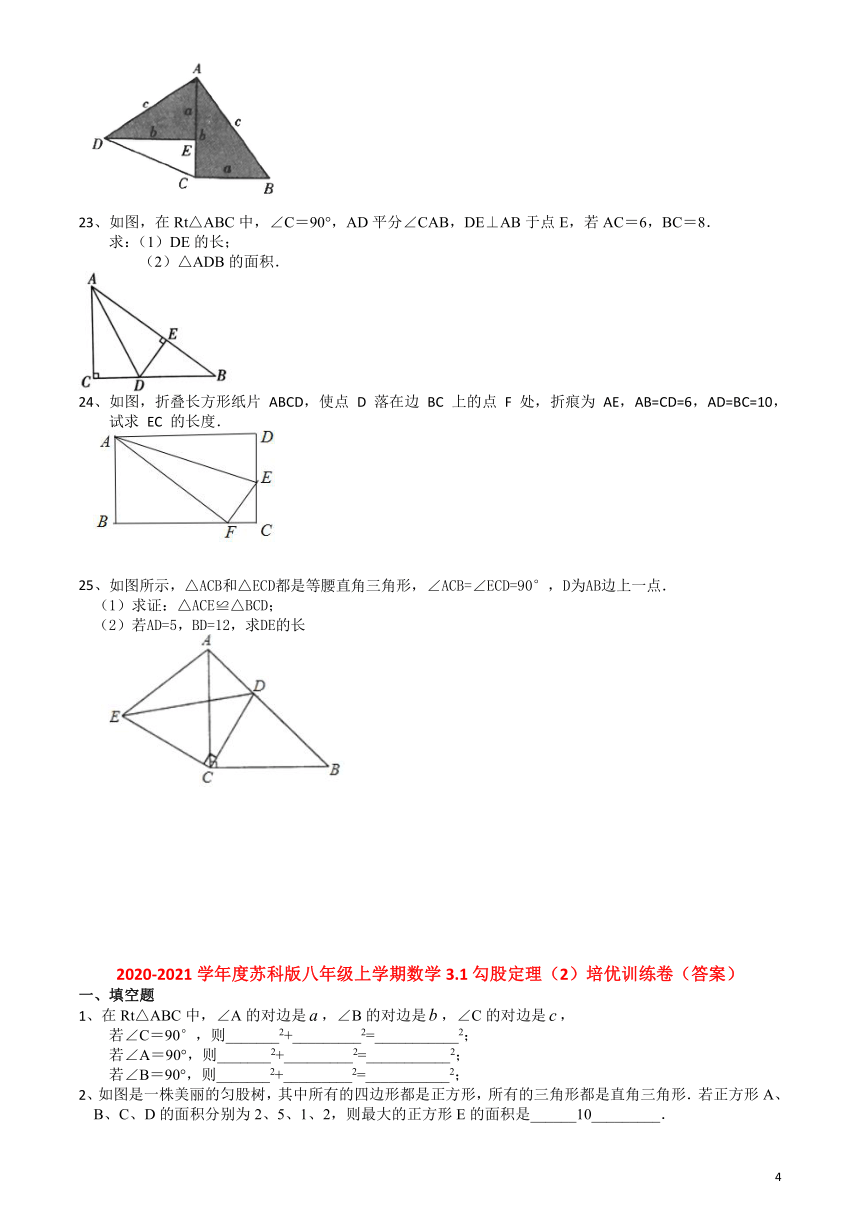
23、如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AC=6,BC=8.
求:(1)DE的长;
(2)△ADB的面积.
24、如图,折叠长方形纸片
ABCD,使点
D
落在边
BC
上的点
F
处,折痕为
AE,AB=CD=6,AD=BC=10,
试求
EC
的长度.
25、如图所示,△ACB
和△ECD
都是等腰直角三角形,∠ACB=∠ECD=90°,D
为
AB
边上一点.
(1)求证:△ACE≌△BCD;
(2)若
AD=5,BD=12,求
DE
的长
2020-2021学年度苏科版八年级上学期数学3.1勾股定理(2)培优训练卷(答案)
一、填空题
1、在Rt△ABC中,∠A的对边是,∠B的对边是,∠C的对边是,
若∠C=90°,则_______2+_________2=___________2;
若∠A=90°,则_______2+_________2=___________2;
若∠B=90°,则_______2+_________2=___________2;
2、如图是一株美丽的匀股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、
B、C、D的面积分别为2、5、1、2,则最大的正方形E的面积是______10_________.
3、一等腰三角形的底边长为10,腰长为13,则此等腰三角形的面积为
60
。
4、如图,已知Rt△DEF中,∠EFD=90°,DF=3,EF=4,以直角三角形三边向外作正方形ABDE、
CDFI、EFGH,连接BC,GI,AH,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,
则S1+S2+S3=__18___
5、如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为______4.5________.
6、一个三角形的三边长的平方分别为,若此三角形为直角三角形,则
25或7
7、如图,将等腰直角三角形()沿折叠,使点落在边的中点处,,那么线段的长度为
5
.
8、如图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成.若较短的直角边,将四个直角三角形中较长的直角边分别向外延长一倍,得到图②所示的“数学风车”,若的周长是30,则这个风车的外围周长是
.
答案:
设BD=x,
AC=AD=y,则x=4y+5,
x+2y+5=30,
∴x=13,y=6,
∴这个风车的外围周长是4(x+y)=76
9、如图,点E在正方形ABCD内,满足,AE=6,BE=8,则阴影部分的面积是(
C
)
A.
B.
C.
D.80
10、如图,把矩形纸片
ABCD
沿
EF
折叠,使点
B
落在边
AD
上的点
B′处,点
A
落在点
A′处,已知
AE=3,BF=5,则
B′E=______,AB=
_______.
二、选择题
11、下列各数组中,不能作为直角三角形三边长的是
(
D
)
A.
9,12,15
B.
7,24,25
C.
6,8,10
D.
3,5,7
12、若直角三角形的三边为6、8、x,则x的长为
(
D
)
A.6
B.8
C.10
D.以上答案均不对
13、“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长的直角边长为,较短的直角边长为.若,大正方形的面积为25,则小正方形的边长为(
D
)
A.
9
B.
6
C.
4
D.
3
14、在直线上依次摆放着三个正方形(如图所示).
已知斜放的正方形的面积是,正放置的两个正方形的面积依次是,则之间的关系是(
A
)
A.
B.
C.
D.无法确定
15、如图,美国第20任总统加菲尔德利用该图验证了勾股定理,
则在验证过程中用到的面积相等的关系是(
D
)
A.
B.
C.
D.
16、勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图(a)是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图(b)是由图(a)放人长方形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为
(
C
)
A.90
B.100
C.110
D.121
17、如图,带阴影的长方形的面积是(
C
)
A.
9
cm2
B.
24
cm2
C.
45
cm2
D.
51
cm2
18、如图,将边长为6的正方形纸片ABCD折叠,使点D落在AB边中点E处,点C落在点Q处,折痕为FH,则线段AF的长为
(
B
)
A.2
B.
C.
D.4
三、解答题
19、如图,在⊿ABC中,∠ACB=900,AB=10cm,BC=6cm,CD⊥AB与D,求
CD的长。
20、如图
,为了求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160米,BC长128米.问从点A穿过湖到点B有多远?
?
?
21、如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
(Ⅰ)计算AC+BC的值等于_______ ;
(Ⅱ)请在如图所示的网格中,用无刻度的直尺,画出一个以AB为一边的矩形,使该矩形的面积等于AC+BC,并简要说明画图方法(不要求证明)
22、和是两直角边为,斜边为的全等的直角三角形,按如图所示摆放,其中,求证:
23、如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AC=6,BC=8.
求:(1)DE的长;
(2)△ADB的面积.
(答案:3,15)
24、如图,折叠长方形纸片
ABCD,使点
D
落在边
BC
上的点
F
处,折痕为
AE,AB=CD=6,AD=BC=10,
试求
EC
的长度.
(答案:)
25、如图所示,△ACB
和△ECD
都是等腰直角三角形,∠ACB=∠ECD=90°,D
为
AB
边上一点.
(1)求证:△ACE≌△BCD;
(2)若
AD=5,BD=12,求
DE
的长
一、填空题
1、在Rt△ABC中,∠A的对边是,∠B的对边是,∠C的对边是,
若∠C=90°,则_______2+_________2=___________2;
若∠A=90°,则_______2+_________2=___________2;
若∠B=90°,则_______2+_________2=___________2;
2、如图是一株美丽的匀股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、
B、C、D的面积分别为2、5、1、2,则最大的正方形E的面积是______________.
3、一等腰三角形的底边长为10,腰长为13,则此等腰三角形的面积为
。
4、如图,已知Rt△DEF中,∠EFD=90°,DF=3,EF=4,以直角三角形三边向外作正方形ABDE、
CDFI、EFGH,连接BC,GI,AH,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,
则S1+S2+S3=_____
5、如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为______________.
6、一个三角形的三边长的平方分别为,若此三角形为直角三角形,则
7、如图,将等腰直角三角形()沿折叠,使点落在边的中点处,,那么线段的长度为
.
8、如图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成.若较短的直角边,将四个直角三角形中较长的直角边分别向外延长一倍,得到图②所示的“数学风车”,若的周长是30,则这个风车的外围周长是
.
9、如图,点E在正方形ABCD内,满足,AE=6,BE=8,则阴影部分的面积是(
)
A.
B.
C.
D.80
10、如图,把矩形纸片
ABCD
沿
EF
折叠,使点
B
落在边
AD
上的点
B′处,点
A
落在点
A′处,已知
AE=3,BF=5,则
B′E=______,AB=
_______.
二、选择题
11、下列各数组中,不能作为直角三角形三边长的是
(
)
A.
9,12,15
B.
7,24,25
C.
6,8,10
D.
3,5,7
12、若直角三角形的三边为6、8、x,则x的长为
(
)
A.6
B.8
C.10
D.以上答案均不对
13、“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长的直角边长为,较短的直角边长为.若,大正方形的面积为25,则小正方形的边长为(
)
A.
9
B.
6
C.
4
D.
3
14、在直线上依次摆放着三个正方形(如图所示).
已知斜放的正方形的面积是,正放置的两个正方形的面积依次是,则之间的关系是(
)
A.
B.
C.
D.无法确定
15、如图,美国第20任总统加菲尔德利用该图验证了勾股定理,
则在验证过程中用到的面积相等的关系是(
)
A.
B.
C.
D.
16、勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图(a)是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图(b)是由图(a)放人长方形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为
(
)
A.90
B.100
C.110
D.121
17、如图,带阴影的长方形的面积是(
)
A.
9
cm2
B.
24
cm2
C.
45
cm2
D.
51
cm2
18、如图,将边长为6的正方形纸片ABCD折叠,使点D落在AB边中点E处,点C落在点Q处,折痕为FH,则线段AF的长为
(
)
A.2
B.
C.
D.4
三、解答题
19、如图,在⊿ABC中,∠ACB=900,AB=10cm,BC=6cm,CD⊥AB与D,求
CD的长。
20、如图
,为了求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160米,BC长128米.问从点A穿过湖到点B有多远?
?
?
21、如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
(Ⅰ)计算AC+BC的值等于_______ ;
(Ⅱ)请在如图所示的网格中,用无刻度的直尺,画出一个以AB为一边的矩形,使该矩形的面积等于AC+BC,并简要说明画图方法(不要求证明)
22、和是两直角边为,斜边为的全等的直角三角形,按如图所示摆放,其中,求证:
23、如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AC=6,BC=8.
求:(1)DE的长;
(2)△ADB的面积.
24、如图,折叠长方形纸片
ABCD,使点
D
落在边
BC
上的点
F
处,折痕为
AE,AB=CD=6,AD=BC=10,
试求
EC
的长度.
25、如图所示,△ACB
和△ECD
都是等腰直角三角形,∠ACB=∠ECD=90°,D
为
AB
边上一点.
(1)求证:△ACE≌△BCD;
(2)若
AD=5,BD=12,求
DE
的长
2020-2021学年度苏科版八年级上学期数学3.1勾股定理(2)培优训练卷(答案)
一、填空题
1、在Rt△ABC中,∠A的对边是,∠B的对边是,∠C的对边是,
若∠C=90°,则_______2+_________2=___________2;
若∠A=90°,则_______2+_________2=___________2;
若∠B=90°,则_______2+_________2=___________2;
2、如图是一株美丽的匀股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、
B、C、D的面积分别为2、5、1、2,则最大的正方形E的面积是______10_________.
3、一等腰三角形的底边长为10,腰长为13,则此等腰三角形的面积为
60
。
4、如图,已知Rt△DEF中,∠EFD=90°,DF=3,EF=4,以直角三角形三边向外作正方形ABDE、
CDFI、EFGH,连接BC,GI,AH,△AEH、△BDC、△GFI的面积分别为S1、S2、S3,
则S1+S2+S3=__18___
5、如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为______4.5________.
6、一个三角形的三边长的平方分别为,若此三角形为直角三角形,则
25或7
7、如图,将等腰直角三角形()沿折叠,使点落在边的中点处,,那么线段的长度为
5
.
8、如图①是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成.若较短的直角边,将四个直角三角形中较长的直角边分别向外延长一倍,得到图②所示的“数学风车”,若的周长是30,则这个风车的外围周长是
.
答案:
设BD=x,
AC=AD=y,则x=4y+5,
x+2y+5=30,
∴x=13,y=6,
∴这个风车的外围周长是4(x+y)=76
9、如图,点E在正方形ABCD内,满足,AE=6,BE=8,则阴影部分的面积是(
C
)
A.
B.
C.
D.80
10、如图,把矩形纸片
ABCD
沿
EF
折叠,使点
B
落在边
AD
上的点
B′处,点
A
落在点
A′处,已知
AE=3,BF=5,则
B′E=______,AB=
_______.
二、选择题
11、下列各数组中,不能作为直角三角形三边长的是
(
D
)
A.
9,12,15
B.
7,24,25
C.
6,8,10
D.
3,5,7
12、若直角三角形的三边为6、8、x,则x的长为
(
D
)
A.6
B.8
C.10
D.以上答案均不对
13、“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长的直角边长为,较短的直角边长为.若,大正方形的面积为25,则小正方形的边长为(
D
)
A.
9
B.
6
C.
4
D.
3
14、在直线上依次摆放着三个正方形(如图所示).
已知斜放的正方形的面积是,正放置的两个正方形的面积依次是,则之间的关系是(
A
)
A.
B.
C.
D.无法确定
15、如图,美国第20任总统加菲尔德利用该图验证了勾股定理,
则在验证过程中用到的面积相等的关系是(
D
)
A.
B.
C.
D.
16、勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图(a)是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图(b)是由图(a)放人长方形内得到的,∠BAC=90°,AB=3,AC=4,点D,E,F,G,H,I都在长方形KLMJ的边上,则长方形KLMJ的面积为
(
C
)
A.90
B.100
C.110
D.121
17、如图,带阴影的长方形的面积是(
C
)
A.
9
cm2
B.
24
cm2
C.
45
cm2
D.
51
cm2
18、如图,将边长为6的正方形纸片ABCD折叠,使点D落在AB边中点E处,点C落在点Q处,折痕为FH,则线段AF的长为
(
B
)
A.2
B.
C.
D.4
三、解答题
19、如图,在⊿ABC中,∠ACB=900,AB=10cm,BC=6cm,CD⊥AB与D,求
CD的长。
20、如图
,为了求出湖两岸的A、B两点之间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC长160米,BC长128米.问从点A穿过湖到点B有多远?
?
?
21、如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
(Ⅰ)计算AC+BC的值等于_______ ;
(Ⅱ)请在如图所示的网格中,用无刻度的直尺,画出一个以AB为一边的矩形,使该矩形的面积等于AC+BC,并简要说明画图方法(不要求证明)
22、和是两直角边为,斜边为的全等的直角三角形,按如图所示摆放,其中,求证:
23、如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,DE⊥AB于点E,若AC=6,BC=8.
求:(1)DE的长;
(2)△ADB的面积.
(答案:3,15)
24、如图,折叠长方形纸片
ABCD,使点
D
落在边
BC
上的点
F
处,折痕为
AE,AB=CD=6,AD=BC=10,
试求
EC
的长度.
(答案:)
25、如图所示,△ACB
和△ECD
都是等腰直角三角形,∠ACB=∠ECD=90°,D
为
AB
边上一点.
(1)求证:△ACE≌△BCD;
(2)若
AD=5,BD=12,求
DE
的长
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
