2020年华师大版八年级上数学课件 :13.3.1 等腰三角形的性质(19张)
文档属性
| 名称 | 2020年华师大版八年级上数学课件 :13.3.1 等腰三角形的性质(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 320.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-19 15:31:51 | ||
图片预览





文档简介
(共19张PPT)
1
等腰三角形的性质
葫芦岛第六初级中学
等腰三角形的性质
等腰三角形的性质:
等腰三角形的两个底角相等(简写成“等边对等角”).
【证明】
如图,△ABC
中,AB=AC,求证:∠B=∠C
.
A
B
C
分析:由上述操作可以得到启发,即添加等腰三角形的顶角平
分线AD,然后证明△ABD
≌
△ACD.
证明:作顶角∠BAC的平分线AD.
在△ABD与△ACD中,
AB=AC(已知),
∠1=∠2(已证),
AD=AD(公共边),
∴
△ABD
≌
△ACD(S.A.S.),
∴
∠B=∠C.
从这里你还可以得到什么结论?
A
B
C
D
(
(
1
2
【
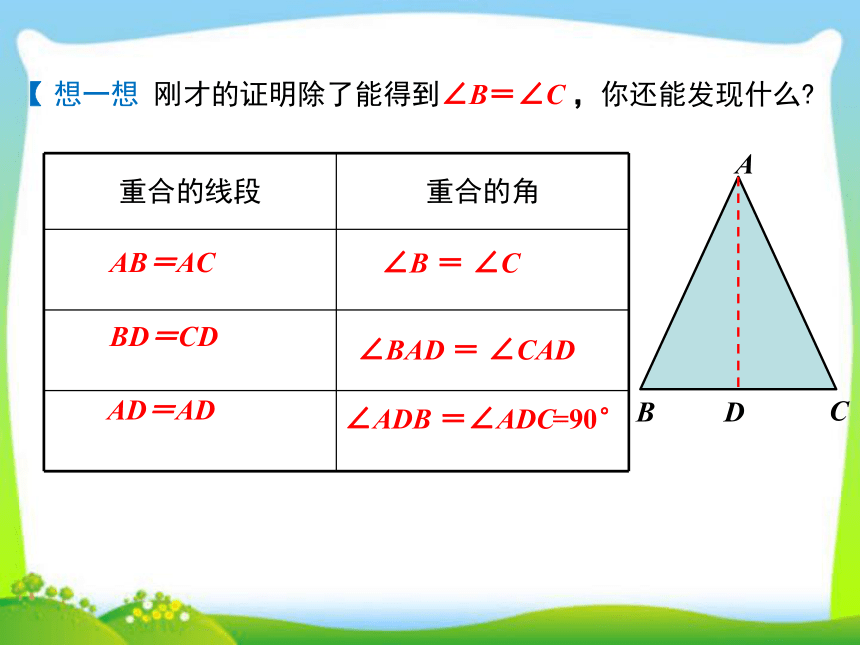
想一想
刚才的证明除了能得到∠B=∠C
,你还能发现什么?
重合的线段
重合的角
A
B
D
C
AB=AC
BD=CD
AD=AD
∠B
=
∠C
∠BAD
=
∠CAD
∠ADB
=∠ADC
=90°
【性质】
等腰三角形底边上的高、中线及顶角的平分线,互相重合(简称“三线合一”).
A
B
C
D
(
(
1
2
【填一填】根据等腰三角形性质完成下列填空.
在△ABC中,
AB=AC时,
(1)∵AD是底边上的高,
∴∠_____
=
∠_____,____=
____.
(2)
∵AD是中线,
∴____⊥____
,∠_____
=∠_____.
(3)
∵AD是角平分线,
∴____
⊥____
,_____
=_____.
1
2
2
BD
CD
AD
BC
BD
1
BC
AD
CD
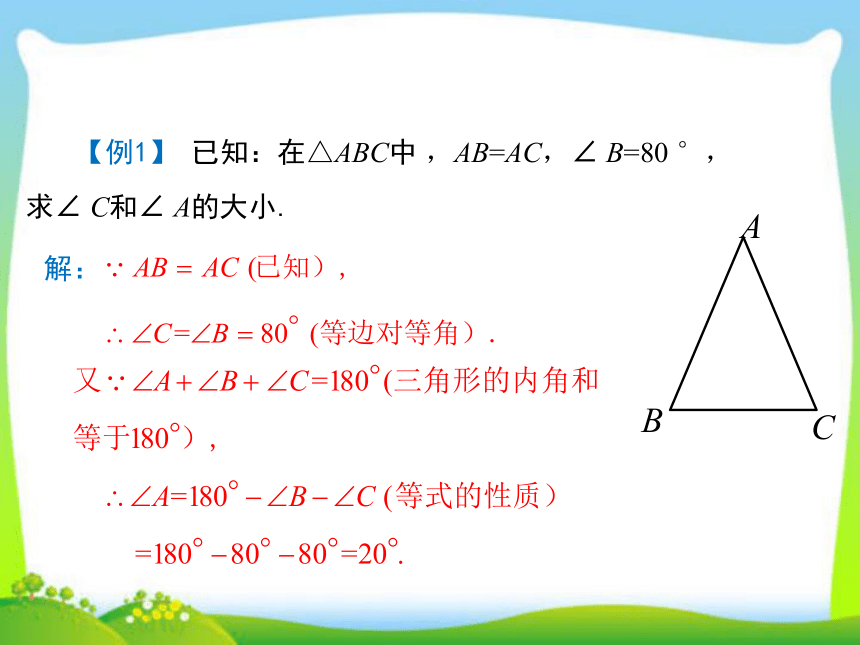
【例1】
已知:在△ABC中
,AB=AC,∠
B=80
°,求∠
C和∠
A的大小.
解:
【例2】
在△ABC中
,AB=AC,D是BC边上的中点,
∠B=30°.求:(1)∠
ADC的大小;(2)∠1的大小.
A
D
C
1
2
(2)∵∠1
+∠B
+∠ADB=180°
(三角形内角和等于180°),
∠B=30°
(已知),
∴∠1=180°-∠B-∠ADB
=180°-30°-90°=60°.
∴AD⊥BC(等腰三角形
“三线合一”).
∴∠ADC
=∠ADB=90°(垂直的定义).
解:(1)
∵AB
=
AC,BD=DC(已知),
B
三条边都相等的三角形是等边三角形,它也是轴对称图形,那么等边三角形的每个角的度数是多少呢?它有几条对称轴?
等边三角形的性质
因为等边三角形是特殊的等腰三角形,由等腰三角形等边对等角的性质得到,∠B=
∠
C,
同理可得
∠A=∠B,
所以
∠A=∠B=∠C,
又由
∠A+∠B+∠C=180°,
从而推出
∠A=∠B=∠C=60°.
也就是说:等边三角形的各个角都相等,并且每一个角都等于60°.
等边三角形的三条边都相等,三个角
都相等,也称为正三角形.
A
C
B
三条对称轴
A
B
C
D
【例3】
如图,在△ABC中
,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
(1)找出图中所有相等的角;
(2)指出图中有几个等腰三角形?
∠A=∠ABD,
∠C=∠BDC=∠ABC.
△ABC,
△ABD,
△BCD.
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
(3)观察∠BDC与∠A、∠ABD的关系,∠ABC、∠C呢?
∠BDC=
∠A+
∠ABD=2
∠A=2
∠ABD,
∠ABC=
∠BDC=2
∠A,
∠C=
∠BDC=2
∠A.
(4)设∠A=x,请把△
ABC的内角和用含x的式子表示出来.
∵
∠A+
∠ABC+
∠
C=180
°,
∴x+2x+2x=180
°.
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,
∠A=∠ABD.
设∠A=x,则∠BDC=
∠A+
∠ABD=2x,
从而∠ABC=
∠C=
∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180
°
,
解得x=36
°
.
在△ABC中,∠A=36°,∠ABC=∠C=72°.
x
⌒
2x
⌒
2x
⌒
⌒
2x
1.
如图,在下列等腰三角形中,分别求出它们的底角的度数.
A
B
C
120°
A
B
C
36°
∠B=∠C
=
72°
∠B=∠C
=
30°
2.(1)等腰三角形一个底角为75°,它的另外两个角为
;
(2)等腰三角形一个角为36°,它的另外两个角为
____________________;
(3)等腰三角形一个角为120°,它的另外两个角为
.
75°,
30°
72°,72°或36°,108°
30°,30°
结论:在等腰三角形中,注意对角的分类讨论.
①
顶角+2×底角=180°
②
顶角=180°-2×底角
③
底角=(180°-顶角)÷2
④0°<顶角<180°
⑤0°<底角<90°
A
C
B
D
3.
如图,是西安半坡博物馆屋顶的截面图,已经知道它的两边AB和AC是相等的.建筑工人师傅对这个建筑物做出了两个判断:
①工人师傅在测量了∠B为37°以后,并没有测量∠C
,就说∠C
的度数也是37°;②工人师傅要加固屋顶,他们通过测量找到了横梁BC的中点D,然后在AD两点之间钉上一根木桩,他们认为木桩是垂直横梁的.
请同学们想想,工人师傅的说法对吗?请说明理由.
工人师傅的说法是对的,△ABC是等腰三角形,根据等腰三角形的性质可以得出这样的结论.
A
C
B
D
请同学们想想,工人师傅的说法对吗?请说明理由.
等腰三角形的性质
等边对等角
等边三角形
注意是指同一个三角形中
注意:顶角的平分线、底边上的高和中线才有这一性质.而腰上高、中线和底角的平分线不具有这一性质
三线合一
有三条对称轴,每个内角等于60°
课堂总结
1
等腰三角形的性质
葫芦岛第六初级中学
等腰三角形的性质
等腰三角形的性质:
等腰三角形的两个底角相等(简写成“等边对等角”).
【证明】
如图,△ABC
中,AB=AC,求证:∠B=∠C
.
A
B
C
分析:由上述操作可以得到启发,即添加等腰三角形的顶角平
分线AD,然后证明△ABD
≌
△ACD.
证明:作顶角∠BAC的平分线AD.
在△ABD与△ACD中,
AB=AC(已知),
∠1=∠2(已证),
AD=AD(公共边),
∴
△ABD
≌
△ACD(S.A.S.),
∴
∠B=∠C.
从这里你还可以得到什么结论?
A
B
C
D
(
(
1
2
【
想一想
刚才的证明除了能得到∠B=∠C
,你还能发现什么?
重合的线段
重合的角
A
B
D
C
AB=AC
BD=CD
AD=AD
∠B
=
∠C
∠BAD
=
∠CAD
∠ADB
=∠ADC
=90°
【性质】
等腰三角形底边上的高、中线及顶角的平分线,互相重合(简称“三线合一”).
A
B
C
D
(
(
1
2
【填一填】根据等腰三角形性质完成下列填空.
在△ABC中,
AB=AC时,
(1)∵AD是底边上的高,
∴∠_____
=
∠_____,____=
____.
(2)
∵AD是中线,
∴____⊥____
,∠_____
=∠_____.
(3)
∵AD是角平分线,
∴____
⊥____
,_____
=_____.
1
2
2
BD
CD
AD
BC
BD
1
BC
AD
CD
【例1】
已知:在△ABC中
,AB=AC,∠
B=80
°,求∠
C和∠
A的大小.
解:
【例2】
在△ABC中
,AB=AC,D是BC边上的中点,
∠B=30°.求:(1)∠
ADC的大小;(2)∠1的大小.
A
D
C
1
2
(2)∵∠1
+∠B
+∠ADB=180°
(三角形内角和等于180°),
∠B=30°
(已知),
∴∠1=180°-∠B-∠ADB
=180°-30°-90°=60°.
∴AD⊥BC(等腰三角形
“三线合一”).
∴∠ADC
=∠ADB=90°(垂直的定义).
解:(1)
∵AB
=
AC,BD=DC(已知),
B
三条边都相等的三角形是等边三角形,它也是轴对称图形,那么等边三角形的每个角的度数是多少呢?它有几条对称轴?
等边三角形的性质
因为等边三角形是特殊的等腰三角形,由等腰三角形等边对等角的性质得到,∠B=
∠
C,
同理可得
∠A=∠B,
所以
∠A=∠B=∠C,
又由
∠A+∠B+∠C=180°,
从而推出
∠A=∠B=∠C=60°.
也就是说:等边三角形的各个角都相等,并且每一个角都等于60°.
等边三角形的三条边都相等,三个角
都相等,也称为正三角形.
A
C
B
三条对称轴
A
B
C
D
【例3】
如图,在△ABC中
,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
(1)找出图中所有相等的角;
(2)指出图中有几个等腰三角形?
∠A=∠ABD,
∠C=∠BDC=∠ABC.
△ABC,
△ABD,
△BCD.
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
(3)观察∠BDC与∠A、∠ABD的关系,∠ABC、∠C呢?
∠BDC=
∠A+
∠ABD=2
∠A=2
∠ABD,
∠ABC=
∠BDC=2
∠A,
∠C=
∠BDC=2
∠A.
(4)设∠A=x,请把△
ABC的内角和用含x的式子表示出来.
∵
∠A+
∠ABC+
∠
C=180
°,
∴x+2x+2x=180
°.
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,
∠A=∠ABD.
设∠A=x,则∠BDC=
∠A+
∠ABD=2x,
从而∠ABC=
∠C=
∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180
°
,
解得x=36
°
.
在△ABC中,∠A=36°,∠ABC=∠C=72°.
x
⌒
2x
⌒
2x
⌒
⌒
2x
1.
如图,在下列等腰三角形中,分别求出它们的底角的度数.
A
B
C
120°
A
B
C
36°
∠B=∠C
=
72°
∠B=∠C
=
30°
2.(1)等腰三角形一个底角为75°,它的另外两个角为
;
(2)等腰三角形一个角为36°,它的另外两个角为
____________________;
(3)等腰三角形一个角为120°,它的另外两个角为
.
75°,
30°
72°,72°或36°,108°
30°,30°
结论:在等腰三角形中,注意对角的分类讨论.
①
顶角+2×底角=180°
②
顶角=180°-2×底角
③
底角=(180°-顶角)÷2
④0°<顶角<180°
⑤0°<底角<90°
A
C
B
D
3.
如图,是西安半坡博物馆屋顶的截面图,已经知道它的两边AB和AC是相等的.建筑工人师傅对这个建筑物做出了两个判断:
①工人师傅在测量了∠B为37°以后,并没有测量∠C
,就说∠C
的度数也是37°;②工人师傅要加固屋顶,他们通过测量找到了横梁BC的中点D,然后在AD两点之间钉上一根木桩,他们认为木桩是垂直横梁的.
请同学们想想,工人师傅的说法对吗?请说明理由.
工人师傅的说法是对的,△ABC是等腰三角形,根据等腰三角形的性质可以得出这样的结论.
A
C
B
D
请同学们想想,工人师傅的说法对吗?请说明理由.
等腰三角形的性质
等边对等角
等边三角形
注意是指同一个三角形中
注意:顶角的平分线、底边上的高和中线才有这一性质.而腰上高、中线和底角的平分线不具有这一性质
三线合一
有三条对称轴,每个内角等于60°
课堂总结
