人教版八年级上册数学 13.2.2 用坐标表示轴对称教案
文档属性
| 名称 | 人教版八年级上册数学 13.2.2 用坐标表示轴对称教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 99.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-20 00:00:00 | ||
图片预览

文档简介
课题
用坐标表示轴对称
课型
新授课
总课时
教学目标
1.在平面直角坐标系中,探索关于x轴、y轴对称的点的坐标规律.
2.利用关于x轴、y轴对称的点的坐标的规律,能作出关于x轴、y轴对称的图形.
3.在用坐标表示轴对称时发展形象思维能力和数形结合的意识.
教学过程
先行独立学习
已知点A(2,-3),B(-1,2),C(-6,-5),D(,1),E(4,0).
关于x轴的对称点A′(____,____)B′(_____,______)C′(_____,_____)D′(____,_____)E′(_____,_____).
关于y轴的对称点A″(_____,____)B″(_____,______)C″(_____,_____)D″(____,_____)E″(_____,_____).
迁移导入
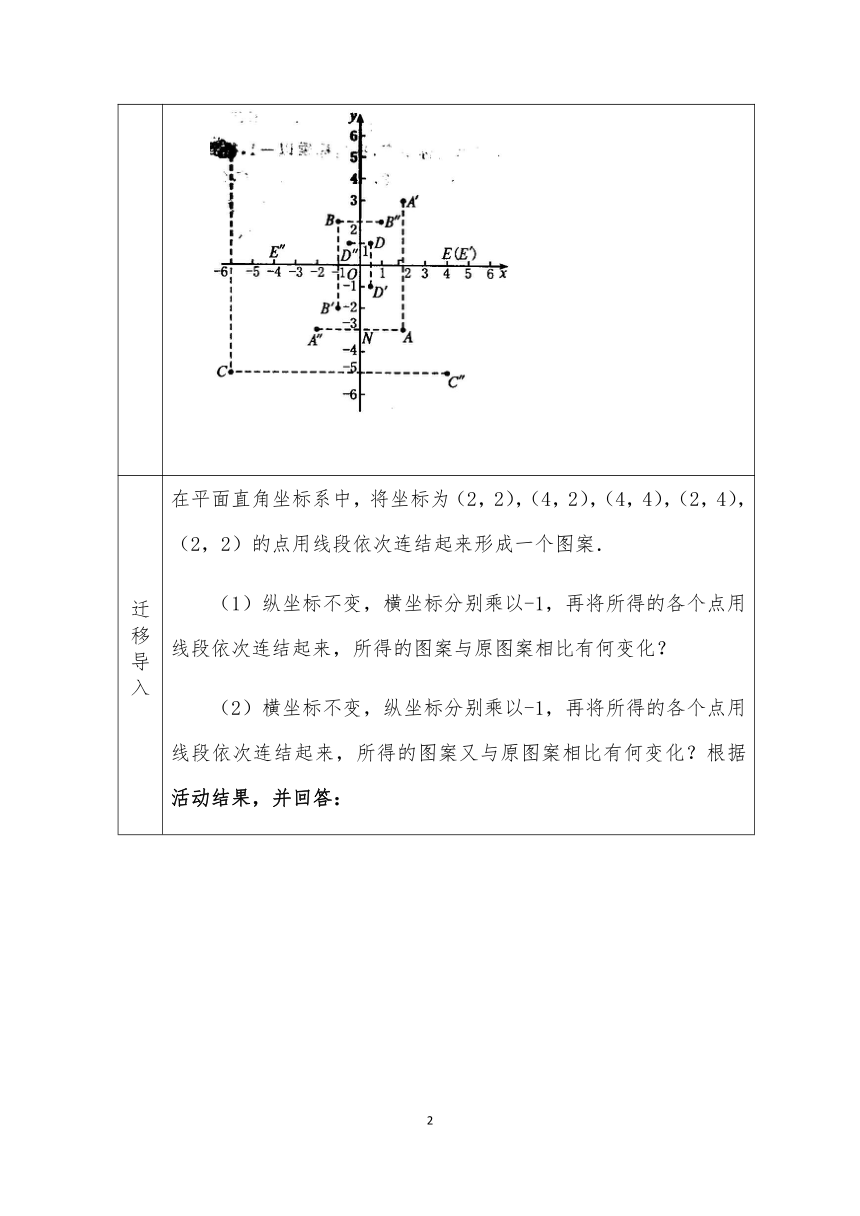
在平面直角坐标系中,将坐标为(2,2),(4,2),(4,4),(2,4),(2,2)的点用线段依次连结起来形成一个图案.
(1)纵坐标不变,横坐标分别乘以-1,再将所得的各个点用线段依次连结起来,所得的图案与原图案相比有何变化?
(2)横坐标不变,纵坐标分别乘以-1,再将所得的各个点用线段依次连结起来,所得的图案又与原图案相比有何变化?根据活动结果,并回答:
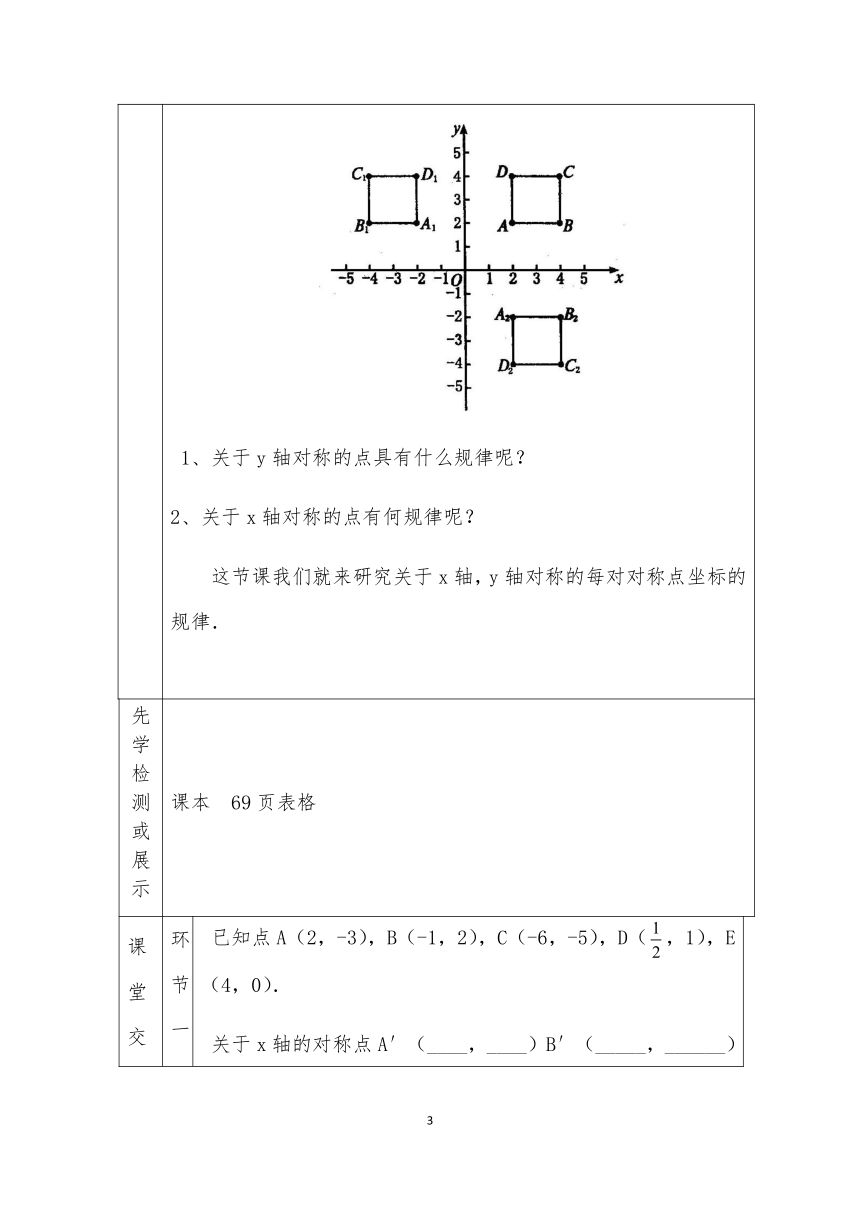
1、关于y轴对称的点具有什么规律呢?
2、关于x轴对称的点有何规律呢?
这节课我们就来研究关于x轴,y轴对称的每对对称点坐标的规律.
先学检测或展示
课本
69页表格
课堂交互学习
环节一
已知点A(2,-3),B(-1,2),C(-6,-5),D(,1),E(4,0).
关于x轴的对称点A′(____,____)B′(_____,______)C′(_____,_____)D′(____,_____)E′(_____,_____).
关于y轴的对称点A″(_____,____)B″(_____,______)C″(_____,_____)D″(____,_____)E″(_____,_____).
环节二
先在坐标系中作出A点关于x轴的对称点,即过A作x轴的垂线交x轴于M点,M点的坐标为(2,0).在AM的延长线上截A′M=AM,则A′就是A点关于x轴的对称点,所以A′在第一象限,因为A′M=AM,所以A′的纵坐标为3,因为AA′⊥x轴,即AA′∥y轴,所以A′的横坐标为2,即A′的坐标为(2,3).
已知点
A(2,-3)B(-1,2)C(-6,-5)关于x轴的对称点A′(2,3)B′(-1,-2)
C′(-6,5)已知点D(,1)E(4,0)关于x轴的对称点D′(,-1)
E′(4,0)
同样,我们先作出A关于y轴的对称点A″,并求出A″的坐标.
过A作y轴的垂线AN,垂足为N,则N点坐标为(0,-3),然后在AN的延长线上截A″N,使A″N=AN,则A″就是所求的A关于y轴的对称点.A″在第三象限,AA″⊥y轴,且AN=A″N,所以A″的坐标为(-2,-3),同理可求得B,C,D,E关于y轴的对称点B″,C″,D″,E″的坐标分别为B″(1,2),C″(6,-5),D″(-,1),E″(-4,0).列表如下:
已知点
A(2,-3)B(-1,2)C(-6,-5)
关于y轴对称点A″(-2,-3)
B″(1,2)C″(6,-5)
已知点
D(,1)E(4,0)
关于y轴对称点D″(,1)E″(-4,0)
环节三
观察上表,比较每对关于y轴的对称点的坐标,你能发现什么规律?关于y轴对称的每一对对称点的坐标纵坐标相同,横坐标互为相反数.
整体达标检测
第70页
例2
拓展巩固练习
第71页
练习2
教学反思
用坐标表示轴对称
课型
新授课
总课时
教学目标
1.在平面直角坐标系中,探索关于x轴、y轴对称的点的坐标规律.
2.利用关于x轴、y轴对称的点的坐标的规律,能作出关于x轴、y轴对称的图形.
3.在用坐标表示轴对称时发展形象思维能力和数形结合的意识.
教学过程
先行独立学习
已知点A(2,-3),B(-1,2),C(-6,-5),D(,1),E(4,0).
关于x轴的对称点A′(____,____)B′(_____,______)C′(_____,_____)D′(____,_____)E′(_____,_____).
关于y轴的对称点A″(_____,____)B″(_____,______)C″(_____,_____)D″(____,_____)E″(_____,_____).
迁移导入
在平面直角坐标系中,将坐标为(2,2),(4,2),(4,4),(2,4),(2,2)的点用线段依次连结起来形成一个图案.
(1)纵坐标不变,横坐标分别乘以-1,再将所得的各个点用线段依次连结起来,所得的图案与原图案相比有何变化?
(2)横坐标不变,纵坐标分别乘以-1,再将所得的各个点用线段依次连结起来,所得的图案又与原图案相比有何变化?根据活动结果,并回答:
1、关于y轴对称的点具有什么规律呢?
2、关于x轴对称的点有何规律呢?
这节课我们就来研究关于x轴,y轴对称的每对对称点坐标的规律.
先学检测或展示
课本
69页表格
课堂交互学习
环节一
已知点A(2,-3),B(-1,2),C(-6,-5),D(,1),E(4,0).
关于x轴的对称点A′(____,____)B′(_____,______)C′(_____,_____)D′(____,_____)E′(_____,_____).
关于y轴的对称点A″(_____,____)B″(_____,______)C″(_____,_____)D″(____,_____)E″(_____,_____).
环节二
先在坐标系中作出A点关于x轴的对称点,即过A作x轴的垂线交x轴于M点,M点的坐标为(2,0).在AM的延长线上截A′M=AM,则A′就是A点关于x轴的对称点,所以A′在第一象限,因为A′M=AM,所以A′的纵坐标为3,因为AA′⊥x轴,即AA′∥y轴,所以A′的横坐标为2,即A′的坐标为(2,3).
已知点
A(2,-3)B(-1,2)C(-6,-5)关于x轴的对称点A′(2,3)B′(-1,-2)
C′(-6,5)已知点D(,1)E(4,0)关于x轴的对称点D′(,-1)
E′(4,0)
同样,我们先作出A关于y轴的对称点A″,并求出A″的坐标.
过A作y轴的垂线AN,垂足为N,则N点坐标为(0,-3),然后在AN的延长线上截A″N,使A″N=AN,则A″就是所求的A关于y轴的对称点.A″在第三象限,AA″⊥y轴,且AN=A″N,所以A″的坐标为(-2,-3),同理可求得B,C,D,E关于y轴的对称点B″,C″,D″,E″的坐标分别为B″(1,2),C″(6,-5),D″(-,1),E″(-4,0).列表如下:
已知点
A(2,-3)B(-1,2)C(-6,-5)
关于y轴对称点A″(-2,-3)
B″(1,2)C″(6,-5)
已知点
D(,1)E(4,0)
关于y轴对称点D″(,1)E″(-4,0)
环节三
观察上表,比较每对关于y轴的对称点的坐标,你能发现什么规律?关于y轴对称的每一对对称点的坐标纵坐标相同,横坐标互为相反数.
整体达标检测
第70页
例2
拓展巩固练习
第71页
练习2
教学反思
