人教版八年级数学上册课时练 : 13.2 画轴对称图形(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学上册课时练 : 13.2 画轴对称图形(Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 516.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-19 23:30:12 | ||
图片预览



文档简介
人教版八年级数学上册课时练
第十三章
轴对称
13.2
画轴对称图形
一、选择题
1.如图,点P在∠MON的内部,点P关于OM,ON的对称点分别为A,B,连接AB,交OM于点C,交ON于点D,连接PC,PD.若∠MON=50°,则∠CPD=( )
A.70°
B.80°
C.90°
D.100°
2.如图,已知等边△ABC的面积为4,
P、Q、R分别为边AB、BC、AC上的动点,则PR+QR的最小值是(
)
A.3
B.2
C.
D.4
3.已知,为内一定点,上有一点,上有一点,当的周长取最小值时,的度数是
A.
B.
C.
D.
4.如图,,为内部一条射线,点为射线上一点,为,点、分别为射线、上的动点,则周长的最小值是(
)
A.
B.2
C.
D.4
5.在坐标平面上有一个轴对称图形,其中A(3,﹣)和B(3,﹣)是图形上的一对对称点,若此图形上另有一点C(﹣2,﹣9),则C点对称点的坐标是( )
A.(﹣2,1)
B.(﹣2,﹣)
C.(﹣,﹣9)
D.(﹣2,﹣1)
6.如图,,点是内的一定点,点分别在上移动,当的周长最小时,的值为(
)
A.
B.
C.
D.
7.如图,在锐角△ABC?中,AC=10,S△ABC
=25,∠BAC?的平分线交?BC?于点?D,点?M,N?分别是?AD?和?AB?上的动点,则?BM+MN?的最小值是(
)
A.4
B.
C.5
D.6
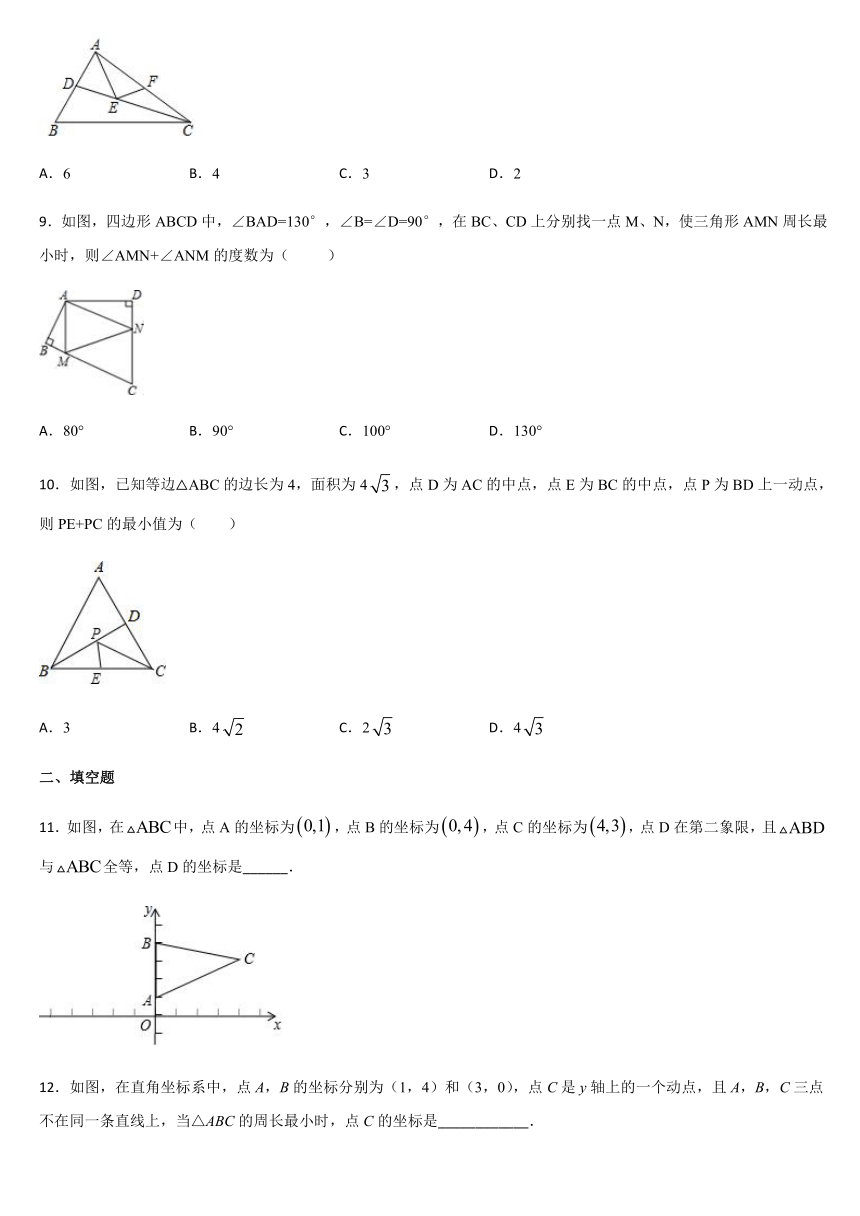
8.如图,CD是△ABC的角平分线,△ABC的面积为12,BC长为6,点E,F分别是CD,AC上的动点,则AE+EF的最小值是( )
A.6
B.4
C.3
D.2
9.如图,四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使三角形AMN周长最小时,则∠AMN+∠ANM的度数为(
)
A.80°
B.90°
C.100°
D.130°
10.如图,已知等边△ABC的边长为4,面积为4,点D为AC的中点,点E为BC的中点,点P为BD上一动点,则PE+PC的最小值为( )
A.3
B.4
C.2
D.4
二、填空题
11.如图,在中,点A的坐标为,点B的坐标为,点C的坐标为,点D在第二象限,且与全等,点D的坐标是______.
12.如图,在直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是____________.
13.如图,∠AOB=30°,内有一点P且OP=5,若M、N为边OA、OB上两动点,那么△PMN的周长最小为__________.
14.如图,点P是∠AOB内任意一点,OP=4cm,点M和点N分别是射线OA和射线OB上的动点,∠AOB=30°则△PMN周长的最小值=________
.
15.如图,△ABC是边长为1的等边三角形,BD为AC边上的高,将△ABC折叠,使点B与点D重合,折痕EF交BD于点D1,再将△BEF折叠,使点B于点D1重合,折痕GH交BD1于点D2,依次折叠,则BDn=
.
三、解答题
16.如图所示,点P在∠AOB内,点M、N分别是点P关于AO、BO所在直线的对称点.
(1)若△PEF的周长为20,求MN的长.
(2)若∠O=50°,求∠EPF的度数.
(3)请直接写出∠EPF与∠O的数量关系是_____________________________
17.(阅读)如图1,四边形中,,,,,经过点的直线将四边形分成两部分,直线与所成的角设为,将四边形的直角沿直线折叠,点落在点处,我们把这个操作过程记为.
(理解)若点与点重合,则这个操作过程为[__________,__________];
(尝试)
(1)若点恰为的中点(如图2),求;
(2)经过操作,点落在处,若点在四边形的边上(如图3),求出的值.
18.如图,∠AOB=30°,点P是∠AOB内一点,PO=8,在∠AOB的两边分别有点R、Q(均不同于O),求△PQR周长的最小值.
19.在一平直河岸l同侧有A,B两个村庄,A,B到l的距离分别是3km和2km,AB=akm(a>1).现计划在河岸l上建一抽水站P,用输水管向两个村庄供水.
方案设计
某班数学兴趣小组设计了两种铺设管道方案:图1是方案一的示意图,设该方案中管道长度为d1,且d1=PB+BA(km)(其中BP⊥l于点P);图2是方案二的示意图,设该方案中管道长度为d2,且d2=PA+PB(km)(其中点A′与点A关于l对称,A′B与l交于点P).
观察计算
(1)在方案一中,d1=
km(用含a的式子表示)
(2)在方案二中,组长小宇为了计算d2的长,作了如图3所示的辅助线,请你按小宇同学的思路计算,d2=
km(用含a的式子表示).
探索归纳
(1)①当a=4时,比较大小:d1
d2(填“>”、“=”或“<”);②当a=6时,比较大小:d1
d2(填“>”、“=”或“<”);
(2)请你参考方框中的方法指导,就a(当a>1时)的所有取值情况进行分析,要使铺设的管道长度较短,应选择方案一还是方案二?
20.如图1,在长方形纸片ABCD中,E点在边AD上,F、G分别在边AB、CD上,分别以EF、EG为折痕进行折叠并压平,点A、D的对应点分别是点A′和点D′,
(1)如图2中A′落在ED′上,求∠FEG的度数;
(2)如图3中∠A′ED′=50°,求∠FEG的度数;
(3)如图4中∠FEG=85°,请直接写出∠A′ED′的度数;
(4)若∠A′ED'=n°,直接写出∠FEG的度数(用含n的代数式表示).
21.几何模型:
条件:如图1,A、B是直线同旁的两个定点.
问题:在直线上确定一点P,使PA+PB的值最小.
方法:作点A关于直线的对称点A′,连接A′B交于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
(1)如图2,已知平面直角坐标系中两定点A(0,-1),B(2,-1),P为x轴上一动点,
则当PA+PB的值最小时,点P的横坐标是______,此时PA+PB的最小值是______;
(2)如图3,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.由正方形对称性可知,B与D关于直线AC对称,连接BD,则PB+PE的最小值是______;
(3)如图4,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一动点P,则PD+PE的最小值为
;
(4)如图5,在菱形ABCD中,AB=8,∠B=60°,点G是边CD边的中点,点E、F分别是AG、AD上的两个动点,则EF+ED的最小值是_______________.
22.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)若△A1B1C1与△ABC关于y轴成轴对称,则△A1B1C1三个顶点坐标分别为A1_____,B1_____,C1_____
(2)在y轴上是否存在点Q.使得S△ACQ=S△ABC,如果存在,求出点Q的坐标,如果不存在,说明理由;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标是_____.
23.如图,将矩形OABC放在平面直角坐标系中,O为原点,点A在x轴的正半轴上,B(8,6),点D是射线AO上的一点,把△BAD沿直线BD折叠,点A的对应点为A′.
(1)若点A′落在矩形的对角线OB上时,OA′的长=
;
(2)若点A′落在边AB的垂直平分线上时,求点D的坐标;
(3)若点A′落在边AO的垂直平分线上时,求点D的坐标(直接写出结果即可).
【参考答案】
1.B
2.B
3.C
4.B
5.A
6.D
7.C
8.B
9.C
10.C
11.(-4,2)或(-4,3)
12.(0,3)
13.5
14.4cm
15..
16.(1)20;(2)80°;(3)∠EPF=
180°-2∠O
17.;(1)30°;(2)5
18.8
19.观察计算:(1)a+2;(2);探索归纳:(1)①<,②>;(2)当a>5时,选方案二;当a=5时,选方案一或方案二;当1<a<5时,选方案一.
20.(1)∠FEG=90°;(2)∠FEG=115°;(3)∠A′ED′=10°;(4)∠FEG的度数为或.
21.(1)点P的横坐标是
1
,此时PA+PB的最小值是;(2)PB+PE的最小值是
(3)这个最小值为
;(4)EF+ED的最小值是
22.(﹣1,1)
(﹣4,2)
(﹣3,4)
(2,0)
23.(1)4;(2)点D(8﹣2,0);(3)点D的坐标为(3﹣1,0)或(﹣3﹣1,0).
第十三章
轴对称
13.2
画轴对称图形
一、选择题
1.如图,点P在∠MON的内部,点P关于OM,ON的对称点分别为A,B,连接AB,交OM于点C,交ON于点D,连接PC,PD.若∠MON=50°,则∠CPD=( )
A.70°
B.80°
C.90°
D.100°
2.如图,已知等边△ABC的面积为4,
P、Q、R分别为边AB、BC、AC上的动点,则PR+QR的最小值是(
)
A.3
B.2
C.
D.4
3.已知,为内一定点,上有一点,上有一点,当的周长取最小值时,的度数是
A.
B.
C.
D.
4.如图,,为内部一条射线,点为射线上一点,为,点、分别为射线、上的动点,则周长的最小值是(
)
A.
B.2
C.
D.4
5.在坐标平面上有一个轴对称图形,其中A(3,﹣)和B(3,﹣)是图形上的一对对称点,若此图形上另有一点C(﹣2,﹣9),则C点对称点的坐标是( )
A.(﹣2,1)
B.(﹣2,﹣)
C.(﹣,﹣9)
D.(﹣2,﹣1)
6.如图,,点是内的一定点,点分别在上移动,当的周长最小时,的值为(
)
A.
B.
C.
D.
7.如图,在锐角△ABC?中,AC=10,S△ABC
=25,∠BAC?的平分线交?BC?于点?D,点?M,N?分别是?AD?和?AB?上的动点,则?BM+MN?的最小值是(
)
A.4
B.
C.5
D.6
8.如图,CD是△ABC的角平分线,△ABC的面积为12,BC长为6,点E,F分别是CD,AC上的动点,则AE+EF的最小值是( )
A.6
B.4
C.3
D.2
9.如图,四边形ABCD中,∠BAD=130°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使三角形AMN周长最小时,则∠AMN+∠ANM的度数为(
)
A.80°
B.90°
C.100°
D.130°
10.如图,已知等边△ABC的边长为4,面积为4,点D为AC的中点,点E为BC的中点,点P为BD上一动点,则PE+PC的最小值为( )
A.3
B.4
C.2
D.4
二、填空题
11.如图,在中,点A的坐标为,点B的坐标为,点C的坐标为,点D在第二象限,且与全等,点D的坐标是______.
12.如图,在直角坐标系中,点A,B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A,B,C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是____________.
13.如图,∠AOB=30°,内有一点P且OP=5,若M、N为边OA、OB上两动点,那么△PMN的周长最小为__________.
14.如图,点P是∠AOB内任意一点,OP=4cm,点M和点N分别是射线OA和射线OB上的动点,∠AOB=30°则△PMN周长的最小值=________
.
15.如图,△ABC是边长为1的等边三角形,BD为AC边上的高,将△ABC折叠,使点B与点D重合,折痕EF交BD于点D1,再将△BEF折叠,使点B于点D1重合,折痕GH交BD1于点D2,依次折叠,则BDn=
.
三、解答题
16.如图所示,点P在∠AOB内,点M、N分别是点P关于AO、BO所在直线的对称点.
(1)若△PEF的周长为20,求MN的长.
(2)若∠O=50°,求∠EPF的度数.
(3)请直接写出∠EPF与∠O的数量关系是_____________________________
17.(阅读)如图1,四边形中,,,,,经过点的直线将四边形分成两部分,直线与所成的角设为,将四边形的直角沿直线折叠,点落在点处,我们把这个操作过程记为.
(理解)若点与点重合,则这个操作过程为[__________,__________];
(尝试)
(1)若点恰为的中点(如图2),求;
(2)经过操作,点落在处,若点在四边形的边上(如图3),求出的值.
18.如图,∠AOB=30°,点P是∠AOB内一点,PO=8,在∠AOB的两边分别有点R、Q(均不同于O),求△PQR周长的最小值.
19.在一平直河岸l同侧有A,B两个村庄,A,B到l的距离分别是3km和2km,AB=akm(a>1).现计划在河岸l上建一抽水站P,用输水管向两个村庄供水.
方案设计
某班数学兴趣小组设计了两种铺设管道方案:图1是方案一的示意图,设该方案中管道长度为d1,且d1=PB+BA(km)(其中BP⊥l于点P);图2是方案二的示意图,设该方案中管道长度为d2,且d2=PA+PB(km)(其中点A′与点A关于l对称,A′B与l交于点P).
观察计算
(1)在方案一中,d1=
km(用含a的式子表示)
(2)在方案二中,组长小宇为了计算d2的长,作了如图3所示的辅助线,请你按小宇同学的思路计算,d2=
km(用含a的式子表示).
探索归纳
(1)①当a=4时,比较大小:d1
d2(填“>”、“=”或“<”);②当a=6时,比较大小:d1
d2(填“>”、“=”或“<”);
(2)请你参考方框中的方法指导,就a(当a>1时)的所有取值情况进行分析,要使铺设的管道长度较短,应选择方案一还是方案二?
20.如图1,在长方形纸片ABCD中,E点在边AD上,F、G分别在边AB、CD上,分别以EF、EG为折痕进行折叠并压平,点A、D的对应点分别是点A′和点D′,
(1)如图2中A′落在ED′上,求∠FEG的度数;
(2)如图3中∠A′ED′=50°,求∠FEG的度数;
(3)如图4中∠FEG=85°,请直接写出∠A′ED′的度数;
(4)若∠A′ED'=n°,直接写出∠FEG的度数(用含n的代数式表示).
21.几何模型:
条件:如图1,A、B是直线同旁的两个定点.
问题:在直线上确定一点P,使PA+PB的值最小.
方法:作点A关于直线的对称点A′,连接A′B交于点P,则PA+PB=A′B的值最小(不必证明).
模型应用:
(1)如图2,已知平面直角坐标系中两定点A(0,-1),B(2,-1),P为x轴上一动点,
则当PA+PB的值最小时,点P的横坐标是______,此时PA+PB的最小值是______;
(2)如图3,正方形ABCD的边长为2,E为AB的中点,P是AC上一动点.由正方形对称性可知,B与D关于直线AC对称,连接BD,则PB+PE的最小值是______;
(3)如图4,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一动点P,则PD+PE的最小值为
;
(4)如图5,在菱形ABCD中,AB=8,∠B=60°,点G是边CD边的中点,点E、F分别是AG、AD上的两个动点,则EF+ED的最小值是_______________.
22.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)若△A1B1C1与△ABC关于y轴成轴对称,则△A1B1C1三个顶点坐标分别为A1_____,B1_____,C1_____
(2)在y轴上是否存在点Q.使得S△ACQ=S△ABC,如果存在,求出点Q的坐标,如果不存在,说明理由;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标是_____.
23.如图,将矩形OABC放在平面直角坐标系中,O为原点,点A在x轴的正半轴上,B(8,6),点D是射线AO上的一点,把△BAD沿直线BD折叠,点A的对应点为A′.
(1)若点A′落在矩形的对角线OB上时,OA′的长=
;
(2)若点A′落在边AB的垂直平分线上时,求点D的坐标;
(3)若点A′落在边AO的垂直平分线上时,求点D的坐标(直接写出结果即可).
【参考答案】
1.B
2.B
3.C
4.B
5.A
6.D
7.C
8.B
9.C
10.C
11.(-4,2)或(-4,3)
12.(0,3)
13.5
14.4cm
15..
16.(1)20;(2)80°;(3)∠EPF=
180°-2∠O
17.;(1)30°;(2)5
18.8
19.观察计算:(1)a+2;(2);探索归纳:(1)①<,②>;(2)当a>5时,选方案二;当a=5时,选方案一或方案二;当1<a<5时,选方案一.
20.(1)∠FEG=90°;(2)∠FEG=115°;(3)∠A′ED′=10°;(4)∠FEG的度数为或.
21.(1)点P的横坐标是
1
,此时PA+PB的最小值是;(2)PB+PE的最小值是
(3)这个最小值为
;(4)EF+ED的最小值是
22.(﹣1,1)
(﹣4,2)
(﹣3,4)
(2,0)
23.(1)4;(2)点D(8﹣2,0);(3)点D的坐标为(3﹣1,0)或(﹣3﹣1,0).
