人教版数学八年级上册 14.1.1 同底数幂的乘法 同步课时练习 (Word版 含答案)
文档属性
| 名称 | 人教版数学八年级上册 14.1.1 同底数幂的乘法 同步课时练习 (Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 16.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-19 00:00:00 | ||
图片预览


文档简介
第14章
整式的乘法与因式分解
14.1
整式的乘法
14.1.1
同底数幂的乘法
一、单项选择题
1.下列各式的结果等于26的是(
)
A.2+25
B.2·25
C.23·25
D.0.22·
0.24
2.下列计算结果正确的是(
)
A.
a3
·a3=a9
B.
m2·n2=mn4
C.
xm·x3=x3m
D.
y·yn=yn+1
二、填空题
3.
用科学记数法表示下列各数:
(1)10000=_______;
(2)1亿=___________.
4.
填空:
(1)x·x2·x(
)=x7;
(2)xm·(
)=x3m;
(3)8×4=2x,则x=(
).
5.
计算:
(1)-2×(-2)=_________;
(2)(-3)×3×(-1)×(-7)=__________.
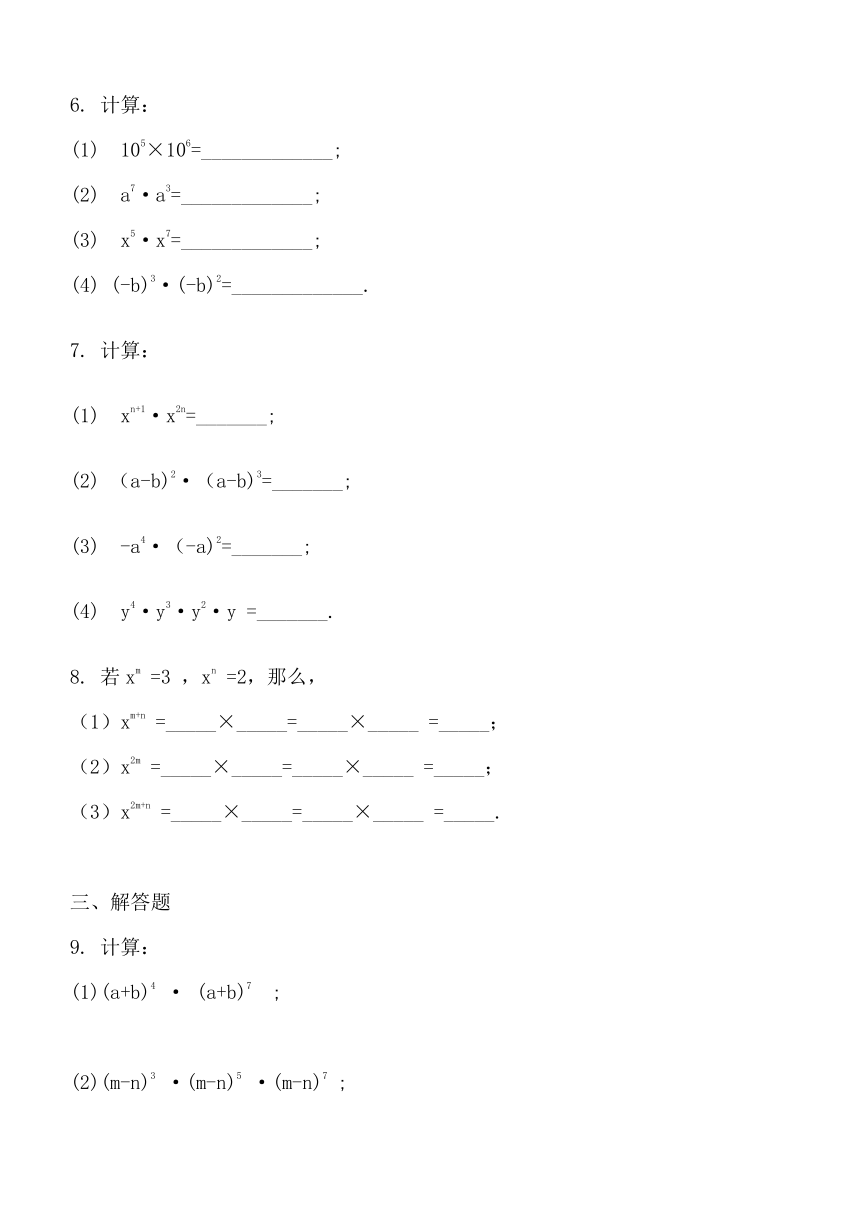
6.
计算:
(1)
105×106=_____________;
(2)
a7·a3=_____________;
(3)
x5·x7=_____________;
(4)
(-b)3·(-b)2=_____________.
7.
计算:
(1)
xn+1·x2n=_______;
(2)
(a-b)2·(a-b)3=_______;
(3)
-a4·(-a)2=_______;
(4)
y4·y3·y2·y
=_______.
8.
若xm
=3
,xn
=2,那么,
(1)xm+n
=_____×_____=_____×_____
=_____;
(2)x2m
=_____×_____=_____×_____
=_____;
(3)x2m+n
=_____×_____=_____×_____
=_____.
三、解答题
9.
计算:
(1)(a+b)4
·
(a+b)7
;
(2)(m-n)3
·(m-n)5
·(m-n)7
;
(3)(x-y)2·(y-x)5.
10.
计算下列各题:
(1)(2a+b)2n+1·(2a+b)3;
(2)(a-b)3·(b-a)4;
(3)
(-3)×(-3)2
×(-3)3;
(4)-a3·(-a)2·(-a)3.
11.
若xa=3,xb=4,xc=5,求2xa+b+c的值.
12.
已知23x+2=32,求x的值.
13.
已知xa=8,xb=9,求xa+b的值.
14.
已知an-3·a2n+1=a10,求n的值;
15.
3×27×9
=
32x-4,求x的值;
16.
下面的计算对不对?如果不对,应当怎样改正.
(1)b3·b3=2b3
(2)b3+b3=b6
(3)a·a5·a3=a8
(4)(-x)4·(-x)4=(-x)16
17.
am+n可以写成哪两个因式的积?
答案:
一、
1.
B
2.
D
二、
3.
(1)
1×104
(2)
1×108
4.
(1)
4
(2)
x2m
(3)
5
5.
(1)
4
(2)
-63
6.
(1)
1011
(2)
a10
(3)
x12
(4)
(-b)5=-b5
7.
(1)
x3n+1
(2)
(a-b)5
(3)
-a6
(4)
y10
8.
(1)
xm
xn
3
2
6
(2)
xm
xm
3
3
9
(3)
x2m
xn
9
2
18
三、
9.
解:(1)
(a+b)4
·
(a+b)7
=
(a+b)4+7
=(a+b)11;
(2)(m-n)3
·(m-n)5
·(m-n)7
=(m-n)3+5+7=(m-n)15;
(3)(x-y)2·(y-x)5=(y-x)2(y-x)5=(y-x)2+5=(y-x)7.
10.
解:(1)(2a+b)2n+1·(2a+b)3=(2a+b)2n+4;
(2)(a-b)3·(b-a)4=(a-b)7;
(3)
(-3)×(-3)2
×(-3)3=36;
(4)-a3·(-a)2·(-a)3=a8.
11.
解:2xa+b+c=2xa·xb·xc=120.
12.
解:∵
23x+2=32=25,
∴3x+2=5,
∴x=1.
13.
解:xa+b=xa·xb=8×9=72;
14.
解:n-3+2n+1=10,
n=4;
15.
解:3×27×9
=3×33×32=32x-4,
2x-4=6;
x=5.
16.
解:(1)
×
b6
(2)
×
2b3
(3)
×
a9
(4)
×
(-x)8=x8
17.
am+n
=
am
·
an
整式的乘法与因式分解
14.1
整式的乘法
14.1.1
同底数幂的乘法
一、单项选择题
1.下列各式的结果等于26的是(
)
A.2+25
B.2·25
C.23·25
D.0.22·
0.24
2.下列计算结果正确的是(
)
A.
a3
·a3=a9
B.
m2·n2=mn4
C.
xm·x3=x3m
D.
y·yn=yn+1
二、填空题
3.
用科学记数法表示下列各数:
(1)10000=_______;
(2)1亿=___________.
4.
填空:
(1)x·x2·x(
)=x7;
(2)xm·(
)=x3m;
(3)8×4=2x,则x=(
).
5.
计算:
(1)-2×(-2)=_________;
(2)(-3)×3×(-1)×(-7)=__________.
6.
计算:
(1)
105×106=_____________;
(2)
a7·a3=_____________;
(3)
x5·x7=_____________;
(4)
(-b)3·(-b)2=_____________.
7.
计算:
(1)
xn+1·x2n=_______;
(2)
(a-b)2·(a-b)3=_______;
(3)
-a4·(-a)2=_______;
(4)
y4·y3·y2·y
=_______.
8.
若xm
=3
,xn
=2,那么,
(1)xm+n
=_____×_____=_____×_____
=_____;
(2)x2m
=_____×_____=_____×_____
=_____;
(3)x2m+n
=_____×_____=_____×_____
=_____.
三、解答题
9.
计算:
(1)(a+b)4
·
(a+b)7
;
(2)(m-n)3
·(m-n)5
·(m-n)7
;
(3)(x-y)2·(y-x)5.
10.
计算下列各题:
(1)(2a+b)2n+1·(2a+b)3;
(2)(a-b)3·(b-a)4;
(3)
(-3)×(-3)2
×(-3)3;
(4)-a3·(-a)2·(-a)3.
11.
若xa=3,xb=4,xc=5,求2xa+b+c的值.
12.
已知23x+2=32,求x的值.
13.
已知xa=8,xb=9,求xa+b的值.
14.
已知an-3·a2n+1=a10,求n的值;
15.
3×27×9
=
32x-4,求x的值;
16.
下面的计算对不对?如果不对,应当怎样改正.
(1)b3·b3=2b3
(2)b3+b3=b6
(3)a·a5·a3=a8
(4)(-x)4·(-x)4=(-x)16
17.
am+n可以写成哪两个因式的积?
答案:
一、
1.
B
2.
D
二、
3.
(1)
1×104
(2)
1×108
4.
(1)
4
(2)
x2m
(3)
5
5.
(1)
4
(2)
-63
6.
(1)
1011
(2)
a10
(3)
x12
(4)
(-b)5=-b5
7.
(1)
x3n+1
(2)
(a-b)5
(3)
-a6
(4)
y10
8.
(1)
xm
xn
3
2
6
(2)
xm
xm
3
3
9
(3)
x2m
xn
9
2
18
三、
9.
解:(1)
(a+b)4
·
(a+b)7
=
(a+b)4+7
=(a+b)11;
(2)(m-n)3
·(m-n)5
·(m-n)7
=(m-n)3+5+7=(m-n)15;
(3)(x-y)2·(y-x)5=(y-x)2(y-x)5=(y-x)2+5=(y-x)7.
10.
解:(1)(2a+b)2n+1·(2a+b)3=(2a+b)2n+4;
(2)(a-b)3·(b-a)4=(a-b)7;
(3)
(-3)×(-3)2
×(-3)3=36;
(4)-a3·(-a)2·(-a)3=a8.
11.
解:2xa+b+c=2xa·xb·xc=120.
12.
解:∵
23x+2=32=25,
∴3x+2=5,
∴x=1.
13.
解:xa+b=xa·xb=8×9=72;
14.
解:n-3+2n+1=10,
n=4;
15.
解:3×27×9
=3×33×32=32x-4,
2x-4=6;
x=5.
16.
解:(1)
×
b6
(2)
×
2b3
(3)
×
a9
(4)
×
(-x)8=x8
17.
am+n
=
am
·
an
