人教版数学九年级上册课件:22.2 二次函数与一元二次方程(21张)
文档属性
| 名称 | 人教版数学九年级上册课件:22.2 二次函数与一元二次方程(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-19 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
你投过
篮
吗
?
22.2
二次函数与一元二次方程
(第一课时)
x=
2
y=-2x+4
2
4
x
y
0
复习引入
归纳:
一次函数y=kx+b(k≠0)的图象和x轴交点的横坐标与一元一次方程kx+b=0的解是密切联系的!
思考:
根据图像,你知道一元一次方程-2x+4=0的解是多少吗?
问题:如图,以40m/s的速度将小球沿与地面成300角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气的阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有如下关系:h=20t-5t2,请同学们考虑以下问题:
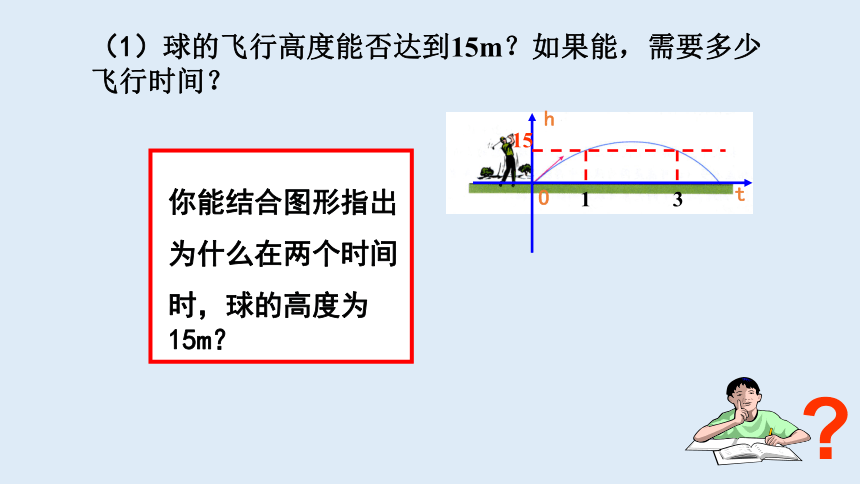
(1)球的飞行高度能否达到15m?如果能,需要多少飞行时间?
(1)球的飞行高度能否达到15m?如果能,需要多少飞行时间?
你能结合图形指出
为什么在两个时间
时,球的高度为15m?
O
h
t
15
1
3
?
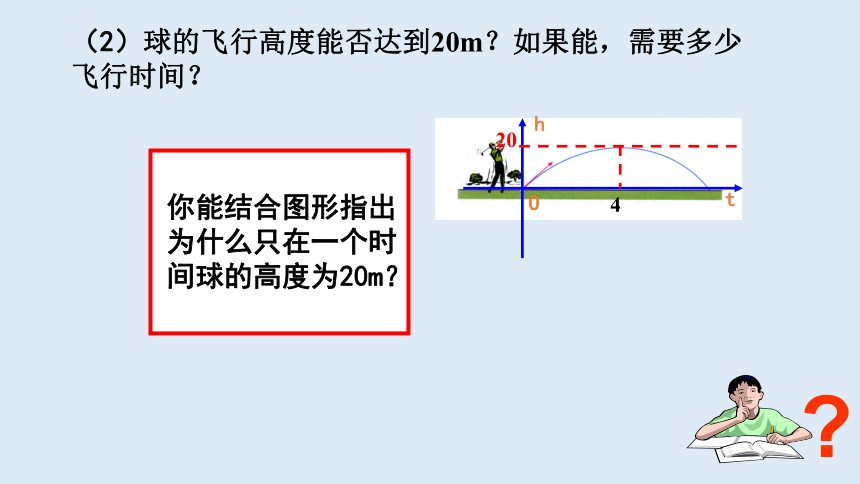
(2)球的飞行高度能否达到20m?如果能,需要多少飞行时间?
你能结合图形指出为什么只在一个时间球的高度为20m?
O
h
t
20
4
?
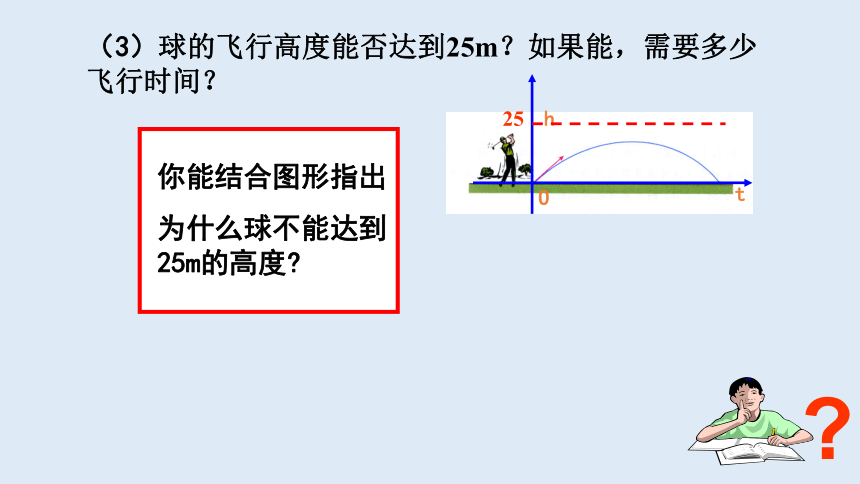
(3)球的飞行高度能否达到25m?如果能,需要多少飞行时间?
O
h
t
你能结合图形指出
为什么球不能达到25m的高度?
25
?
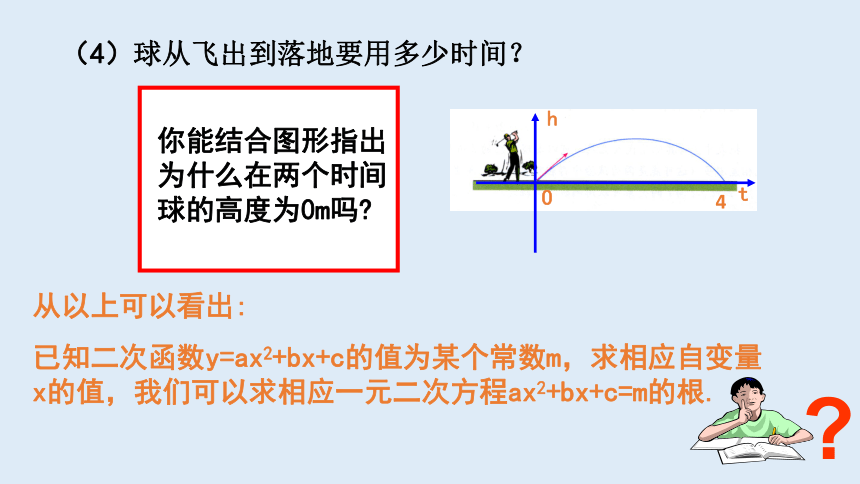
(4)球从飞出到落地要用多少时间?
你能结合图形指出为什么在两个时间球的高度为0m吗?
O
h
t
?
4
从以上可以看出:
已知二次函数y=ax2+bx+c的值为某个常数m,求相应自变量x的值,我们可以求相应一元二次方程ax2+bx+c=m的根.
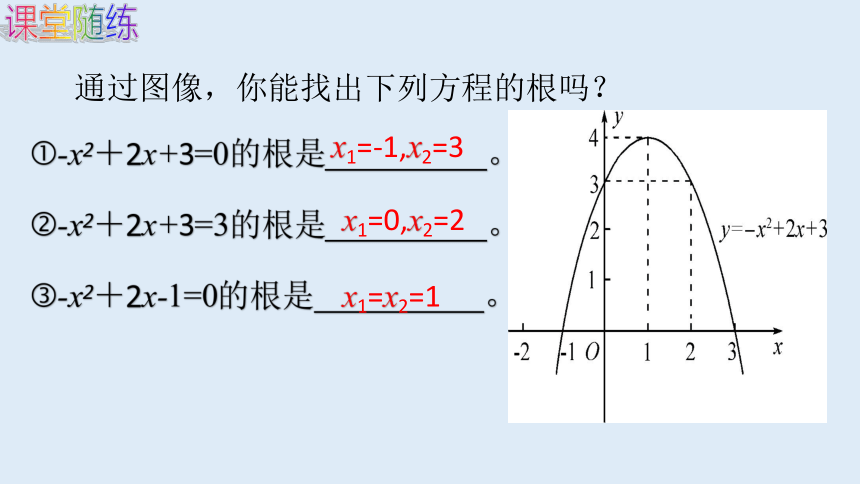
课堂随练
通过图像,你能找出下列方程的根吗?
?-x2+2x+3=0的根是
。
?-x2+2x+3=3的根是
。
?-x2+2x-1=0的根是
。
x1=-1,x2=3
x1=0,x2=2
x1=x2=1
从以上可以看出:
当求一元二次方程ax2+bx+c=m的根时,我们也可以找到相应二次函数y=ax2+bx+c的图像,令它的函数值y为常数m,求出自变量x的值。
所以二次函数和一元二次方程是密切联系的!
同学们,还想更深入的探究二次函数与一元二次方程的联系吗?
跟我走吧!
思考
下列二次函数的图象与x轴有公共点吗?如果有,公共点的横坐标是多少?当x取公共点的横坐标时,函数y的值是多少?由此,你能得出相应的一元二次方程的根吗?
(2)y
=
x2-6x+9
(3)y
=
x2-x+1
x2+x-2=0
(1)y
=
x2+x-2
x2-6x+9=0
x2-x+1=0
二次函数
y=ax2+bx+c
与x轴的交点个数
图象(a≠0)
(假定a>0)
一元二次方程ax2+bx+c=0
(a≠0)的根的情况
判别式:
△=b2-4ac
x
y
O
与x轴有两个不
同的交点
有两个不相等的实数根
△>0
x
y
O
与x轴有唯一的一个交点
有两个相等的
实数根
△
=
0
x
y
O
与x轴没有交点
没有实数根
△<0
归纳总结
1.二次函数y=x2+4x+5的图像与x轴的交点个数是
个.
0
牛刀小试
2.二次函数y=ax2+bx+c的值永远为负值的条件是(
)
A.a>0,b2-4ac<0 B.a<0,b2-4ac>0
C.a>0,b2-4ac>0
D.a<0,b2-4ac<0
D
牛刀小试
3.已知二次函数
(1)求证:此二次函数的图像与x轴有两个不同的交点.
(2)若二次函数的图像与x轴的两个交点中,其中一个点的交点坐标为(1,0),求另外一个交点坐标.
亮剑
-2
y
x
1
y=x2+x-2
(3)在(2)的条件下,此抛物线与直线y=-2、y=x-1有交点吗?若有,交点坐标是多少?
拓展
-2
-2
y
x
1
y=x2+x-2
y=-2
-2
y=x-1
归纳:如何判断一条抛物线与直线y=m、y=kx+b是否有交点?(m、k、b均为常数,k≠0)
拓展
两个角度考虑:
?
数
?形
在(2)的条件下,请利用图像回答:
?x取什么值时,y>0;
?x取什么值时,y<0;
?x取什么值时,y≤-2.
课外思考
-2
y
x
1
y=x2+x-2
谈谈你的收获
小
结
(2)二次函数y=ax2+bx+c的图象与x轴的位置关系有三种:没有公共点,有一个公共点,有两个公共点,这对应着一元二次方程ax2+bx+c=0的根的三种情况:没有实数根(△<0),两个相等的实数根(△=0),有两个不等的实数根(△>0).
一般地,从二次函数y=ax2+bx+c(a
≠
0)
的图象可知
(1)如果抛物线y=ax2+bx+c
与x轴有公共点,公共点的横坐标就是方程
ax2+bx+c=0
的一个根.
注意数与形的灵活应用,也就是数学上所提倡的
思想!
数形结合
送给同学们一段话
人生犹如抛物线
当你在走向人生低谷时,想想a>0时的图像,请不要泄气,坚持下去,相信你一定能走向人生的高峰!
当你在走向人生巅峰时,想想a<0时的图像,请不要骄傲,因为站的越高,摔得也越疼!
你投过
篮
吗
?
22.2
二次函数与一元二次方程
(第一课时)
x=
2
y=-2x+4
2
4
x
y
0
复习引入
归纳:
一次函数y=kx+b(k≠0)的图象和x轴交点的横坐标与一元一次方程kx+b=0的解是密切联系的!
思考:
根据图像,你知道一元一次方程-2x+4=0的解是多少吗?
问题:如图,以40m/s的速度将小球沿与地面成300角的方向击出时,球的飞行路线将是一条抛物线,如果不考虑空气的阻力,球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有如下关系:h=20t-5t2,请同学们考虑以下问题:
(1)球的飞行高度能否达到15m?如果能,需要多少飞行时间?
(1)球的飞行高度能否达到15m?如果能,需要多少飞行时间?
你能结合图形指出
为什么在两个时间
时,球的高度为15m?
O
h
t
15
1
3
?
(2)球的飞行高度能否达到20m?如果能,需要多少飞行时间?
你能结合图形指出为什么只在一个时间球的高度为20m?
O
h
t
20
4
?
(3)球的飞行高度能否达到25m?如果能,需要多少飞行时间?
O
h
t
你能结合图形指出
为什么球不能达到25m的高度?
25
?
(4)球从飞出到落地要用多少时间?
你能结合图形指出为什么在两个时间球的高度为0m吗?
O
h
t
?
4
从以上可以看出:
已知二次函数y=ax2+bx+c的值为某个常数m,求相应自变量x的值,我们可以求相应一元二次方程ax2+bx+c=m的根.
课堂随练
通过图像,你能找出下列方程的根吗?
?-x2+2x+3=0的根是
。
?-x2+2x+3=3的根是
。
?-x2+2x-1=0的根是
。
x1=-1,x2=3
x1=0,x2=2
x1=x2=1
从以上可以看出:
当求一元二次方程ax2+bx+c=m的根时,我们也可以找到相应二次函数y=ax2+bx+c的图像,令它的函数值y为常数m,求出自变量x的值。
所以二次函数和一元二次方程是密切联系的!
同学们,还想更深入的探究二次函数与一元二次方程的联系吗?
跟我走吧!
思考
下列二次函数的图象与x轴有公共点吗?如果有,公共点的横坐标是多少?当x取公共点的横坐标时,函数y的值是多少?由此,你能得出相应的一元二次方程的根吗?
(2)y
=
x2-6x+9
(3)y
=
x2-x+1
x2+x-2=0
(1)y
=
x2+x-2
x2-6x+9=0
x2-x+1=0
二次函数
y=ax2+bx+c
与x轴的交点个数
图象(a≠0)
(假定a>0)
一元二次方程ax2+bx+c=0
(a≠0)的根的情况
判别式:
△=b2-4ac
x
y
O
与x轴有两个不
同的交点
有两个不相等的实数根
△>0
x
y
O
与x轴有唯一的一个交点
有两个相等的
实数根
△
=
0
x
y
O
与x轴没有交点
没有实数根
△<0
归纳总结
1.二次函数y=x2+4x+5的图像与x轴的交点个数是
个.
0
牛刀小试
2.二次函数y=ax2+bx+c的值永远为负值的条件是(
)
A.a>0,b2-4ac<0 B.a<0,b2-4ac>0
C.a>0,b2-4ac>0
D.a<0,b2-4ac<0
D
牛刀小试
3.已知二次函数
(1)求证:此二次函数的图像与x轴有两个不同的交点.
(2)若二次函数的图像与x轴的两个交点中,其中一个点的交点坐标为(1,0),求另外一个交点坐标.
亮剑
-2
y
x
1
y=x2+x-2
(3)在(2)的条件下,此抛物线与直线y=-2、y=x-1有交点吗?若有,交点坐标是多少?
拓展
-2
-2
y
x
1
y=x2+x-2
y=-2
-2
y=x-1
归纳:如何判断一条抛物线与直线y=m、y=kx+b是否有交点?(m、k、b均为常数,k≠0)
拓展
两个角度考虑:
?
数
?形
在(2)的条件下,请利用图像回答:
?x取什么值时,y>0;
?x取什么值时,y<0;
?x取什么值时,y≤-2.
课外思考
-2
y
x
1
y=x2+x-2
谈谈你的收获
小
结
(2)二次函数y=ax2+bx+c的图象与x轴的位置关系有三种:没有公共点,有一个公共点,有两个公共点,这对应着一元二次方程ax2+bx+c=0的根的三种情况:没有实数根(△<0),两个相等的实数根(△=0),有两个不等的实数根(△>0).
一般地,从二次函数y=ax2+bx+c(a
≠
0)
的图象可知
(1)如果抛物线y=ax2+bx+c
与x轴有公共点,公共点的横坐标就是方程
ax2+bx+c=0
的一个根.
注意数与形的灵活应用,也就是数学上所提倡的
思想!
数形结合
送给同学们一段话
人生犹如抛物线
当你在走向人生低谷时,想想a>0时的图像,请不要泄气,坚持下去,相信你一定能走向人生的高峰!
当你在走向人生巅峰时,想想a<0时的图像,请不要骄傲,因为站的越高,摔得也越疼!
同课章节目录
