初中数学鲁教版九年级上册第二章直角三角形的边角关系测试题(Word版 含解析)
文档属性
| 名称 | 初中数学鲁教版九年级上册第二章直角三角形的边角关系测试题(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 165.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-19 00:00:00 | ||
图片预览



文档简介
初中数学鲁教版九年级上册第二章直角三角形的边角关系测试题
一、选择题
如图,在中,,,若,则BC的长为
A.
8
B.
12
C.
D.
在中,,,则cosA的值等于
A.
B.
C.
或
D.
或
已知为锐角,且,则的度数为
A.
B.
C.
D.
的值是
A.
B.
C.
D.
若计算器的四个键的序号如图所示,在角的度量单位为“度的状态下”用计算器求,正确的按键顺序是。
A.
B.
C.
D.
为了方便行人推车过某天桥,市政府在10m高的天桥一侧修建了40m长的斜道如图所示,我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是
A.
B.
C.
D.
若角,都是锐角,以下结论:
若,则;若,则;若,则;若,则其中正确的是
A.
B.
C.
D.
如图,的三个顶点均在格点上,则tanA的值为
A.
B.
C.
2
D.
如图是某河坝横断面示意图,AC为迎水坡,AB为背水坡,过点A作水平面的垂线AD,,设斜坡AC的坡度为,坡角为,斜坡AB的坡度为,坡角为,则下列结论正确的是
A.
B.
C.
D.
如图,小明在一条东西走向公路的O处,测得图书馆A在他的北偏东方向,且与他相距200m,则图书馆A到公路的距离AB为
A.
100m
B.
C.
D.
如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西方向,则河宽的长可以表示为
A.
米
B.
米
C.
200sin?米
D.
米
中考结束后,小明和好朋友一起前往三亚旅游.他们租住的宾馆AB坐落在坡度为:的斜坡上.宾馆AB高为129米.某天,小明在宾馆顶楼的海景房A处向外看风景,发现宾馆前有一座雕像雕像的高度忽略不计,已知雕像C距离海岸线D的距离CD为260米,与宾馆AB的水平距离为36米,远处海面上一艘即将靠岸的轮船E的俯角为则轮船E距离海岸线D的距离ED的长为米
参考数据:,
A.
262
B.
212
C.
244
D.
276
二、填空题
比较大小:______填“”、“”或“”.
计算:______.
用科学计算器计算:______
结果精确到
在中,,若于D,若,,则CD为______.
一艘货轮由西向东航行,在A处测得灯塔P在它的北偏东方向,继续航行到达B处,测得灯塔P在正南方向10海里的C处是港口,点A、B、C在一条直线上,则这艘货轮由A处到B处航行的路程为______海里结果保留根号.
如图,在热气球C上测得两建筑物A、B底部的俯角分别为和如果这时气球的垂直高度CD为90米.且点A、D、B在同一直线上,则建筑物A、B间的距离为______米.
三、计算题
在“停课不停学”期间,小明用电脑在线上课,图1是他的电脑液晶显示器的侧面图,显示屏AB可以绕O点旋转一定角度.研究表明:当眼睛E与显示屏顶端A在同一水平线上,且望向显示器屏幕形成一个俯角即望向屏幕中心P的的视线EP与水平线EA的夹角时,对保护眼睛比较好,而且显示屏顶端A与底座C的连线AC与水平线CD垂直时如图时,观看屏幕最舒适,此时测得,,液晶显示屏的宽AB为32cm.
求眼睛E与显示屏顶端A的水平距离AE;结果精确到
求显示屏顶端A与底座C的距离结果精确到
参考数据:,,,,
计算;
解不等式组.
小明和小华进行社会实践活动时,想利用所学的知识测量某旗杆AB的高度.小明站在点D处利用测倾器测得旗杄顶端A的仰角为,小华在BD之间放置一个镜子,并调整镜子的位置,当镜子恰好放在点E处时,位于点D处的小明正好在镜子中看到旗杆顶端A,此时DE的距离为米,已知测倾器的高为米.请你根据以上信息,计算旗杆AB的高度.
四、解答题
如图,在菱形ABCD中,对角线AC与BD相交于点O,过点D作交BC的延长线于点E.
求证:四边形ACED是平行四边形;
若,,求的值.
阅读下列材料:小华遇到这样一个问题:已知:如图1,在中,三边的长分别为,,,求的正切值.
小华是这样解决问题的:如图2所示,先在一个正方形网格每个小正方形的边长均为中画出格点三个顶点都在小正方形的顶点处,然后在这个正方形网格中再画一个和相似的格点,从而使问题得解.
图2中与相等的角为______,的正切值为______;
参考小华解决问题的方法,利用图4中的正方形网格每个小正方形的边长均为
解决问题:如图3,在中,,,,延长HK,求的度数.
已知,,,D是AB边上一点,连接CD,E是CD上一点,且.
如图1,若,
求证:CD平分;
求的值;
如图2,连接BE,若,求的值.
答案和解析
1.【答案】C
【解析】解:法一、在中,
,
.
.
故选:C.
法二、在中,
,
.
,
.
故选:C.
根据锐角三角函数的边角间关系,先求出AB,再利用勾股定理求出BC.
本题考查了解直角三角形.掌握直角三角形的边角间关系是解决本题的关键.
2.【答案】C
【解析】解:当为直角三角形时,存在两种情况:
当AB为斜边,,
,,
.
;
当AC为斜边,,
由勾股定理得:,
;
综上所述,cosA的值等于或.
故选:C.
因为原题没有说明哪个角是直角,所以要分情况讨论:为斜边,为斜边,根据勾股定理求得AB的值,然后根据余弦的定义即可求解.
本题考查了余弦函数的定义,理解定义是关键,并注意分类讨论.
3.【答案】C
【解析】解:为锐角,,,
.
故选:C.
根据解答即可.
此题比较简单,只要熟知特殊角度的三角函数值即可.
4.【答案】B
【解析】解:,
故选:B.
根据特殊角的三角函数值可得答案.
此题主要考查了特殊角的三角函数值,关键是掌握、、角的各种三角函数值.
5.【答案】B
【解析】
【分析】
本题考查用计算器求锐角三角函数,属于常识题,了解三角函数的计算即可求出答案.
【解答】
解:根据计算器的计算常识可知,
求的步骤为.
故选B.
6.【答案】A
【解析】解:,
所以用科学计算器求这条斜道倾斜角的度数时,按键顺序为:
故选A.
先利用正弦的定义得到,然后利用计算器求锐角.
本题考查了计算器三角函数:正确使用计算器,一般情况下,三角函数值直接可以求出,已知三角函数值求角需要用第二功能键.
7.【答案】C
【解析】解:随的增大而增大,若,则,此结论正确;
随的增大而减小,若,则,此结论错误;
随的增大而增大,若,则,此结论正确;
若,则,此结论正确;
综上,正确的结论为,
故选:C.
根据锐角范围内、、的增减性及互余两锐角的正余弦函数间的关系可得.
本题主要考查互余两锐角三角函数关系,解题的关键是掌握锐角范围内、、的增减性及互余两锐角的正余弦函数间的关系.
8.【答案】A
【解析】
【分析】
此题主要考查了解直角三角形,正确构造直角三角形是解题关键.
直接利用网格结合锐角三角函数关系得出,进而得出答案.
【解答】
解:如图所示:连接BD,
由网格可得,
则.
故选:A.
9.【答案】A
【解析】解:斜坡AC的坡度,斜坡AB的坡度,
,
,A正确,C错误;
,B错误;
,D错误;
故选:A.
根据坡度的概念分别表示出、,根据题意判断即可.
本题考查的是坡度坡角的概念,掌握坡度是坡面的铅直高度h和水平宽度l的比是解题的关键.
10.【答案】A
【解析】解:由题意得,,
,
故选:A.
根据题意求出,根据直角三角形的性质解答即可.
本题考查的是解直角三角形的应用方向角问题,掌握方向角的概念、熟记锐角三角函数的定义是解题的关键.
11.【答案】B
【解析】解:在中,
,,
,
,
,
即河宽米,
故选:B.
在直角三角形PQT中,利用PQ的长,以及的度数,进而得到的度数,根据三角函数即可求得PT的长.
此题考查了解直角三角形的应用方向角问题,掌握方向角与正切函数的定义是解题的关键.
12.【答案】B
【解析】解:如图,延长AB交ED的延长线于G,作于H,于F.
在中,米,CH::,
米,米,
在中,米,BF::,
米,
四边形CFGH是矩形,
米,米,
米,米,
,
,
米,
故选:B.
如图,延长AB交ED的延长线于G,作于H,于想办法求出DG,BG,根据,构建方程解决问题即可.
本题考查解直角三角形的应用,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
13.【答案】
【解析】解:,,
,
.
故答案为.
根据,即可求解.
本题考查了锐角三角函数值的增减性:当角度在间变化时,
正弦值随着角度的增大或减小而增大或减小;
余弦值随着角度的增大或减小而减小或增大;
正切值随着角度的增大或减小而增大或减小.
也考查了不等式的传递性.
14.【答案】
【解析】解:,
故答案为:.
根据二次根式的乘法运算的法则和特殊角的三角函数值计算即可.
本题考查了二次根式的混合运算,特殊角的三角函数值,熟记法则是解题的关键.
15.【答案】
【解析】解:,
故答案为:
利用计算器依次计算可得.
本题主要考查计算器的使用,熟练掌握计算器中乘方和三角函数的按键使用是解题的关键.
16.【答案】1或5
【解析】解:如图1,若为锐角三角形,
,
,
,
设,则,
,
,
解得:或舍,
,,
;
如图2,若为钝角三角形,
由知,,,
,
故答案为:1或5.
分为锐角三角形和钝角三角形两种情况,在中由,可设设,则,结合BD的长根据勾股定理可得,求得x的值后即可得,,在锐角三角形中,在钝角三角形中即可得答案.
本题考查了等腰三角形的性质,解直角三角形,勾股定理的应用,解此题的关键是根据三角形的形状分类讨论.
17.【答案】
【解析】解:根据题意得:海里,,,
在直角三角形APC中,,,
海里,
在直角三角形BPC中,,,
海里,
海里;
故答案为:.
根据题意得:海里,,,在直角三角形APC中,由勾股定理得出海里,在直角三角形BPC中,得出海里,即可得出答案.
本题考查了解直角三角形的应用、勾股定理的应用;求出AC和BC的长度是解决问题的关键.
18.【答案】
【解析】解:在直角中,,,
米;
同理,直角中,米,
则米.
故答案是:.
在直角中利用三角函数求得AD,然后在直角中,利用三角函数求得BD,根据即可求解.
本题考查运用俯角的定义,三角函数,转化为解直角三角形的问题.
19.【答案】解:由已知得,
在中,
,
,
答:眼睛E与显示屏顶端A的水平距离AE约为53km;
如图,过点B作于点F,
,,
,
在中,
,
,
,
,
,
.
答:显示屏顶端A与底座C的距离AC约为34cm.
【解析】由已知得,根据锐角三角函数即可求出眼睛E与显示屏顶端A的水平距离AE;
如图,过点B作于点F,根据锐角三角函数求出AF和BF的长,进而求出显示屏顶端A与底座C的距离AC.
本题考查了解直角三角形的应用仰角俯角问题,解决本题的关键是掌握仰角俯角定义.
20.【答案】解:原式
;
,
由得,,
由得,,
所以,不等式组的解集是.
【解析】本题涉及指数幂、零指数幂、平方根、绝对值、特殊角的三角函数5个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
先求出两个不等式的解集,再求其公共解.
本题主要考查了一元一次不等式组解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到无解;也考查了实数的运算.
21.【答案】解:如图,
过点C作于点F,
可得四边形FBDC是矩形,
,
,
根据题意,得
,
,
根据入射角等于反射角可知:
,
,
,
,
,
解得,
米.
答:旗杆AB的高度为米.
【解析】过点C作于点F,可得四边形FBDC是矩形,根据入射角等于反射角可得,,所以,进而可求AF的长,最后求出AB的长.
本题考查了解直角三角形的应用仰角俯角问题,解决本题的关键是掌握仰角俯角定义.
22.【答案】证明:四边形ABCD是菱形
,,
,
,
,
,
四边形ACED是平行四边形.
解:四边形ACED是平行四边形,
,
,
,
,
,
,
,,,
,
,
.
【解析】想办法证明,即可;
只要证明,再想办法求出即可;
本题考查菱形的性质、平行四边形的判定和性质、解直角三角形、锐角三角函数等知识,解题的关键是熟练掌握平行四边形的判定,学会用转化的思想思考问题.
23.【答案】解:,;
根据已知,把放到正方形网格中,连结GM,
如图4,
可得,,
,,,
,,,
,
∽,
,
,
.
【解析】
解:由图得知:,,,,,,
,
∽,
,
;
故答案为:,;
见答案.
【分析】
由图得知:,,,,,,通过三边对应成比例,两三角形相似得到∽,于是得到结论;
根据已知,把放到正方形网格中,连结GM,如图4,由图得知各个相等的长度,于是得到,得到∽,求得,根据三角形外角的性质即可得到结果.
本题考查了相似三角形的判定和性质,三角函数,勾股定理,外角的性质,找准相似三角形是解题的关键.
24.【答案】证明:,
,
,
,,
,
,
,
,
,,
,
,
平分.
解:如图1中,过点D作于T.
平分,,,
,
,,
,
,
.
解:如图2中,连接BE,过点C作交AE的延长线于T.
,,
,
,,
,
,
≌,
,,
,,
,
,
【解析】想办法证明即可解决问题.
如图1中,过点D作于证明,即可解决问题.
如图2中,连接BE,过点C作交AE的延长线于证明≌可得结论.
本题考查解直角三角形,角平分线的性质,等腰直角三角形的判定和性质,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
第2页,共22页
第1页,共22页
一、选择题
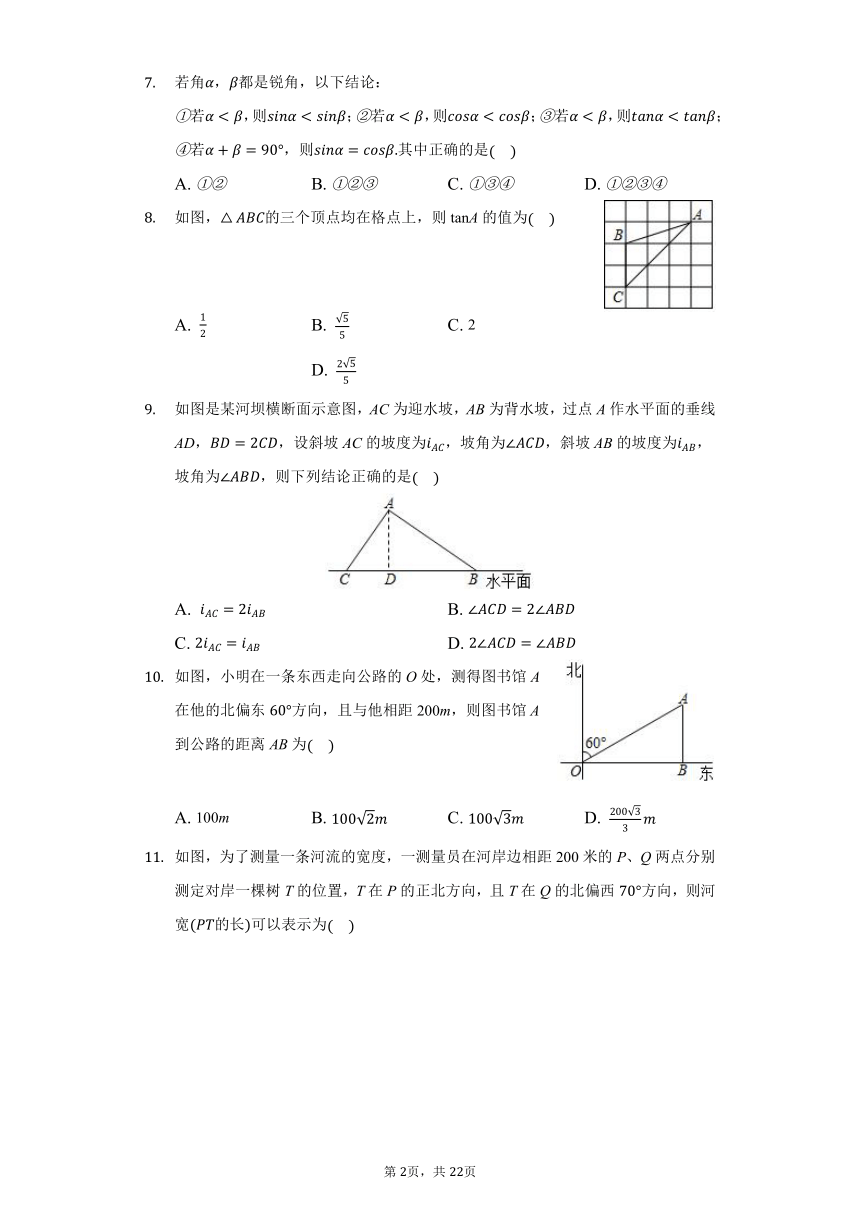
如图,在中,,,若,则BC的长为
A.
8
B.
12
C.
D.
在中,,,则cosA的值等于
A.
B.
C.
或
D.
或
已知为锐角,且,则的度数为
A.
B.
C.
D.
的值是
A.
B.
C.
D.
若计算器的四个键的序号如图所示,在角的度量单位为“度的状态下”用计算器求,正确的按键顺序是。
A.
B.
C.
D.
为了方便行人推车过某天桥,市政府在10m高的天桥一侧修建了40m长的斜道如图所示,我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是
A.
B.
C.
D.
若角,都是锐角,以下结论:
若,则;若,则;若,则;若,则其中正确的是
A.
B.
C.
D.
如图,的三个顶点均在格点上,则tanA的值为
A.
B.
C.
2
D.
如图是某河坝横断面示意图,AC为迎水坡,AB为背水坡,过点A作水平面的垂线AD,,设斜坡AC的坡度为,坡角为,斜坡AB的坡度为,坡角为,则下列结论正确的是
A.
B.
C.
D.
如图,小明在一条东西走向公路的O处,测得图书馆A在他的北偏东方向,且与他相距200m,则图书馆A到公路的距离AB为
A.
100m
B.
C.
D.
如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西方向,则河宽的长可以表示为
A.
米
B.
米
C.
200sin?米
D.
米
中考结束后,小明和好朋友一起前往三亚旅游.他们租住的宾馆AB坐落在坡度为:的斜坡上.宾馆AB高为129米.某天,小明在宾馆顶楼的海景房A处向外看风景,发现宾馆前有一座雕像雕像的高度忽略不计,已知雕像C距离海岸线D的距离CD为260米,与宾馆AB的水平距离为36米,远处海面上一艘即将靠岸的轮船E的俯角为则轮船E距离海岸线D的距离ED的长为米
参考数据:,
A.
262
B.
212
C.
244
D.
276
二、填空题
比较大小:______填“”、“”或“”.
计算:______.
用科学计算器计算:______
结果精确到
在中,,若于D,若,,则CD为______.
一艘货轮由西向东航行,在A处测得灯塔P在它的北偏东方向,继续航行到达B处,测得灯塔P在正南方向10海里的C处是港口,点A、B、C在一条直线上,则这艘货轮由A处到B处航行的路程为______海里结果保留根号.
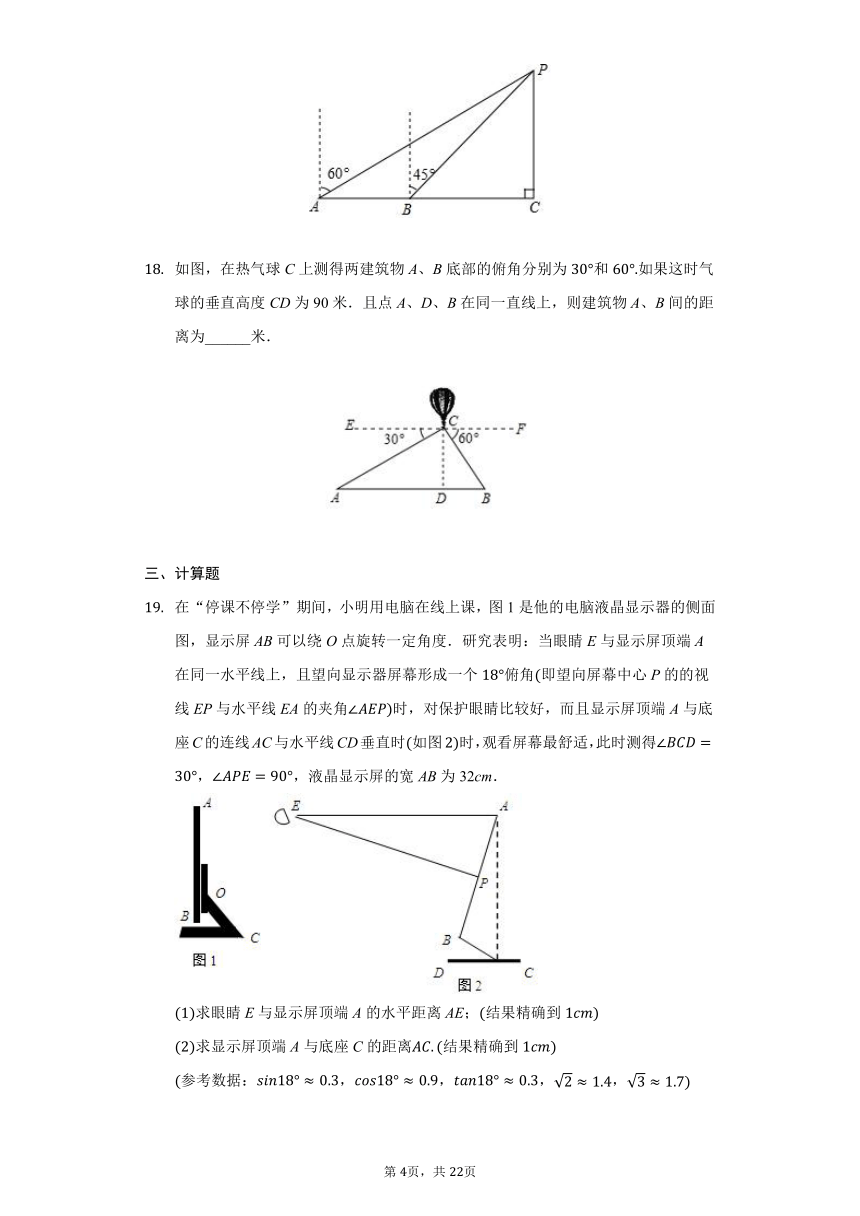
如图,在热气球C上测得两建筑物A、B底部的俯角分别为和如果这时气球的垂直高度CD为90米.且点A、D、B在同一直线上,则建筑物A、B间的距离为______米.
三、计算题
在“停课不停学”期间,小明用电脑在线上课,图1是他的电脑液晶显示器的侧面图,显示屏AB可以绕O点旋转一定角度.研究表明:当眼睛E与显示屏顶端A在同一水平线上,且望向显示器屏幕形成一个俯角即望向屏幕中心P的的视线EP与水平线EA的夹角时,对保护眼睛比较好,而且显示屏顶端A与底座C的连线AC与水平线CD垂直时如图时,观看屏幕最舒适,此时测得,,液晶显示屏的宽AB为32cm.
求眼睛E与显示屏顶端A的水平距离AE;结果精确到
求显示屏顶端A与底座C的距离结果精确到
参考数据:,,,,
计算;
解不等式组.
小明和小华进行社会实践活动时,想利用所学的知识测量某旗杆AB的高度.小明站在点D处利用测倾器测得旗杄顶端A的仰角为,小华在BD之间放置一个镜子,并调整镜子的位置,当镜子恰好放在点E处时,位于点D处的小明正好在镜子中看到旗杆顶端A,此时DE的距离为米,已知测倾器的高为米.请你根据以上信息,计算旗杆AB的高度.
四、解答题
如图,在菱形ABCD中,对角线AC与BD相交于点O,过点D作交BC的延长线于点E.
求证:四边形ACED是平行四边形;
若,,求的值.
阅读下列材料:小华遇到这样一个问题:已知:如图1,在中,三边的长分别为,,,求的正切值.
小华是这样解决问题的:如图2所示,先在一个正方形网格每个小正方形的边长均为中画出格点三个顶点都在小正方形的顶点处,然后在这个正方形网格中再画一个和相似的格点,从而使问题得解.
图2中与相等的角为______,的正切值为______;
参考小华解决问题的方法,利用图4中的正方形网格每个小正方形的边长均为
解决问题:如图3,在中,,,,延长HK,求的度数.
已知,,,D是AB边上一点,连接CD,E是CD上一点,且.
如图1,若,
求证:CD平分;
求的值;
如图2,连接BE,若,求的值.
答案和解析
1.【答案】C
【解析】解:法一、在中,
,
.
.
故选:C.
法二、在中,
,
.
,
.
故选:C.
根据锐角三角函数的边角间关系,先求出AB,再利用勾股定理求出BC.
本题考查了解直角三角形.掌握直角三角形的边角间关系是解决本题的关键.
2.【答案】C
【解析】解:当为直角三角形时,存在两种情况:
当AB为斜边,,
,,
.
;
当AC为斜边,,
由勾股定理得:,
;
综上所述,cosA的值等于或.
故选:C.
因为原题没有说明哪个角是直角,所以要分情况讨论:为斜边,为斜边,根据勾股定理求得AB的值,然后根据余弦的定义即可求解.
本题考查了余弦函数的定义,理解定义是关键,并注意分类讨论.
3.【答案】C
【解析】解:为锐角,,,
.
故选:C.
根据解答即可.
此题比较简单,只要熟知特殊角度的三角函数值即可.
4.【答案】B
【解析】解:,
故选:B.
根据特殊角的三角函数值可得答案.
此题主要考查了特殊角的三角函数值,关键是掌握、、角的各种三角函数值.
5.【答案】B
【解析】
【分析】
本题考查用计算器求锐角三角函数,属于常识题,了解三角函数的计算即可求出答案.
【解答】
解:根据计算器的计算常识可知,
求的步骤为.
故选B.
6.【答案】A
【解析】解:,
所以用科学计算器求这条斜道倾斜角的度数时,按键顺序为:
故选A.
先利用正弦的定义得到,然后利用计算器求锐角.
本题考查了计算器三角函数:正确使用计算器,一般情况下,三角函数值直接可以求出,已知三角函数值求角需要用第二功能键.
7.【答案】C
【解析】解:随的增大而增大,若,则,此结论正确;
随的增大而减小,若,则,此结论错误;
随的增大而增大,若,则,此结论正确;
若,则,此结论正确;
综上,正确的结论为,
故选:C.
根据锐角范围内、、的增减性及互余两锐角的正余弦函数间的关系可得.
本题主要考查互余两锐角三角函数关系,解题的关键是掌握锐角范围内、、的增减性及互余两锐角的正余弦函数间的关系.
8.【答案】A
【解析】
【分析】
此题主要考查了解直角三角形,正确构造直角三角形是解题关键.
直接利用网格结合锐角三角函数关系得出,进而得出答案.
【解答】
解:如图所示:连接BD,
由网格可得,
则.
故选:A.
9.【答案】A
【解析】解:斜坡AC的坡度,斜坡AB的坡度,
,
,A正确,C错误;
,B错误;
,D错误;
故选:A.
根据坡度的概念分别表示出、,根据题意判断即可.
本题考查的是坡度坡角的概念,掌握坡度是坡面的铅直高度h和水平宽度l的比是解题的关键.
10.【答案】A
【解析】解:由题意得,,
,
故选:A.
根据题意求出,根据直角三角形的性质解答即可.
本题考查的是解直角三角形的应用方向角问题,掌握方向角的概念、熟记锐角三角函数的定义是解题的关键.
11.【答案】B
【解析】解:在中,
,,
,
,
,
即河宽米,
故选:B.
在直角三角形PQT中,利用PQ的长,以及的度数,进而得到的度数,根据三角函数即可求得PT的长.
此题考查了解直角三角形的应用方向角问题,掌握方向角与正切函数的定义是解题的关键.
12.【答案】B
【解析】解:如图,延长AB交ED的延长线于G,作于H,于F.
在中,米,CH::,
米,米,
在中,米,BF::,
米,
四边形CFGH是矩形,
米,米,
米,米,
,
,
米,
故选:B.
如图,延长AB交ED的延长线于G,作于H,于想办法求出DG,BG,根据,构建方程解决问题即可.
本题考查解直角三角形的应用,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
13.【答案】
【解析】解:,,
,
.
故答案为.
根据,即可求解.
本题考查了锐角三角函数值的增减性:当角度在间变化时,
正弦值随着角度的增大或减小而增大或减小;
余弦值随着角度的增大或减小而减小或增大;
正切值随着角度的增大或减小而增大或减小.
也考查了不等式的传递性.
14.【答案】
【解析】解:,
故答案为:.
根据二次根式的乘法运算的法则和特殊角的三角函数值计算即可.
本题考查了二次根式的混合运算,特殊角的三角函数值,熟记法则是解题的关键.
15.【答案】
【解析】解:,
故答案为:
利用计算器依次计算可得.
本题主要考查计算器的使用,熟练掌握计算器中乘方和三角函数的按键使用是解题的关键.
16.【答案】1或5
【解析】解:如图1,若为锐角三角形,
,
,
,
设,则,
,
,
解得:或舍,
,,
;
如图2,若为钝角三角形,
由知,,,
,
故答案为:1或5.
分为锐角三角形和钝角三角形两种情况,在中由,可设设,则,结合BD的长根据勾股定理可得,求得x的值后即可得,,在锐角三角形中,在钝角三角形中即可得答案.
本题考查了等腰三角形的性质,解直角三角形,勾股定理的应用,解此题的关键是根据三角形的形状分类讨论.
17.【答案】
【解析】解:根据题意得:海里,,,
在直角三角形APC中,,,
海里,
在直角三角形BPC中,,,
海里,
海里;
故答案为:.
根据题意得:海里,,,在直角三角形APC中,由勾股定理得出海里,在直角三角形BPC中,得出海里,即可得出答案.
本题考查了解直角三角形的应用、勾股定理的应用;求出AC和BC的长度是解决问题的关键.
18.【答案】
【解析】解:在直角中,,,
米;
同理,直角中,米,
则米.
故答案是:.
在直角中利用三角函数求得AD,然后在直角中,利用三角函数求得BD,根据即可求解.
本题考查运用俯角的定义,三角函数,转化为解直角三角形的问题.
19.【答案】解:由已知得,
在中,
,
,
答:眼睛E与显示屏顶端A的水平距离AE约为53km;
如图,过点B作于点F,
,,
,
在中,
,
,
,
,
,
.
答:显示屏顶端A与底座C的距离AC约为34cm.
【解析】由已知得,根据锐角三角函数即可求出眼睛E与显示屏顶端A的水平距离AE;
如图,过点B作于点F,根据锐角三角函数求出AF和BF的长,进而求出显示屏顶端A与底座C的距离AC.
本题考查了解直角三角形的应用仰角俯角问题,解决本题的关键是掌握仰角俯角定义.
20.【答案】解:原式
;
,
由得,,
由得,,
所以,不等式组的解集是.
【解析】本题涉及指数幂、零指数幂、平方根、绝对值、特殊角的三角函数5个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.
先求出两个不等式的解集,再求其公共解.
本题主要考查了一元一次不等式组解集的求法,其简便求法就是用口诀求解.求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到无解;也考查了实数的运算.
21.【答案】解:如图,
过点C作于点F,
可得四边形FBDC是矩形,
,
,
根据题意,得
,
,
根据入射角等于反射角可知:
,
,
,
,
,
解得,
米.
答:旗杆AB的高度为米.
【解析】过点C作于点F,可得四边形FBDC是矩形,根据入射角等于反射角可得,,所以,进而可求AF的长,最后求出AB的长.
本题考查了解直角三角形的应用仰角俯角问题,解决本题的关键是掌握仰角俯角定义.
22.【答案】证明:四边形ABCD是菱形
,,
,
,
,
,
四边形ACED是平行四边形.
解:四边形ACED是平行四边形,
,
,
,
,
,
,
,,,
,
,
.
【解析】想办法证明,即可;
只要证明,再想办法求出即可;
本题考查菱形的性质、平行四边形的判定和性质、解直角三角形、锐角三角函数等知识,解题的关键是熟练掌握平行四边形的判定,学会用转化的思想思考问题.
23.【答案】解:,;
根据已知,把放到正方形网格中,连结GM,
如图4,
可得,,
,,,
,,,
,
∽,
,
,
.
【解析】
解:由图得知:,,,,,,
,
∽,
,
;
故答案为:,;
见答案.
【分析】
由图得知:,,,,,,通过三边对应成比例,两三角形相似得到∽,于是得到结论;
根据已知,把放到正方形网格中,连结GM,如图4,由图得知各个相等的长度,于是得到,得到∽,求得,根据三角形外角的性质即可得到结果.
本题考查了相似三角形的判定和性质,三角函数,勾股定理,外角的性质,找准相似三角形是解题的关键.
24.【答案】证明:,
,
,
,,
,
,
,
,
,,
,
,
平分.
解:如图1中,过点D作于T.
平分,,,
,
,,
,
,
.
解:如图2中,连接BE,过点C作交AE的延长线于T.
,,
,
,,
,
,
≌,
,,
,,
,
,
【解析】想办法证明即可解决问题.
如图1中,过点D作于证明,即可解决问题.
如图2中,连接BE,过点C作交AE的延长线于证明≌可得结论.
本题考查解直角三角形,角平分线的性质,等腰直角三角形的判定和性质,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.
第2页,共22页
第1页,共22页
