人教版八年级上册13.3.1等腰三角形课件(21张)
文档属性
| 名称 | 人教版八年级上册13.3.1等腰三角形课件(21张) |  | |
| 格式 | zip | ||
| 文件大小 | 410.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-19 23:13:52 | ||
图片预览




文档简介
(共21张PPT)
13.3.1等腰三角形
猜一猜
形状像座山,稳定性能强.
三竿首尾连,两竿一样长.
学问不简单.
(打一数学图形--
)
等腰三角形
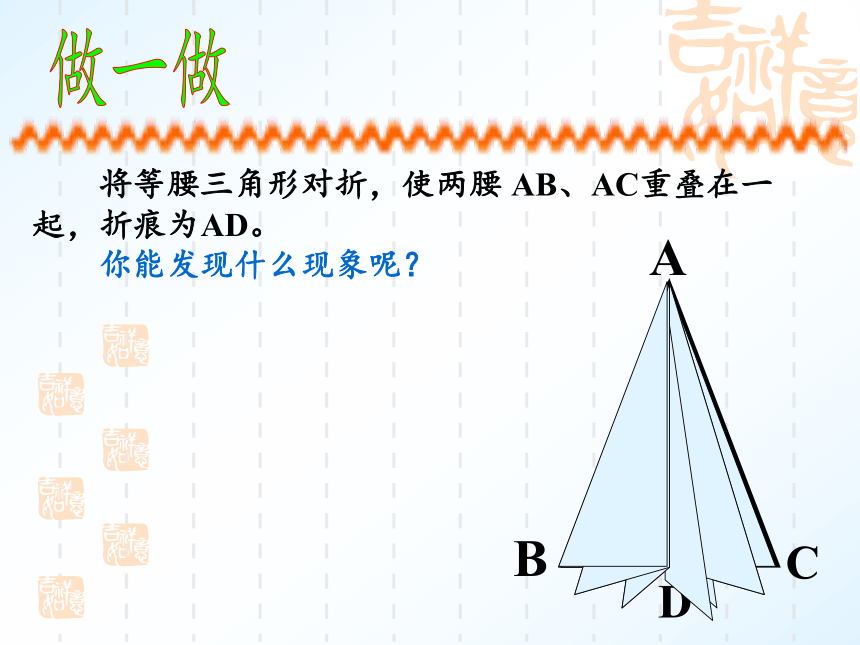
做一做
将等腰三角形对折,使两腰
AB、AC重叠在一起,折痕为AD。
你能发现什么现象呢?
D
A
B
C
探究一:探索等腰三角形的性质
重点知识★
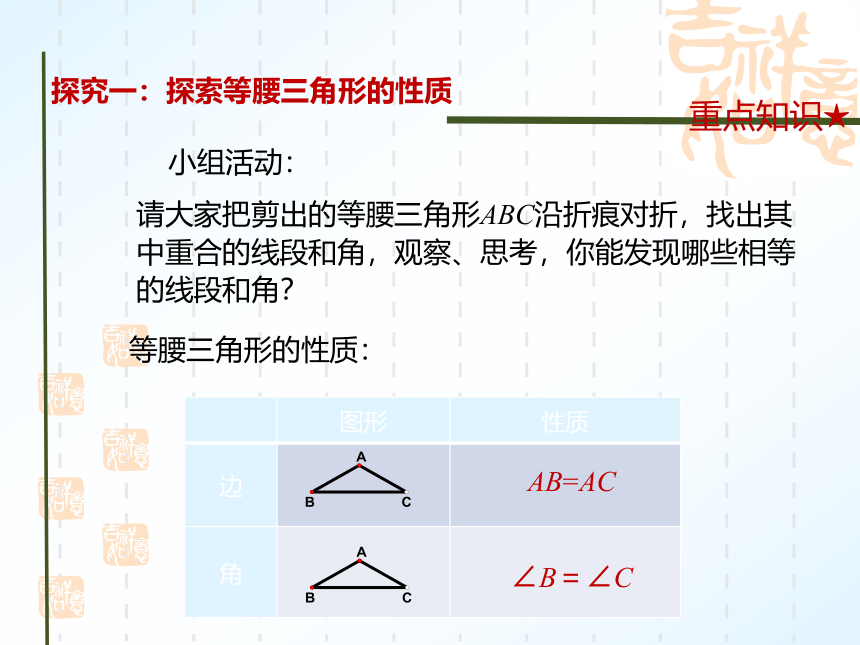
小组活动:
请大家把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角,观察、思考,你能发现哪些相等的线段和角?
等腰三角形的性质:
?
图形
性质
边
?
?
角
?
?
AB=AC
∠B=∠C
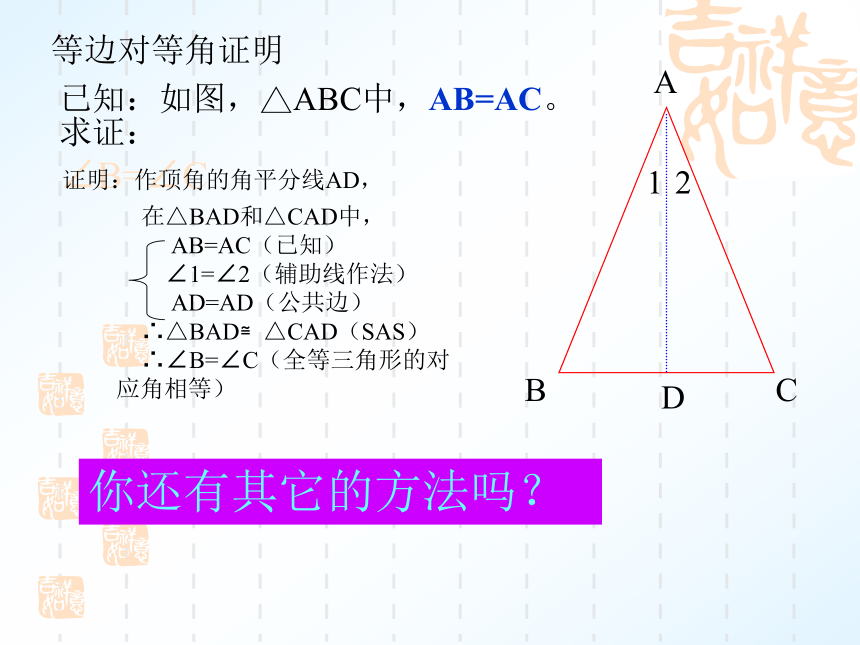
已知:如图,△ABC中,AB=AC。
求证:∠B=∠C
A
B
C
D
1
2
证明:作顶角的角平分线AD,
在△BAD和△CAD中,
AB=AC(已知)
∠1=∠2(辅助线作法)
AD=AD(公共边)
∴△BAD≌△CAD(SAS)
∴∠B=∠C(全等三角形的对应角相等)
你还有其它的方法吗?
等边对等角证明
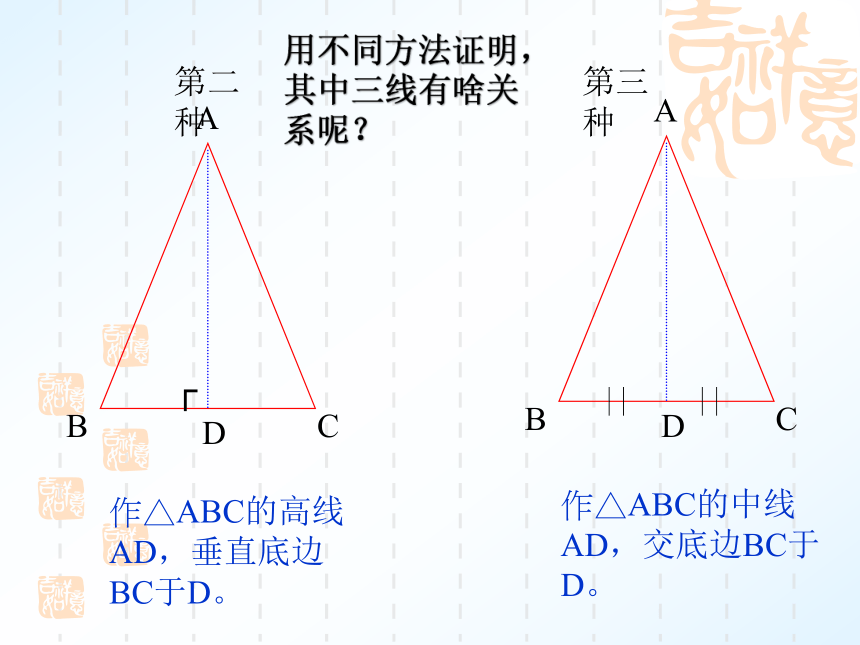
第二种
第三种
A
B
C
D
A
B
C
D
┌
作△ABC的高线AD,垂直底边BC于D。
作△ABC的中线AD,交底边BC于D。
用不同方法证明,其中三线有啥关系呢?
等腰三角形是轴对称图形
∠B=∠C
等腰三角形两个底角相等
简写成“等边对等角”
BD=CD,AD为底边上的中线
∠ADB=∠ADC,AD为底边上的高线
∠BAD=∠CAD,AD为顶角平分线
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。
简称“三线合一”
“等边对等角”必须在同一个等腰三角形中才成立。
“三线合一”是对等腰三角形的顶角平分线、底边上的中线和高而言的。
要注意哦!
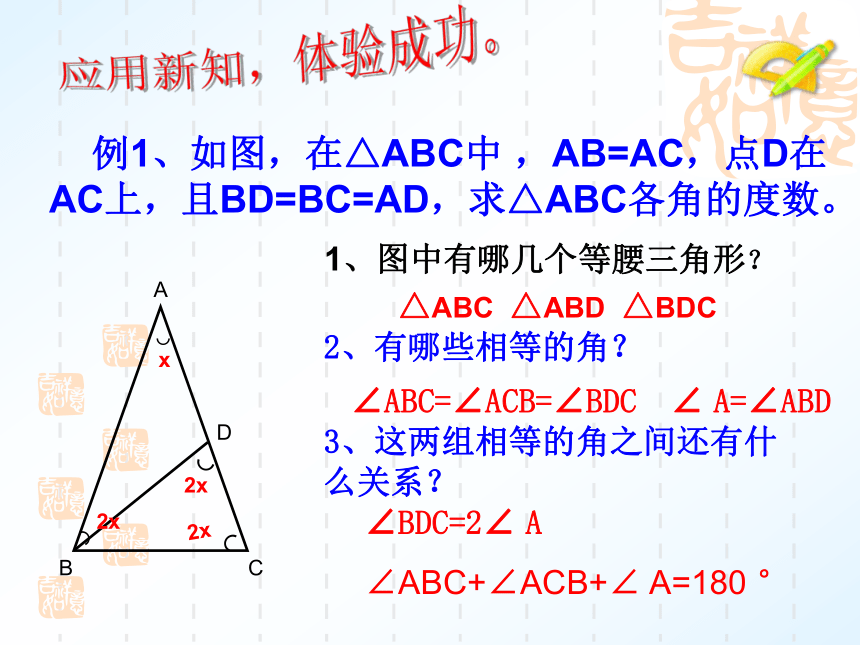
例1、如图,在△ABC中
,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。
1、图中有哪几个等腰三角形?
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
应用新知,体验成功。
△ABC
△ABD
△BDC
2、有哪些相等的角?
∠ABC=∠ACB=∠BDC
∠
A=∠ABD
3、这两组相等的角之间还有什么关系?
∠BDC=2∠
A
∠ABC+∠ACB+∠
A=180
°
例1、如图,在△ABC中
,AB=AC,点D在AC上,且
BD=BC=AD,求△ABC各角的度数。
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD
(等边对等角)
设∠A=x,则∠BDC=
∠A+
∠ABD=2x,
从而∠ABC=
∠C=
∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中,
∠A=36°,∠ABC=∠C=72°
x
⌒
2x
⌒
2x
⌒
⌒
2x
练习1
在三角形ABC中,已知AB=AC,且∠B=80°
,则∠C=
___度,∠A=____度?
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
∵∠B=80°
(已知)
∴∠C=80°
又∵∠A+∠B+∠C=180°
(三角形内角和为180°
)
∴∠A=180°-
∠B-∠C
∠A=20°
B
C
A
2在三角形ABC中,已知AB=AC,且∠
A=50°
,则∠B=——度,∠C=——度?
C
B
A
∵AB=AC(已知)
∴∠B=∠C(等边对等角)又∵∠A+∠B+∠C=180°
(三角形内角和为180°
)
∠A=50°
(已知)
∴∠B=65°
∠C=65°
性质1:等边对等角
性质2:“三线合一”
等
腰
三
角
形
1、等腰三角形的两个底角相等(等边对等角)
2、等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
小结
例2、已知:如图,点D、E在△ABC的边BC上,AB=AC,AD=AE.求证:BD=CE
.
过A
作AF⊥BC于F,
∵
AB=AC
,
∴BF=CF
,
证明:
B
A
E
C
D
同理
∵
AD=AE
,
∴DF=EF
,
∴BF–DF=CF–EF
,
即
BD=CE
F
应用新知,体验成功。
练习
1.判断对错
(1)等腰三角形的角平分线、中线和高互相重合。(
)
(2)有一个角是60°的等腰三角形,其它两个
内角也为60°.
(
)
(3)等腰三角形的底角都是锐角.
(
)
(4)钝角三角形不可能是等腰三角形
.
(
)
×
×
3.等腰三角形一腰上的高与另一腰的夹角为60°,则这个等腰三角形的顶角为(
)
A.30°
B.150°
C.30°或150°
D.120°
1.△ABC中,AB=AC,∠A=70°,则∠B=______
2.等腰三角形一底角的外角为105°,那么它的顶角为______度
C
55°
30
2.填空选择
3.
在三角形ABC中,AB=AC,且AD
⊥BC,已知BD=2cm,求DC=___cm,
BC=___cm?
C
B
D
A
1
2
∵
AB=AC
,AD
⊥BC(已知)
∴BD=CD(等腰三角形的高与底边上的中线重合)
即(等腰三角形三线合一)
∵BD=2cm(已知)
∴CD=2cm
4.已知AD⊥
BC,试找出等腰三角形ABC
(AB=AC)中,存在相等关系的量。
C
B
D
A
1
2
∠B=∠C
∠1=∠2
∠BDA=∠CDA=90°
BD=CD
4.
根据等腰三角形的性质,在△ABC中,
AB=AC时,
(1)
∵AD⊥BC,∴∠_____
=
∠_____,____=
____.
(2)
∵AD是中线,∴____⊥____
,∠_____
=∠_____.
(3)
∵AD是角平分线,∴____
⊥____
,_____
=_____.
A
B
C
D
BAD
CAD
CAD
BD
CD
AD
BC
BD
BAD
BC
AD
CD
测试
小结
本节课你学到了什么?
等腰三角形的性质及性质应用
文字叙述
几何语言
等腰三角形的两底角相等(简称等边对等角)
∵AB=AC
∴∠B=∠C
等腰三角形顶角的平分线平分底边并且垂直于底边(简称三线合一)
∵AB=AC,∠1=∠2
∴AD⊥BC,BD=CD
再见
谢谢!
13.3.1等腰三角形
猜一猜
形状像座山,稳定性能强.
三竿首尾连,两竿一样长.
学问不简单.
(打一数学图形--
)
等腰三角形
做一做
将等腰三角形对折,使两腰
AB、AC重叠在一起,折痕为AD。
你能发现什么现象呢?
D
A
B
C
探究一:探索等腰三角形的性质
重点知识★
小组活动:
请大家把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角,观察、思考,你能发现哪些相等的线段和角?
等腰三角形的性质:
?
图形
性质
边
?
?
角
?
?
AB=AC
∠B=∠C
已知:如图,△ABC中,AB=AC。
求证:∠B=∠C
A
B
C
D
1
2
证明:作顶角的角平分线AD,
在△BAD和△CAD中,
AB=AC(已知)
∠1=∠2(辅助线作法)
AD=AD(公共边)
∴△BAD≌△CAD(SAS)
∴∠B=∠C(全等三角形的对应角相等)
你还有其它的方法吗?
等边对等角证明
第二种
第三种
A
B
C
D
A
B
C
D
┌
作△ABC的高线AD,垂直底边BC于D。
作△ABC的中线AD,交底边BC于D。
用不同方法证明,其中三线有啥关系呢?
等腰三角形是轴对称图形
∠B=∠C
等腰三角形两个底角相等
简写成“等边对等角”
BD=CD,AD为底边上的中线
∠ADB=∠ADC,AD为底边上的高线
∠BAD=∠CAD,AD为顶角平分线
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。
简称“三线合一”
“等边对等角”必须在同一个等腰三角形中才成立。
“三线合一”是对等腰三角形的顶角平分线、底边上的中线和高而言的。
要注意哦!
例1、如图,在△ABC中
,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。
1、图中有哪几个等腰三角形?
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
应用新知,体验成功。
△ABC
△ABD
△BDC
2、有哪些相等的角?
∠ABC=∠ACB=∠BDC
∠
A=∠ABD
3、这两组相等的角之间还有什么关系?
∠BDC=2∠
A
∠ABC+∠ACB+∠
A=180
°
例1、如图,在△ABC中
,AB=AC,点D在AC上,且
BD=BC=AD,求△ABC各角的度数。
A
B
C
D
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC,∠A=∠ABD
(等边对等角)
设∠A=x,则∠BDC=
∠A+
∠ABD=2x,
从而∠ABC=
∠C=
∠BDC=2x,
于是在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180°,
解得x=36°,
在△ABC中,
∠A=36°,∠ABC=∠C=72°
x
⌒
2x
⌒
2x
⌒
⌒
2x
练习1
在三角形ABC中,已知AB=AC,且∠B=80°
,则∠C=
___度,∠A=____度?
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
∵∠B=80°
(已知)
∴∠C=80°
又∵∠A+∠B+∠C=180°
(三角形内角和为180°
)
∴∠A=180°-
∠B-∠C
∠A=20°
B
C
A
2在三角形ABC中,已知AB=AC,且∠
A=50°
,则∠B=——度,∠C=——度?
C
B
A
∵AB=AC(已知)
∴∠B=∠C(等边对等角)又∵∠A+∠B+∠C=180°
(三角形内角和为180°
)
∠A=50°
(已知)
∴∠B=65°
∠C=65°
性质1:等边对等角
性质2:“三线合一”
等
腰
三
角
形
1、等腰三角形的两个底角相等(等边对等角)
2、等腰三角形顶角的平分线,底边上的中线和底边上的高互相重合(等腰三角形三线合一)
小结
例2、已知:如图,点D、E在△ABC的边BC上,AB=AC,AD=AE.求证:BD=CE
.
过A
作AF⊥BC于F,
∵
AB=AC
,
∴BF=CF
,
证明:
B
A
E
C
D
同理
∵
AD=AE
,
∴DF=EF
,
∴BF–DF=CF–EF
,
即
BD=CE
F
应用新知,体验成功。
练习
1.判断对错
(1)等腰三角形的角平分线、中线和高互相重合。(
)
(2)有一个角是60°的等腰三角形,其它两个
内角也为60°.
(
)
(3)等腰三角形的底角都是锐角.
(
)
(4)钝角三角形不可能是等腰三角形
.
(
)
×
×
3.等腰三角形一腰上的高与另一腰的夹角为60°,则这个等腰三角形的顶角为(
)
A.30°
B.150°
C.30°或150°
D.120°
1.△ABC中,AB=AC,∠A=70°,则∠B=______
2.等腰三角形一底角的外角为105°,那么它的顶角为______度
C
55°
30
2.填空选择
3.
在三角形ABC中,AB=AC,且AD
⊥BC,已知BD=2cm,求DC=___cm,
BC=___cm?
C
B
D
A
1
2
∵
AB=AC
,AD
⊥BC(已知)
∴BD=CD(等腰三角形的高与底边上的中线重合)
即(等腰三角形三线合一)
∵BD=2cm(已知)
∴CD=2cm
4.已知AD⊥
BC,试找出等腰三角形ABC
(AB=AC)中,存在相等关系的量。
C
B
D
A
1
2
∠B=∠C
∠1=∠2
∠BDA=∠CDA=90°
BD=CD
4.
根据等腰三角形的性质,在△ABC中,
AB=AC时,
(1)
∵AD⊥BC,∴∠_____
=
∠_____,____=
____.
(2)
∵AD是中线,∴____⊥____
,∠_____
=∠_____.
(3)
∵AD是角平分线,∴____
⊥____
,_____
=_____.
A
B
C
D
BAD
CAD
CAD
BD
CD
AD
BC
BD
BAD
BC
AD
CD
测试
小结
本节课你学到了什么?
等腰三角形的性质及性质应用
文字叙述
几何语言
等腰三角形的两底角相等(简称等边对等角)
∵AB=AC
∴∠B=∠C
等腰三角形顶角的平分线平分底边并且垂直于底边(简称三线合一)
∵AB=AC,∠1=∠2
∴AD⊥BC,BD=CD
再见
谢谢!
