人教版(2019)物理 选择性必修第一册 4.4 实验:用双缝干涉测量光的波长 课后作业(含解析)
文档属性
| 名称 | 人教版(2019)物理 选择性必修第一册 4.4 实验:用双缝干涉测量光的波长 课后作业(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 215.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-19 18:09:58 | ||
图片预览

文档简介
新人教版选择性必修一课后作业第四章光 实验:用双缝干涉测量光的波长
一、选择题
1.用单色光做双缝干涉实验,下列说法正确的是( )
A.相邻两亮条纹或暗条纹的中心间距相等
B.中央亮条纹的宽度是两侧亮条纹宽度的2倍
C.屏与双缝之间的距离减小,则屏上条纹间的距离增大
D.在实验装置不变的情况下,红光的条纹间距小于蓝光的条纹间距
2.用如图所示的装置来观察光的双缝干涉现象时,以下推断正确的是( )
A.狭缝屏的作用是使入射光到达双缝屏时,双缝就成了两个振动情况总是相同的光源
B.若入射光是白光,则像屏上的条纹是黑白相间的干涉条纹
C.屏上某点到双缝的距离差为入射光波长的1.5倍时,该点处一定是亮条纹
D.双缝干涉中亮条纹之间的距离相等,暗条纹之间的距离不相等
3.(多选)在“用双缝干涉测量光的波长”实验中(实验装置如图),下列说法哪些是正确的( )
A.调节光源高度,使光束沿遮光筒轴线照在屏中心时,应放上单缝和双缝
B.测量某条干涉亮条纹位置时,应使分划板中心刻线与该亮条纹的中心对齐
C.为了减小测量误差,可测出n条亮条纹间的距离a,求出相邻两条亮条纹间距Δx=an-1
D.某同学用黄光作为入射光,为了增大干涉条纹的间距,可以采用的方法是改用蓝光作为入射光
4.某次实验中,测得第一级亮条纹和第三级亮条纹中心相距4.0×10-2 m,若双缝间距为0.1 mm,双缝到屏的距离为l=4.0 m,则光波的波长为( )
A.8.0×10-8 m B.5.0×10-7 m
C.1.5×10-8 m D.1.0×10-7 m
5.在“用双缝干涉测量光的波长”的实验中,调节测量头的位置,使分划板中心刻线对齐某亮条纹的中心,如图所示,此时手轮的读数是 mm。转动测量头,使分划板中心刻线向一侧移动到另一条亮条纹中心位置,再次记下手轮上的读数。若实验测得的4条亮条纹中心间的距离为0.960 mm,且已知双缝间距d=1.5 mm,双缝到屏的距离l=100 cm,则对应的光波的波长为λ= cm。?
在用双缝干涉测光的波长的实验中,请按照题目要求回答下列问题。
(1)甲、乙两图都是光的条纹形状示意图,其中干涉图样是 。?
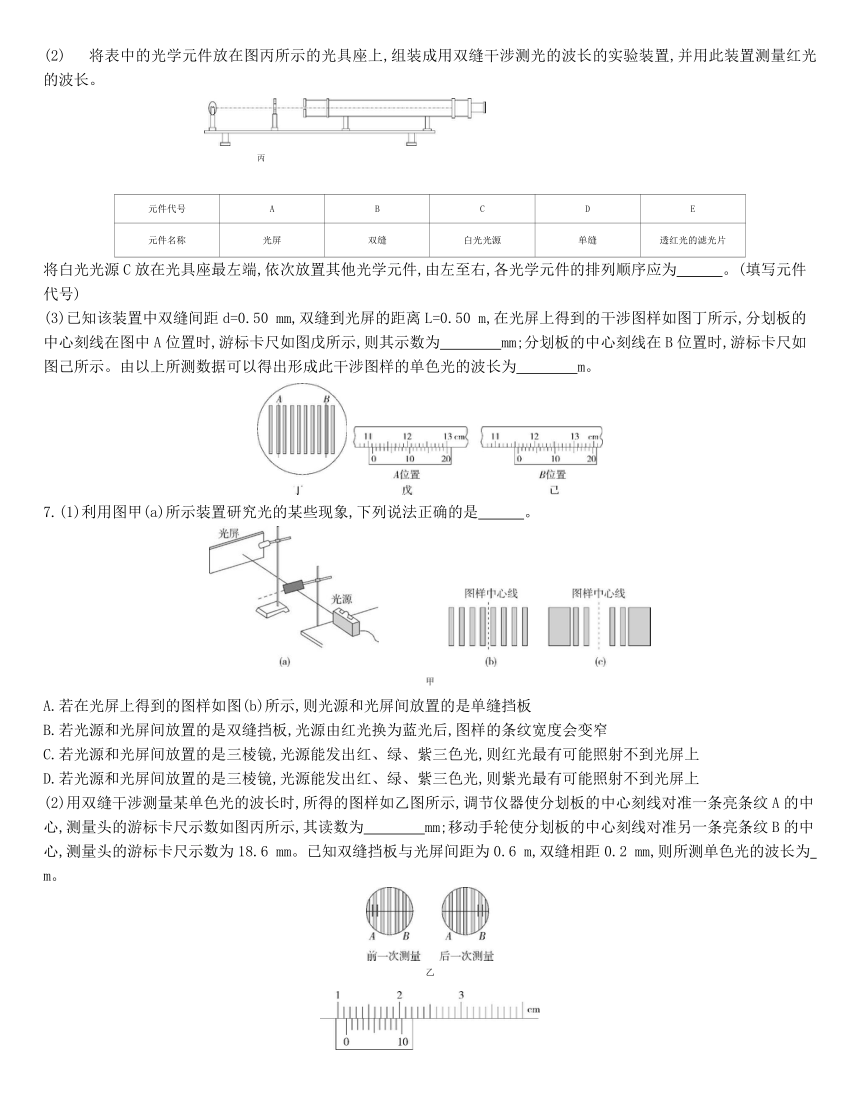
将表中的光学元件放在图丙所示的光具座上,组装成用双缝干涉测光的波长的实验装置,并用此装置测量红光的波长。
161099567310 丙
元件代号
A
B
C
D
E
元件名称
光屏
双缝
白光光源
单缝
透红光的滤光片
将白光光源C放在光具座最左端,依次放置其他光学元件,由左至右,各光学元件的排列顺序应为 。(填写元件代号)?
(3)已知该装置中双缝间距d=0.50 mm,双缝到光屏的距离L=0.50 m,在光屏上得到的干涉图样如图丁所示,分划板的中心刻线在图中A位置时,游标卡尺如图戊所示,则其示数为 mm;分划板的中心刻线在B位置时,游标卡尺如图己所示。由以上所测数据可以得出形成此干涉图样的单色光的波长为 m。?
7.(1)利用图甲(a)所示装置研究光的某些现象,下列说法正确的是 。?
甲
A.若在光屏上得到的图样如图(b)所示,则光源和光屏间放置的是单缝挡板
B.若光源和光屏间放置的是双缝挡板,光源由红光换为蓝光后,图样的条纹宽度会变窄
C.若光源和光屏间放置的是三棱镜,光源能发出红、绿、紫三色光,则红光最有可能照射不到光屏上
D.若光源和光屏间放置的是三棱镜,光源能发出红、绿、紫三色光,则紫光最有可能照射不到光屏上
(2)用双缝干涉测量某单色光的波长时,所得的图样如乙图所示,调节仪器使分划板的中心刻线对准一条亮条纹A的中心,测量头的游标卡尺示数如图丙所示,其读数为 mm;移动手轮使分划板的中心刻线对准另一条亮条纹B的中心,测量头的游标卡尺示数为18.6 mm。已知双缝挡板与光屏间距为0.6 m,双缝相距0.2 mm,则所测单色光的波长为 m。?
乙
丙
8.某同学在实验室找到了一台陈旧的激光器,铭牌已模糊不清,为了测出该激光器发出光的波长,他在实验室中进行了以下操作:
a.将双缝放置在距墙面恰好是5块完整地板砖的位置;
b.用激光器照射双缝,在墙面上得到了如图所示的清晰的干涉条纹。
(1)图中第五条亮条纹中心位置的读数为 cm,相邻两条亮条纹间距Δx= cm;?
(2)已知所用双缝的宽度d=0.10 mm,实验室的地面由“80 cm×80 cm”的地板砖铺成,则该激光器发出光的波长为 m(结果保留2位有效数字)。?
9.洛埃德(H.Lloyd)在1834年提出了一种更简单的观察光的干涉现象的装置——洛埃德镜。如图所示,从单缝S发出的光,一部分入射到平面镜后反射到光屏上,另一部分直接投射到光屏上,在光屏上两光束交叠区域里将出现干涉条纹。单缝S通过平面镜成的像是S'。
(1)通过洛埃德镜在屏上可以观察到明暗相间的干涉条纹,这和双缝干涉实验得到的干涉条纹一致。如果S被视为其中的一个缝, 相当于另一个“缝”。?
(2)实验表明,光从光疏介质射向光密介质界面发生反射时,在入射角接近90°时,反射光与入射光相比,相位有π的变化,即半波损失。如果把光屏移动到和平面镜接触,接触点P处是 (填“亮条纹”或“暗条纹”)。?
(3)实验中,已知单缝S到平面镜的距离为h=0.15 mm,单缝到光屏的距离为D=1.2 m,观测到第3条亮条纹到第12条亮条纹的中心间距为22.78 mm,则该单色光的波长λ= m(结果保留3位有效数字)。?
10.如图所示为“双棱镜干涉”实验装置,S为单色光源。A为一个顶角略小于180°的等腰三角形棱镜,P为光屏,S位于棱镜的对称轴上,光屏与棱镜底边平行。调节光路,可在屏上观察到干涉条纹。这是由于光源S发出的光经棱镜作用后,相当于在没有棱镜时,两个分别位于图中S1和S2位置的相干光源所发出的光的叠加(S1和S2的连线与棱镜底边平行)。已知S1和S2的位置可由其他实验方法确定,类比“双缝干涉测波长”的实验,可以推测出,若要利用“双棱镜干涉”测量光源S发出的单色光的波长,需要测量的物理量是 、 和 。?
答案
一、选择题
1.A 因为相邻两亮条纹或暗条纹的中心间距Δx=ldλ,其中d为双缝间的距离,l为双缝到屏的距离,λ为光波波长,可见相邻两亮条纹或暗条纹之间的距离相等,A正确,B错误。由公式Δx=ldλ可知,l减小,屏上条纹间距减小,C错误。因为λ红>λ蓝,所以Δx红>Δx蓝,D错误。
2.A 狭缝的作用是形成线光源,使得入射光到达双缝屏时,双缝就成了两个振动情况总是相同的光源,故A正确;若入射光是白光,则像屏上产生的条纹是彩色的干涉条纹,故B错误;像屏上某点到双缝的距离差为入射光波长的1.5倍时,该点是振动减弱点,该处一定是暗条纹,故C错误;干涉条纹是等间距的,相邻的两个亮条纹或相邻的两个暗条纹间距相等,故D错误。
3.BC 调节光源高度,使光束沿遮光筒轴线照在屏中心时,不需放单缝和双缝,故A错误。测量某条干涉亮条纹位置时,应使分划板中心刻线与该亮条纹的中心对齐,故B正确。n条亮条纹之间有n-1个间距,相邻两条亮条纹的间距Δx=an-1,故C正确。某同学用黄光作为入射光,根据Δx=ldλ可知,为了增大干涉条纹的间距,应用波长比黄光长的红光或橙光作为入射光,不可以改用波长比黄光短的蓝光作为入射光,故D错误。
4.B 根据公式Δx=ldλ,Δx=4.0×10-23-1 m=2.0×10-2 m,l=4.0 m,d=0.1 mm=1.0×10-4 m,有λ=d·Δxl=5.0×10-7 m,故选B。
二、非选择题
5.答案 1.180 4.8×10-5
解析 根据手轮的读数规则,可得手轮读数为1.180 mm;根据公式Δx=ldλ,解得λ=d·Δxl=4.8×10-7 m=4.8×10-5 cm。
6.答案 (1)甲 (2)CEDBA (3)111.20 6.4×10-7
解析 (1)双缝干涉条纹的特点是等间距、等宽度、等亮度;衍射条纹的特点是中间宽两边窄、中间亮两边暗,且不等间距。根据以上特点知甲图是干涉条纹。
(2)为获取单色线光源,白光光源后面要有滤光片、单缝、双缝,所以各光学元件的排列顺序应为CEDBA。
(3)游标卡尺读数=主尺读数+游标尺读数,故xA=111 mm+0.05 mm×4=111.20 mm,xB=115 mm+0.05 mm×13=115.65 mm;
相邻两个亮条纹的间距Δx=xB-xA7=0.11565-0.111207 m≈0.64 mm
根据公式Δx=Ldλ,有λ=Δx·dL=0.64×10-3×0.50×10-30.50 m=6.4×10-7 m
7.答案 (1)BD (2)11.4 6.0×10-7
解析 (1)若在光屏上得到的图样如题图甲中的(b)图所示,为双缝干涉条纹,则光源和光屏间放置的是双缝挡板,不是单缝挡板,故A错误;若光源和光屏间放置的是双缝挡板,光发生干涉,光源由红光换为蓝光后,依据干涉条纹间距公式Δx=ldλ可知,波长变短,图样的条纹宽度会变窄,故B正确;若光源和光屏间放置的是三棱镜,光源能发出红、绿、紫三色光,光通过三棱镜后,红光偏折最小,则红光最有可能照射到光屏上,紫光偏折最大,则紫光最有可能照射不到光屏上,故C错误,D正确。
(2)由题图丙可知,游标卡尺的示数为11 mm+4×0.1 mm=11.4 mm
相邻两个亮条纹间距为Δx=14×(18.6-11.4) mm=1.8×10-3 m
根据双缝干涉条纹间距公式Δx=ldλ,代入数据解得λ=6.0×10-7 m
8.答案 (1)10.45 2.47 (2)6.2×10-7
解析 (1)刻度尺的分度值为1 mm,需要估读到分度值的下一位,根据刻度尺的读数规则,可得第五条亮条纹中心位置的读数为x5=10.45 cm。
第一条亮条纹中心位置的读数为x1=0.57 cm,则相邻两个亮条纹间距Δx=x5-x14=2.47 cm。
(2)所用双缝的宽度d=0.10 mm=0.000 1 m,双缝到墙面的距离L=80 cm×5=400 cm=4 m,根据干涉条纹间距公式Δx=Ldλ,代入数据解得波长λ=6.2×10-7 m。
9.答案 (1)S经平面镜成的像S' (2)暗条纹 (3)6.33×10-7
解析 (1)如果S被视为双缝中的一个,S经平面镜成的像S'相当于另一个“缝”。
(2)如果把光屏移动到和平面镜接触,入射角接近90°,反射光与入射光相比相位有π的变化,即半波损失,所以接触点P处是暗条纹。
(3)第3条亮条纹到第12条亮条纹的中心间距为22.78 mm,则相邻两个亮条纹间距Δx=22.78×10-39 m=2.53×10-3 m
等效双缝间的距离d=2h=0.30 mm=3×10-4 m,根据双缝干涉条纹间距公式Δx=ldλ,得λ=dΔxD=3×10-4×2.53×10-31.2 m=6.33×10-7 m。
10.答案 S1与S2间的距离 S1(或S2)与光屏间的距离 干涉条纹间距
解析 由题意“光源S发出的光经棱镜作用后,相当于在没有棱镜时,两个分别位于图中S1和S2位置的相干光源所发出的光的叠加”可知,S1与S2相当于双缝干涉实验中的双缝。根据双缝干涉条纹的间距公式Δx=ldλ可知λ=Δx·dl,故需要测量的物理量有:S1与S2间的距离、S1(或S2)与光屏间的距离、干涉条纹间距。
一、选择题
1.用单色光做双缝干涉实验,下列说法正确的是( )
A.相邻两亮条纹或暗条纹的中心间距相等
B.中央亮条纹的宽度是两侧亮条纹宽度的2倍
C.屏与双缝之间的距离减小,则屏上条纹间的距离增大
D.在实验装置不变的情况下,红光的条纹间距小于蓝光的条纹间距
2.用如图所示的装置来观察光的双缝干涉现象时,以下推断正确的是( )
A.狭缝屏的作用是使入射光到达双缝屏时,双缝就成了两个振动情况总是相同的光源
B.若入射光是白光,则像屏上的条纹是黑白相间的干涉条纹
C.屏上某点到双缝的距离差为入射光波长的1.5倍时,该点处一定是亮条纹
D.双缝干涉中亮条纹之间的距离相等,暗条纹之间的距离不相等
3.(多选)在“用双缝干涉测量光的波长”实验中(实验装置如图),下列说法哪些是正确的( )
A.调节光源高度,使光束沿遮光筒轴线照在屏中心时,应放上单缝和双缝
B.测量某条干涉亮条纹位置时,应使分划板中心刻线与该亮条纹的中心对齐
C.为了减小测量误差,可测出n条亮条纹间的距离a,求出相邻两条亮条纹间距Δx=an-1
D.某同学用黄光作为入射光,为了增大干涉条纹的间距,可以采用的方法是改用蓝光作为入射光
4.某次实验中,测得第一级亮条纹和第三级亮条纹中心相距4.0×10-2 m,若双缝间距为0.1 mm,双缝到屏的距离为l=4.0 m,则光波的波长为( )
A.8.0×10-8 m B.5.0×10-7 m
C.1.5×10-8 m D.1.0×10-7 m
5.在“用双缝干涉测量光的波长”的实验中,调节测量头的位置,使分划板中心刻线对齐某亮条纹的中心,如图所示,此时手轮的读数是 mm。转动测量头,使分划板中心刻线向一侧移动到另一条亮条纹中心位置,再次记下手轮上的读数。若实验测得的4条亮条纹中心间的距离为0.960 mm,且已知双缝间距d=1.5 mm,双缝到屏的距离l=100 cm,则对应的光波的波长为λ= cm。?
在用双缝干涉测光的波长的实验中,请按照题目要求回答下列问题。
(1)甲、乙两图都是光的条纹形状示意图,其中干涉图样是 。?
将表中的光学元件放在图丙所示的光具座上,组装成用双缝干涉测光的波长的实验装置,并用此装置测量红光的波长。
161099567310 丙
元件代号
A
B
C
D
E
元件名称
光屏
双缝
白光光源
单缝
透红光的滤光片
将白光光源C放在光具座最左端,依次放置其他光学元件,由左至右,各光学元件的排列顺序应为 。(填写元件代号)?
(3)已知该装置中双缝间距d=0.50 mm,双缝到光屏的距离L=0.50 m,在光屏上得到的干涉图样如图丁所示,分划板的中心刻线在图中A位置时,游标卡尺如图戊所示,则其示数为 mm;分划板的中心刻线在B位置时,游标卡尺如图己所示。由以上所测数据可以得出形成此干涉图样的单色光的波长为 m。?
7.(1)利用图甲(a)所示装置研究光的某些现象,下列说法正确的是 。?
甲
A.若在光屏上得到的图样如图(b)所示,则光源和光屏间放置的是单缝挡板
B.若光源和光屏间放置的是双缝挡板,光源由红光换为蓝光后,图样的条纹宽度会变窄
C.若光源和光屏间放置的是三棱镜,光源能发出红、绿、紫三色光,则红光最有可能照射不到光屏上
D.若光源和光屏间放置的是三棱镜,光源能发出红、绿、紫三色光,则紫光最有可能照射不到光屏上
(2)用双缝干涉测量某单色光的波长时,所得的图样如乙图所示,调节仪器使分划板的中心刻线对准一条亮条纹A的中心,测量头的游标卡尺示数如图丙所示,其读数为 mm;移动手轮使分划板的中心刻线对准另一条亮条纹B的中心,测量头的游标卡尺示数为18.6 mm。已知双缝挡板与光屏间距为0.6 m,双缝相距0.2 mm,则所测单色光的波长为 m。?
乙
丙
8.某同学在实验室找到了一台陈旧的激光器,铭牌已模糊不清,为了测出该激光器发出光的波长,他在实验室中进行了以下操作:
a.将双缝放置在距墙面恰好是5块完整地板砖的位置;
b.用激光器照射双缝,在墙面上得到了如图所示的清晰的干涉条纹。
(1)图中第五条亮条纹中心位置的读数为 cm,相邻两条亮条纹间距Δx= cm;?
(2)已知所用双缝的宽度d=0.10 mm,实验室的地面由“80 cm×80 cm”的地板砖铺成,则该激光器发出光的波长为 m(结果保留2位有效数字)。?
9.洛埃德(H.Lloyd)在1834年提出了一种更简单的观察光的干涉现象的装置——洛埃德镜。如图所示,从单缝S发出的光,一部分入射到平面镜后反射到光屏上,另一部分直接投射到光屏上,在光屏上两光束交叠区域里将出现干涉条纹。单缝S通过平面镜成的像是S'。
(1)通过洛埃德镜在屏上可以观察到明暗相间的干涉条纹,这和双缝干涉实验得到的干涉条纹一致。如果S被视为其中的一个缝, 相当于另一个“缝”。?
(2)实验表明,光从光疏介质射向光密介质界面发生反射时,在入射角接近90°时,反射光与入射光相比,相位有π的变化,即半波损失。如果把光屏移动到和平面镜接触,接触点P处是 (填“亮条纹”或“暗条纹”)。?
(3)实验中,已知单缝S到平面镜的距离为h=0.15 mm,单缝到光屏的距离为D=1.2 m,观测到第3条亮条纹到第12条亮条纹的中心间距为22.78 mm,则该单色光的波长λ= m(结果保留3位有效数字)。?
10.如图所示为“双棱镜干涉”实验装置,S为单色光源。A为一个顶角略小于180°的等腰三角形棱镜,P为光屏,S位于棱镜的对称轴上,光屏与棱镜底边平行。调节光路,可在屏上观察到干涉条纹。这是由于光源S发出的光经棱镜作用后,相当于在没有棱镜时,两个分别位于图中S1和S2位置的相干光源所发出的光的叠加(S1和S2的连线与棱镜底边平行)。已知S1和S2的位置可由其他实验方法确定,类比“双缝干涉测波长”的实验,可以推测出,若要利用“双棱镜干涉”测量光源S发出的单色光的波长,需要测量的物理量是 、 和 。?
答案
一、选择题
1.A 因为相邻两亮条纹或暗条纹的中心间距Δx=ldλ,其中d为双缝间的距离,l为双缝到屏的距离,λ为光波波长,可见相邻两亮条纹或暗条纹之间的距离相等,A正确,B错误。由公式Δx=ldλ可知,l减小,屏上条纹间距减小,C错误。因为λ红>λ蓝,所以Δx红>Δx蓝,D错误。
2.A 狭缝的作用是形成线光源,使得入射光到达双缝屏时,双缝就成了两个振动情况总是相同的光源,故A正确;若入射光是白光,则像屏上产生的条纹是彩色的干涉条纹,故B错误;像屏上某点到双缝的距离差为入射光波长的1.5倍时,该点是振动减弱点,该处一定是暗条纹,故C错误;干涉条纹是等间距的,相邻的两个亮条纹或相邻的两个暗条纹间距相等,故D错误。
3.BC 调节光源高度,使光束沿遮光筒轴线照在屏中心时,不需放单缝和双缝,故A错误。测量某条干涉亮条纹位置时,应使分划板中心刻线与该亮条纹的中心对齐,故B正确。n条亮条纹之间有n-1个间距,相邻两条亮条纹的间距Δx=an-1,故C正确。某同学用黄光作为入射光,根据Δx=ldλ可知,为了增大干涉条纹的间距,应用波长比黄光长的红光或橙光作为入射光,不可以改用波长比黄光短的蓝光作为入射光,故D错误。
4.B 根据公式Δx=ldλ,Δx=4.0×10-23-1 m=2.0×10-2 m,l=4.0 m,d=0.1 mm=1.0×10-4 m,有λ=d·Δxl=5.0×10-7 m,故选B。
二、非选择题
5.答案 1.180 4.8×10-5
解析 根据手轮的读数规则,可得手轮读数为1.180 mm;根据公式Δx=ldλ,解得λ=d·Δxl=4.8×10-7 m=4.8×10-5 cm。
6.答案 (1)甲 (2)CEDBA (3)111.20 6.4×10-7
解析 (1)双缝干涉条纹的特点是等间距、等宽度、等亮度;衍射条纹的特点是中间宽两边窄、中间亮两边暗,且不等间距。根据以上特点知甲图是干涉条纹。
(2)为获取单色线光源,白光光源后面要有滤光片、单缝、双缝,所以各光学元件的排列顺序应为CEDBA。
(3)游标卡尺读数=主尺读数+游标尺读数,故xA=111 mm+0.05 mm×4=111.20 mm,xB=115 mm+0.05 mm×13=115.65 mm;
相邻两个亮条纹的间距Δx=xB-xA7=0.11565-0.111207 m≈0.64 mm
根据公式Δx=Ldλ,有λ=Δx·dL=0.64×10-3×0.50×10-30.50 m=6.4×10-7 m
7.答案 (1)BD (2)11.4 6.0×10-7
解析 (1)若在光屏上得到的图样如题图甲中的(b)图所示,为双缝干涉条纹,则光源和光屏间放置的是双缝挡板,不是单缝挡板,故A错误;若光源和光屏间放置的是双缝挡板,光发生干涉,光源由红光换为蓝光后,依据干涉条纹间距公式Δx=ldλ可知,波长变短,图样的条纹宽度会变窄,故B正确;若光源和光屏间放置的是三棱镜,光源能发出红、绿、紫三色光,光通过三棱镜后,红光偏折最小,则红光最有可能照射到光屏上,紫光偏折最大,则紫光最有可能照射不到光屏上,故C错误,D正确。
(2)由题图丙可知,游标卡尺的示数为11 mm+4×0.1 mm=11.4 mm
相邻两个亮条纹间距为Δx=14×(18.6-11.4) mm=1.8×10-3 m
根据双缝干涉条纹间距公式Δx=ldλ,代入数据解得λ=6.0×10-7 m
8.答案 (1)10.45 2.47 (2)6.2×10-7
解析 (1)刻度尺的分度值为1 mm,需要估读到分度值的下一位,根据刻度尺的读数规则,可得第五条亮条纹中心位置的读数为x5=10.45 cm。
第一条亮条纹中心位置的读数为x1=0.57 cm,则相邻两个亮条纹间距Δx=x5-x14=2.47 cm。
(2)所用双缝的宽度d=0.10 mm=0.000 1 m,双缝到墙面的距离L=80 cm×5=400 cm=4 m,根据干涉条纹间距公式Δx=Ldλ,代入数据解得波长λ=6.2×10-7 m。
9.答案 (1)S经平面镜成的像S' (2)暗条纹 (3)6.33×10-7
解析 (1)如果S被视为双缝中的一个,S经平面镜成的像S'相当于另一个“缝”。
(2)如果把光屏移动到和平面镜接触,入射角接近90°,反射光与入射光相比相位有π的变化,即半波损失,所以接触点P处是暗条纹。
(3)第3条亮条纹到第12条亮条纹的中心间距为22.78 mm,则相邻两个亮条纹间距Δx=22.78×10-39 m=2.53×10-3 m
等效双缝间的距离d=2h=0.30 mm=3×10-4 m,根据双缝干涉条纹间距公式Δx=ldλ,得λ=dΔxD=3×10-4×2.53×10-31.2 m=6.33×10-7 m。
10.答案 S1与S2间的距离 S1(或S2)与光屏间的距离 干涉条纹间距
解析 由题意“光源S发出的光经棱镜作用后,相当于在没有棱镜时,两个分别位于图中S1和S2位置的相干光源所发出的光的叠加”可知,S1与S2相当于双缝干涉实验中的双缝。根据双缝干涉条纹的间距公式Δx=ldλ可知λ=Δx·dl,故需要测量的物理量有:S1与S2间的距离、S1(或S2)与光屏间的距离、干涉条纹间距。
