苏科版八年级上册数学 3.3 勾股定理的简单应用 同步练习(Word版 含解析)
文档属性
| 名称 | 苏科版八年级上册数学 3.3 勾股定理的简单应用 同步练习(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 163.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-20 05:26:51 | ||
图片预览




文档简介
3.3 勾股定理的简单应用 同步练习
一.选择题
1.如图,为测量小区内池塘最宽处A、B两点间的距离,在池塘边定一点C,使∠BAC=90°,并测得AC的长18m,BC的长为30m,则最宽处AB的距离为( )
A.18m B.20m C.22m D.24m
2.小明同学从A地出发,向正北方向走3千米到达B地,然后从B地出发,向正东方向走4千米到达C地.此时他离A地的距离AC是( )
A.7千米 B.5千米 C.4千米 D.3千米
3.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里.若“远航”号沿东北方向航行,则“海天”号沿( )
A.西南方向航行
B.西北方向航行
C.东南方向航行
D.西北方向航行或东南方向航行
4.如图,学校教学楼旁有一块矩形花圃,有极少数同学为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了( )步路(假设2步为1米),却踩伤了花草.
A.6 B.5 C.4 D.3
5.有一长、宽、高分别为5cm、4cm、3cm的木箱,在它里面放入一根细木条(木条的粗细、形变忽略不计)要求木条不能露出木箱.请你算一算,能放入的细木条的最大长度是( )
A.cm B.cm C.cm D.cm
6.园丁住宅小区有一块草坪如图所示.已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,这块草坪的面积是( )
A.24米2 B.36米2 C.48米2 D.72米2
7.长方形门框ABCD中,AB=2m,AD=1.5m.现有四块长方形薄木板,尺寸分别是:①长1.4m,宽1.2m;②长2.1m,宽1.7m;③长2.7m,宽2.1m;④长3m,宽2.6m.其中不能从门框内通过的木板有( )
A.0块 B.1块 C.2块 D.3块
8.如图,小明在广场上先向东走10米,又向南走40米,再向西走20米,又向南走40米,再向东走70米,小明到达的终止点与原出发点的距离为( )米.
A.80 B.100 C.110 D.180
9.如图,一艘船以6海里/小时的速度从港口A出发向东北方向航行,另一艘船以2.5海里/小时的速度同时从港口A出发向东南方向航行,离开港口2小时后,两船相距( )
A.13海里 B.10海里 C.6.5海里 D.5海里
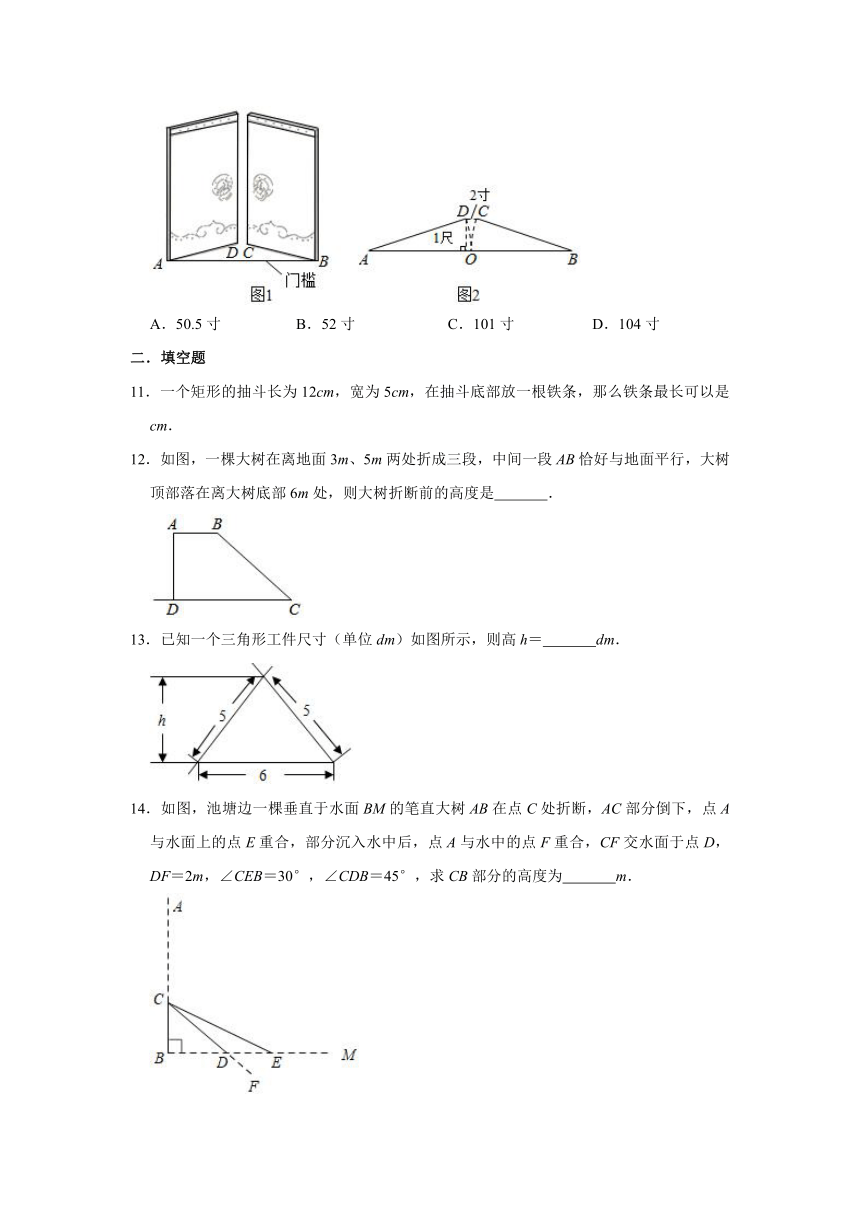
10.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是( )
A.50.5寸 B.52寸 C.101寸 D.104寸
二.填空题
11.一个矩形的抽斗长为12cm,宽为5cm,在抽斗底部放一根铁条,那么铁条最长可以是 cm.
12.如图,一棵大树在离地面3m、5m两处折成三段,中间一段AB恰好与地面平行,大树顶部落在离大树底部6m处,则大树折断前的高度是 .
13.已知一个三角形工件尺寸(单位dm)如图所示,则高h= dm.
14.如图,池塘边一棵垂直于水面BM的笔直大树AB在点C处折断,AC部分倒下,点A与水面上的点E重合,部分沉入水中后,点A与水中的点F重合,CF交水面于点D,DF=2m,∠CEB=30°,∠CDB=45°,求CB部分的高度为 m.
15.如图,是矗立在高速公路地面上的一块交通警示牌,经测量得知PA=4米,AB=5米,∠PAD=45°,∠PBC=30°,则警示牌的高CD为 .(结果保留小数点后一位)
三.解答题
16.如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路CH,测得CB=1.5千米,CH=1.2千米,HB=0.9千米.
(1)问CH是否为从村庄C到河边的最近路?请通过计算加以说明;
(2)求新路CH比原路CA少多少千米?
17.如图,距沿海某城市A正南220千米的B处,有一台风中心,其最大风力为12级,每远离台风中心20千米,风力就减弱1级,该中心正以每小时15千米的速度沿北偏东30°的BC方向移动,且风力不变,若城市A所受风力达到或超过4级,则称为受台风影响.
(1)A城市是否会受台风影响?为什么?
(2)若会,将持续多长时间?
(3)该城市受台风影响的最大风力为几级?
18.如图,在笔直的铁路上A,B两点相距20km,C,D为两村庄,DA=8km,CB=14km,DA⊥AB于A,CB⊥AB于B.现要在AB上建一个中转站E,使得C,D两村到E站的距离相等,求AE的长.
参考答案
1.解:∵∠BAC=90°,并测得AC的长18m,BC的长为30m,
∴由勾股定理得:AB===24m,
故选:D.
2.解:如图:AB=3千米,BC=4千米,根据勾股定理得:AC===5千米.
故选:B.
3.解:一个半小时内“远航”号的航行距离:OB=16×1.5=24海里;
一个半小时内“海天”号的航行距离:OA=12×1.5=18海里,
因为AB=30海里,所以AB2=OB2+OA2,即302=242+182,所以△OAB是直角三角形,
又因为∠1=45°,所以∠2=45°,
故“海天”号沿西北方向航行或东南方向航行.
故选:D.
4.解:根据勾股定理得,斜边的长:=5米,
少走:3+4﹣5=2米,
因为两步为1米,
所以少走了2×2=4步.故选:C.
5.解:由题意可知FG=5cm、EF=4cm、CG=3cm,连接EG、CE,
在直角△EFG中,
EG===cm,
在Rt△EGC中,EG=cm,CG=3cm,
由勾股定理得CE====5cm,
故选:C.
6.解:连接AC,则由勾股定理得AC=5米,因为AC2+DC2=AD2,所以∠ACD=90°.
这块草坪的面积=SRt△ABC+SRt△ACD=AB?BC+AC?DC=(3×4+5×12)=36米2.
故选:B.
7.解:门框的对角线长是:=2.5m.
宽小于或等于2.5m的有:①②③.
故选:B.
8.解:连接AB,作AC⊥BC于C.
∵AC=40+40=80米,
BC=70﹣10=60米,
则AB==100米.
故选B.
本题考查了勾股定理的应用,连接AB,并构造直角三角形是解题的关键.
9.解:
由题意知,AB=2×6海里=12海里,
AC=2×2.5海里=5海里,
∴在直角△ABC中,BC==13海里,
故选:A.
10.解:如图2所示:
由题意得:OA=OB=AD=BC,
设OA=OB=AD=BC=r寸,
则AB=2r,DE=10,OE=CD=1,AE=r﹣1,
在Rt△ADE中,
AE2+DE2=AD2,即(r﹣1)2+102=r2,
解得:r=50.5,
∴2r=101(寸),
∴AB=101寸,
故选:C.
11.解:在直角△ABC中,根据勾股定理可得:AC===13(cm).
即铁条最长可以是13cm.
故答案是:13.
12.解:如图,作BE⊥DC于点E,
由题意得:AD=BE=3m,AB=DE=2m,
∵DC=6m,
∴EC=4m,
∴由勾股定理得:BC==5(m),
∴大树的高度为5+5=10(m),
故答案为:10m.
13.解:
过点A作AD⊥BC于点D,则AD=h,
∵AB=AC=5dm,BC=6dm,
∴AD是BC的垂直平分线,
∴BD=BC=3dm.
在Rt△ABD中,
AD=dm,即h=4(dm).
答:h的长为4dm.
故答案为:4.
14.解:设CB部分的高度为xm.
∵∠BDC=∠BCD=45°,
∴BC=BD=xm.
在Rt△BCD中,CD===x(m).
在Rt△BCE中,∵∠BEC=30°,
∴CE=2BC=2x(m).
∵CE=CF=CD+DF,
∴2x=x+2,
解得:x=2+.
∴BC=(2+)(m).
答:CB部分的高度约为(2+)m,
故答案为:(2+).
15.解:∵∠PAD=45°,∠DPA=90°,
∴∠PDA=45°,
∴DP=AP=4m,
∵∠PBC=30°,AB=8米,
∴tan30°=,
解得:DC=(3﹣4)m≈1.2(米),
答:警示牌的高CD为1.2米.
故答案为:1.2(米).
16.解:(1)是,
理由是:在△CHB中,
∵CH2+BH2=(1.2)2+(0.9)2=2.25,
BC2=2.25,
∴CH2+BH2=BC2,
∴CH⊥AB,
所以CH是从村庄C到河边的最近路;
(2)设AC=x千米,
在Rt△ACH中,由已知得AC=x,AH=x﹣0.9,CH=1.2,
由勾股定理得:AC2=AH2+CH2
∴x2=(x﹣0.9)2+(1.2)2,
解这个方程,得x=1.25,
1.25﹣1.2=0.05(千米)
答:新路CH比原路CA少0.05千米.
17.解:(1)该城市会受到这次台风的影响.
理由是:如图,过A作AD⊥BC于D.在Rt△ABD中,
∵∠ABD=30°,AB=220,
∴,
∵城市受到的风力达到或超过四级,则称受台风影响,
∴受台风影响范围的半径为20×(12﹣4)=160.
∵110<160,
∴该城市会受到这次台风的影响.
(2)如图以A为圆心,160为半径作⊙A交BC于E、F.
则AE=AF=160.
∴台风影响该市持续的路程为:EF=2DE=2=60.
∴台风影响该市的持续时间t=60÷15=4(小时).
(3)∵AD距台风中心最近,
∴该城市受到这次台风最大风力为:12﹣(110÷20)=6.5(级).
18.解:设AE=x,则BE=20﹣x,
由勾股定理得:
在Rt△ADE中,DE2=AD2+AE2=82+x2,
在Rt△BCE中,CE2=BC2+BE2=142+(20﹣x)2,
由题意可知:DE=CE,
所以:82+x2=142+(20﹣x)2,解得:x=13.3
所以,E应建在距A点13.3km.
一.选择题
1.如图,为测量小区内池塘最宽处A、B两点间的距离,在池塘边定一点C,使∠BAC=90°,并测得AC的长18m,BC的长为30m,则最宽处AB的距离为( )
A.18m B.20m C.22m D.24m
2.小明同学从A地出发,向正北方向走3千米到达B地,然后从B地出发,向正东方向走4千米到达C地.此时他离A地的距离AC是( )
A.7千米 B.5千米 C.4千米 D.3千米
3.“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后相距30海里.若“远航”号沿东北方向航行,则“海天”号沿( )
A.西南方向航行
B.西北方向航行
C.东南方向航行
D.西北方向航行或东南方向航行
4.如图,学校教学楼旁有一块矩形花圃,有极少数同学为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了( )步路(假设2步为1米),却踩伤了花草.
A.6 B.5 C.4 D.3
5.有一长、宽、高分别为5cm、4cm、3cm的木箱,在它里面放入一根细木条(木条的粗细、形变忽略不计)要求木条不能露出木箱.请你算一算,能放入的细木条的最大长度是( )
A.cm B.cm C.cm D.cm
6.园丁住宅小区有一块草坪如图所示.已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,这块草坪的面积是( )
A.24米2 B.36米2 C.48米2 D.72米2
7.长方形门框ABCD中,AB=2m,AD=1.5m.现有四块长方形薄木板,尺寸分别是:①长1.4m,宽1.2m;②长2.1m,宽1.7m;③长2.7m,宽2.1m;④长3m,宽2.6m.其中不能从门框内通过的木板有( )
A.0块 B.1块 C.2块 D.3块
8.如图,小明在广场上先向东走10米,又向南走40米,再向西走20米,又向南走40米,再向东走70米,小明到达的终止点与原出发点的距离为( )米.
A.80 B.100 C.110 D.180
9.如图,一艘船以6海里/小时的速度从港口A出发向东北方向航行,另一艘船以2.5海里/小时的速度同时从港口A出发向东南方向航行,离开港口2小时后,两船相距( )
A.13海里 B.10海里 C.6.5海里 D.5海里
10.《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是( )
A.50.5寸 B.52寸 C.101寸 D.104寸
二.填空题
11.一个矩形的抽斗长为12cm,宽为5cm,在抽斗底部放一根铁条,那么铁条最长可以是 cm.
12.如图,一棵大树在离地面3m、5m两处折成三段,中间一段AB恰好与地面平行,大树顶部落在离大树底部6m处,则大树折断前的高度是 .
13.已知一个三角形工件尺寸(单位dm)如图所示,则高h= dm.
14.如图,池塘边一棵垂直于水面BM的笔直大树AB在点C处折断,AC部分倒下,点A与水面上的点E重合,部分沉入水中后,点A与水中的点F重合,CF交水面于点D,DF=2m,∠CEB=30°,∠CDB=45°,求CB部分的高度为 m.
15.如图,是矗立在高速公路地面上的一块交通警示牌,经测量得知PA=4米,AB=5米,∠PAD=45°,∠PBC=30°,则警示牌的高CD为 .(结果保留小数点后一位)
三.解答题
16.如图,在一条东西走向河流的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点H(A、H、B在同一条直线上),并新修一条路CH,测得CB=1.5千米,CH=1.2千米,HB=0.9千米.
(1)问CH是否为从村庄C到河边的最近路?请通过计算加以说明;
(2)求新路CH比原路CA少多少千米?
17.如图,距沿海某城市A正南220千米的B处,有一台风中心,其最大风力为12级,每远离台风中心20千米,风力就减弱1级,该中心正以每小时15千米的速度沿北偏东30°的BC方向移动,且风力不变,若城市A所受风力达到或超过4级,则称为受台风影响.
(1)A城市是否会受台风影响?为什么?
(2)若会,将持续多长时间?
(3)该城市受台风影响的最大风力为几级?
18.如图,在笔直的铁路上A,B两点相距20km,C,D为两村庄,DA=8km,CB=14km,DA⊥AB于A,CB⊥AB于B.现要在AB上建一个中转站E,使得C,D两村到E站的距离相等,求AE的长.
参考答案
1.解:∵∠BAC=90°,并测得AC的长18m,BC的长为30m,
∴由勾股定理得:AB===24m,
故选:D.
2.解:如图:AB=3千米,BC=4千米,根据勾股定理得:AC===5千米.
故选:B.
3.解:一个半小时内“远航”号的航行距离:OB=16×1.5=24海里;
一个半小时内“海天”号的航行距离:OA=12×1.5=18海里,
因为AB=30海里,所以AB2=OB2+OA2,即302=242+182,所以△OAB是直角三角形,
又因为∠1=45°,所以∠2=45°,
故“海天”号沿西北方向航行或东南方向航行.
故选:D.
4.解:根据勾股定理得,斜边的长:=5米,
少走:3+4﹣5=2米,
因为两步为1米,
所以少走了2×2=4步.故选:C.
5.解:由题意可知FG=5cm、EF=4cm、CG=3cm,连接EG、CE,
在直角△EFG中,
EG===cm,
在Rt△EGC中,EG=cm,CG=3cm,
由勾股定理得CE====5cm,
故选:C.
6.解:连接AC,则由勾股定理得AC=5米,因为AC2+DC2=AD2,所以∠ACD=90°.
这块草坪的面积=SRt△ABC+SRt△ACD=AB?BC+AC?DC=(3×4+5×12)=36米2.
故选:B.
7.解:门框的对角线长是:=2.5m.
宽小于或等于2.5m的有:①②③.
故选:B.
8.解:连接AB,作AC⊥BC于C.
∵AC=40+40=80米,
BC=70﹣10=60米,
则AB==100米.
故选B.
本题考查了勾股定理的应用,连接AB,并构造直角三角形是解题的关键.
9.解:
由题意知,AB=2×6海里=12海里,
AC=2×2.5海里=5海里,
∴在直角△ABC中,BC==13海里,
故选:A.
10.解:如图2所示:
由题意得:OA=OB=AD=BC,
设OA=OB=AD=BC=r寸,
则AB=2r,DE=10,OE=CD=1,AE=r﹣1,
在Rt△ADE中,
AE2+DE2=AD2,即(r﹣1)2+102=r2,
解得:r=50.5,
∴2r=101(寸),
∴AB=101寸,
故选:C.
11.解:在直角△ABC中,根据勾股定理可得:AC===13(cm).
即铁条最长可以是13cm.
故答案是:13.
12.解:如图,作BE⊥DC于点E,
由题意得:AD=BE=3m,AB=DE=2m,
∵DC=6m,
∴EC=4m,
∴由勾股定理得:BC==5(m),
∴大树的高度为5+5=10(m),
故答案为:10m.
13.解:
过点A作AD⊥BC于点D,则AD=h,
∵AB=AC=5dm,BC=6dm,
∴AD是BC的垂直平分线,
∴BD=BC=3dm.
在Rt△ABD中,
AD=dm,即h=4(dm).
答:h的长为4dm.
故答案为:4.
14.解:设CB部分的高度为xm.
∵∠BDC=∠BCD=45°,
∴BC=BD=xm.
在Rt△BCD中,CD===x(m).
在Rt△BCE中,∵∠BEC=30°,
∴CE=2BC=2x(m).
∵CE=CF=CD+DF,
∴2x=x+2,
解得:x=2+.
∴BC=(2+)(m).
答:CB部分的高度约为(2+)m,
故答案为:(2+).
15.解:∵∠PAD=45°,∠DPA=90°,
∴∠PDA=45°,
∴DP=AP=4m,
∵∠PBC=30°,AB=8米,
∴tan30°=,
解得:DC=(3﹣4)m≈1.2(米),
答:警示牌的高CD为1.2米.
故答案为:1.2(米).
16.解:(1)是,
理由是:在△CHB中,
∵CH2+BH2=(1.2)2+(0.9)2=2.25,
BC2=2.25,
∴CH2+BH2=BC2,
∴CH⊥AB,
所以CH是从村庄C到河边的最近路;
(2)设AC=x千米,
在Rt△ACH中,由已知得AC=x,AH=x﹣0.9,CH=1.2,
由勾股定理得:AC2=AH2+CH2
∴x2=(x﹣0.9)2+(1.2)2,
解这个方程,得x=1.25,
1.25﹣1.2=0.05(千米)
答:新路CH比原路CA少0.05千米.
17.解:(1)该城市会受到这次台风的影响.
理由是:如图,过A作AD⊥BC于D.在Rt△ABD中,
∵∠ABD=30°,AB=220,
∴,
∵城市受到的风力达到或超过四级,则称受台风影响,
∴受台风影响范围的半径为20×(12﹣4)=160.
∵110<160,
∴该城市会受到这次台风的影响.
(2)如图以A为圆心,160为半径作⊙A交BC于E、F.
则AE=AF=160.
∴台风影响该市持续的路程为:EF=2DE=2=60.
∴台风影响该市的持续时间t=60÷15=4(小时).
(3)∵AD距台风中心最近,
∴该城市受到这次台风最大风力为:12﹣(110÷20)=6.5(级).
18.解:设AE=x,则BE=20﹣x,
由勾股定理得:
在Rt△ADE中,DE2=AD2+AE2=82+x2,
在Rt△BCE中,CE2=BC2+BE2=142+(20﹣x)2,
由题意可知:DE=CE,
所以:82+x2=142+(20﹣x)2,解得:x=13.3
所以,E应建在距A点13.3km.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
