人教版 八年级上册11.1.1 三角形的边课件(19张)
文档属性
| 名称 | 人教版 八年级上册11.1.1 三角形的边课件(19张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-20 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
第十一章
三角形
11.1
与三角形有关的线段
11.1.1
三角形的边
三角形是我们熟悉的图形,观察下列图片,你能说一说三角形是怎样的图形吗?
一、创设情境,引入新知
(一)三角形的定义
由不在同一条直线上的三条线段
首尾顺次相接组成的图形,称为三角形.
不能在同一条直线上.
首尾必须顺次相接.
二、合作交流,探究新知
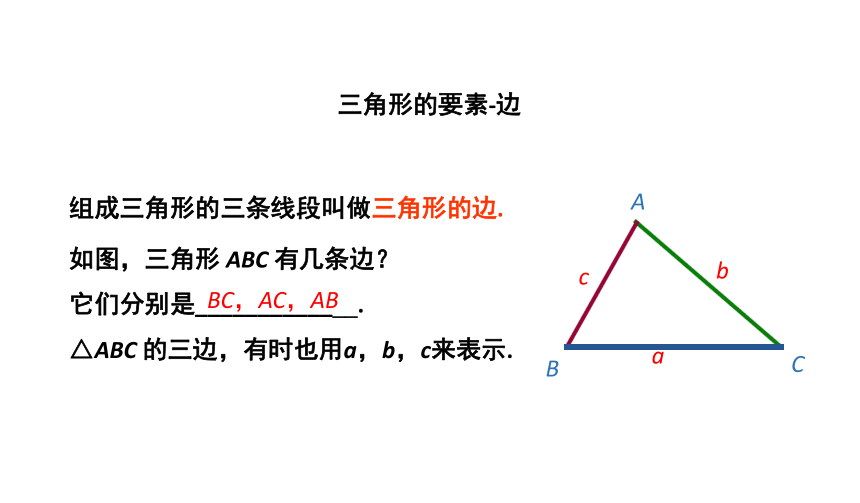
三角形的要素-边
组成三角形的三条线段叫做三角形的边.
如图,三角形
ABC
有几条边?
它们分别是_____________.
△ABC
的三边,有时也用a,b,c来表示.
BC,AC,AB
A
B
C
a
b
c
二、合作交流,探究新知
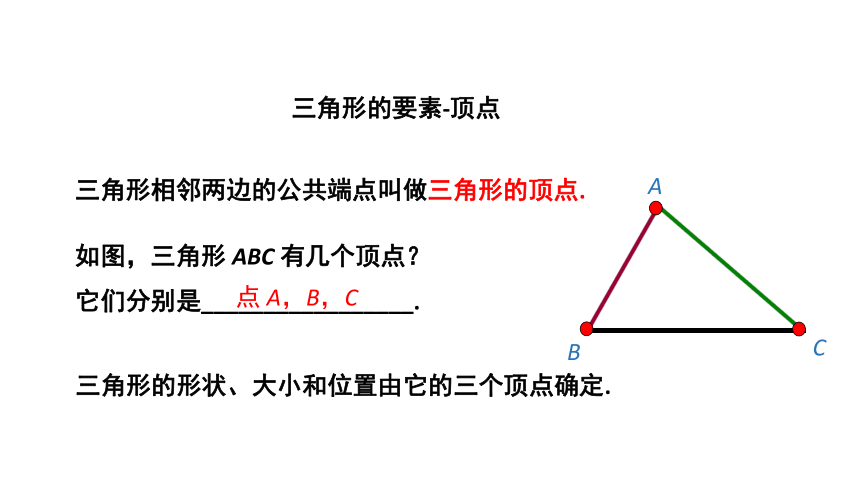
三角形的要素-顶点
三角形相邻两边的公共端点叫做三角形的顶点.
如图,三角形
ABC
有几个顶点?
它们分别是_________________.
点
A,B,C
三角形的形状、大小和位置由它的三个顶点确定.
A
B
C
二、合作交流,探究新知
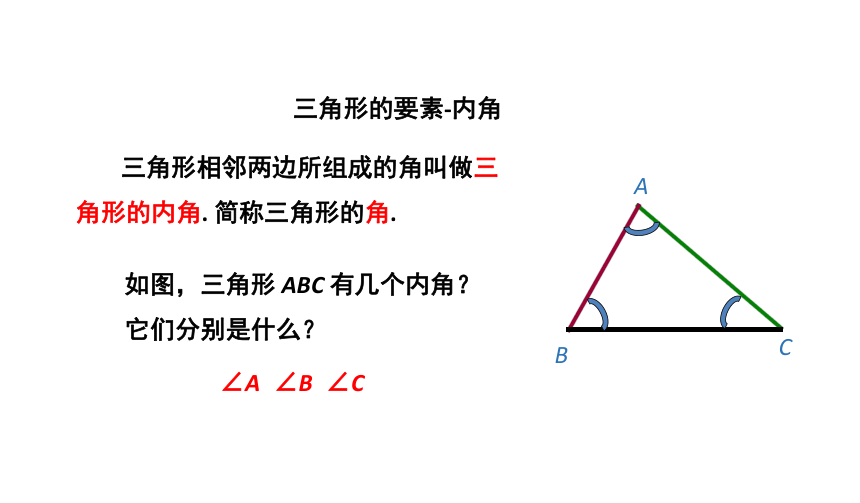
三角形的要素-内角
三角形相邻两边所组成的角叫做三角形的内角.
简称三角形的角.
如图,三角形
ABC
有几个内角?
它们分别是什么?
∠A
A
B
C
∠B
∠C
二、合作交流,探究新知
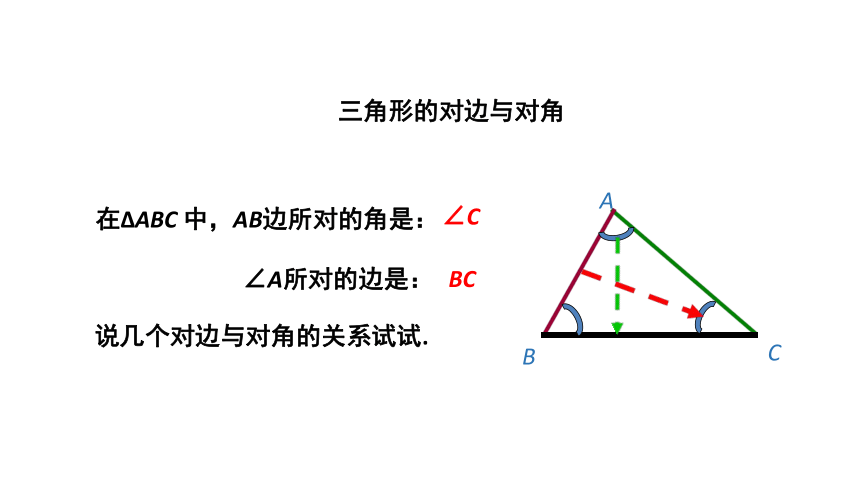
三角形的对边与对角
在?ABC
中,AB边所对的角是:
∠A所对的边是:
∠C
BC
A
B
C
说几个对边与对角的关系试试.
二、合作交流,探究新知
三角形的表示法
我的姓是:“△”
我的名字是:三个顶点字母“A,B,C
”
A
B
C
如:右图的三角形记作:△ABC
(或△BCA
或△CBA
等).
注意:表示三角形时,字母没有先后顺序,但通常按逆时针来排列.
二、合作交流,探究新知
(二)三角形三边的不等关系
任意画一个△ABC,假设有一只小虫要从
B
点出发,沿三角形的边爬到
C,它有几种路线可以选择?各条路线的长一样吗?为什么?
有两条路线:(1)从B→C,(2)从B→A→C;
不一样,
AB+AC>BC
①;
因为两点之间线段最短,
同样地有
AC+BC>AB
②,AB+BC>AC
③.
由式子①②③我们可以知道什么?
三角形的任意两边之和大于第三边.
A
B
C
二、合作交流,探究新知
构成三角形的条件:
只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.
结论:
较小两边之和大于第三边,才能构成三角形.
二、合作交流,探究新知
(三)我们知道,三角形按角可以分为锐角三角形、直角三角形和钝角三角形.
你能按照边的关系对三角形进行分类吗?
三边都不相等的三角形
三角形
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
二、合作交流,探究新知
你能说出它的边、顶点与内角吗?
边:AB,BC,AC
或
c,a,b.
顶点:A,B,C
.
内角:∠A
,∠B
,∠C.
三、运用新知
1.
图中共有_________个三角形,它们分别是
:____________________________________________.
5
△ABE,
△ABC,△BCE,
△BCD
,△CDE
A
B
C
D
E
四、巩固新知
2.
以
AB
为边的三角形有哪些?
3.
以
E
为顶点的三角形有哪些?
4.
以∠D为角的三角形有哪些?
△ABC,△ABE.
△
ABE,△BCE,△CDE.
△
BCD,△DEC.
四、巩固新知
A
B
C
D
E
5.
△BCD的三边分别是:________________
三个角分别是:______________________
三个顶点分别是:____________
其中顶点C的对边是:____
∠D是由____和____两边组成的内角.
∠BEC是△BCD的内角吗?
BC,CD,DB
∠DBC,∠BCD,∠CDB
点D,B,C
DB
DC
DB
不是
四、巩固新知
A
B
C
D
E
小晶有两根长度为
5
cm,8
cm的木条,她想钉一个三角形的木框,现在有长度分别为
2
cm,3
cm,8
cm,15
cm
的木条供她选择,那她第三根应选择?(
)
A.
2
cm
B.
3
cm
C.
8
cm
D.
15
cm
C
分析:
∵
第三根可选择的范围是:
大于8-5=3(cm)小于8+5=13(cm)
∴只有8
cm的木条能钉成三角形木框,
所以答案选C.
解题技巧:
三角形第三边的取值范围是:
两边之差<第三边<两边之和
四、巩固新知
小明有两根长为
10
cm
和
3
cm
的木条,他要钉一个三角形像框,并且使所选择的第三根木条长度是
6
的整数倍.
聪明的你帮他想想,第三根木条应取多长?
解:三角形像框第三边的取值范围是:
∵两边之差
<
第三边
<
两边之和,
即10-3
<
x
<
10+3,解得7
<
x
<
13.
符合条件的数是
12.
∴第三根木条应取
12
cm.
四、巩固新知
三角形:
三角形有基本要素:
基本要素
边
(AB,BC,CA)
角
顶点
(A,B,C)
(∠A,∠B,∠C)
三角形的表示:
用符号“△”表示,如上面的三角形ABC,记作:△ABC.
由不在同一直线上的三条线段首尾顺次相接所组成的图形.
五、归纳小结
A
B
C
1.
三角形的三边关系:
三角形的任何两边的和大于第三边.
两边之差<第三边<两边之和.
2.
判断三条已知线段能否组成三角形时,采用一种较为简便的方法:
若最短边与较长边的和大于最长边,则可构成三角形,否则不能.
3.
确定三角形第三边的取值范围:
五、归纳小结
第十一章
三角形
11.1
与三角形有关的线段
11.1.1
三角形的边
三角形是我们熟悉的图形,观察下列图片,你能说一说三角形是怎样的图形吗?
一、创设情境,引入新知
(一)三角形的定义
由不在同一条直线上的三条线段
首尾顺次相接组成的图形,称为三角形.
不能在同一条直线上.
首尾必须顺次相接.
二、合作交流,探究新知
三角形的要素-边
组成三角形的三条线段叫做三角形的边.
如图,三角形
ABC
有几条边?
它们分别是_____________.
△ABC
的三边,有时也用a,b,c来表示.
BC,AC,AB
A
B
C
a
b
c
二、合作交流,探究新知
三角形的要素-顶点
三角形相邻两边的公共端点叫做三角形的顶点.
如图,三角形
ABC
有几个顶点?
它们分别是_________________.
点
A,B,C
三角形的形状、大小和位置由它的三个顶点确定.
A
B
C
二、合作交流,探究新知
三角形的要素-内角
三角形相邻两边所组成的角叫做三角形的内角.
简称三角形的角.
如图,三角形
ABC
有几个内角?
它们分别是什么?
∠A
A
B
C
∠B
∠C
二、合作交流,探究新知
三角形的对边与对角
在?ABC
中,AB边所对的角是:
∠A所对的边是:
∠C
BC
A
B
C
说几个对边与对角的关系试试.
二、合作交流,探究新知
三角形的表示法
我的姓是:“△”
我的名字是:三个顶点字母“A,B,C
”
A
B
C
如:右图的三角形记作:△ABC
(或△BCA
或△CBA
等).
注意:表示三角形时,字母没有先后顺序,但通常按逆时针来排列.
二、合作交流,探究新知
(二)三角形三边的不等关系
任意画一个△ABC,假设有一只小虫要从
B
点出发,沿三角形的边爬到
C,它有几种路线可以选择?各条路线的长一样吗?为什么?
有两条路线:(1)从B→C,(2)从B→A→C;
不一样,
AB+AC>BC
①;
因为两点之间线段最短,
同样地有
AC+BC>AB
②,AB+BC>AC
③.
由式子①②③我们可以知道什么?
三角形的任意两边之和大于第三边.
A
B
C
二、合作交流,探究新知
构成三角形的条件:
只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.
结论:
较小两边之和大于第三边,才能构成三角形.
二、合作交流,探究新知
(三)我们知道,三角形按角可以分为锐角三角形、直角三角形和钝角三角形.
你能按照边的关系对三角形进行分类吗?
三边都不相等的三角形
三角形
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
二、合作交流,探究新知
你能说出它的边、顶点与内角吗?
边:AB,BC,AC
或
c,a,b.
顶点:A,B,C
.
内角:∠A
,∠B
,∠C.
三、运用新知
1.
图中共有_________个三角形,它们分别是
:____________________________________________.
5
△ABE,
△ABC,△BCE,
△BCD
,△CDE
A
B
C
D
E
四、巩固新知
2.
以
AB
为边的三角形有哪些?
3.
以
E
为顶点的三角形有哪些?
4.
以∠D为角的三角形有哪些?
△ABC,△ABE.
△
ABE,△BCE,△CDE.
△
BCD,△DEC.
四、巩固新知
A
B
C
D
E
5.
△BCD的三边分别是:________________
三个角分别是:______________________
三个顶点分别是:____________
其中顶点C的对边是:____
∠D是由____和____两边组成的内角.
∠BEC是△BCD的内角吗?
BC,CD,DB
∠DBC,∠BCD,∠CDB
点D,B,C
DB
DC
DB
不是
四、巩固新知
A
B
C
D
E
小晶有两根长度为
5
cm,8
cm的木条,她想钉一个三角形的木框,现在有长度分别为
2
cm,3
cm,8
cm,15
cm
的木条供她选择,那她第三根应选择?(
)
A.
2
cm
B.
3
cm
C.
8
cm
D.
15
cm
C
分析:
∵
第三根可选择的范围是:
大于8-5=3(cm)小于8+5=13(cm)
∴只有8
cm的木条能钉成三角形木框,
所以答案选C.
解题技巧:
三角形第三边的取值范围是:
两边之差<第三边<两边之和
四、巩固新知
小明有两根长为
10
cm
和
3
cm
的木条,他要钉一个三角形像框,并且使所选择的第三根木条长度是
6
的整数倍.
聪明的你帮他想想,第三根木条应取多长?
解:三角形像框第三边的取值范围是:
∵两边之差
<
第三边
<
两边之和,
即10-3
<
x
<
10+3,解得7
<
x
<
13.
符合条件的数是
12.
∴第三根木条应取
12
cm.
四、巩固新知
三角形:
三角形有基本要素:
基本要素
边
(AB,BC,CA)
角
顶点
(A,B,C)
(∠A,∠B,∠C)
三角形的表示:
用符号“△”表示,如上面的三角形ABC,记作:△ABC.
由不在同一直线上的三条线段首尾顺次相接所组成的图形.
五、归纳小结
A
B
C
1.
三角形的三边关系:
三角形的任何两边的和大于第三边.
两边之差<第三边<两边之和.
2.
判断三条已知线段能否组成三角形时,采用一种较为简便的方法:
若最短边与较长边的和大于最长边,则可构成三角形,否则不能.
3.
确定三角形第三边的取值范围:
五、归纳小结
