人教版九年级数学上册 22.1.3 二次函数y=a (x-h)2+k的平移学案(无答案)
文档属性
| 名称 | 人教版九年级数学上册 22.1.3 二次函数y=a (x-h)2+k的平移学案(无答案) | 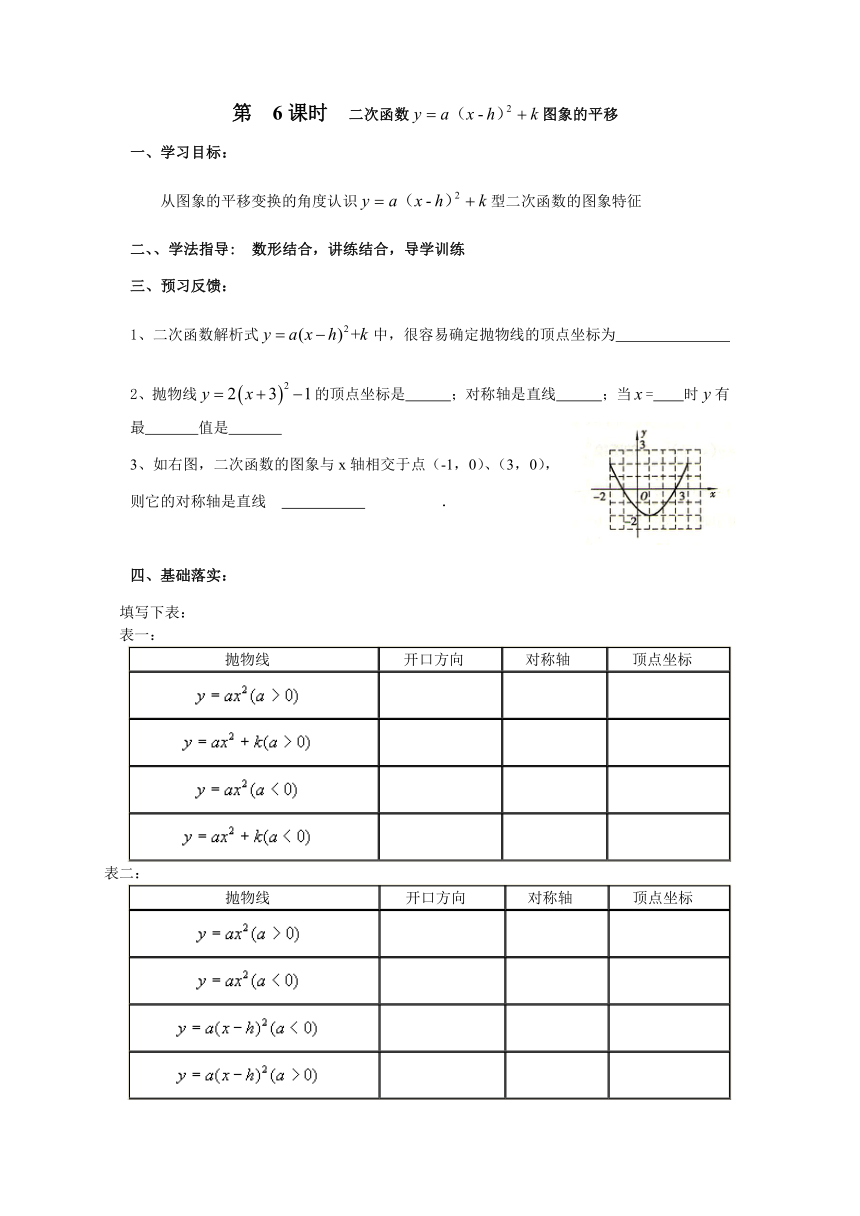 | |
| 格式 | zip | ||
| 文件大小 | 183.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-20 23:33:17 | ||
图片预览

文档简介
学习目标:
从图象的平移变换的角度认识型二次函数的图象特征
二、、学法指导:
数形结合,讲练结合,导学训练
三、预习反馈:
1、二次函数解析式中,很容易确定抛物线的顶点坐标为
2、抛物线的顶点坐标是
;对称轴是直线
;当=
时有最
值是
3、如右图,二次函数的图象与x轴相交于点(-1,0)、(3,0),
则它的对称轴是直线
.
基础落实:
填写下表:
表一:
抛物线
开口方向
对称轴
顶点坐标
?
?
?
?
?
?
?
?
?
?
?
?
表二:
抛物线
开口方向
对称轴
顶点坐标
?
?
?
?
?
?
?
?
?
?
?
?
(a>0)
1.填表:
开口方向
顶点
对称轴
y=2x2
y=2x2+1
y=2
(x-3)2
y=2
(x-3)2+4
2、函数y=x2-3是由y=x2向_____平移_____单位得到的。
3、函数y=x2+1是由y=x2-2向_____平移_____单位得到的。
4、函数y=x2-4是由y=x2+5向_____平移_____单位得到的。
5、函数y=(x-3)2是由y=x2向_____平移_____单位得到的。
6、抛物线的开口
,对称轴是
,顶点坐标是
,它可以看作是由抛物线向
平移
个单位得到的.
7、(1)二次函数y=2(x+5)2的图像是
,开口
,对称轴是
,当x=
时,y有最
值,是
.
(2)二次函数y=-3(x-4)2的图像是由抛物线y=
-3x2向
平移
个单位得到的;开口
,对称轴是
,当x=
时,y有最
值,是
(3)将二次函数y=2x2的图像向右平移3个单位后得到函数
的图像,其对称轴是
,顶点是
,当x
时,y随x的增大而增大;当x
时,y随x的增大而减小。
8、将抛物线y=2
(x+1)2-3向右平移1个单位,再向上平移3个单位,则所得抛物线的表达式为________________________;
巩固提高:
1、抛物线
开口方向
顶点坐标
对称轴
最值
y=-3(x-2)2+1
y=-3(x-3)2-2
y=-(x-4)2+5
y=(x+3)2-4
2、已知抛物线的顶点在坐标轴上,求的值.
六、达标检测:
1.抛物线y=6x2+3与y=6
(x-1)2+10_____________相同,而____________不同.
2.顶点坐标为(-2,3),开口方向和大小与抛物线y=x2相同的解析式为(
)
A.y=(x-2)2+3
;
B.y=(x+2)2-3
;
C.y=(x+2)2+3
;
D.y=-(x+2)2+3
3.二次函数y=(x-1)2+2的最小值为__________________.
从图象的平移变换的角度认识型二次函数的图象特征
二、、学法指导:
数形结合,讲练结合,导学训练
三、预习反馈:
1、二次函数解析式中,很容易确定抛物线的顶点坐标为
2、抛物线的顶点坐标是
;对称轴是直线
;当=
时有最
值是
3、如右图,二次函数的图象与x轴相交于点(-1,0)、(3,0),
则它的对称轴是直线
.
基础落实:
填写下表:
表一:
抛物线
开口方向
对称轴
顶点坐标
?
?
?
?
?
?
?
?
?
?
?
?
表二:
抛物线
开口方向
对称轴
顶点坐标
?
?
?
?
?
?
?
?
?
?
?
?
(a>0)
1.填表:
开口方向
顶点
对称轴
y=2x2
y=2x2+1
y=2
(x-3)2
y=2
(x-3)2+4
2、函数y=x2-3是由y=x2向_____平移_____单位得到的。
3、函数y=x2+1是由y=x2-2向_____平移_____单位得到的。
4、函数y=x2-4是由y=x2+5向_____平移_____单位得到的。
5、函数y=(x-3)2是由y=x2向_____平移_____单位得到的。
6、抛物线的开口
,对称轴是
,顶点坐标是
,它可以看作是由抛物线向
平移
个单位得到的.
7、(1)二次函数y=2(x+5)2的图像是
,开口
,对称轴是
,当x=
时,y有最
值,是
.
(2)二次函数y=-3(x-4)2的图像是由抛物线y=
-3x2向
平移
个单位得到的;开口
,对称轴是
,当x=
时,y有最
值,是
(3)将二次函数y=2x2的图像向右平移3个单位后得到函数
的图像,其对称轴是
,顶点是
,当x
时,y随x的增大而增大;当x
时,y随x的增大而减小。
8、将抛物线y=2
(x+1)2-3向右平移1个单位,再向上平移3个单位,则所得抛物线的表达式为________________________;
巩固提高:
1、抛物线
开口方向
顶点坐标
对称轴
最值
y=-3(x-2)2+1
y=-3(x-3)2-2
y=-(x-4)2+5
y=(x+3)2-4
2、已知抛物线的顶点在坐标轴上,求的值.
六、达标检测:
1.抛物线y=6x2+3与y=6
(x-1)2+10_____________相同,而____________不同.
2.顶点坐标为(-2,3),开口方向和大小与抛物线y=x2相同的解析式为(
)
A.y=(x-2)2+3
;
B.y=(x+2)2-3
;
C.y=(x+2)2+3
;
D.y=-(x+2)2+3
3.二次函数y=(x-1)2+2的最小值为__________________.
同课章节目录
