人教版数学八年级上册课时过关练习13.1.2《线段垂直平分线的性质》(word含答案)
文档属性
| 名称 | 人教版数学八年级上册课时过关练习13.1.2《线段垂直平分线的性质》(word含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 168.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-20 06:40:36 | ||
图片预览


文档简介
人教版八年级上册数学《线段垂直平分线的性质》
课时过关练习
一.选择题.
1.
P是线段AB的垂直平分线上的点,PA=10
cm,则PB等于
(
)
A.10
cm
B.20
cm
C.5
cm
D.不能确定
2.如图,在△ABC中,分别以点A,B为圆心,大于AB长为半径画弧,两弧分别交于点D,E,则直线DE是(
)
A.∠A的平分线
B.AC边的中线
C.BC边的高线
D.AB边的垂直平分线
3.如图,分别以线段AB的两端点A,B为圆心,大于AB长为半径画弧,在线段AB的两侧分别交于点E,F,作直线EF交AB于点O.在直线EF上任取一点P(不与O重合),连接PA,PB,则下列结论不一定成立的是
(
)
A.PA=PB B.OA=OB C.OP=OF D.PO⊥AB
4.如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是
(
)
A.12
B.13
C.14
D.15
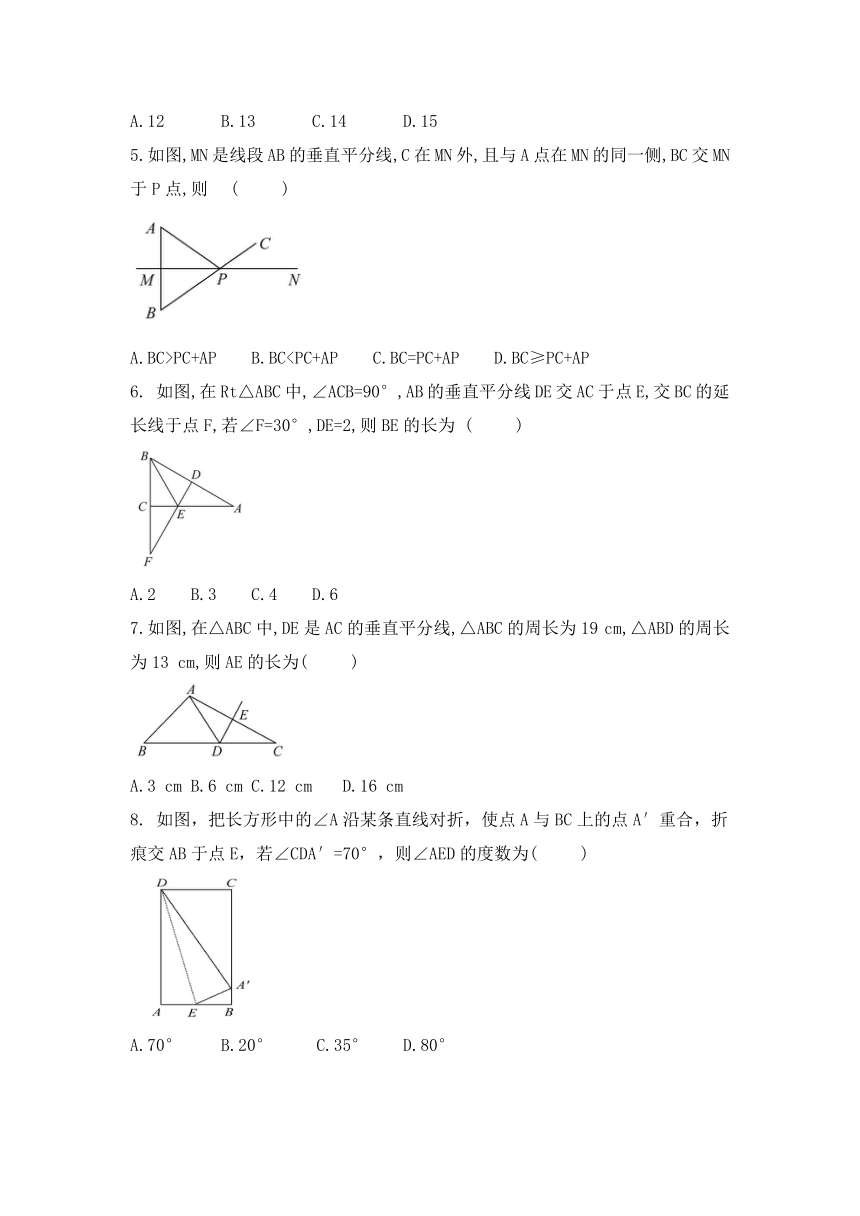
5.如图,MN是线段AB的垂直平分线,C在MN外,且与A点在MN的同一侧,BC交MN于P点,则
(
)
A.BC>PC+AP
B.BCC.BC=PC+AP
D.BC≥PC+AP
6.
如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于点E,交BC的延长线于点F,若∠F=30°,DE=2,则BE的长为
(
)
A.2
B.3
C.4
D.6
7.如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19
cm,△ABD的周长为13
cm,则AE的长为(
)
A.3
cm
B.6
cm
C.12
cm
D.16
cm
8.
如图,把长方形中的∠A沿某条直线对折,使点A与BC上的点A′重合,折痕交AB于点E,若∠CDA′=70°,则∠AED的度数为(
)
A.70°
B.20°
C.35°
D.80°
二.填空题.
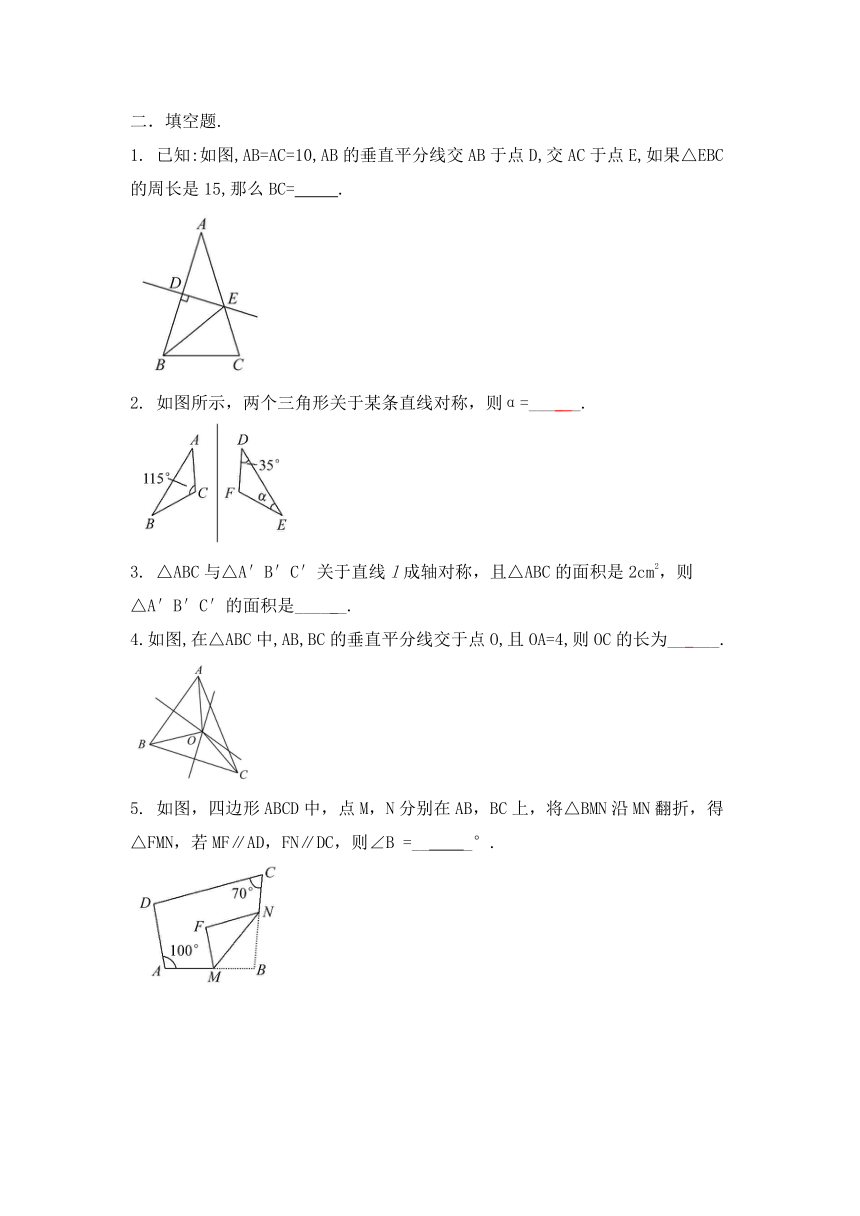
1.
已知:如图,AB=AC=10,AB的垂直平分线交AB于点D,交AC于点E,如果△EBC的周长是15,那么BC=
.?
2.
如图所示,两个三角形关于某条直线对称,则α=____
_.
3.
△ABC与△A′B′C′关于直线l成轴对称,且△ABC的面积是2cm2,则
△A′B′C′的面积是____
_.
4.如图,在△ABC中,AB,BC的垂直平分线交于点O,且OA=4,则OC的长为__
___.
5.
如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B
=__
_°.
三.解答题.
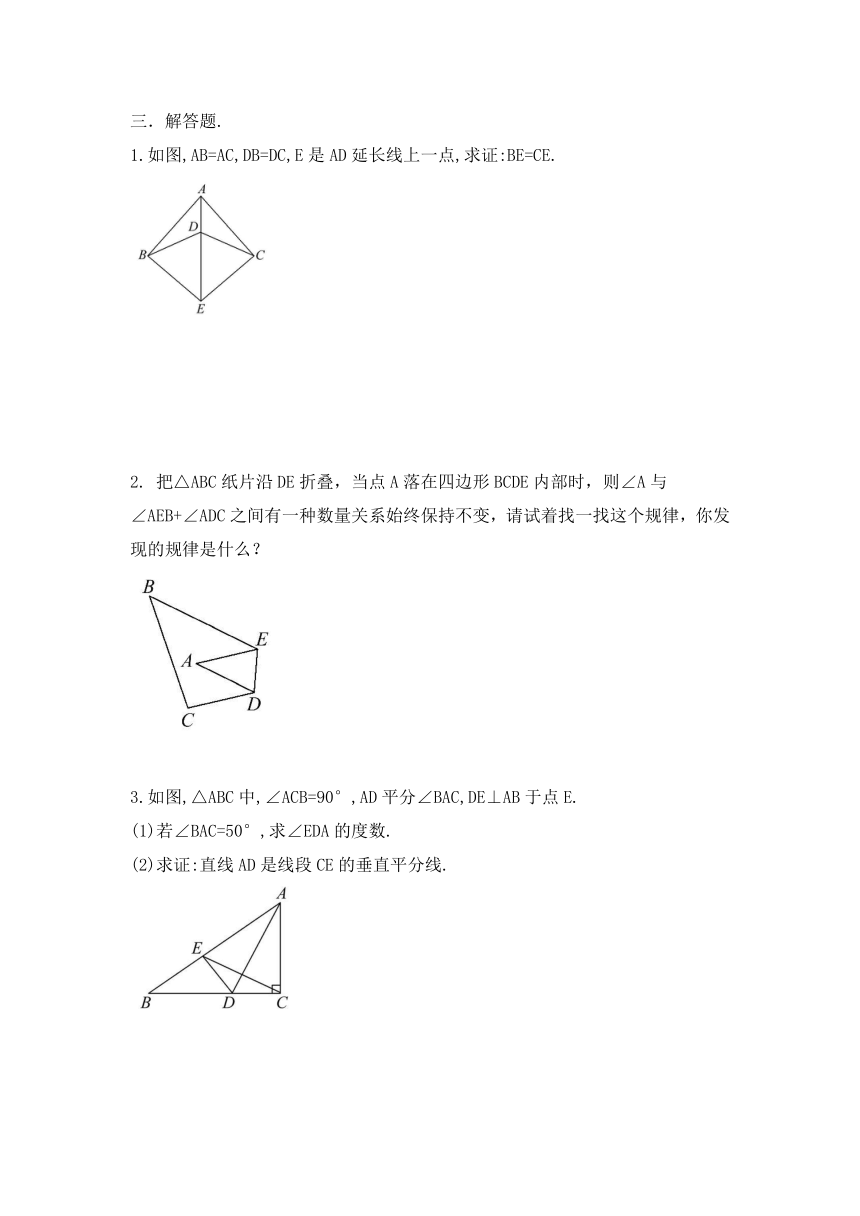
1.如图,AB=AC,DB=DC,E是AD延长线上一点,求证:BE=CE.
2.
把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与
∠AEB+∠ADC之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是什么?
3.如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于点E.
(1)若∠BAC=50°,求∠EDA的度数.
(2)求证:直线AD是线段CE的垂直平分线.
4.在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O.△ADE的周长为8
cm.
(1)求BC的长.
(2)分别连接OA、OB、OC,若△OBC的周长为18
cm,求OA的长.
人教版八年级上册数学《线段垂直平分线的性质》
课时过关练习(解析版)
一.选择题.
1.
P是线段AB的垂直平分线上的点,PA=10
cm,则PB等于
( A )
A.10
cm
B.20
cm
C.5
cm
D.不能确定
2.如图,在△ABC中,分别以点A,B为圆心,大于AB长为半径画弧,两弧分别交于点D,E,则直线DE是( D )
A.∠A的平分线
B.AC边的中线
C.BC边的高线
D.AB边的垂直平分线
3.如图,分别以线段AB的两端点A,B为圆心,大于AB长为半径画弧,在线段AB的两侧分别交于点E,F,作直线EF交AB于点O.在直线EF上任取一点P(不与O重合),连接PA,PB,则下列结论不一定成立的是
( C )
A.PA=PB B.OA=OB C.OP=OF D.PO⊥AB
4.如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是
( B )
A.12
B.13
C.14
D.15
5.如图,MN是线段AB的垂直平分线,C在MN外,且与A点在MN的同一侧,BC交MN于P点,则
( C )
A.BC>PC+AP
B.BCC.BC=PC+AP
D.BC≥PC+AP
6.
如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于点E,交BC的延长线于点F,若∠F=30°,DE=2,则BE的长为
( C )
A.2
B.3
C.4
D.6
7.如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19
cm,△ABD的周长为13
cm,则AE的长为( A )
A.3
cm
B.6
cm
C.12
cm
D.16
cm
8.
如图,把长方形中的∠A沿某条直线对折,使点A与BC上的点A′重合,折痕交AB于点E,若∠CDA′=70°,则∠AED的度数为( D )
A.70°
B.20°
C.35°
D.80°
二.填空题.
1.
已知:如图,AB=AC=10,AB的垂直平分线交AB于点D,交AC于点E,如果△EBC的周长是15,那么BC= 5 .?
2.
如图所示,两个三角形关于某条直线对称,则α=____30°_.
3.
△ABC与△A′B′C′关于直线l成轴对称,且△ABC的面积是2cm2,则
△A′B′C′的面积是____2cm2___.
4.如图,在△ABC中,AB,BC的垂直平分线交于点O,且OA=4,则OC的长为__4____.
5.
如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B
=___95___°.
三.解答题.
1.如图,AB=AC,DB=DC,E是AD延长线上一点,求证:BE=CE.
【证明】连接BC,∵AB=AC,DB=DC,
∴A在线段BC的垂直平分线上,D在线段BC的垂直平分线上,
即AD是线段BC的垂直平分线,
∵E在直线AD上,
∴BE=CE.
2.
把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与
∠AEB+∠ADC之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是什么?
【解析】如图,根据轴对称性质得:
∠1=∠2,∠3=∠4,∠1+∠3+∠A=180°,
所以∠1+∠2+∠3+∠4=360°-2∠A.
因为∠1+∠2+∠3+∠4=2×180°-∠AEB-∠ADC,所以2∠A=∠AEB+∠ADC.
3.如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于点E.
(1)若∠BAC=50°,求∠EDA的度数.
(2)求证:直线AD是线段CE的垂直平分线.
【解析】(1)∵∠BAC=50°,AD平分∠BAC,∴∠EAD=∠BAC=25°,
∵DE⊥AB,∴∠AED=90°,∴∠EDA=90°-25°=65°.
(2)∵DE⊥AB,∴∠AED=90°=∠ACB,又∵AD平分∠BAC,∴∠DAE=∠DAC,
∵AD=AD,∴△AED≌△ACD,∴AE=AC,∵AD平分∠BAC,∴AD⊥CE,即直线AD是线段CE的垂直平分线.
4.在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O.△ADE的周长为8
cm.
(1)求BC的长.
(2)分别连接OA、OB、OC,若△OBC的周长为18
cm,求OA的长.
【解析】(1)∵DO、EO分别是线段AB、AC的垂直平分线,∴AD=BD,AE=CE,
∴AD+DE+AE=BD+DE+CE=BC,∵△ADE的周长为8
cm,即AD+DE+AE=8
cm,
∴BC=8
cm.
(2)∵AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,
∴OA=OC=OB,∵△OBC的周长为18
cm,即OC+OB+BC=18
cm,∴OC+OB=18-8=10(cm),∴OA=OC=OB=5
cm.
课时过关练习
一.选择题.
1.
P是线段AB的垂直平分线上的点,PA=10
cm,则PB等于
(
)
A.10
cm
B.20
cm
C.5
cm
D.不能确定
2.如图,在△ABC中,分别以点A,B为圆心,大于AB长为半径画弧,两弧分别交于点D,E,则直线DE是(
)
A.∠A的平分线
B.AC边的中线
C.BC边的高线
D.AB边的垂直平分线
3.如图,分别以线段AB的两端点A,B为圆心,大于AB长为半径画弧,在线段AB的两侧分别交于点E,F,作直线EF交AB于点O.在直线EF上任取一点P(不与O重合),连接PA,PB,则下列结论不一定成立的是
(
)
A.PA=PB B.OA=OB C.OP=OF D.PO⊥AB
4.如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是
(
)
A.12
B.13
C.14
D.15
5.如图,MN是线段AB的垂直平分线,C在MN外,且与A点在MN的同一侧,BC交MN于P点,则
(
)
A.BC>PC+AP
B.BC
D.BC≥PC+AP
6.
如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于点E,交BC的延长线于点F,若∠F=30°,DE=2,则BE的长为
(
)
A.2
B.3
C.4
D.6
7.如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19
cm,△ABD的周长为13
cm,则AE的长为(
)
A.3
cm
B.6
cm
C.12
cm
D.16
cm
8.
如图,把长方形中的∠A沿某条直线对折,使点A与BC上的点A′重合,折痕交AB于点E,若∠CDA′=70°,则∠AED的度数为(
)
A.70°
B.20°
C.35°
D.80°
二.填空题.
1.
已知:如图,AB=AC=10,AB的垂直平分线交AB于点D,交AC于点E,如果△EBC的周长是15,那么BC=
.?
2.
如图所示,两个三角形关于某条直线对称,则α=____
_.
3.
△ABC与△A′B′C′关于直线l成轴对称,且△ABC的面积是2cm2,则
△A′B′C′的面积是____
_.
4.如图,在△ABC中,AB,BC的垂直平分线交于点O,且OA=4,则OC的长为__
___.
5.
如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B
=__
_°.
三.解答题.
1.如图,AB=AC,DB=DC,E是AD延长线上一点,求证:BE=CE.
2.
把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与
∠AEB+∠ADC之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是什么?
3.如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于点E.
(1)若∠BAC=50°,求∠EDA的度数.
(2)求证:直线AD是线段CE的垂直平分线.
4.在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O.△ADE的周长为8
cm.
(1)求BC的长.
(2)分别连接OA、OB、OC,若△OBC的周长为18
cm,求OA的长.
人教版八年级上册数学《线段垂直平分线的性质》
课时过关练习(解析版)
一.选择题.
1.
P是线段AB的垂直平分线上的点,PA=10
cm,则PB等于
( A )
A.10
cm
B.20
cm
C.5
cm
D.不能确定
2.如图,在△ABC中,分别以点A,B为圆心,大于AB长为半径画弧,两弧分别交于点D,E,则直线DE是( D )
A.∠A的平分线
B.AC边的中线
C.BC边的高线
D.AB边的垂直平分线
3.如图,分别以线段AB的两端点A,B为圆心,大于AB长为半径画弧,在线段AB的两侧分别交于点E,F,作直线EF交AB于点O.在直线EF上任取一点P(不与O重合),连接PA,PB,则下列结论不一定成立的是
( C )
A.PA=PB B.OA=OB C.OP=OF D.PO⊥AB
4.如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是
( B )
A.12
B.13
C.14
D.15
5.如图,MN是线段AB的垂直平分线,C在MN外,且与A点在MN的同一侧,BC交MN于P点,则
( C )
A.BC>PC+AP
B.BC
D.BC≥PC+AP
6.
如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于点E,交BC的延长线于点F,若∠F=30°,DE=2,则BE的长为
( C )
A.2
B.3
C.4
D.6
7.如图,在△ABC中,DE是AC的垂直平分线,△ABC的周长为19
cm,△ABD的周长为13
cm,则AE的长为( A )
A.3
cm
B.6
cm
C.12
cm
D.16
cm
8.
如图,把长方形中的∠A沿某条直线对折,使点A与BC上的点A′重合,折痕交AB于点E,若∠CDA′=70°,则∠AED的度数为( D )
A.70°
B.20°
C.35°
D.80°
二.填空题.
1.
已知:如图,AB=AC=10,AB的垂直平分线交AB于点D,交AC于点E,如果△EBC的周长是15,那么BC= 5 .?
2.
如图所示,两个三角形关于某条直线对称,则α=____30°_.
3.
△ABC与△A′B′C′关于直线l成轴对称,且△ABC的面积是2cm2,则
△A′B′C′的面积是____2cm2___.
4.如图,在△ABC中,AB,BC的垂直平分线交于点O,且OA=4,则OC的长为__4____.
5.
如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B
=___95___°.
三.解答题.
1.如图,AB=AC,DB=DC,E是AD延长线上一点,求证:BE=CE.
【证明】连接BC,∵AB=AC,DB=DC,
∴A在线段BC的垂直平分线上,D在线段BC的垂直平分线上,
即AD是线段BC的垂直平分线,
∵E在直线AD上,
∴BE=CE.
2.
把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与
∠AEB+∠ADC之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是什么?
【解析】如图,根据轴对称性质得:
∠1=∠2,∠3=∠4,∠1+∠3+∠A=180°,
所以∠1+∠2+∠3+∠4=360°-2∠A.
因为∠1+∠2+∠3+∠4=2×180°-∠AEB-∠ADC,所以2∠A=∠AEB+∠ADC.
3.如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于点E.
(1)若∠BAC=50°,求∠EDA的度数.
(2)求证:直线AD是线段CE的垂直平分线.
【解析】(1)∵∠BAC=50°,AD平分∠BAC,∴∠EAD=∠BAC=25°,
∵DE⊥AB,∴∠AED=90°,∴∠EDA=90°-25°=65°.
(2)∵DE⊥AB,∴∠AED=90°=∠ACB,又∵AD平分∠BAC,∴∠DAE=∠DAC,
∵AD=AD,∴△AED≌△ACD,∴AE=AC,∵AD平分∠BAC,∴AD⊥CE,即直线AD是线段CE的垂直平分线.
4.在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O.△ADE的周长为8
cm.
(1)求BC的长.
(2)分别连接OA、OB、OC,若△OBC的周长为18
cm,求OA的长.
【解析】(1)∵DO、EO分别是线段AB、AC的垂直平分线,∴AD=BD,AE=CE,
∴AD+DE+AE=BD+DE+CE=BC,∵△ADE的周长为8
cm,即AD+DE+AE=8
cm,
∴BC=8
cm.
(2)∵AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,
∴OA=OC=OB,∵△OBC的周长为18
cm,即OC+OB+BC=18
cm,∴OC+OB=18-8=10(cm),∴OA=OC=OB=5
cm.
