人教版九年级数学上册 23.3 旋转课题学习 图案设计 课后练习(Word版含答案)
文档属性
| 名称 | 人教版九年级数学上册 23.3 旋转课题学习 图案设计 课后练习(Word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 393.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-20 07:33:10 | ||
图片预览


文档简介
人教版九年级数学上册
第二十三章
旋转
23.3
课题学习
图案设计
课后练习
一、选择题
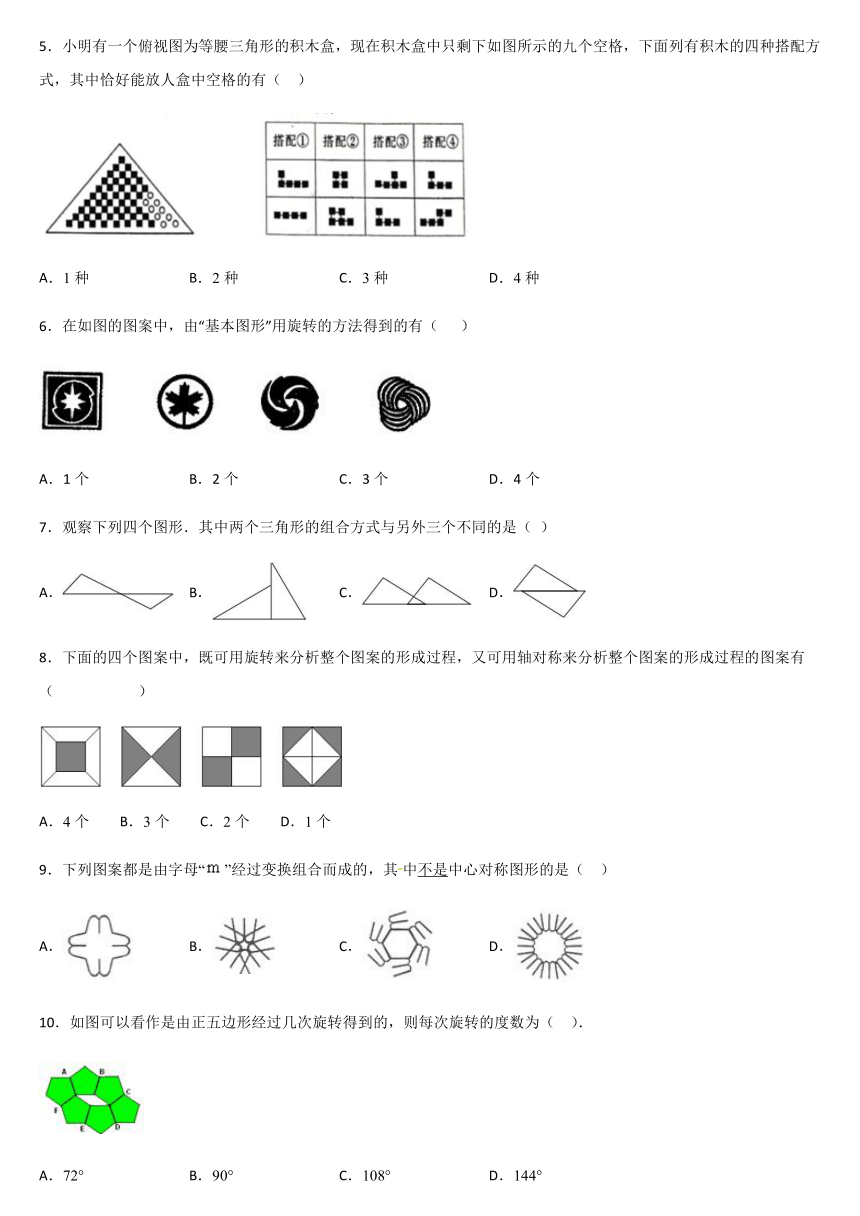
1.如图①是3×3正方形方格,将其中两个方格涂黑,并且使得涂黑后的整个图案是轴对称图形,约定绕正方形ABCD的中心旋转能重合的图案都视为同一种,例②中四幅图就视为同一种,则得到不同共有(
)
A.4种
B.5种
C.6种
D.7种
2.如图,在小正三角形组成的网格中,已有个小正三角形涂黑,还需涂黑个小正三角形,使它们与原来涂黑的小正三角形组成的新图案恰有三条对称轴,则的最小值为( )
A.
B.
C.
D.
3.风车应做成中心对称图形,并且不是轴对称图形,才能在风口处平稳旋转.现有一长条矩形硬纸板(其中心有一个小孔)和两张全等的矩形薄纸片,将纸片黏到硬纸板上,做成一个能绕着小孔平稳旋转的风车.正确的黏合方法是
(
)
A.
B.
C.
D.
4.下列图形可以由一个图形经过平移变换得到的是(
)
5.小明有一个俯视图为等腰三角形的积木盒,现在积木盒中只剩下如图所示的九个空格,下面列有积木的四种搭配方式,其中恰好能放人盒中空格的有(
)
A.1种
B.2种
C.3种
D.4种
6.在如图的图案中,由“基本图形”用旋转的方法得到的有(????
)
A.1个
B.2个
C.3个
D.4个
7.观察下列四个图形.其中两个三角形的组合方式与另外三个不同的是(
)
A.
B.
C.
D.
8.下面的四个图案中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有(
)
A.4个
B.3个
C.2个
D.1个
9.下列图案都是由字母“”经过变换组合而成的,其中不是中心对称图形的是( )
A.
B.
C.
D.
10.如图可以看作是由正五边形经过几次旋转得到的,则每次旋转的度数为(??
).
A.72°
B.90°
C.108°
D.144°
二、填空题
11.如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转_____次,每次旋转_____度形成的.
12.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有__________种.
13.如图,请画出一个图形经过两次轴对称变换之后得到的图形,其中图①中的两条对称轴是平行的,图②中的两条对称轴是垂直的.仔细观察上面的两个图形经过两次轴对称变换之后得到的图形.图①中的图形除经过两次轴对称变换得到之外,还可以通过我们学过的________变换得到,图②中的图形还可以通过________变换得到.
14.如图,甲图怎样变成乙图:________.
15.若抛物线y=ax2+c与x轴交于点A(m,0),B(n,0),与y轴交于点C(0,c),则称△ABC为“抛物三角形”.特别地,当mnc<0时,称△ABC为“正抛物三角形”;当mnc>0时,称△ABC为“倒抛物三角形”.若△ABC为“倒抛物三角形”时,a、c应分别满足条件_____、_____;若△ABC为“正抛物三角形”,此时△ABC及其关于x轴的轴对称图形恰好构成了一个含60°角的菱形,则a、c应满足的关系为_____.
三、解答题
16.已知每个网格中小正方形的边长都是1,图①中的阴影图案是由三段以格点为圆心,半径分别为1和2的圆弧围成的.请你在图②中以图①为基本图案,借助平移或旋转设计一个完整的花边图案.
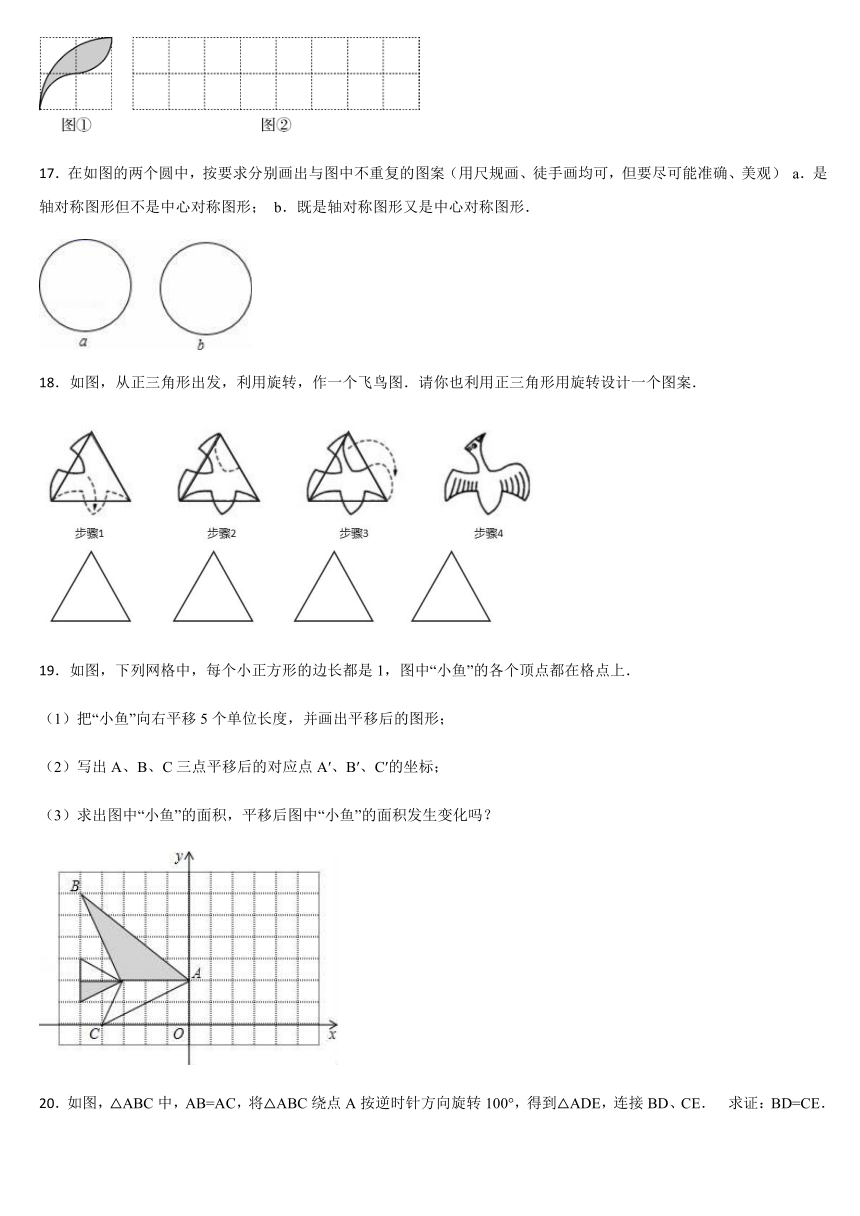
17.在如图的两个圆中,按要求分别画出与图中不重复的图案(用尺规画、徒手画均可,但要尽可能准确、美观)
a.是轴对称图形但不是中心对称图形;
b.既是轴对称图形又是中心对称图形.
18.如图,从正三角形出发,利用旋转,作一个飞鸟图.请你也利用正三角形用旋转设计一个图案.
19.如图,下列网格中,每个小正方形的边长都是1,图中“小鱼”的各个顶点都在格点上.
(1)把“小鱼”向右平移5个单位长度,并画出平移后的图形;
(2)写出A、B、C三点平移后的对应点A′、B′、C′的坐标;
(3)求出图中“小鱼”的面积,平移后图中“小鱼”的面积发生变化吗?
20.如图,△ABC中,AB=AC,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD、CE.
求证:BD=CE.
21.如图,在平行四边形中挖去一个矩形,在请用无刻度的直尺,准确作出一条直线,将剩下图形的面积平分.(保留作图痕迹)?
22.规定:在平面内,如果一个图形绕一个定点旋转一定的角度α(0°<α≤180°)后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角度α称为这个图形的一个旋转角.例如:正方形绕着两条对角线的交点O旋转90°或180°后,能与自身重合(如图1),所以正方形是旋转对称图形,且有两个旋转角.根据以上规定,回答问题:
(1)下列图形是旋转对称图形,但不是中心对称图形的是________;
A.矩形
B.正五边形
C.菱形
D.正六边形
(2)下列图形中,是旋转对称图形,且有一个旋转角是60度的有:________(填序号);
(3)下列三个命题:①中心对称图形是旋转对称图形;②等腰三角形是旋转对称图形;③圆是旋转对称图形,其中真命题的个数有(
)个;
A.0
B.1
C.2
D.3
(4)如图2的旋转对称图形由等腰直角三角形和圆构成,旋转角有45°,90°,135°,180°,将图形补充完整.
23.在数学活动课上,王老师要求学生将图1所示的3×3正方形方格纸,剪掉其中两个方格,使之成为轴对称图形.规定:凡通过旋转能重合的图形视为同一种图形,如图2的四幅图就视为同一种设计方案(阴影部分为要剪掉部分)
请在图中画出4种不同的设计方案,将每种方案中要剪掉的两个方格涂黑(每个3×3的正方形方格画一种,例图除外)
【参考答案】
1.B
2.C
3.A
4.B
5.D
6.C
7.C
8.A
9.B
10.C
11.7
45
12.C
13.平移
旋转
14.先将甲逆时针旋转度,再向左平移,就能与乙图重合.
15.a>0,
c<0
ac=﹣3或﹣.
16.答案不唯一,由图1进行平移和旋转即可.
17如图所示:
18.如图所示:
19解:(1)如图所示:
.
(2)结合坐标系可得:A'(5,2),B'(0,6),C'(1,0);
(3)图中“小鱼”的面积=×3×4+2×2+3×2=11,
∵平移只改变图形的位置,图形的大小,形状不变,
∴平移后图中“小鱼”的面积发生变化.
20.证明:∵△ABC绕点A按逆时针方向旋转100°得△ADE,
∴∠BAD=∠CAE=100°.
又∵AB=AC,
∴AB=AC=AD=AE.?
在△ABD与△ACE中,
∵
,
∴△ABD≌△ACE(SAS).
∴BD=CE.
21.如图所示:
22.解:(1)矩形、正五边形、菱形、正六边形都是旋转对称图形,但正五边形不是中心对称图形,
故选:B.
(2)是旋转对称图形,且有一个旋转角是60度的有(1)(3)(5).
故答案为:(1)(3)(5).
(3)①中心对称图形,旋转180°一定会和本身重合,是旋转对称图形;故命题①正确;
②等腰三角形绕一个定点旋转一定的角度α(0°<α≤180°)后,不一定能与自身重合,只有等边三角形是旋转对称图形,故②不正确;
③圆具有旋转不变性,绕圆心旋转任意角度一定能与自身重合,是旋转对称图形;故命题③正确;
即命题中①③正确,
故选:C.
(4)图形如图所示:
23.解:根据剪掉其中两个方格,使之成为轴对称图形;即如图所示:
第二十三章
旋转
23.3
课题学习
图案设计
课后练习
一、选择题
1.如图①是3×3正方形方格,将其中两个方格涂黑,并且使得涂黑后的整个图案是轴对称图形,约定绕正方形ABCD的中心旋转能重合的图案都视为同一种,例②中四幅图就视为同一种,则得到不同共有(
)
A.4种
B.5种
C.6种
D.7种
2.如图,在小正三角形组成的网格中,已有个小正三角形涂黑,还需涂黑个小正三角形,使它们与原来涂黑的小正三角形组成的新图案恰有三条对称轴,则的最小值为( )
A.
B.
C.
D.
3.风车应做成中心对称图形,并且不是轴对称图形,才能在风口处平稳旋转.现有一长条矩形硬纸板(其中心有一个小孔)和两张全等的矩形薄纸片,将纸片黏到硬纸板上,做成一个能绕着小孔平稳旋转的风车.正确的黏合方法是
(
)
A.
B.
C.
D.
4.下列图形可以由一个图形经过平移变换得到的是(
)
5.小明有一个俯视图为等腰三角形的积木盒,现在积木盒中只剩下如图所示的九个空格,下面列有积木的四种搭配方式,其中恰好能放人盒中空格的有(
)
A.1种
B.2种
C.3种
D.4种
6.在如图的图案中,由“基本图形”用旋转的方法得到的有(????
)
A.1个
B.2个
C.3个
D.4个
7.观察下列四个图形.其中两个三角形的组合方式与另外三个不同的是(
)
A.
B.
C.
D.
8.下面的四个图案中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有(
)
A.4个
B.3个
C.2个
D.1个
9.下列图案都是由字母“”经过变换组合而成的,其中不是中心对称图形的是( )
A.
B.
C.
D.
10.如图可以看作是由正五边形经过几次旋转得到的,则每次旋转的度数为(??
).
A.72°
B.90°
C.108°
D.144°
二、填空题
11.如图所示的美丽图案,可以看作是由一个三角形绕旋转中心旋转_____次,每次旋转_____度形成的.
12.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有__________种.
13.如图,请画出一个图形经过两次轴对称变换之后得到的图形,其中图①中的两条对称轴是平行的,图②中的两条对称轴是垂直的.仔细观察上面的两个图形经过两次轴对称变换之后得到的图形.图①中的图形除经过两次轴对称变换得到之外,还可以通过我们学过的________变换得到,图②中的图形还可以通过________变换得到.
14.如图,甲图怎样变成乙图:________.
15.若抛物线y=ax2+c与x轴交于点A(m,0),B(n,0),与y轴交于点C(0,c),则称△ABC为“抛物三角形”.特别地,当mnc<0时,称△ABC为“正抛物三角形”;当mnc>0时,称△ABC为“倒抛物三角形”.若△ABC为“倒抛物三角形”时,a、c应分别满足条件_____、_____;若△ABC为“正抛物三角形”,此时△ABC及其关于x轴的轴对称图形恰好构成了一个含60°角的菱形,则a、c应满足的关系为_____.
三、解答题
16.已知每个网格中小正方形的边长都是1,图①中的阴影图案是由三段以格点为圆心,半径分别为1和2的圆弧围成的.请你在图②中以图①为基本图案,借助平移或旋转设计一个完整的花边图案.
17.在如图的两个圆中,按要求分别画出与图中不重复的图案(用尺规画、徒手画均可,但要尽可能准确、美观)
a.是轴对称图形但不是中心对称图形;
b.既是轴对称图形又是中心对称图形.
18.如图,从正三角形出发,利用旋转,作一个飞鸟图.请你也利用正三角形用旋转设计一个图案.
19.如图,下列网格中,每个小正方形的边长都是1,图中“小鱼”的各个顶点都在格点上.
(1)把“小鱼”向右平移5个单位长度,并画出平移后的图形;
(2)写出A、B、C三点平移后的对应点A′、B′、C′的坐标;
(3)求出图中“小鱼”的面积,平移后图中“小鱼”的面积发生变化吗?
20.如图,△ABC中,AB=AC,将△ABC绕点A按逆时针方向旋转100°,得到△ADE,连接BD、CE.
求证:BD=CE.
21.如图,在平行四边形中挖去一个矩形,在请用无刻度的直尺,准确作出一条直线,将剩下图形的面积平分.(保留作图痕迹)?
22.规定:在平面内,如果一个图形绕一个定点旋转一定的角度α(0°<α≤180°)后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角度α称为这个图形的一个旋转角.例如:正方形绕着两条对角线的交点O旋转90°或180°后,能与自身重合(如图1),所以正方形是旋转对称图形,且有两个旋转角.根据以上规定,回答问题:
(1)下列图形是旋转对称图形,但不是中心对称图形的是________;
A.矩形
B.正五边形
C.菱形
D.正六边形
(2)下列图形中,是旋转对称图形,且有一个旋转角是60度的有:________(填序号);
(3)下列三个命题:①中心对称图形是旋转对称图形;②等腰三角形是旋转对称图形;③圆是旋转对称图形,其中真命题的个数有(
)个;
A.0
B.1
C.2
D.3
(4)如图2的旋转对称图形由等腰直角三角形和圆构成,旋转角有45°,90°,135°,180°,将图形补充完整.
23.在数学活动课上,王老师要求学生将图1所示的3×3正方形方格纸,剪掉其中两个方格,使之成为轴对称图形.规定:凡通过旋转能重合的图形视为同一种图形,如图2的四幅图就视为同一种设计方案(阴影部分为要剪掉部分)
请在图中画出4种不同的设计方案,将每种方案中要剪掉的两个方格涂黑(每个3×3的正方形方格画一种,例图除外)
【参考答案】
1.B
2.C
3.A
4.B
5.D
6.C
7.C
8.A
9.B
10.C
11.7
45
12.C
13.平移
旋转
14.先将甲逆时针旋转度,再向左平移,就能与乙图重合.
15.a>0,
c<0
ac=﹣3或﹣.
16.答案不唯一,由图1进行平移和旋转即可.
17如图所示:
18.如图所示:
19解:(1)如图所示:
.
(2)结合坐标系可得:A'(5,2),B'(0,6),C'(1,0);
(3)图中“小鱼”的面积=×3×4+2×2+3×2=11,
∵平移只改变图形的位置,图形的大小,形状不变,
∴平移后图中“小鱼”的面积发生变化.
20.证明:∵△ABC绕点A按逆时针方向旋转100°得△ADE,
∴∠BAD=∠CAE=100°.
又∵AB=AC,
∴AB=AC=AD=AE.?
在△ABD与△ACE中,
∵
,
∴△ABD≌△ACE(SAS).
∴BD=CE.
21.如图所示:
22.解:(1)矩形、正五边形、菱形、正六边形都是旋转对称图形,但正五边形不是中心对称图形,
故选:B.
(2)是旋转对称图形,且有一个旋转角是60度的有(1)(3)(5).
故答案为:(1)(3)(5).
(3)①中心对称图形,旋转180°一定会和本身重合,是旋转对称图形;故命题①正确;
②等腰三角形绕一个定点旋转一定的角度α(0°<α≤180°)后,不一定能与自身重合,只有等边三角形是旋转对称图形,故②不正确;
③圆具有旋转不变性,绕圆心旋转任意角度一定能与自身重合,是旋转对称图形;故命题③正确;
即命题中①③正确,
故选:C.
(4)图形如图所示:
23.解:根据剪掉其中两个方格,使之成为轴对称图形;即如图所示:
同课章节目录
