人教版七年级上册4.3.2 角的比较与运算 课件(共29张)
文档属性
| 名称 | 人教版七年级上册4.3.2 角的比较与运算 课件(共29张) |

|
|
| 格式 | zip | ||
| 文件大小 | 926.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-20 00:00:00 | ||
图片预览






文档简介
(共29张PPT)
4.3.2
角的比较与运算
第四章
图形初步认识
4.3
角
学习目标
1.
掌握角的大小的比较方法.
(重点)
2.
理解角平分线和角的和、差、倍、分的意义及数量关系,能够用几何语言进行相关表述,并能解答相关问题.
(重点、难点)
3.
会进行涉及度、分、秒的角度的计算.
(重点、难点)
A
B
C
D
E
F
怎样比较∠ABC和∠DEF的大小?
1.
如图,已知线段AB、CD,你有哪些办法比较它们的大小?
温故知新,引入新课
2.叠合法
1.度量法
3.尺规作图
讲授新课
角的比较与计算
一
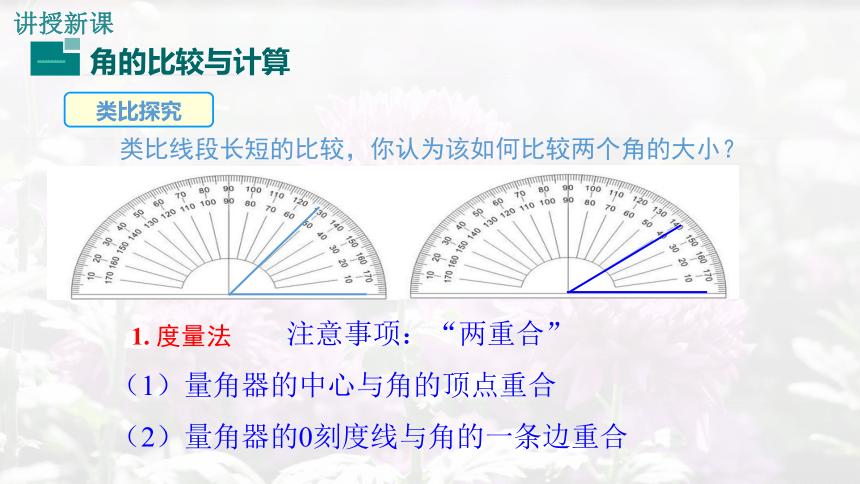
类比线段长短的比较,你认为该如何比较两个角的大小?
1.
度量法
类比探究
注意事项:“两重合”
(1)量角器的中心与角的顶点重合
(2)量角器的0刻度线与角的一条边重合
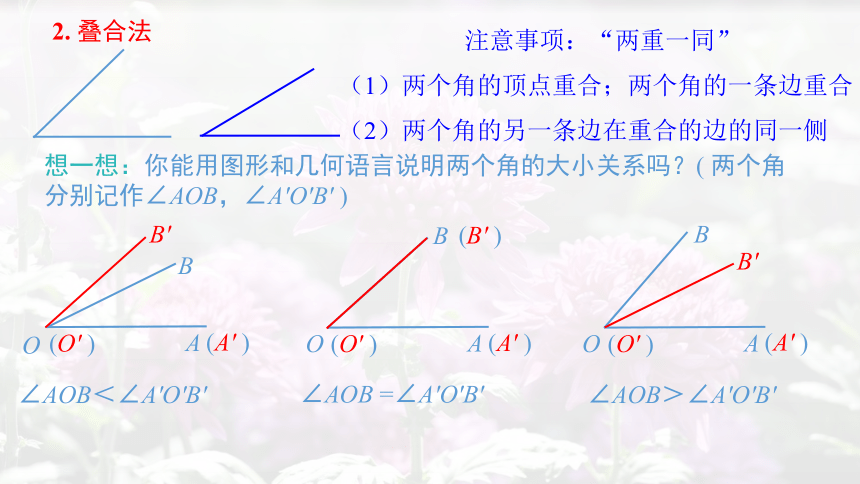
2.
叠合法
A
B
O
(O'
)
B'
(A'
)
A
B
O
A
B
O
想一想:你能用图形和几何语言说明两个角的大小关系吗?(
两个角分别记作∠AOB,∠A'O'B'
)
(O'
)
B'
(A'
)
∠AOB<∠A'O'B'
∠AOB
=∠A'O'B'
∠AOB>∠A'O'B'
(O'
)
(B'
)
(A'
)
注意事项:“两重一同”
(1)两个角的顶点重合;两个角的一条边重合
(2)两个角的另一条边在重合的边的同一侧
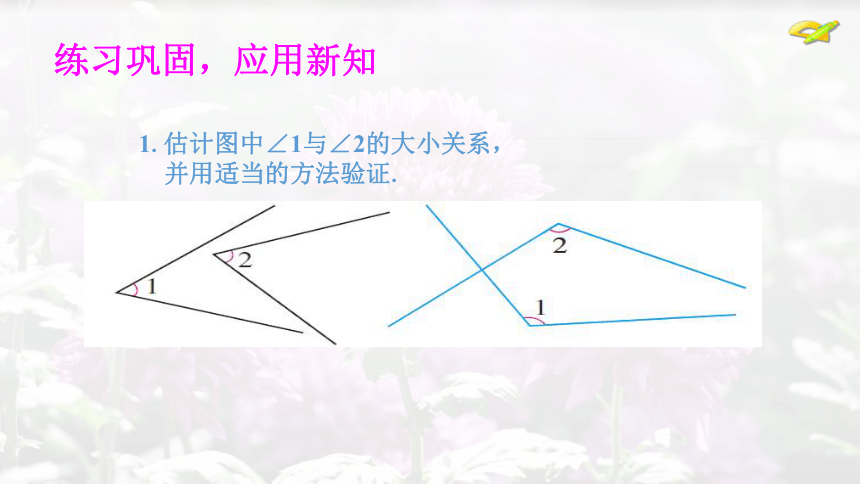
1.估计图中∠1与∠2的大小关系,
并用适当的方法验证.
练习巩固,应用新知
图中有几个角?它们之间有什么关系?
图中有3个角:∠AOC,∠AOB,∠BOC.
∠AOC
是∠AOB
与∠BOC的和,记作∠AOC
=
∠AOB
+∠BOC;
它们的关系:
∠AOB
是∠AOC与∠BOC的差,记作∠AOB
=
∠AOC-∠BOC;
类似地,∠AOC-∠AOB=
.
∠BOC
A
B
O
C
思考
按图1填空:
4)∠A0B+∠BOC=
5)∠A0C+∠COD=
6)∠B0D-∠COD=
7)∠A0D-
=∠A0B
O
D
C
B
A
图1
∠AOC
∠AOD
∠BOC
∠BOD
1)
∠D0B
∠BOC
2)
∠C0B
∠AOC
3)
∠DOC+∠COB
∠B0D
>
<
=
同类练习:
如图,借助一副三角尺可以画出15°和75°的角,你还能画出哪些度数的角?
探究1:
75°
15°
105°、120°、135°、150°、165
°180°
C
A
O
B
动手做一做:在纸上画∠AOC,然后将其剪下来,将其沿经过顶点的线对折,使边OA与OC重合.将角展开,折痕上任取一点记作点B.类比线段中点的定义,填空:
∠AOB=∠BOC=
;
∠AOC=2∠AOB=2__
___.
观察思考,探究新知
1
2
∠AOC
∠BOC
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
应用格式:
因为
OB
是∠AOC
的角平分线,
所以∠AOB
=∠BOC
=
∠AOC,
∠AOC=2∠BOC
=2∠AOB.
O
C
A
B
A
B
C
D
O
如图
∠AOB=∠BOC=∠COD,
则OB
是
的平分线,
= ∠AOC,
= ∠BOD
∠BOC
=
=
AOC
BOC
BOC
AOD
BOD
此时OB、OC叫∠
AOD的三等分线
跟踪练习
AOD
探究2
如何作一个角的平分线?你能想到什么方法?
度量法
折纸法
达标检测
1.在小于平角的∠AOB的内部取一点C,并作射线OC,则一定存在(
).
(A)∠AOC>∠BOC
(B)∠AOC=∠BOC
(C)∠AOB>∠AOC
(D)∠BOC>∠AOC
2.
射线OC在∠AOB的内部,下列四个式子中不能判定OC是∠AOB的平分线的是(
).
(A)∠AOB=2∠AOC
(B)∠BOC=∠AOC
(C)2∠AOC=∠AOB (D)∠AOC+∠BOC=∠AOB
3.OC是∠AOB内部的一条射线,若∠AOC=
_____,则OC平分∠AOB;若OC
是∠AOB的角平分线,则_________=2∠AOC.
C
D
4.
如图(2),用“=”或“>”或“<”填空:
(1)∠AOC_______∠AOB+∠BOC;
(2)∠AOC_______∠AOB;
(3)∠BOD-∠BOC______∠DOC;
(4)∠AOD______∠AOC+∠BOD.
5.如图(3),OC平分∠AOB,OD平分∠AOC,则图中相等的角有___
_____,∠AOD=______∠AOC=______∠AOB
6.
如图所示,已知∠COD==25°,∠AOC=∠BOD=90°,则∠AOD=______,∠AOB=______
第6题
=
>
=
<
1/2
1/4
65°
155°
例1
如图,O
是直线
AB
上一点,∠AOC=53°17′,
求∠BOC
的度数.
解:因为∠AOB
是平角,
∠AOB=
∠AOC+∠BOC.
所以∠BOC=∠AOB-∠AOC
=180°-53°17′
=179°60′-53°17′
=126°43′.
O
C
B
A
如何计算?
可以向
180?
借
1?,化为60′.
例2
把一个周角
7
等分,每一份是多少度的角
(精确到分)?
解:360°÷7
=
51°+3°÷7
=
51°+180′÷7
≈
51°26′.
答:每份是51°26′的角.
有余数,可以把度的余数化成分后再除
(1)67°31′+48°49′.
解:原式
=
(67+48)°+(31+49)′
=
115°97′
=
116°37′
.
计算
(2)
21°17′×5;
解:原式
=
21°×5+17′×5
=
105°85′
=
106°25
′
涉及到度、分、秒的角度的加与减,要将度与度、分与分、秒与秒分别相加、减,分秒相加时逢60要进位,相减时要借1作60.
1.计算:
34°34′+21°51′=
变式训练一:
2.计算:180°-52°31′=
在进行加法运算时,度和度加,分和分加,秒和秒加,若所得的分或秒等于或大于60,则进一位;在进行减法运算时,度和度减,分和分减,秒和秒减,若度或分小于60,则借一位.
在进行乘除运算时,角的度数的每一部分分别相乘或相除,还要注意最后的结果中若分或秒大于或等于60,则进一位.
变式训练二:
2.
如图,OC是平角∠AOB的角平分线,∠COD=31°28′,
求∠BOD的度数.
答案:∠BOD=58°32′.
O
A
B
C
D
如图,OB
是∠AOC
的平分线,OD
是∠COE的平分线.
(1)
如果∠AOC=80°,那么∠BOC
是多少度?
解:因为
OB
平分∠AOC,∠AOC=80°,
O
A
B
C
D
E
所以∠BOC=
∠AOC
=
×80°=40°.
巩固练习:
(2)
如果∠AOB=40°,∠DOE=30°,那么∠BOD
是多少度?
解:因为
OB
平分∠AOC,
所以
∠BOC=∠AOB
=
40°.
因为
OD
平分∠COE,
所以∠COD=∠DOE
=
30°,
所以∠BOD
=∠BOC+∠COD
=
40°+30°=
70°.
O
A
B
C
D
E
(3)
如果∠AOE=140°,
∠COD=30°,那么∠AOB
是多少度?
解:因为
∠COD=30°,
OD
平分∠COE,
所以
∠COE=2∠COD=60°,
所以
∠AOC=∠AOE-∠COE
=140°-60°=
80°.
又因为
OB
平分∠AOC,
O
A
B
C
D
E
所以∠AOB=
∠AOC=
×80°=
40°.
角的比较
角的平分线
度量法
叠合法
角的运算
加与减
乘与除
角的和差倍分关系
角的计算
小结与回顾
今天你学到了哪些知识?
达标检测
1.度分秒的计算,并总结计算方法,与你的同伴交流。
⑴
57.32?= 度
分
秒,
⑵
17°6′36″=
度,
⑶
14°25′12″=
度,
⑷
28°39′+
61°35′=___________
,
⑸
54°23′-
36°31′=____________
,
⑹
23°32′×3=___________。
2.如图,OC是∠AOB的平分线,OD平分∠AOC,且∠COD=25°,则∠AOB=(
).
(A)100°
(B)75° (C)50°
(D)20°
57
19
12
17.11
14.42
90°14′
17°52′
70°34′
A
3、如图,∠BAD=____+_____;∠CAE=_____+_____
如果∠BAD=∠CAE,那么图中有相等的两角
是:______=______.
4.已知∠AOB=38°,∠BOC=25°,
那么∠AOC的度数是___ ___
?
5.如图,OC是平角∠AOB的角平分线,∠COD=32°,
求∠AOD的度数。
D
C
O
B
A
63°或 13°
122°
6.如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC=___.
7.如图,AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°,求∠AOC的度数?
O
C
A
D
B
O
C
A
E
D
B
34°
30°
4.3.2
角的比较与运算
第四章
图形初步认识
4.3
角
学习目标
1.
掌握角的大小的比较方法.
(重点)
2.
理解角平分线和角的和、差、倍、分的意义及数量关系,能够用几何语言进行相关表述,并能解答相关问题.
(重点、难点)
3.
会进行涉及度、分、秒的角度的计算.
(重点、难点)
A
B
C
D
E
F
怎样比较∠ABC和∠DEF的大小?
1.
如图,已知线段AB、CD,你有哪些办法比较它们的大小?
温故知新,引入新课
2.叠合法
1.度量法
3.尺规作图
讲授新课
角的比较与计算
一
类比线段长短的比较,你认为该如何比较两个角的大小?
1.
度量法
类比探究
注意事项:“两重合”
(1)量角器的中心与角的顶点重合
(2)量角器的0刻度线与角的一条边重合
2.
叠合法
A
B
O
(O'
)
B'
(A'
)
A
B
O
A
B
O
想一想:你能用图形和几何语言说明两个角的大小关系吗?(
两个角分别记作∠AOB,∠A'O'B'
)
(O'
)
B'
(A'
)
∠AOB<∠A'O'B'
∠AOB
=∠A'O'B'
∠AOB>∠A'O'B'
(O'
)
(B'
)
(A'
)
注意事项:“两重一同”
(1)两个角的顶点重合;两个角的一条边重合
(2)两个角的另一条边在重合的边的同一侧
1.估计图中∠1与∠2的大小关系,
并用适当的方法验证.
练习巩固,应用新知
图中有几个角?它们之间有什么关系?
图中有3个角:∠AOC,∠AOB,∠BOC.
∠AOC
是∠AOB
与∠BOC的和,记作∠AOC
=
∠AOB
+∠BOC;
它们的关系:
∠AOB
是∠AOC与∠BOC的差,记作∠AOB
=
∠AOC-∠BOC;
类似地,∠AOC-∠AOB=
.
∠BOC
A
B
O
C
思考
按图1填空:
4)∠A0B+∠BOC=
5)∠A0C+∠COD=
6)∠B0D-∠COD=
7)∠A0D-
=∠A0B
O
D
C
B
A
图1
∠AOC
∠AOD
∠BOC
∠BOD
1)
∠D0B
∠BOC
2)
∠C0B
∠AOC
3)
∠DOC+∠COB
∠B0D
>
<
=
同类练习:
如图,借助一副三角尺可以画出15°和75°的角,你还能画出哪些度数的角?
探究1:
75°
15°
105°、120°、135°、150°、165
°180°
C
A
O
B
动手做一做:在纸上画∠AOC,然后将其剪下来,将其沿经过顶点的线对折,使边OA与OC重合.将角展开,折痕上任取一点记作点B.类比线段中点的定义,填空:
∠AOB=∠BOC=
;
∠AOC=2∠AOB=2__
___.
观察思考,探究新知
1
2
∠AOC
∠BOC
一般地,从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
应用格式:
因为
OB
是∠AOC
的角平分线,
所以∠AOB
=∠BOC
=
∠AOC,
∠AOC=2∠BOC
=2∠AOB.
O
C
A
B
A
B
C
D
O
如图
∠AOB=∠BOC=∠COD,
则OB
是
的平分线,
= ∠AOC,
= ∠BOD
∠BOC
=
=
AOC
BOC
BOC
AOD
BOD
此时OB、OC叫∠
AOD的三等分线
跟踪练习
AOD
探究2
如何作一个角的平分线?你能想到什么方法?
度量法
折纸法
达标检测
1.在小于平角的∠AOB的内部取一点C,并作射线OC,则一定存在(
).
(A)∠AOC>∠BOC
(B)∠AOC=∠BOC
(C)∠AOB>∠AOC
(D)∠BOC>∠AOC
2.
射线OC在∠AOB的内部,下列四个式子中不能判定OC是∠AOB的平分线的是(
).
(A)∠AOB=2∠AOC
(B)∠BOC=∠AOC
(C)2∠AOC=∠AOB (D)∠AOC+∠BOC=∠AOB
3.OC是∠AOB内部的一条射线,若∠AOC=
_____,则OC平分∠AOB;若OC
是∠AOB的角平分线,则_________=2∠AOC.
C
D
4.
如图(2),用“=”或“>”或“<”填空:
(1)∠AOC_______∠AOB+∠BOC;
(2)∠AOC_______∠AOB;
(3)∠BOD-∠BOC______∠DOC;
(4)∠AOD______∠AOC+∠BOD.
5.如图(3),OC平分∠AOB,OD平分∠AOC,则图中相等的角有___
_____,∠AOD=______∠AOC=______∠AOB
6.
如图所示,已知∠COD==25°,∠AOC=∠BOD=90°,则∠AOD=______,∠AOB=______
第6题
=
>
=
<
1/2
1/4
65°
155°
例1
如图,O
是直线
AB
上一点,∠AOC=53°17′,
求∠BOC
的度数.
解:因为∠AOB
是平角,
∠AOB=
∠AOC+∠BOC.
所以∠BOC=∠AOB-∠AOC
=180°-53°17′
=179°60′-53°17′
=126°43′.
O
C
B
A
如何计算?
可以向
180?
借
1?,化为60′.
例2
把一个周角
7
等分,每一份是多少度的角
(精确到分)?
解:360°÷7
=
51°+3°÷7
=
51°+180′÷7
≈
51°26′.
答:每份是51°26′的角.
有余数,可以把度的余数化成分后再除
(1)67°31′+48°49′.
解:原式
=
(67+48)°+(31+49)′
=
115°97′
=
116°37′
.
计算
(2)
21°17′×5;
解:原式
=
21°×5+17′×5
=
105°85′
=
106°25
′
涉及到度、分、秒的角度的加与减,要将度与度、分与分、秒与秒分别相加、减,分秒相加时逢60要进位,相减时要借1作60.
1.计算:
34°34′+21°51′=
变式训练一:
2.计算:180°-52°31′=
在进行加法运算时,度和度加,分和分加,秒和秒加,若所得的分或秒等于或大于60,则进一位;在进行减法运算时,度和度减,分和分减,秒和秒减,若度或分小于60,则借一位.
在进行乘除运算时,角的度数的每一部分分别相乘或相除,还要注意最后的结果中若分或秒大于或等于60,则进一位.
变式训练二:
2.
如图,OC是平角∠AOB的角平分线,∠COD=31°28′,
求∠BOD的度数.
答案:∠BOD=58°32′.
O
A
B
C
D
如图,OB
是∠AOC
的平分线,OD
是∠COE的平分线.
(1)
如果∠AOC=80°,那么∠BOC
是多少度?
解:因为
OB
平分∠AOC,∠AOC=80°,
O
A
B
C
D
E
所以∠BOC=
∠AOC
=
×80°=40°.
巩固练习:
(2)
如果∠AOB=40°,∠DOE=30°,那么∠BOD
是多少度?
解:因为
OB
平分∠AOC,
所以
∠BOC=∠AOB
=
40°.
因为
OD
平分∠COE,
所以∠COD=∠DOE
=
30°,
所以∠BOD
=∠BOC+∠COD
=
40°+30°=
70°.
O
A
B
C
D
E
(3)
如果∠AOE=140°,
∠COD=30°,那么∠AOB
是多少度?
解:因为
∠COD=30°,
OD
平分∠COE,
所以
∠COE=2∠COD=60°,
所以
∠AOC=∠AOE-∠COE
=140°-60°=
80°.
又因为
OB
平分∠AOC,
O
A
B
C
D
E
所以∠AOB=
∠AOC=
×80°=
40°.
角的比较
角的平分线
度量法
叠合法
角的运算
加与减
乘与除
角的和差倍分关系
角的计算
小结与回顾
今天你学到了哪些知识?
达标检测
1.度分秒的计算,并总结计算方法,与你的同伴交流。
⑴
57.32?= 度
分
秒,
⑵
17°6′36″=
度,
⑶
14°25′12″=
度,
⑷
28°39′+
61°35′=___________
,
⑸
54°23′-
36°31′=____________
,
⑹
23°32′×3=___________。
2.如图,OC是∠AOB的平分线,OD平分∠AOC,且∠COD=25°,则∠AOB=(
).
(A)100°
(B)75° (C)50°
(D)20°
57
19
12
17.11
14.42
90°14′
17°52′
70°34′
A
3、如图,∠BAD=____+_____;∠CAE=_____+_____
如果∠BAD=∠CAE,那么图中有相等的两角
是:______=______.
4.已知∠AOB=38°,∠BOC=25°,
那么∠AOC的度数是___ ___
?
5.如图,OC是平角∠AOB的角平分线,∠COD=32°,
求∠AOD的度数。
D
C
O
B
A
63°或 13°
122°
6.如图,∠AOB=∠COD=90°,∠AOD=146°,则∠BOC=___.
7.如图,AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°,求∠AOC的度数?
O
C
A
D
B
O
C
A
E
D
B
34°
30°
