人教版九年级数学下册练习题:26.2实际问题与反比例函数(word版,含答案)
文档属性
| 名称 | 人教版九年级数学下册练习题:26.2实际问题与反比例函数(word版,含答案) | 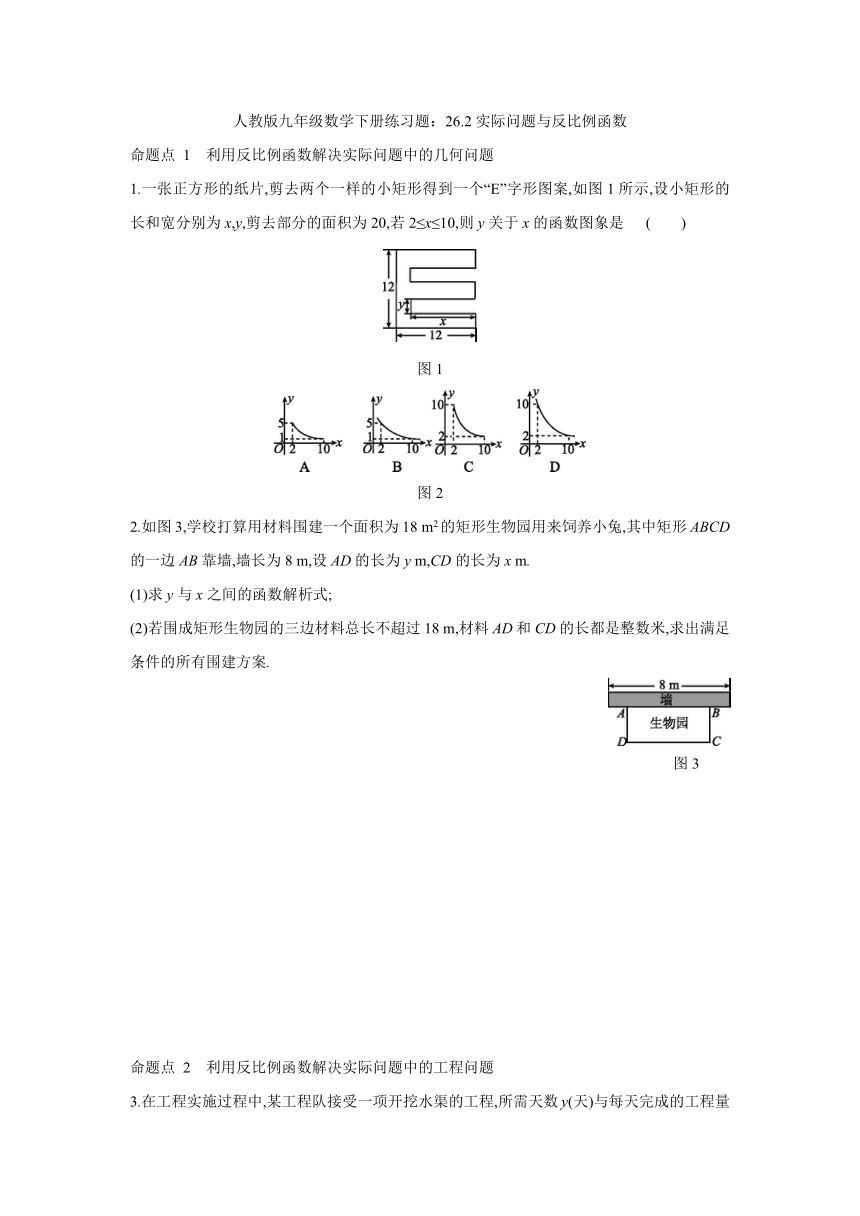 | |
| 格式 | zip | ||
| 文件大小 | 421.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-20 07:24:34 | ||
图片预览





文档简介
人教版九年级数学下册练习题:26.2实际问题与反比例函数
命题点
1 利用反比例函数解决实际问题中的几何问题
1.一张正方形的纸片,剪去两个一样的小矩形得到一个“E”字形图案,如图1所示,设小矩形的长和宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y关于x的函数图象是
( )
图1
图2
2.如图3,学校打算用材料围建一个面积为18
m2的矩形生物园用来饲养小兔,其中矩形ABCD的一边AB靠墙,墙长为8
m,设AD的长为y
m,CD的长为x
m.
(1)求y与x之间的函数解析式;
(2)若围成矩形生物园的三边材料总长不超过18
m,材料AD和CD的长都是整数米,求出满足条件的所有围建方案.
图3
命题点
2 利用反比例函数解决实际问题中的工程问题
3.在工程实施过程中,某工程队接受一项开挖水渠的工程,所需天数y(天)与每天完成的工程量x(米)的函数关系图象如图4所示,是双曲线的一部分.
(1)请根据题意,求y与x之间的函数解析式;
(2)若该工程队有2台挖掘机,每台挖掘机每天能够开挖水渠30米,则该工程队需要用多少天才能完成此项任务?
(3)如果为了防汛工作的紧急需要,必须在10天内完成任务,那么该工程队每天至少要完成多少米?
图4
命题点
3 利用反比例函数解决实际问题中的商品销售问题
4.李老师参加了某电脑公司推出的分期付款购买电脑活动(无利息),他购买的电脑价格为9800元,交了首付之后每月付款y元,x个月结清贷款,y与x满足如图5所示的函数关系,通过以上信息可知李老师的首付款为 元.?
图5
5.水果店在销售某种水果,该种水果的进价为10元/kg.根据以往的销售经验可知:日销量y(单位:kg)随售价x(单位:元/kg)的变化规律符合某种函数关系.
该水果店以往的销售记录如下表:(售价不低于进价)
售价x(单位:元/kg)
10
15
20
25
30
日销量y(单位:kg)
30
20
15
12
10
若y与x之间的函数关系是一次函数、二次函数、反比例函数中的某一种.
(1)判断y与x之间的函数关系,并写出其解析式;
(2)水果店销售该种水果的日利润能否达到200元?说明理由.
命题点
4 利用反比例函数解决实际问题中的行程问题
6.一辆汽车通过某段公路时,行驶时间t(h)与行驶速度v(km/h)满足反比例函数关系t=,其图象为一段曲线(如图6),端点为A(35,1.2),B(m,0.5).
(1)求k和m的值;
(2)若该路段限速60
km/h,则汽车通过该路段至少需要多少时间?
图6
7.超越公司将某品牌农副产品运往新时代市场进行销售,记汽车的行驶时间为t(时),平均速度为v(千米/时)(汽车行驶速度不超过100千米/时).根据经验,v,t的几组对应值如下表:
v(千米/时)
75
80
85
90
95
t(时)
4.00
3.75
3.53
3.33
3.16
(1)根据表中的数据,求出平均速度v(千米/时)关于行驶时间t(时)的函数解析式;
(2)汽车上午7:30从超越公司出发,能否在上午10:00之前到达新时代市场?说明理由.
命题点
5 反比例函数和一次函数在实际问题中的综合应用
8.[2019·成都金牛区月考]
小成利用暑期参加社会实践活动,在妈妈的帮助下,利用社区提供的免费摊点卖玩具,已知小成所有玩具的进价均为2元/件,在销售过程中发现:每天玩具的销售量y(件)与销售单价x(元/件)的关系如图7所示,其中AB段为反比例函数图象的一部分,BC段为一次函数图象的一部分,设小成销售这种玩具的日利润为w元.
(1)根据图象,求出y与x之间的函数解析式;
(2)若小成某天将玩具的销售单价定为超过4元/件(x>4),且销售利润为54元,求该天玩具的销售单价.
图7
9.某食品加工厂以2万元引进一条新的生产加工线.已知加工这种食品的成本价为每袋20元,物价部门规定该食品的市场销售单价不得高于每袋35元.该食品的月销售量y(千袋)与销售单价x(元/袋)之间具有以下函数关系:
y=
(注:月获利=月销售收入-生产成本-投资成本)
(1)当销售单价定为25元/袋时,该食品加工厂的月销售量为多少千袋?
(2)求该食品加工厂的月获利M(千元)与销售单价x(元/袋)之间的函数解析式.
(3)判断当销售单价x(元/袋)的范围为30命题点6 反比例函数在物理学科中的应用
10.公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1200
N和0.5
m,则动力F(单位:N)关于动力臂l(单位:m)的函数解析式是
( )
A.F=
B.F=
C.F=
D.F=
11.在温度不变的条件下,通过一次又一次地对气缸顶部的活塞加压,测出每一次加压后气体对气缸壁产生的压强P(kPa)与气缸内气体的体积V(mL)的关系可以用如图26-2-8所示的反比例函数的图象进行表示,下列说法错误的是
( )
图26-2-8
A.气压P与体积V的函数解析式为P=,且k>0
B.当气压P=70时,体积V的取值范围为70C.当体积V变为原来的时,对应的气压P变为原来的
D.当60≤V≤100时,气压P随着体积V的增大而减小
12.如图,电源两端的电压U保持不变,电流强度I与总电阻R成反比例.在实验课上,通过不断调整滑动变阻器的电阻来改变灯泡的亮度.实验测得,当电路中的总电阻R为15
Ω时,通过的电流强度I为0.4
A.
(1)求电流强度I关于总电阻R的函数解析式,并说明比例系数的实际意义;
(2)如果灯泡的电阻为5
Ω,电路中电流控制在0.3
A到0.6
A之间(包含0.3
A和0.6
A),那么这个滑动变阻器的电阻应控制在什么范围?
(3)若电路中的总电阻扩大到原来的n倍,则所通过的电流将怎样变化?
13.如图,李老师设计了一个探究杠杆平衡条件的试验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.试验数据记录如下表:
x(cm)
10
15
20
25
30
y(g)
30
20
15
12
10
(1)猜测y与x之间的函数关系,并求出函数解析式;
(2)当砝码的质量为24
g时,活动托盘B与点O的距离是多少?
(3)将活动托盘B往左移动时,应往活动托盘B中添加还是减少砝码?
答案
1.A
2.解:(1)根据题意,得xy=18,即y=(0(2)由y=,且x,y都是正整数,可知x可取1,2,3,6,9,18,
但x≤8,x+2y≤18,所以符合条件的有x=3,y=6;x=6,y=3.
答:满足条件的围建方案有AD=6
m,CD=3
m和AD=3
m,CD=6
m.
3.解:(1)设y与x之间的函数解析式为y=.
∵点(24,50)在其图象上,∴k=24×50=1200,
∴y与x之间的函数解析式为y=(x>0).
(2)2台挖掘机每天能够开挖水渠30×2=60(米),即x=60,则y===20.
故该工程队需要用20天才能完成此项任务.
(3)1200÷10=120(米).
故该工程队每天至少要完成120米.
4.3800 .
5.解:(1)观察可知,售价x与日销量y的乘积为定值300,则y与x之间的关系为反比例函数.
设y与x之间的函数解析式为y=.
∵当x=10时,y=30,
∴k=300,∴y=.
把其余各组对应值代入上式,均成立,
故y与x之间的函数解析式为y=(x≥10).
(2)能达到200元.
理由:依题意,得(x-10)·=200,
解得x=30.
经检验,x=30是原方程的解,并且符合题意.
即当售价为30元/kg时,水果店销售该种水果的日利润为200元.
6.解:(1)∵该反比例函数t=的图象经过点A(35,1.2),∴1.2=,解得k=42,
∴t与v之间的函数解析式为t=.
把B(m,0.5)代入t=,
得0.5=,解得m=84.
(2)由题意,得≤60,解得t≥0.7.
答:汽车通过该路段至少需要0.7
h.
7.解:(1)根据表中的数据,可设平均速度v(千米/时)关于行驶时间t(时)的函数解析式为v=.
∵当v=75时,t=4,∴k=75×4=300,∴v=.
经检验,其他数据均满足该函数解析式.
∵汽车行驶速度不超过100千米/时,v≤100,∴t≥3.
故平均速度v(千米/时)关于行驶时间t(时)的函数解析式为v=(t≥3).
(2)不能.理由如下:
当t=2.5时,v==120>100,
∴汽车上午7:30从超越公司出发,不能在上午10:00之前到达新时代市场.
8.解:(1)当2≤x≤4时,设y=.
将A(2,40)代入,得k1=2×40=80,
∴当2≤x≤4时,y与x之间的函数解析式为y=.
当4将B(4,20),C(14,0)代入,得
解得
∴当4综上,y与x之间的函数解析式为y=
(2)由题意,得(x-2)(-2x+28)=54,
解得x1=5,x2=11,
∴该天玩具的销售单价为5元/件或11元/件.
9.解:(1)当x=25时,y==24,
所以当销售单价定为25元/袋时,该食品加工厂的月销售量为24千袋.
(2)当20当30故该食品加工厂的月获利M(千元)与销售单价x(元/袋)之间的函数解析式为
M=
(3)当300,故该食品加工厂盈利;当x=35时,M取得最大值,M最大=0.5×352-220=392.5,392.5千元=39.25万元.
答:当销售单价x(元/袋)的范围为3010.B 11.B
12.解:(1)根据电学知识得U=IR.当R=15,I=0.4时,U=6,所以电流强度I关于总电阻R的函数解析式为I=.
比例系数6的实际意义为电源两端的电压为6
V.
(2)由(1)得R=.
当I=0.3时,R=20;当I=0.6时,R=10,
因为灯泡的电阻为5
Ω,所以滑动变阻器的电阻应控制在5~15
Ω之间.
(3)总电阻扩大到原来的n倍,由I=知,电流缩小为原来的.
13.解:(1)由表格猜测y与x之间的函数关系为反比例函数关系.
设y=,把x=10,y=30代入求得k=300,
∴y=.
将其余各组对应值代入均成立,
∴y与x之间的函数解析式为y=(x>0).
(2)把y=24代入y=,得x=12.5,
∴当砝码的质量为24
g时,活动托盘B与点O的距离是12.5
cm.
(3)应添加砝码.
命题点
1 利用反比例函数解决实际问题中的几何问题
1.一张正方形的纸片,剪去两个一样的小矩形得到一个“E”字形图案,如图1所示,设小矩形的长和宽分别为x,y,剪去部分的面积为20,若2≤x≤10,则y关于x的函数图象是
( )
图1
图2
2.如图3,学校打算用材料围建一个面积为18
m2的矩形生物园用来饲养小兔,其中矩形ABCD的一边AB靠墙,墙长为8
m,设AD的长为y
m,CD的长为x
m.
(1)求y与x之间的函数解析式;
(2)若围成矩形生物园的三边材料总长不超过18
m,材料AD和CD的长都是整数米,求出满足条件的所有围建方案.
图3
命题点
2 利用反比例函数解决实际问题中的工程问题
3.在工程实施过程中,某工程队接受一项开挖水渠的工程,所需天数y(天)与每天完成的工程量x(米)的函数关系图象如图4所示,是双曲线的一部分.
(1)请根据题意,求y与x之间的函数解析式;
(2)若该工程队有2台挖掘机,每台挖掘机每天能够开挖水渠30米,则该工程队需要用多少天才能完成此项任务?
(3)如果为了防汛工作的紧急需要,必须在10天内完成任务,那么该工程队每天至少要完成多少米?
图4
命题点
3 利用反比例函数解决实际问题中的商品销售问题
4.李老师参加了某电脑公司推出的分期付款购买电脑活动(无利息),他购买的电脑价格为9800元,交了首付之后每月付款y元,x个月结清贷款,y与x满足如图5所示的函数关系,通过以上信息可知李老师的首付款为 元.?
图5
5.水果店在销售某种水果,该种水果的进价为10元/kg.根据以往的销售经验可知:日销量y(单位:kg)随售价x(单位:元/kg)的变化规律符合某种函数关系.
该水果店以往的销售记录如下表:(售价不低于进价)
售价x(单位:元/kg)
10
15
20
25
30
日销量y(单位:kg)
30
20
15
12
10
若y与x之间的函数关系是一次函数、二次函数、反比例函数中的某一种.
(1)判断y与x之间的函数关系,并写出其解析式;
(2)水果店销售该种水果的日利润能否达到200元?说明理由.
命题点
4 利用反比例函数解决实际问题中的行程问题
6.一辆汽车通过某段公路时,行驶时间t(h)与行驶速度v(km/h)满足反比例函数关系t=,其图象为一段曲线(如图6),端点为A(35,1.2),B(m,0.5).
(1)求k和m的值;
(2)若该路段限速60
km/h,则汽车通过该路段至少需要多少时间?
图6
7.超越公司将某品牌农副产品运往新时代市场进行销售,记汽车的行驶时间为t(时),平均速度为v(千米/时)(汽车行驶速度不超过100千米/时).根据经验,v,t的几组对应值如下表:
v(千米/时)
75
80
85
90
95
t(时)
4.00
3.75
3.53
3.33
3.16
(1)根据表中的数据,求出平均速度v(千米/时)关于行驶时间t(时)的函数解析式;
(2)汽车上午7:30从超越公司出发,能否在上午10:00之前到达新时代市场?说明理由.
命题点
5 反比例函数和一次函数在实际问题中的综合应用
8.[2019·成都金牛区月考]
小成利用暑期参加社会实践活动,在妈妈的帮助下,利用社区提供的免费摊点卖玩具,已知小成所有玩具的进价均为2元/件,在销售过程中发现:每天玩具的销售量y(件)与销售单价x(元/件)的关系如图7所示,其中AB段为反比例函数图象的一部分,BC段为一次函数图象的一部分,设小成销售这种玩具的日利润为w元.
(1)根据图象,求出y与x之间的函数解析式;
(2)若小成某天将玩具的销售单价定为超过4元/件(x>4),且销售利润为54元,求该天玩具的销售单价.
图7
9.某食品加工厂以2万元引进一条新的生产加工线.已知加工这种食品的成本价为每袋20元,物价部门规定该食品的市场销售单价不得高于每袋35元.该食品的月销售量y(千袋)与销售单价x(元/袋)之间具有以下函数关系:
y=
(注:月获利=月销售收入-生产成本-投资成本)
(1)当销售单价定为25元/袋时,该食品加工厂的月销售量为多少千袋?
(2)求该食品加工厂的月获利M(千元)与销售单价x(元/袋)之间的函数解析式.
(3)判断当销售单价x(元/袋)的范围为30
10.公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1200
N和0.5
m,则动力F(单位:N)关于动力臂l(单位:m)的函数解析式是
( )
A.F=
B.F=
C.F=
D.F=
11.在温度不变的条件下,通过一次又一次地对气缸顶部的活塞加压,测出每一次加压后气体对气缸壁产生的压强P(kPa)与气缸内气体的体积V(mL)的关系可以用如图26-2-8所示的反比例函数的图象进行表示,下列说法错误的是
( )
图26-2-8
A.气压P与体积V的函数解析式为P=,且k>0
B.当气压P=70时,体积V的取值范围为70
D.当60≤V≤100时,气压P随着体积V的增大而减小
12.如图,电源两端的电压U保持不变,电流强度I与总电阻R成反比例.在实验课上,通过不断调整滑动变阻器的电阻来改变灯泡的亮度.实验测得,当电路中的总电阻R为15
Ω时,通过的电流强度I为0.4
A.
(1)求电流强度I关于总电阻R的函数解析式,并说明比例系数的实际意义;
(2)如果灯泡的电阻为5
Ω,电路中电流控制在0.3
A到0.6
A之间(包含0.3
A和0.6
A),那么这个滑动变阻器的电阻应控制在什么范围?
(3)若电路中的总电阻扩大到原来的n倍,则所通过的电流将怎样变化?
13.如图,李老师设计了一个探究杠杆平衡条件的试验:在一个自制类似天平的仪器的左边固定托盘A中放置一个重物,在右边活动托盘B(可左右移动)中放置一定质量的砝码,使得仪器左右平衡.改变活动托盘B与点O的距离x(cm),观察活动托盘B中砝码的质量y(g)的变化情况.试验数据记录如下表:
x(cm)
10
15
20
25
30
y(g)
30
20
15
12
10
(1)猜测y与x之间的函数关系,并求出函数解析式;
(2)当砝码的质量为24
g时,活动托盘B与点O的距离是多少?
(3)将活动托盘B往左移动时,应往活动托盘B中添加还是减少砝码?
答案
1.A
2.解:(1)根据题意,得xy=18,即y=(0
但x≤8,x+2y≤18,所以符合条件的有x=3,y=6;x=6,y=3.
答:满足条件的围建方案有AD=6
m,CD=3
m和AD=3
m,CD=6
m.
3.解:(1)设y与x之间的函数解析式为y=.
∵点(24,50)在其图象上,∴k=24×50=1200,
∴y与x之间的函数解析式为y=(x>0).
(2)2台挖掘机每天能够开挖水渠30×2=60(米),即x=60,则y===20.
故该工程队需要用20天才能完成此项任务.
(3)1200÷10=120(米).
故该工程队每天至少要完成120米.
4.3800 .
5.解:(1)观察可知,售价x与日销量y的乘积为定值300,则y与x之间的关系为反比例函数.
设y与x之间的函数解析式为y=.
∵当x=10时,y=30,
∴k=300,∴y=.
把其余各组对应值代入上式,均成立,
故y与x之间的函数解析式为y=(x≥10).
(2)能达到200元.
理由:依题意,得(x-10)·=200,
解得x=30.
经检验,x=30是原方程的解,并且符合题意.
即当售价为30元/kg时,水果店销售该种水果的日利润为200元.
6.解:(1)∵该反比例函数t=的图象经过点A(35,1.2),∴1.2=,解得k=42,
∴t与v之间的函数解析式为t=.
把B(m,0.5)代入t=,
得0.5=,解得m=84.
(2)由题意,得≤60,解得t≥0.7.
答:汽车通过该路段至少需要0.7
h.
7.解:(1)根据表中的数据,可设平均速度v(千米/时)关于行驶时间t(时)的函数解析式为v=.
∵当v=75时,t=4,∴k=75×4=300,∴v=.
经检验,其他数据均满足该函数解析式.
∵汽车行驶速度不超过100千米/时,v≤100,∴t≥3.
故平均速度v(千米/时)关于行驶时间t(时)的函数解析式为v=(t≥3).
(2)不能.理由如下:
当t=2.5时,v==120>100,
∴汽车上午7:30从超越公司出发,不能在上午10:00之前到达新时代市场.
8.解:(1)当2≤x≤4时,设y=.
将A(2,40)代入,得k1=2×40=80,
∴当2≤x≤4时,y与x之间的函数解析式为y=.
当4
解得
∴当4
(2)由题意,得(x-2)(-2x+28)=54,
解得x1=5,x2=11,
∴该天玩具的销售单价为5元/件或11元/件.
9.解:(1)当x=25时,y==24,
所以当销售单价定为25元/袋时,该食品加工厂的月销售量为24千袋.
(2)当20
M=
(3)当30
答:当销售单价x(元/袋)的范围为30
12.解:(1)根据电学知识得U=IR.当R=15,I=0.4时,U=6,所以电流强度I关于总电阻R的函数解析式为I=.
比例系数6的实际意义为电源两端的电压为6
V.
(2)由(1)得R=.
当I=0.3时,R=20;当I=0.6时,R=10,
因为灯泡的电阻为5
Ω,所以滑动变阻器的电阻应控制在5~15
Ω之间.
(3)总电阻扩大到原来的n倍,由I=知,电流缩小为原来的.
13.解:(1)由表格猜测y与x之间的函数关系为反比例函数关系.
设y=,把x=10,y=30代入求得k=300,
∴y=.
将其余各组对应值代入均成立,
∴y与x之间的函数解析式为y=(x>0).
(2)把y=24代入y=,得x=12.5,
∴当砝码的质量为24
g时,活动托盘B与点O的距离是12.5
cm.
(3)应添加砝码.
