人教版七年级上册数学 1.5.1乘方 课件(17张ppt)
文档属性
| 名称 | 人教版七年级上册数学 1.5.1乘方 课件(17张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 269.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-21 16:54:24 | ||
图片预览




文档简介
(共17张PPT)
边长为3的正方形
的面积是______.
3×3可以记作___,
读作_________.
3
3
3×3
32
3的平方
9
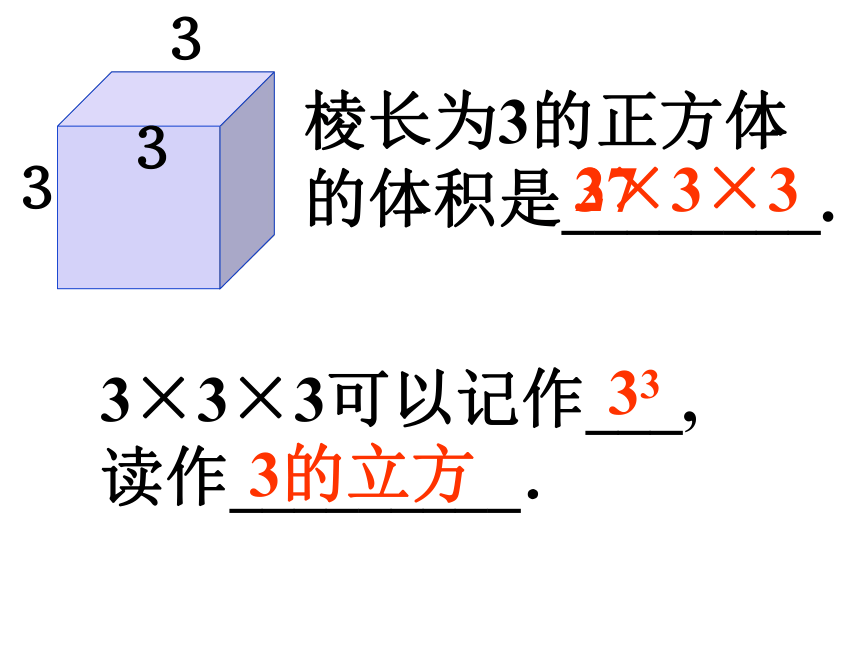
棱长为3的正方体
的体积是________.
3×3×3可以记作___,
读作_________.
3
3
3
3×3×3
33
3的立方
27
3
3
3
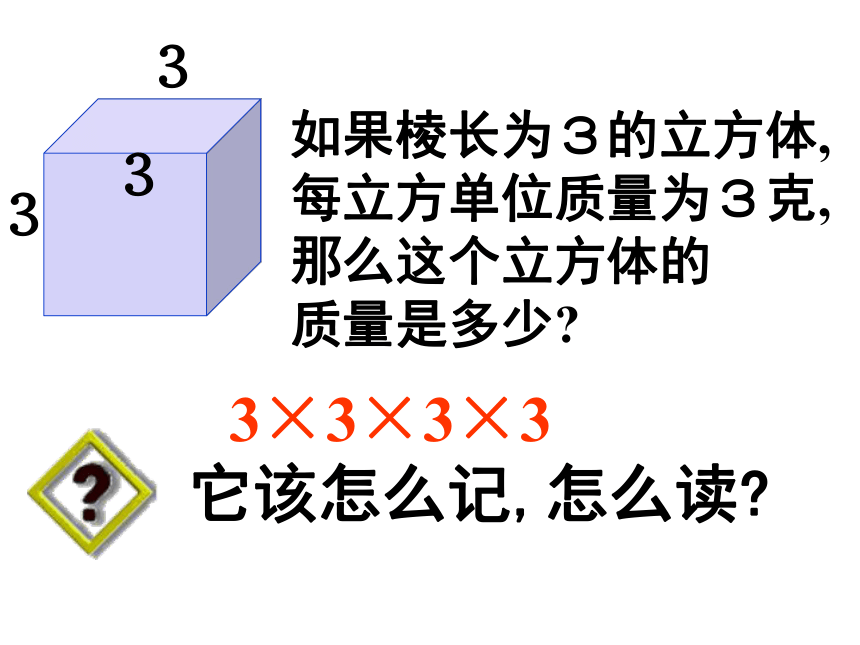
如果棱长为3的立方体,
每立方单位质量为3克,
那么这个立方体的
质量是多少?
它该怎么记,怎么读?
3×3×3×3
1.5.1
乘
方
一般地,n个相同的因数a相乘,即
求n个相同因数的积的运算叫做
乘方,乘方的结果叫幂.
,记作
,读作
a的n次方.
n个
a
·
a
·
…
·
a
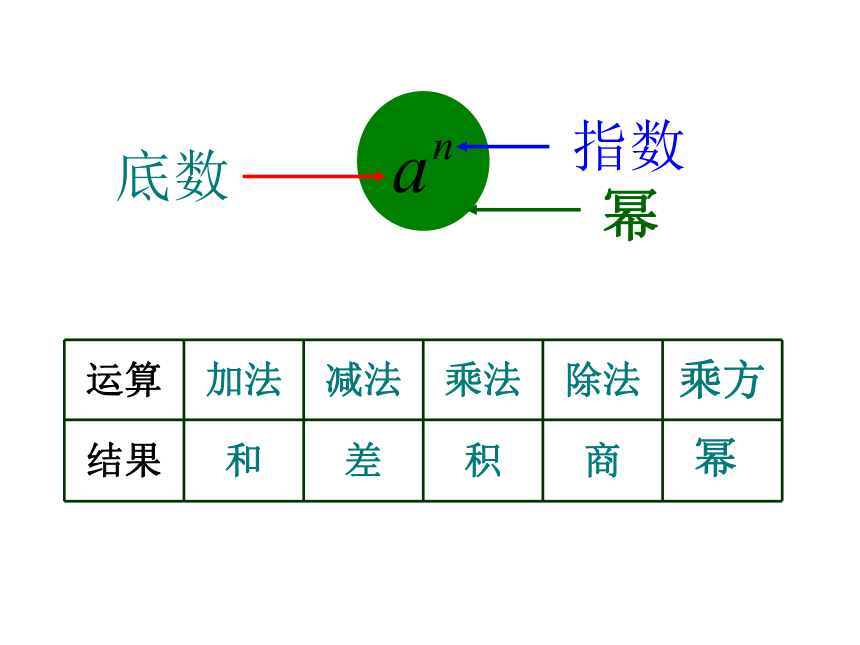
底数
指数
幂
运算
加法
减法
乘法
除法
乘方
结果
和
差
积
商
幂
(
1)23中底数是
,指数是
.
(2)在
中底数是
,指数是
.
(3)在8中底数是
,指数是
.
练一练
2
3
2
8
1
一个数可以看成这个数本身的一次幂,
指数1通常省略不写。
把下列各式写成乘方运算的形式,并指出底数,指数各是什么?
1.
5×5×5×5×5
2.(-1.3)×(-1.3)×(-1.3)×(-1.3)×(-1.3)
3.
4.
=55
=
(-1.3)
5
=
m
2a
1.
53;
2.
;
3.
;
4.
(-3)2
;
5.
-32;
6.
0100.
0的任何正整数次幂都是0
因为an就是n个a相乘,所以可以利用有理数的乘法运算进行有理数的乘方运算.
例1.计算
(1)
①41=
;
②23
=
;
③32
=
;
④14=
;
(2)
①(-4)1=
;
②(-2)5=
;
③(-3)3
=
;
④(-1)7=
;
(3)
①(-4)2
=
;
②(-2)6
=
;
③(-3)4
=
;
④(-1)8
=
;
4
9
8
1
-4
-27
-32
-1
16
81
64
1
观察此例题,你发现了什么规律?
一个正数的任何次幂都是___数;
正
一个负数的偶次幂是__数,奇次幂是__数.
正
负
判断下列各幂是正的还是负的
(1)
(-7)9
(2)
(-3)6
(3)
(-1)101
正
负
负
负
正
(5)
(-2)4
正
(4)
(6)
负
(7)
-(-2)4
负
(8)
-24
1、判断下列各题是否正确
①
23=2
×3
(
)
②
2+2+2=23
(
)
③
23=2×2
×2
(
)
×
√
×
火眼金睛
收获知多少?
1.求n个相同因数的积的运算叫______,积的结果叫做___,相同因数的个数叫做_____.
2.求乘方的方法是用_____运算.
.
3.乘方的运算法则是:
乘方
幂
指数
乘法
正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数;0的任何正整数次幂是0.
4.如果a、b互为相反数,那么
a2n=b2n,a2n+1+b2n+1=0
.
1次
2次
20次
把一张长方形的纸多次对折,所产生的纸的层数和对折的次数有关系吗?
对折
次数
1次
2次
3次
4次
5次
…
纸的
层数
…
层数可
表示为
…
2
4
8
16
32
2
2×2×2
2×2×2×2
2×2×2×2×2
2×2
如果对折n次,那么纸的层数是_____.
2n
有人说折30次纸的高度能超过珠穆朗玛峰的高度你信吗?
“乘方”精神:虽然是简简单单的重复,但结果却是惊人的.做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的.
作业布置:
(1)
102
(2)(-10)2
103
(-10)3
104
(-10)4
=100
=1000
=10000
=100
=-1000
=10000
想一想:观察结果,你能发现什么规律?
边长为3的正方形
的面积是______.
3×3可以记作___,
读作_________.
3
3
3×3
32
3的平方
9
棱长为3的正方体
的体积是________.
3×3×3可以记作___,
读作_________.
3
3
3
3×3×3
33
3的立方
27
3
3
3
如果棱长为3的立方体,
每立方单位质量为3克,
那么这个立方体的
质量是多少?
它该怎么记,怎么读?
3×3×3×3
1.5.1
乘
方
一般地,n个相同的因数a相乘,即
求n个相同因数的积的运算叫做
乘方,乘方的结果叫幂.
,记作
,读作
a的n次方.
n个
a
·
a
·
…
·
a
底数
指数
幂
运算
加法
减法
乘法
除法
乘方
结果
和
差
积
商
幂
(
1)23中底数是
,指数是
.
(2)在
中底数是
,指数是
.
(3)在8中底数是
,指数是
.
练一练
2
3
2
8
1
一个数可以看成这个数本身的一次幂,
指数1通常省略不写。
把下列各式写成乘方运算的形式,并指出底数,指数各是什么?
1.
5×5×5×5×5
2.(-1.3)×(-1.3)×(-1.3)×(-1.3)×(-1.3)
3.
4.
=55
=
(-1.3)
5
=
m
2a
1.
53;
2.
;
3.
;
4.
(-3)2
;
5.
-32;
6.
0100.
0的任何正整数次幂都是0
因为an就是n个a相乘,所以可以利用有理数的乘法运算进行有理数的乘方运算.
例1.计算
(1)
①41=
;
②23
=
;
③32
=
;
④14=
;
(2)
①(-4)1=
;
②(-2)5=
;
③(-3)3
=
;
④(-1)7=
;
(3)
①(-4)2
=
;
②(-2)6
=
;
③(-3)4
=
;
④(-1)8
=
;
4
9
8
1
-4
-27
-32
-1
16
81
64
1
观察此例题,你发现了什么规律?
一个正数的任何次幂都是___数;
正
一个负数的偶次幂是__数,奇次幂是__数.
正
负
判断下列各幂是正的还是负的
(1)
(-7)9
(2)
(-3)6
(3)
(-1)101
正
负
负
负
正
(5)
(-2)4
正
(4)
(6)
负
(7)
-(-2)4
负
(8)
-24
1、判断下列各题是否正确
①
23=2
×3
(
)
②
2+2+2=23
(
)
③
23=2×2
×2
(
)
×
√
×
火眼金睛
收获知多少?
1.求n个相同因数的积的运算叫______,积的结果叫做___,相同因数的个数叫做_____.
2.求乘方的方法是用_____运算.
.
3.乘方的运算法则是:
乘方
幂
指数
乘法
正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数;0的任何正整数次幂是0.
4.如果a、b互为相反数,那么
a2n=b2n,a2n+1+b2n+1=0
.
1次
2次
20次
把一张长方形的纸多次对折,所产生的纸的层数和对折的次数有关系吗?
对折
次数
1次
2次
3次
4次
5次
…
纸的
层数
…
层数可
表示为
…
2
4
8
16
32
2
2×2×2
2×2×2×2
2×2×2×2×2
2×2
如果对折n次,那么纸的层数是_____.
2n
有人说折30次纸的高度能超过珠穆朗玛峰的高度你信吗?
“乘方”精神:虽然是简简单单的重复,但结果却是惊人的.做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的.
作业布置:
(1)
102
(2)(-10)2
103
(-10)3
104
(-10)4
=100
=1000
=10000
=100
=-1000
=10000
想一想:观察结果,你能发现什么规律?
