高中物理必修二万有引力定律的应用课件25张PPT
文档属性
| 名称 | 高中物理必修二万有引力定律的应用课件25张PPT |

|
|
| 格式 | pptx | ||
| 文件大小 | 380.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-20 12:49:44 | ||
图片预览







文档简介
万有引力定律的应用
3.3
一、万有引力定律应用的两条基本思路
二、应用题型举例
1.中心体质量的计算
2.中心体密度的计算
3.卫星各运动学量的比较
4.发现未知天体
5.双星问题
海王星是亚当斯和勒维耶同时预言的,伽勒耶证实。冥王星是汤姆博夫发现的。
1.哪位物理学家根据万有引力定理预言哈雷彗星1758年回归,是谁修正了他的预言并得到了证实?
3.课本上计算地球质量的原理是什么?计算太阳质量的原理又是什么?
2.海王星是怎样发现的?冥王星是谁发现的?
地球质量是利用重力等于万有引力求得的,太阳质量是利用地球绕太阳做匀速圆周运动求得的。
阅读教材P49-50页,回答以下问题:
哈雷 ;克雷洛
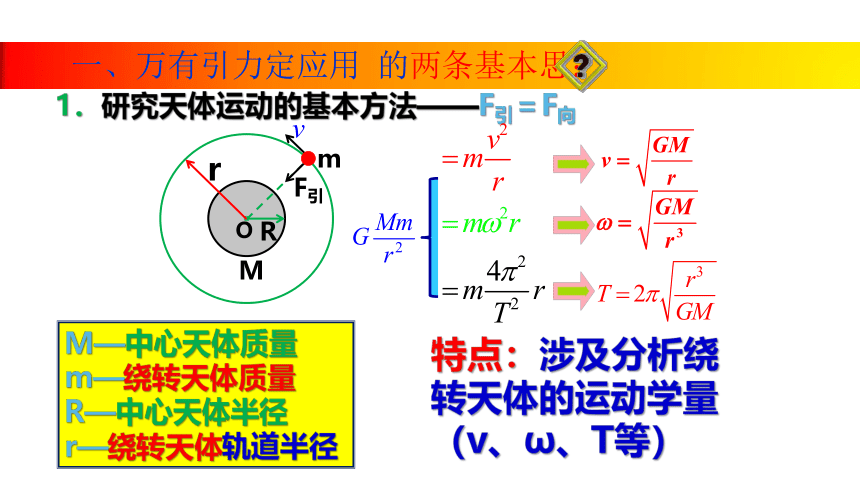
F引
r
M
R
O
m
1.研究天体运动的基本方法——F引=F向
M—中心天体质量
m—绕转天体质量
R—中心天体半径
r—绕转天体轨道半径
特点:涉及分析绕转天体的运动学量(v、ω、T等)
一、万有引力定应用 的两条基本思:
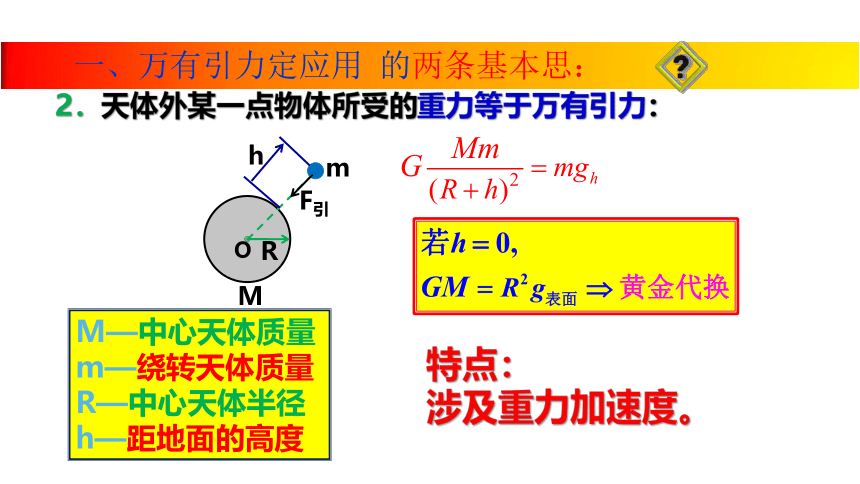
2.天体外某一点物体所受的重力等于万有引力:
M—中心天体质量
m—绕转天体质量
R—中心天体半径
h—距地面的高度
特点:
涉及重力加速度。
F引
M
R
O
m
h
一、万有引力定应用 的两条基本思:
方法一:
已知天体的球体半径R和球体表面重力加速度g.求天体的质量M
基本思路:
二、应用 一天体质量的计算:
【例1 】 :设地球表面重力加速度为g0,物体在距离地心4R(R是地球的半径)处,由于地球的作用而产生的加速度为g,则g/g0为多少?
解析:
由题设条件知:地球对物体的引力应等于物体的重力,即:
【例2】:某个行星质量是地球质量的一半,半径也是地球的一半,那么一个物体在此行星上的重力加速度是地球上的重力加速度的多少倍?
解析:
由题设条件知:星球对物体的引力应等于物体的重力,即:
【例3】、某个行星的质量是地球质量的一半,半径也是地球的一半,某人在地球上能举起100kg的重物,若在该行星上最多能举起质量为多少千克的物体?(地球表面的重力加速度g取9.8m/s2)
解析:
方法二:
已知行星(或卫星)的公转周期T、轨道半径r,可求出中心天体的质量M(但不能求出行星或卫星的质量m)
二、应用 一—天体质量的计算:
基本思路:
二、应用 一—天体质量的计算:
【例4】:把地球绕太阳公转看做是匀速圆周运动,轨道平均半径约为1.5×108km,已知引力常量G=6.67×10-11N· m2/kg2,则可估算出太阳的质量大约是多少kg?(结果取一位有效数字)
=
基本思路:
根据上面两种方式算出中心天体的质量M,结合球体体积计算公式:
物体的密度计算公式求出中心天体的密度:
二、应用 二—天体密度的计算:
二、应用 二—天体密度的计算:
当r≈R时
二、应用 二—天体密度的计算:
【例5】 、一艘宇宙飞船飞近某一个不知名的行星,并进入靠近该行星表面的圆形轨道,宇航员进行预定的考察工作,宇航员能不能仅用一只表通过测定时间来测定该行星的密度?说明理由及推导过程。
分析:使宇宙飞船靠近行星表面做匀速圆周运动(r=R),用表测出飞船飞行一圈的时间T即可:
=
r=R
二、应用 三—比较卫星的运动学量:
【例6】 :如图所示,a、b、c是地球的大气层外圆形轨道上运行的三颗卫星,a和b质量相等且小于c的质量,则( )
A.b所需向心力最小
B.b、c的周期相同且大于a的周期
C.b、c的向心加速度大小相等,且大于a的向心加速度
D.b、c的线速度大小相等,且小于a的线速度
ABD
地球
a
b
c
基本方法:
⑴双星做圆周运动的向心力均为相同的引力:
⑵双星运动周期T相等。
⑶轨道半径之和恒定:
r1+r2=L
二、应用 四—双星问题:
m1
m2
O
L
r1
r2
ω
ω
【例7】 :经过天文望远镜长期观察,人们在宇宙中已经发现了许多双星系统。
双星系统由两个星体构成,其中每个星体的线度都远小于它们之间的距离,一般双星系统距离其他星体很远,可以当作孤立系统处理。
现观察到一对双星A、B绕它们连线上的一点做匀速圆周运动,其周期为T,A、B之间的距离为L,它们的线速度之比v1/v2=2,试求这两颗星体的质量。
解:
m1
m2
O
L
r1
r2
ω
ω
由题设条件,设运动草图如下,则:
对于m1:
…①
对于m2:
…②
…③
…④
由③④式,解得:r1=2L/3,r2=L/3 …⑤
由①②⑤式,解得:
二、应用五—发现未知天体:
基本思路:
当一个已知行星的实际轨道和理论计算的轨道之间有较大的误差时,说明还有未知的天体给这个行星施加引力.
理论指导实践
预测未知天体——海王星、冥王星的发现
万有引力对研究天体运动有着重要的意义。海王星、冥王星就是根据万有引力定律发现的。在18世纪发现的第七个行星——天王星的运动轨道,总是同根据万有引力定律计算出来的有一定偏离。当时有人预测,肯定在其轨道外还有一颗未发现的新星。后来,亚当斯和勒维耶在预言位置的附近找到了这颗新星(海王星)。后来,科学家利用这一原理还发现了太阳系的第9颗行星——冥王星,由此可见,万有引力定律在天文学上的应用,有极为重要的意义。
1、行星的发现
开普勒时代 :5大行星
18世纪 : 7大行星根据轨道的偏离计算出第8大行星——海王星。
2、一次失败的理论计算,后来发现了第九大行星——冥王星
二、应用五—发现未知天体:
背景:
1781年由英国物理学家威廉.赫歇尔发现了天王星,但人们观测到的天王星的运行轨迹与万有引力定律推测的结果有一些误差……
1.1845年英国人亚当斯和法国天文学家勒维耶各自独立用万有引力定律计算发现了“海王星”(第8个行星)。
2.1930年3月14日人们发现了从被称为太阳系第9个行星— 冥王星
3.1978年人们又发现了冥王星的卫星——卡戎
再见
3.3
一、万有引力定律应用的两条基本思路
二、应用题型举例
1.中心体质量的计算
2.中心体密度的计算
3.卫星各运动学量的比较
4.发现未知天体
5.双星问题
海王星是亚当斯和勒维耶同时预言的,伽勒耶证实。冥王星是汤姆博夫发现的。
1.哪位物理学家根据万有引力定理预言哈雷彗星1758年回归,是谁修正了他的预言并得到了证实?
3.课本上计算地球质量的原理是什么?计算太阳质量的原理又是什么?
2.海王星是怎样发现的?冥王星是谁发现的?
地球质量是利用重力等于万有引力求得的,太阳质量是利用地球绕太阳做匀速圆周运动求得的。
阅读教材P49-50页,回答以下问题:
哈雷 ;克雷洛
F引
r
M
R
O
m
1.研究天体运动的基本方法——F引=F向
M—中心天体质量
m—绕转天体质量
R—中心天体半径
r—绕转天体轨道半径
特点:涉及分析绕转天体的运动学量(v、ω、T等)
一、万有引力定应用 的两条基本思:
2.天体外某一点物体所受的重力等于万有引力:
M—中心天体质量
m—绕转天体质量
R—中心天体半径
h—距地面的高度
特点:
涉及重力加速度。
F引
M
R
O
m
h
一、万有引力定应用 的两条基本思:
方法一:
已知天体的球体半径R和球体表面重力加速度g.求天体的质量M
基本思路:
二、应用 一天体质量的计算:
【例1 】 :设地球表面重力加速度为g0,物体在距离地心4R(R是地球的半径)处,由于地球的作用而产生的加速度为g,则g/g0为多少?
解析:
由题设条件知:地球对物体的引力应等于物体的重力,即:
【例2】:某个行星质量是地球质量的一半,半径也是地球的一半,那么一个物体在此行星上的重力加速度是地球上的重力加速度的多少倍?
解析:
由题设条件知:星球对物体的引力应等于物体的重力,即:
【例3】、某个行星的质量是地球质量的一半,半径也是地球的一半,某人在地球上能举起100kg的重物,若在该行星上最多能举起质量为多少千克的物体?(地球表面的重力加速度g取9.8m/s2)
解析:
方法二:
已知行星(或卫星)的公转周期T、轨道半径r,可求出中心天体的质量M(但不能求出行星或卫星的质量m)
二、应用 一—天体质量的计算:
基本思路:
二、应用 一—天体质量的计算:
【例4】:把地球绕太阳公转看做是匀速圆周运动,轨道平均半径约为1.5×108km,已知引力常量G=6.67×10-11N· m2/kg2,则可估算出太阳的质量大约是多少kg?(结果取一位有效数字)
=
基本思路:
根据上面两种方式算出中心天体的质量M,结合球体体积计算公式:
物体的密度计算公式求出中心天体的密度:
二、应用 二—天体密度的计算:
二、应用 二—天体密度的计算:
当r≈R时
二、应用 二—天体密度的计算:
【例5】 、一艘宇宙飞船飞近某一个不知名的行星,并进入靠近该行星表面的圆形轨道,宇航员进行预定的考察工作,宇航员能不能仅用一只表通过测定时间来测定该行星的密度?说明理由及推导过程。
分析:使宇宙飞船靠近行星表面做匀速圆周运动(r=R),用表测出飞船飞行一圈的时间T即可:
=
r=R
二、应用 三—比较卫星的运动学量:
【例6】 :如图所示,a、b、c是地球的大气层外圆形轨道上运行的三颗卫星,a和b质量相等且小于c的质量,则( )
A.b所需向心力最小
B.b、c的周期相同且大于a的周期
C.b、c的向心加速度大小相等,且大于a的向心加速度
D.b、c的线速度大小相等,且小于a的线速度
ABD
地球
a
b
c
基本方法:
⑴双星做圆周运动的向心力均为相同的引力:
⑵双星运动周期T相等。
⑶轨道半径之和恒定:
r1+r2=L
二、应用 四—双星问题:
m1
m2
O
L
r1
r2
ω
ω
【例7】 :经过天文望远镜长期观察,人们在宇宙中已经发现了许多双星系统。
双星系统由两个星体构成,其中每个星体的线度都远小于它们之间的距离,一般双星系统距离其他星体很远,可以当作孤立系统处理。
现观察到一对双星A、B绕它们连线上的一点做匀速圆周运动,其周期为T,A、B之间的距离为L,它们的线速度之比v1/v2=2,试求这两颗星体的质量。
解:
m1
m2
O
L
r1
r2
ω
ω
由题设条件,设运动草图如下,则:
对于m1:
…①
对于m2:
…②
…③
…④
由③④式,解得:r1=2L/3,r2=L/3 …⑤
由①②⑤式,解得:
二、应用五—发现未知天体:
基本思路:
当一个已知行星的实际轨道和理论计算的轨道之间有较大的误差时,说明还有未知的天体给这个行星施加引力.
理论指导实践
预测未知天体——海王星、冥王星的发现
万有引力对研究天体运动有着重要的意义。海王星、冥王星就是根据万有引力定律发现的。在18世纪发现的第七个行星——天王星的运动轨道,总是同根据万有引力定律计算出来的有一定偏离。当时有人预测,肯定在其轨道外还有一颗未发现的新星。后来,亚当斯和勒维耶在预言位置的附近找到了这颗新星(海王星)。后来,科学家利用这一原理还发现了太阳系的第9颗行星——冥王星,由此可见,万有引力定律在天文学上的应用,有极为重要的意义。
1、行星的发现
开普勒时代 :5大行星
18世纪 : 7大行星根据轨道的偏离计算出第8大行星——海王星。
2、一次失败的理论计算,后来发现了第九大行星——冥王星
二、应用五—发现未知天体:
背景:
1781年由英国物理学家威廉.赫歇尔发现了天王星,但人们观测到的天王星的运行轨迹与万有引力定律推测的结果有一些误差……
1.1845年英国人亚当斯和法国天文学家勒维耶各自独立用万有引力定律计算发现了“海王星”(第8个行星)。
2.1930年3月14日人们发现了从被称为太阳系第9个行星— 冥王星
3.1978年人们又发现了冥王星的卫星——卡戎
再见
