高中物理必修二万有引力定律 _ 本章小结课件41张PPT
文档属性
| 名称 | 高中物理必修二万有引力定律 _ 本章小结课件41张PPT |  | |
| 格式 | ppt | ||
| 文件大小 | 8.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-20 12:55:53 | ||
图片预览











文档简介
第三章
万有引力定律
微专题:地球同步卫星、卫星变轨和双星问题
[学习目标]
1.掌握运用万有引力定律和圆周运动知识分析天体运动问题的基本思路.
2.理解赤道物体、同步卫星和近地卫星的区别.
3.会分析卫星的变轨问题,知道卫星变轨的原因和变轨前后卫星速度的变化.
4.掌握双星运动的特点,会分析求解双星问题.
要点知识回顾
Ⅰ
分析处理天体运动问题,要抓住
天体(卫星)运动问题的处理思路
“两个思路”
“三个不同”
“一个模型”
无论是自然天体(如行星等),还是人造天体(如人造卫星、空间站等),只要天体的运动轨迹为圆形,就可将其简化为质点的匀速圆周运动。
“一个模型”
“两个思路”
“三个不同”
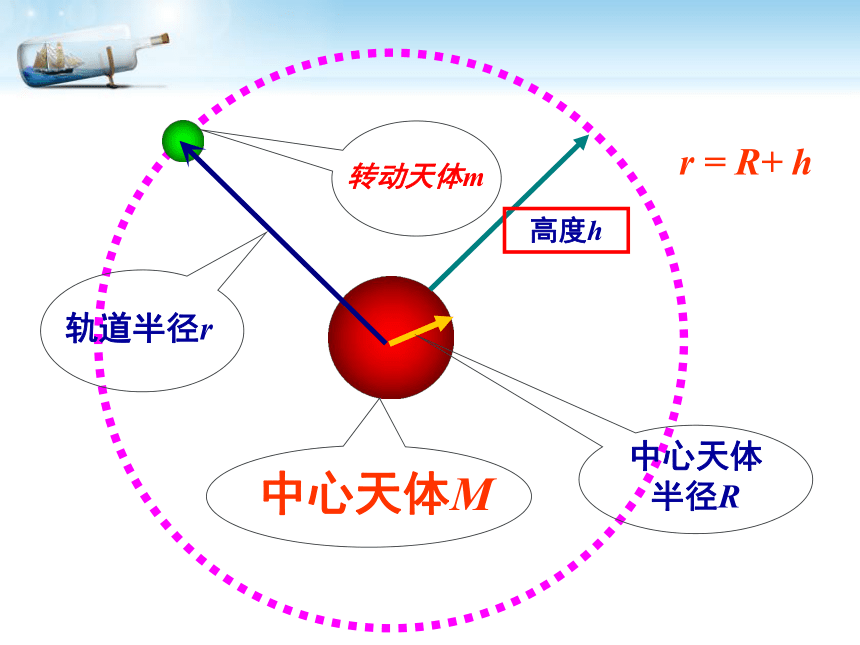
中心天体M
转动天体m
轨道半径r
中心天体
半径R
高度h
r = R+ h
③地球表面的物体随地球自转做匀速圆周运动的向心加速度a′=ω2Rcos θ,其中ω、R分别是地球的自转角速度和半径,θ是物体所在位置的纬度值.
1
知识点一
地球同步卫星
定义:
相对于地面静止且与地球自转具有相同周期(角速度)的卫星叫地球同步卫星.
地球同步卫星的实际轨道
地球同步卫星的实际轨道为赤道平面上离地面高度一定的圆轨道
地轴
地心o
F
(1)轨道平面一定:轨道平面与赤道平面共面.
(2)周期一定:与地球自转周期相同,即T=24 h.
(3)角速度一定:与地球自转的角速度相同.
(4)高度一定:由G =m (R+h)得地球同步卫星离地面的高度h=3.6×107 m.
(5)速率一定:v= =3.1×103 m/s.
(6)向心加速度一定:由G =ma得a= =gh,
即:同步卫星的向心加速度等于轨道处的重力加速度.
(7)绕行方向一定:运行方向与地球自转方向相同.
解决同步卫星问题的“四点”注意
2.重要手段:构建物理模型,绘制草图辅助分析.
3.物理规律:
(1)不快不慢:具有特定的运行线速度、角速度和周期.
(2)不高不低:具有特定的位置高度和轨道半径.
(3)不偏不倚:同步卫星的运行轨道平面必须处于地球赤道平面上,只能静止在赤道上方的特定的点上.
方法感悟
4.重要条件:
(1)地球的公转周期为1年,其自转周期为1天(24小时),地球的表面半径约为6.4×103 km,表面重力加速度g约为9.8 m/s2.
(2)月球的公转周期约27.3天,在一般估算中常取27天.
(3)人造地球卫星的运行半径最小为r=6.4×103 km,运行周期最小为T=84.8 min,运行速度最大为v=7.9 km/s.
1.为了同步卫星之间不互相干扰,大约3°左右才能放置1颗,这样地球的同步卫星只能有120颗。可见,空间位置也是一种资源。
2.同步卫星主要用于通讯。要实现全球通讯,只需三颗同步卫星即可。
例 如图所示,A为地面上的待发射卫星,B为近地圆轨道卫星,C为地球同步卫星.三颗卫星质量相同,三颗卫星的线速度大小分别为vA、vB、vC,角速度大小分别为ωA、ωB、ωC,周期分别为TA、TB、TC,向心加速度分别为aA、aB、aC,则
A.ωA=ωC<ωB
B.TA=TCC.vA=vCD.aA=aC>aB
√
近地卫星
近地卫星、赤道上物体及同步卫星的运行问题
三类卫星匀速圆周运动的比较
(1)轨道半径:r同>r近=r物.
(2)运行周期:T近(3)向心加速度:a近>a同>a物.
(4)动力学规律:
a.近地卫星和同步卫星都只由万有引力充当向心力.
b.赤道上的物体由万有引力和地面支持力的合力充当向心力,它的运动规律不同于卫星的运动规律.
赤道上的物体
同步卫星
易混辨析
比较a1和a2
同步卫星与赤道上物体的角速度相同
据a=ω2r分析
比较v1和v2
同步卫星与贴近地面的卫星皆由万有引力提供向心力
√
2
知识点二
卫星变轨问题
v
F引
F引=0
F引<F向
F引>F向
卫星变轨问题
M
m
速度—内小外大(看轨迹)
万有引力相同
卫星变轨问题
v
F引
1
2
R
卫星在圆轨道运行速度v1
v2
θ>900
减小
v3
F引
L
使卫星进入更高轨道做圆周运动
v3
v4
卫星的回收
例 如图所示为卫星发射过程的示意图,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再一次点火,将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,则当卫星分别在1、2、3轨道上正常运行时,以下说法中正确的是
A.卫星在轨道3上的速率大于在轨道1上的速率
B.卫星在轨道3上的周期大于在轨道2上的周期
C.卫星在轨道1上经过Q点时的速率大于它在轨道2上经过Q点时的速率
D.卫星在轨道2上经过P点时的加速度小于它在轨道3上经过P点时的加速度
√
飞船对接问题
(1)低轨道飞船与高轨道空间站对接如图甲所示,低轨道飞船通过合理地加速,沿椭圆轨道运动追上高轨道空间站与其完成对接.
(2)同一轨道飞船与空间站对接
如图乙所示,后面的飞船先减速降低高度,再加速提升高度,通过适当控制,使飞船追上空间站时恰好具有相同的速度.
√
3
知识点三
双星问题
两个靠得很近的天体,离其他天体非常遥远,它们以其连线上某一点O为圆心各自做匀速圆周运动,两者的距离保持不变,科学家把这样的两个天体称为“双星”
1.两颗恒星均围绕共同的旋转中心做匀速圆周运动。
2.两恒星之间万有引力分别提供了两恒星的向心力,即两颗恒星受到的向心力大小相等。
3.两颗恒星与旋转中心时刻三点共线,即两颗恒星角速度相同,周期相同。
双星运动的特点:
确定双星的旋转中心:
质量 m 越大,旋转半径越小,离旋转中心越近。
m1
m2
r1
r2
o
两个质量不同的天体构成双星系统,它们以二者连线上的某一点为圆心做匀速圆周运动,下列说法正确的是( )
A.质量大的天体线速度较大
B.质量小的天体角速度较大
C.两个天体的向心力大小一定相等
D.两个天体的向心加速度大小一定相等
√
(双星问题)如图所示,两颗星球组成的双星,在相互之间的万有引力作用下,绕连线上的O点做周期相同的匀速圆周运动.现测得两颗星之间的距离为L,质量之比为m1∶m2=3∶2,下列说法中正确的是
A.m1、m2做圆周运动的线速度之比为3∶2
B.m1、m2做圆周运动的角速度之比为3∶2
C.m1做圆周运动的半径为
D.m2做圆周运动的半径为L
√
挑战突破
(2013·山东理综·20)双星系统由两颗恒星组成,两恒星在相互引力的作用下,分别围绕其连线上的某一点做周期相同的匀速圆周运动.研究发现,双星系统演化过程中,两星的总质量、距离和周期均可能发生变化.若某双星系统中两星做圆周运动的周期为T,经过一段时间演化后,两星总质量变为原来的k倍,两星之间的距离变为原来的n倍,则此时圆周运动的周期为
√
设两恒星的质量分别为m1、m2,距离为L,
双星靠彼此的引力提供向心力,则有
并且r1+r2=L
当两星总质量变为原来的k倍,两星之间距离变为原来的n倍时
故选项B正确.
( )
1.地球同步卫星
2.卫星变轨问题
3.双星问题
“七个一定”
向心力大小相等、角速度相同、周期相同
线速度v发生变化导致需要的向心力发生变化,进而使轨道半径r发生变化
万有引力定律
微专题:地球同步卫星、卫星变轨和双星问题
[学习目标]
1.掌握运用万有引力定律和圆周运动知识分析天体运动问题的基本思路.
2.理解赤道物体、同步卫星和近地卫星的区别.
3.会分析卫星的变轨问题,知道卫星变轨的原因和变轨前后卫星速度的变化.
4.掌握双星运动的特点,会分析求解双星问题.
要点知识回顾
Ⅰ
分析处理天体运动问题,要抓住
天体(卫星)运动问题的处理思路
“两个思路”
“三个不同”
“一个模型”
无论是自然天体(如行星等),还是人造天体(如人造卫星、空间站等),只要天体的运动轨迹为圆形,就可将其简化为质点的匀速圆周运动。
“一个模型”
“两个思路”
“三个不同”
中心天体M
转动天体m
轨道半径r
中心天体
半径R
高度h
r = R+ h
③地球表面的物体随地球自转做匀速圆周运动的向心加速度a′=ω2Rcos θ,其中ω、R分别是地球的自转角速度和半径,θ是物体所在位置的纬度值.
1
知识点一
地球同步卫星
定义:
相对于地面静止且与地球自转具有相同周期(角速度)的卫星叫地球同步卫星.
地球同步卫星的实际轨道
地球同步卫星的实际轨道为赤道平面上离地面高度一定的圆轨道
地轴
地心o
F
(1)轨道平面一定:轨道平面与赤道平面共面.
(2)周期一定:与地球自转周期相同,即T=24 h.
(3)角速度一定:与地球自转的角速度相同.
(4)高度一定:由G =m (R+h)得地球同步卫星离地面的高度h=3.6×107 m.
(5)速率一定:v= =3.1×103 m/s.
(6)向心加速度一定:由G =ma得a= =gh,
即:同步卫星的向心加速度等于轨道处的重力加速度.
(7)绕行方向一定:运行方向与地球自转方向相同.
解决同步卫星问题的“四点”注意
2.重要手段:构建物理模型,绘制草图辅助分析.
3.物理规律:
(1)不快不慢:具有特定的运行线速度、角速度和周期.
(2)不高不低:具有特定的位置高度和轨道半径.
(3)不偏不倚:同步卫星的运行轨道平面必须处于地球赤道平面上,只能静止在赤道上方的特定的点上.
方法感悟
4.重要条件:
(1)地球的公转周期为1年,其自转周期为1天(24小时),地球的表面半径约为6.4×103 km,表面重力加速度g约为9.8 m/s2.
(2)月球的公转周期约27.3天,在一般估算中常取27天.
(3)人造地球卫星的运行半径最小为r=6.4×103 km,运行周期最小为T=84.8 min,运行速度最大为v=7.9 km/s.
1.为了同步卫星之间不互相干扰,大约3°左右才能放置1颗,这样地球的同步卫星只能有120颗。可见,空间位置也是一种资源。
2.同步卫星主要用于通讯。要实现全球通讯,只需三颗同步卫星即可。
例 如图所示,A为地面上的待发射卫星,B为近地圆轨道卫星,C为地球同步卫星.三颗卫星质量相同,三颗卫星的线速度大小分别为vA、vB、vC,角速度大小分别为ωA、ωB、ωC,周期分别为TA、TB、TC,向心加速度分别为aA、aB、aC,则
A.ωA=ωC<ωB
B.TA=TC
√
近地卫星
近地卫星、赤道上物体及同步卫星的运行问题
三类卫星匀速圆周运动的比较
(1)轨道半径:r同>r近=r物.
(2)运行周期:T近
(4)动力学规律:
a.近地卫星和同步卫星都只由万有引力充当向心力.
b.赤道上的物体由万有引力和地面支持力的合力充当向心力,它的运动规律不同于卫星的运动规律.
赤道上的物体
同步卫星
易混辨析
比较a1和a2
同步卫星与赤道上物体的角速度相同
据a=ω2r分析
比较v1和v2
同步卫星与贴近地面的卫星皆由万有引力提供向心力
√
2
知识点二
卫星变轨问题
v
F引
F引=0
F引<F向
F引>F向
卫星变轨问题
M
m
速度—内小外大(看轨迹)
万有引力相同
卫星变轨问题
v
F引
1
2
R
卫星在圆轨道运行速度v1
v2
θ>900
减小
v3
F引
L
使卫星进入更高轨道做圆周运动
v3
v4
卫星的回收
例 如图所示为卫星发射过程的示意图,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再一次点火,将卫星送入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P点,则当卫星分别在1、2、3轨道上正常运行时,以下说法中正确的是
A.卫星在轨道3上的速率大于在轨道1上的速率
B.卫星在轨道3上的周期大于在轨道2上的周期
C.卫星在轨道1上经过Q点时的速率大于它在轨道2上经过Q点时的速率
D.卫星在轨道2上经过P点时的加速度小于它在轨道3上经过P点时的加速度
√
飞船对接问题
(1)低轨道飞船与高轨道空间站对接如图甲所示,低轨道飞船通过合理地加速,沿椭圆轨道运动追上高轨道空间站与其完成对接.
(2)同一轨道飞船与空间站对接
如图乙所示,后面的飞船先减速降低高度,再加速提升高度,通过适当控制,使飞船追上空间站时恰好具有相同的速度.
√
3
知识点三
双星问题
两个靠得很近的天体,离其他天体非常遥远,它们以其连线上某一点O为圆心各自做匀速圆周运动,两者的距离保持不变,科学家把这样的两个天体称为“双星”
1.两颗恒星均围绕共同的旋转中心做匀速圆周运动。
2.两恒星之间万有引力分别提供了两恒星的向心力,即两颗恒星受到的向心力大小相等。
3.两颗恒星与旋转中心时刻三点共线,即两颗恒星角速度相同,周期相同。
双星运动的特点:
确定双星的旋转中心:
质量 m 越大,旋转半径越小,离旋转中心越近。
m1
m2
r1
r2
o
两个质量不同的天体构成双星系统,它们以二者连线上的某一点为圆心做匀速圆周运动,下列说法正确的是( )
A.质量大的天体线速度较大
B.质量小的天体角速度较大
C.两个天体的向心力大小一定相等
D.两个天体的向心加速度大小一定相等
√
(双星问题)如图所示,两颗星球组成的双星,在相互之间的万有引力作用下,绕连线上的O点做周期相同的匀速圆周运动.现测得两颗星之间的距离为L,质量之比为m1∶m2=3∶2,下列说法中正确的是
A.m1、m2做圆周运动的线速度之比为3∶2
B.m1、m2做圆周运动的角速度之比为3∶2
C.m1做圆周运动的半径为
D.m2做圆周运动的半径为L
√
挑战突破
(2013·山东理综·20)双星系统由两颗恒星组成,两恒星在相互引力的作用下,分别围绕其连线上的某一点做周期相同的匀速圆周运动.研究发现,双星系统演化过程中,两星的总质量、距离和周期均可能发生变化.若某双星系统中两星做圆周运动的周期为T,经过一段时间演化后,两星总质量变为原来的k倍,两星之间的距离变为原来的n倍,则此时圆周运动的周期为
√
设两恒星的质量分别为m1、m2,距离为L,
双星靠彼此的引力提供向心力,则有
并且r1+r2=L
当两星总质量变为原来的k倍,两星之间距离变为原来的n倍时
故选项B正确.
( )
1.地球同步卫星
2.卫星变轨问题
3.双星问题
“七个一定”
向心力大小相等、角速度相同、周期相同
线速度v发生变化导致需要的向心力发生变化,进而使轨道半径r发生变化
同课章节目录
- 第一章 抛体运动
- 1 认识曲线运动
- 2 运动的合成与分解
- 3 探究平抛运动的特点
- 4 研究平抛运动的规律
- 5 斜抛运动(选学)
- 第二章 匀速圆周运动
- 1 圆周运动
- 2 匀速圆周运动的向心力和向心加速度
- 3 圆周运动的实例分析
- 4 圆周运动与人类文明(选学)
- 第三章 万有引力定律
- 1 天体运动
- 2 万有引力定律
- 3 预言未知星体 计算天体质量
- 4 人造卫星宇宙
- 5 太空探索(选学)
- 第四章 机械能及其守恒定律
- 1 功
- 2 功率
- 3 动能 动能定理
- 4 势能
- 5 机械能守恒定律
- 6 实验:验证机械能守恒定律
- 第五章 经典力学的局限性与相对论初步
- 1 经典力学的成就与局限性
- 2 相对论时空观简介
- 3 宇宙的起源和演化
