北师大版 数学八年级上册第四章一次函数4.3一次函数的图象 同步练习 (word含答案)
文档属性
| 名称 | 北师大版 数学八年级上册第四章一次函数4.3一次函数的图象 同步练习 (word含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 323.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-20 00:00:00 | ||
图片预览

文档简介
4.3
一次函数的图象同步练习
选择题
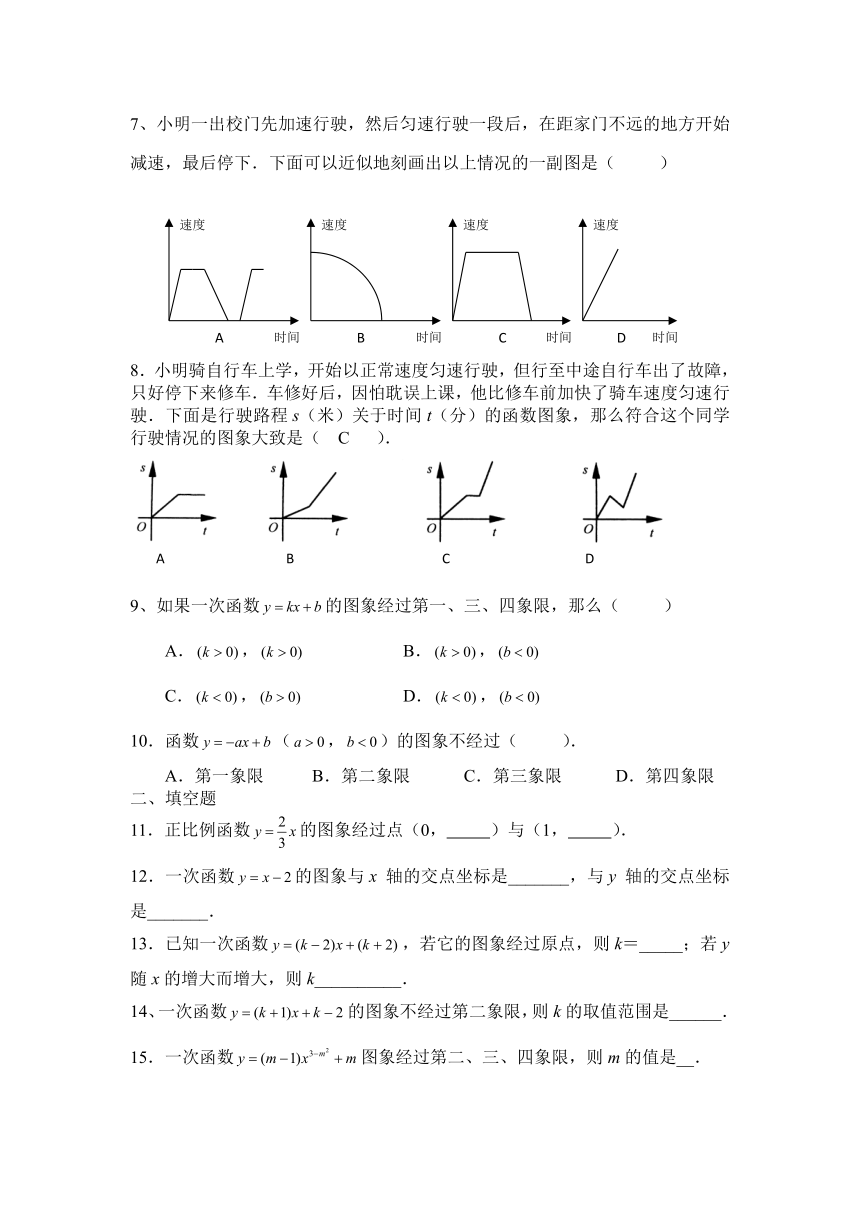
1、为了节能减排,鼓励居民节约用电,某市出台了新的居民用电收费标准:(1)若每户居民每月用电量不超过100度,则按0.60元/度计算;(2)若每户居民每月用电量超过100度,则超过部分按0.80元/度计算(未超过部分仍按0.60元/度计算),现假设某户居民某月用电量是x(单位:度),电费为y(单位:元),则y与x的函数关系用图象表示正确的是( )
2、函数的图象一定通过(
)
A.
B.
C.
D.
3、比例函数y=-2x的大致图象是( )
4、均匀地向一个容器注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是( )
5、已知直线y=kx+b,若k+b=-5,kb=6,则该直线不经过的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6、已知一次函数过原点,则m的值为(
)
A.
B.
C.
D.不能确定
7、小明一出校门先加速行驶,然后匀速行驶一段后,在距家门不远的地方开始减速,最后停下.下面可以近似地刻画出以上情况的一副图是(
)
(
速度
速度
速度
速度
时间
时间
时间
时间
D
C
B
A
)
8.小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车.车修好后,因怕耽误上课,他比修车前加快了骑车速度匀速行驶.下面是行驶路程s(米)关于时间t(分)的函数图象,那么符合这个同学行驶情况的图象大致是(
C
).
9、如果一次函数的图象经过第一、三、四象限,那么(
)
A.,
B.,
C.,
D.,
10.函数(,)的图象不经过(
).
A.第一象限
B.第二象限
C.第三象限
D.第四象限
二、填空题
11.正比例函数的图象经过点(0,
)与(1,
).
12.一次函数的图象与x
轴的交点坐标是_______,与y
轴的交点坐标是_______.
13.已知一次函数,若它的图象经过原点,则k=_____;若y随x的增大而增大,则k__________.
14、一次函数的图象不经过第二象限,则k的取值范围是______.
15.一次函数图象经过第二、三、四象限,则m的值是__.
16.一次函数,若y随x的增大而减小,则该函数的图象经过第
象限.
三、解答题
17、已知函数y=k,当k为何值时,正比例函数y的值随x值的增大而减小?
18、已知函数y=-3x+2.
(1)求该图象与y轴的交点坐标;
(2)若点(x1,y1),(x2,y2)在函数y=-3x+2的图象上,当x1(3)将该函数的图象向下平移3个单位长度,求得到的直线所对应一次函数的表达式.
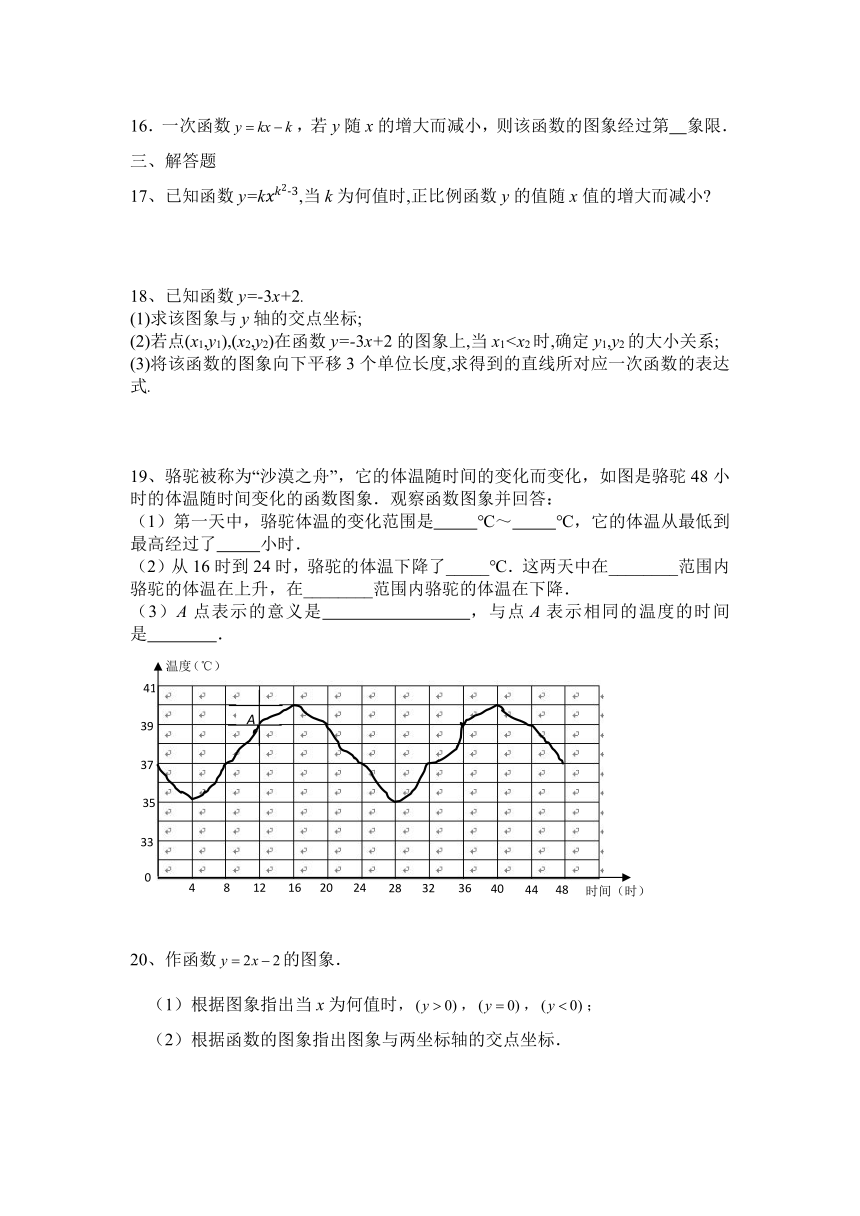
19、骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,如图是骆驼48小时的体温随时间变化的函数图象.观察函数图象并回答:
(1)第一天中,骆驼体温的变化范围是
℃~
℃,它的体温从最低到最高经过了
小时.
(2)从16时到24时,骆驼的体温下降了_____℃.这两天中在________范围内骆驼的体温在上升,在________范围内骆驼的体温在下降.
(3)A点表示的意义是
,与点A表示相同的温度的时间是
.
20、作函数的图象.
(1)根据图象指出当x为何值时,,,;
(2)根据函数的图象指出图象与两坐标轴的交点坐标.
4.3
一次函数的图象同步练习参考答案
一、选择题
1、为了节能减排,鼓励居民节约用电,某市出台了新的居民用电收费标准:(1)若每户居民每月用电量不超过100度,则按0.60元/度计算;(2)若每户居民每月用电量超过100度,则超过部分按0.80元/度计算(未超过部分仍按0.60元/度计算),现假设某户居民某月用电量是x(单位:度),电费为y(单位:元),则y与x的函数关系用图象表示正确的是( C )
2、函数的图象一定通过(
C
)
A.
B.
C.
D.
3、比例函数y=-2x的大致图象是( C )
4、均匀地向一个容器注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是( D )
5、已知直线y=kx+b,若k+b=-5,kb=6,则该直线不经过的象限是( A )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6、已知一次函数过原点,则m的值为(
C
)
A.
B.
C.
D.不能确定
7、小明一出校门先加速行驶,然后匀速行驶一段后,在距家门不远的地方开始减速,最后停下.下面可以近似地刻画出以上情况的一副图是(
C
)
(
速度
速度
速度
速度
时间
时间
时间
时间
D
C
B
A
)
8.小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车.车修好后,因怕耽误上课,他比修车前加快了骑车速度匀速行驶.下面是行驶路程s(米)关于时间t(分)的函数图象,那么符合这个同学行驶情况的图象大致是(
C
).
9、如果一次函数的图象经过第一、三、四象限,那么(
B
)
A.,
B.,
C.,
D.,
10.函数(,)的图象不经过(
A
).
A.第一象限
B.第二象限
C.第三象限
D.第四象限
二、填空题
11.正比例函数的图象经过点(0,
)与(1,
).
12.一次函数的图象与x
轴的交点坐标是_______,与y
轴的交点坐标是_______.
13.已知一次函数,若它的图象经过原点,则k=_____;若y随x的增大而增大,则k__________.
14、一次函数的图象不经过第二象限,则k的取值范围是______.
15.一次函数图象经过第二、三、四象限,则m的值是__.
16.一次函数,若y随x的增大而减小,则该函数的图象经过第
象限.
答案:
11.0,
12.(2.0),(0,-2)
13.-2
k>2
14.-115.-
16.一、二、四
三、解答题
17、已知函数y=k,当k为何值时,正比例函数y的值随x值的增大而减小?
解
∵此函数是正比例函数,∴k≠0,k2-3=1,解得k=±2.
∵此正比例函数y的值随x的增大而减小,
∴k<0,∴k=-2.
18、已知函数y=-3x+2.
(1)求该图象与y轴的交点坐标;
(2)若点(x1,y1),(x2,y2)在函数y=-3x+2的图象上,当x1(3)将该函数的图象向下平移3个单位长度,求得到的直线所对应一次函数的表达式.
解
(1)∵当x=0时,由y=-3x+2,得y=2,∴该函数图象与y轴的交点坐标是(0,2).
(2)∵函数y=-3x+2中-3<0,∴y的值随x值的增大而减小.∴当x1y2.
(3)将该函数的图象向下平移3个单位长度,得到的直线所对应一次函数的表达式是y=-3x-1.
19、骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,如图是骆驼48小时的体温随时间变化的函数图象.观察函数图象并回答:
(1)第一天中,骆驼体温的变化范围是
℃~
℃,它的体温从最低到最高经过了
小时.
(2)从16时到24时,骆驼的体温下降了_____℃.这两天中在________范围内骆驼的体温在上升,在________范围内骆驼的体温在下降.
(3)A点表示的意义是
,与点A表示相同的温度的时间是
.
答案:(1)35,40,12;(2)3,4时~16时和28时~40时,0时~4时、16时~28时和40时~48时;(3)12时骆驼的体温(39℃);20时、36时、44时.
20、作函数的图象.
(1)根据图象指出当x为何值时,,,;
(2)根据函数的图象指出图象与两坐标轴的交点坐标.
答案:(1)图略;当y>0时,2x-2>0,∴x>1,即当x>1时,y>0;当x=1时2x-2=0
即y=0;当x<1时2x-2<0即y<0;(2)当y=0时x=1,∴与x轴交点坐标为(1,0).当x=0时y=-2,∴与y轴交点坐标为(0,-2).
一次函数的图象同步练习
选择题
1、为了节能减排,鼓励居民节约用电,某市出台了新的居民用电收费标准:(1)若每户居民每月用电量不超过100度,则按0.60元/度计算;(2)若每户居民每月用电量超过100度,则超过部分按0.80元/度计算(未超过部分仍按0.60元/度计算),现假设某户居民某月用电量是x(单位:度),电费为y(单位:元),则y与x的函数关系用图象表示正确的是( )
2、函数的图象一定通过(
)
A.
B.
C.
D.
3、比例函数y=-2x的大致图象是( )
4、均匀地向一个容器注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是( )
5、已知直线y=kx+b,若k+b=-5,kb=6,则该直线不经过的象限是( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6、已知一次函数过原点,则m的值为(
)
A.
B.
C.
D.不能确定
7、小明一出校门先加速行驶,然后匀速行驶一段后,在距家门不远的地方开始减速,最后停下.下面可以近似地刻画出以上情况的一副图是(
)
(
速度
速度
速度
速度
时间
时间
时间
时间
D
C
B
A
)
8.小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车.车修好后,因怕耽误上课,他比修车前加快了骑车速度匀速行驶.下面是行驶路程s(米)关于时间t(分)的函数图象,那么符合这个同学行驶情况的图象大致是(
C
).
9、如果一次函数的图象经过第一、三、四象限,那么(
)
A.,
B.,
C.,
D.,
10.函数(,)的图象不经过(
).
A.第一象限
B.第二象限
C.第三象限
D.第四象限
二、填空题
11.正比例函数的图象经过点(0,
)与(1,
).
12.一次函数的图象与x
轴的交点坐标是_______,与y
轴的交点坐标是_______.
13.已知一次函数,若它的图象经过原点,则k=_____;若y随x的增大而增大,则k__________.
14、一次函数的图象不经过第二象限,则k的取值范围是______.
15.一次函数图象经过第二、三、四象限,则m的值是__.
16.一次函数,若y随x的增大而减小,则该函数的图象经过第
象限.
三、解答题
17、已知函数y=k,当k为何值时,正比例函数y的值随x值的增大而减小?
18、已知函数y=-3x+2.
(1)求该图象与y轴的交点坐标;
(2)若点(x1,y1),(x2,y2)在函数y=-3x+2的图象上,当x1
19、骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,如图是骆驼48小时的体温随时间变化的函数图象.观察函数图象并回答:
(1)第一天中,骆驼体温的变化范围是
℃~
℃,它的体温从最低到最高经过了
小时.
(2)从16时到24时,骆驼的体温下降了_____℃.这两天中在________范围内骆驼的体温在上升,在________范围内骆驼的体温在下降.
(3)A点表示的意义是
,与点A表示相同的温度的时间是
.
20、作函数的图象.
(1)根据图象指出当x为何值时,,,;
(2)根据函数的图象指出图象与两坐标轴的交点坐标.
4.3
一次函数的图象同步练习参考答案
一、选择题
1、为了节能减排,鼓励居民节约用电,某市出台了新的居民用电收费标准:(1)若每户居民每月用电量不超过100度,则按0.60元/度计算;(2)若每户居民每月用电量超过100度,则超过部分按0.80元/度计算(未超过部分仍按0.60元/度计算),现假设某户居民某月用电量是x(单位:度),电费为y(单位:元),则y与x的函数关系用图象表示正确的是( C )
2、函数的图象一定通过(
C
)
A.
B.
C.
D.
3、比例函数y=-2x的大致图象是( C )
4、均匀地向一个容器注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是( D )
5、已知直线y=kx+b,若k+b=-5,kb=6,则该直线不经过的象限是( A )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
6、已知一次函数过原点,则m的值为(
C
)
A.
B.
C.
D.不能确定
7、小明一出校门先加速行驶,然后匀速行驶一段后,在距家门不远的地方开始减速,最后停下.下面可以近似地刻画出以上情况的一副图是(
C
)
(
速度
速度
速度
速度
时间
时间
时间
时间
D
C
B
A
)
8.小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车.车修好后,因怕耽误上课,他比修车前加快了骑车速度匀速行驶.下面是行驶路程s(米)关于时间t(分)的函数图象,那么符合这个同学行驶情况的图象大致是(
C
).
9、如果一次函数的图象经过第一、三、四象限,那么(
B
)
A.,
B.,
C.,
D.,
10.函数(,)的图象不经过(
A
).
A.第一象限
B.第二象限
C.第三象限
D.第四象限
二、填空题
11.正比例函数的图象经过点(0,
)与(1,
).
12.一次函数的图象与x
轴的交点坐标是_______,与y
轴的交点坐标是_______.
13.已知一次函数,若它的图象经过原点,则k=_____;若y随x的增大而增大,则k__________.
14、一次函数的图象不经过第二象限,则k的取值范围是______.
15.一次函数图象经过第二、三、四象限,则m的值是__.
16.一次函数,若y随x的增大而减小,则该函数的图象经过第
象限.
答案:
11.0,
12.(2.0),(0,-2)
13.-2
k>2
14.-1
16.一、二、四
三、解答题
17、已知函数y=k,当k为何值时,正比例函数y的值随x值的增大而减小?
解
∵此函数是正比例函数,∴k≠0,k2-3=1,解得k=±2.
∵此正比例函数y的值随x的增大而减小,
∴k<0,∴k=-2.
18、已知函数y=-3x+2.
(1)求该图象与y轴的交点坐标;
(2)若点(x1,y1),(x2,y2)在函数y=-3x+2的图象上,当x1
解
(1)∵当x=0时,由y=-3x+2,得y=2,∴该函数图象与y轴的交点坐标是(0,2).
(2)∵函数y=-3x+2中-3<0,∴y的值随x值的增大而减小.∴当x1
(3)将该函数的图象向下平移3个单位长度,得到的直线所对应一次函数的表达式是y=-3x-1.
19、骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,如图是骆驼48小时的体温随时间变化的函数图象.观察函数图象并回答:
(1)第一天中,骆驼体温的变化范围是
℃~
℃,它的体温从最低到最高经过了
小时.
(2)从16时到24时,骆驼的体温下降了_____℃.这两天中在________范围内骆驼的体温在上升,在________范围内骆驼的体温在下降.
(3)A点表示的意义是
,与点A表示相同的温度的时间是
.
答案:(1)35,40,12;(2)3,4时~16时和28时~40时,0时~4时、16时~28时和40时~48时;(3)12时骆驼的体温(39℃);20时、36时、44时.
20、作函数的图象.
(1)根据图象指出当x为何值时,,,;
(2)根据函数的图象指出图象与两坐标轴的交点坐标.
答案:(1)图略;当y>0时,2x-2>0,∴x>1,即当x>1时,y>0;当x=1时2x-2=0
即y=0;当x<1时2x-2<0即y<0;(2)当y=0时x=1,∴与x轴交点坐标为(1,0).当x=0时y=-2,∴与y轴交点坐标为(0,-2).
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
