沪教版七年级数学秋季班第9讲:期中复习(一)教师版
文档属性
| 名称 | 沪教版七年级数学秋季班第9讲:期中复习(一)教师版 |
|
|
| 格式 | docx | ||
| 文件大小 | 169.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-21 00:00:00 | ||
图片预览





文档简介
期中复习一
内容分析
本讲整理了关于前面学习的整式加减和整式乘法、因式分解有有关内容的练习,以帮助同学们巩固所学.
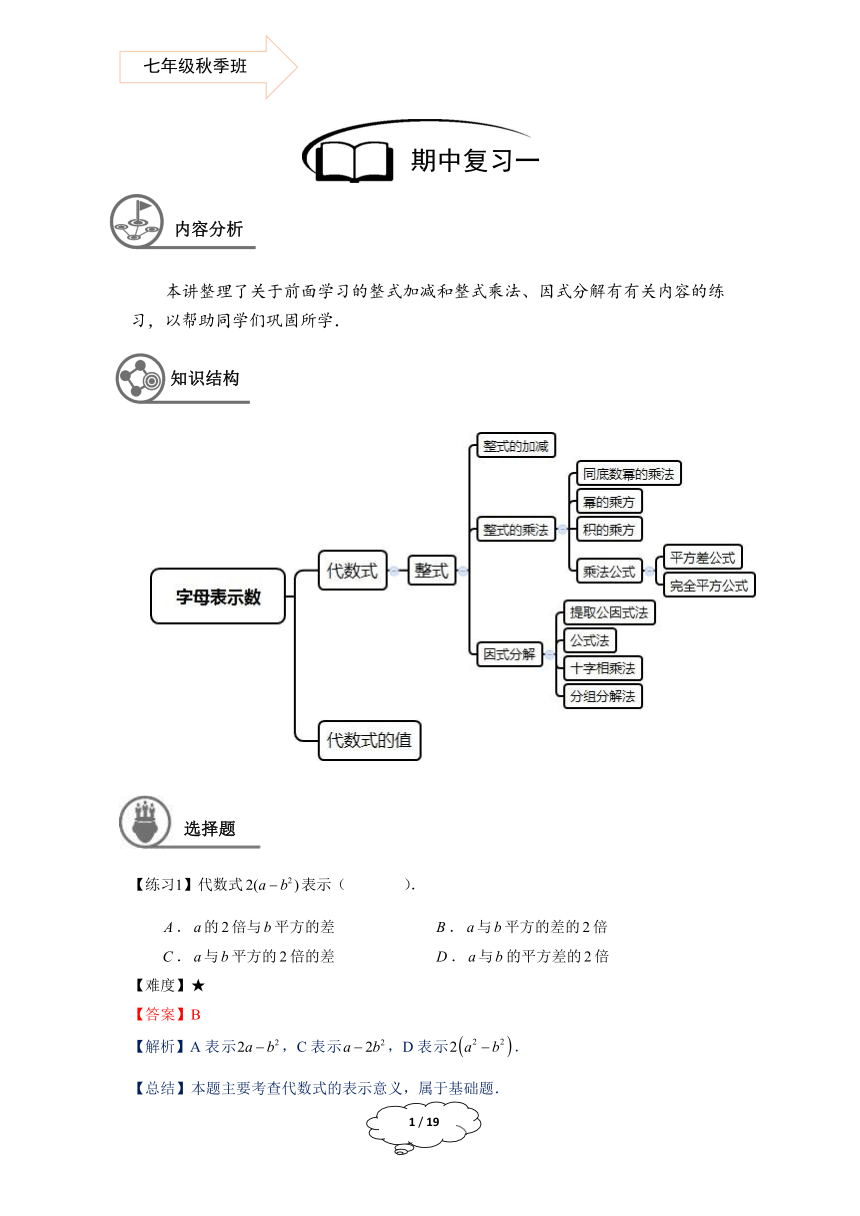
知识结构
1327843824540
选择题
【练习1】代数式2(a ? b2 ) 表示( ).
A . a 的2 倍与b 平方的差 B . a 与b 平方的差的2 倍
C . a 与b 平方的2 倍的差 D . a 与b 的平方差的2 倍
【难度】★
【答案】B
【解析】A 表示2a ? b2 ,C 表示a ? 2b2 ,D 表示2?a2 ? b2 ?.
【总结】本题主要考查代数式的表示意义,属于基础题.
【练习2】若 x 表示一个三位数, y 也表示一个三位数,小王想用 x、y 来组成一个六位数且把 x 放在 y 的左边,你认为下列表达式中( )是正确的.
A . xy B . x ? y
C .1000x ? y
D .1000y ? x
【难度】★
【答案】C
【解析】解:因为 x 在 y 的左边,y 是三位数,相当于把 x 扩大 1000 倍,所以组成的六位数是1000x ? y .
【总结】本题主要考查了代数式的表示方法,属于基础题.
【练习3】在下列式子中,属于代数式的是( ).
① 2x ? 3 ;② ?3 ;③ 1
x ? y
;④ c ? 2? r ;⑤ 1 ? x ;⑥ 2x ? 1
x
A .①②③④ B .②③④⑤ C .①②③⑤ D .③④⑤⑥
【难度】★
【答案】C
【解析】代数式包括整式、分式、根式.它不同于等式,没有等号,所以④⑥属于等式,不是代数式.
【总结】本题主要考查代数式的定义,要明白它与等式、不等式的区别.
【练习4】对于代数式① 1 abc ,② x3 ? 2xy ? y2 ,③ 1 ,④ ? 5 ,⑤ 3 x ? y ,其中判断正确
2
的是( ).
m 2 4
A .①、⑤是整式 B .①、③是三项式
C .②是二次三项式 D .②、④、⑤是一次式
【难度】★
【答案】A
【解析】①是单项式,③属于分式,所以 B 错.②是三次三项式,所以 C、D 错.故选择 A
答案.
【总结】本题主要考查代数式的相关知识点,单项式和多项式统称为整式.
【练习5】计算?x4 ?1??x2 ?1??x ?1??x ?1? 的结果是( ).
A . x8 ?1
B . x4 ?1
C . ?x ? 1?8
D . x8 ?1
【难度】★
【答案】D
【解析】原式= ?x4 ?1??x2 ?1??x2 ?1?? ?x4 ?1??x4 ?1?? ?x8 ?1?.
【总结】本题主要考查平方差公式的应用.
【练习6】若代数式3ax?7b4 与代数式?a4b2 y 是同类项,则 x y 的值是( ).
A . 9 B . ?9
【难度】★★
【答案】A
C . 4 D . ?4
【解析】解:由题意得?x ? 7 ? 4 ,解得: ?x ? ?3 ,所以 xy ? ??3?2 ? 9 .
?
?
?2 y ? 4 ? y ? 2
【总结】本题主要考查了同类项的定义,字母相同,且相同字母的指数也相同.
? 2 ?2003 2004
3
【练习7】计算? ?
? ?
A . 2
3
【难度】★★
【答案】A
?1.52002 ? ??1?
B . 3
2
2 ? 2 3 ?2002
的结果是( ).
C . ? 2
3
2
D . ? 3
2
【解析】解:原式= 3 ? ? ? ? ?1 ? .
? 3 2 ? 3
【总结】本题主要考查了积的乘方的逆运算,在计算过程中要注意奇负偶正.
【练习8】如果?m ? n?p 与?n ? m?p 相等,那么 p 应为( ).
A .奇数 B .偶数 C .整数 D .有理数
【难度】★★
【答案】B
【解析】解:要?m ? n?p 与?n ? m?p 相等,只有 p 为偶数时才能相等.
【总结】本题主要考查奇负偶正的应用.
【练习9】如果 x2 ? x ?1 ? 0 ,那么代数式 x3 ? 2x2 ? 7 的值为( ).
A . 6 B . 8 C . ?6
【难度】★★
【答案】C
D . ?8
194416992331【解析】解:
x2 ? x ?1 ? 0,? x2 ? 1? x ,代入 x3 ? 2x2 ? 7 可得
x?1? x? ? 2x2 ? 7 ? x ? x2 ? 2x2 ? 7 ? x2 ? x ? 7 ? 1? 7 ? ?6 ,故选 C.
【总结】本题主要考查将次思想以及整体代入思想的综合运用,属于必须掌握的题型.
【练习10】多项式 x2 ? kx ? 25 是一个完全平方公式,则k 的值为( ).
A . 5 B .10 C . ?5
【难度】★★
【答案】D
D . ?10
【解析】解:因为 5 和-5 的平方为 25,所以中间的可以为 10,也可以为-10.
【总结】本题主要考查了完全平方公式的灵活应用,注意两种情况的分类讨论.
【练习11】下列各式中,正确的因式分解是( ).
A . 2?a ? b? ? 3a ?b ? a? ? ?2 ? 3a??a ? b?
B . ??x ? y?2 ? ? y ? x? ? ?x ? y???x ? y ?1? C . ??x ? y?2 ? ? y ? x? ? ?? y ? x???x ? y ?1? D . ??x ? y?2 ? ? y ? x? ? ? y ? x???x ? y ?1?
【难度】★★
【答案】C
【解析】A 答案因式分解为?a ? b??2 ? 3a? ;B 答案因式分解为?x ? y???x ? y ?1? ;
D 答案因式分解为? y ? x??x ? y ?1? ;故选 C.
【总结】本题主要考查了因式分解,要注意符号的变化情况.
【练习12】下列各式由左边及右边变形不正确的有( )个.
① ?x ? y?2n ? ?? y ? x?2n ( n 为正整数);
② x2 ?10 可因式分解为?x ? 3??x ? 3? ?1;
③ x ? y ? ? y ? x?2 ? ?x ? y??1? y ? x? ;
④ a ?x ? 2? ? b?2 ? x? ? ?x ? 2??a ? b? .
A .1 B . 2 C . 3 D . 4
【难度】★★
【答案】C
【解析】① ?x ? y?2n ? ? y ? x?2n ;②在有理数的范围内无法继续分解;
③ x ? y ? ? y ? x?2 ? ?x ? y??1? x ? y? ,故选 C.
【总结】本题主要考查因式分解的相关知识点,对于提取公因式时,要注意符号的改变.
【练习13】已知?a ? b?2 ? 25 , ab ? 6 ,则a ? b ? ( ).
A .1 B . ?1
【难度】★★★
?a ? b?2
【答案】B
C . 5 D . ?5
【解析】解:
? ?a ? b?2 ? 4ab ? 25 ? 24 ? 1,?a ? b ? ?1 .
【总结】本题主要考查完全平方公式的应用,两数之差的平方等于两数之和的平方减去 4
倍的两数的乘积.
【练习14】若2x ? 4y?1 , 27y ? 3x?1 ,则 x ? y 等于( ).
A . ?5
【难度】★★★
【答案】B
B . ?3
C . ?1
D .1
194416991193【解析】解:
2x ? 4y?1 ? 22 y?2 ,? x ? 2y ? 2 ,又27y ? 3x?1 ,即33 y ? 3x?1 ,?3y ? x ?1 ,
?3y ? x ? 1 ?x ? ?4
由?x ? 2 y ? 2 ,解得: ? y ? ?1 ,所以 x ? y ? ?3 .
? ?
【总结】本题主要考查底数不同的幂相等情况,先化成底数一样,再指数对应相等.
【练习15】因式分解?a2 ? 3?2 ? 4a2 正确的是( ).
A . ?a2 ? 3 ? 2a??a2 ? 3 ? 2a?
C . ?a ? 3?2 ?a ?1?2
B . ?a ? 3?2 ?a ?1?2
D . ?a ? 3??a ? 3??a ?1??a ?1?
【难度】★★★
【答案】D
【解析】解:原式= ?a2 ? 3 ? 2a??a2 ? 3 ? 2a?? ?a ? 3??a ?1??a ? 3??a ?1? .
【总结】本题主要考查因式分解,要注意分解一定要分解到不能分解为止.
填空题
【练习16】当 a ???时, 5 ? 2(a ?1)2 的值最大?
【难度】★
【答案】-1
【解析】解:由题意可得,只有当a ? ?1时,两项的差才是最大的.
【总结】本题主要考查求最大值,某数的平方一定是非负数.
1
【练习17】当 m ???时,多项式? 3 x2 m
4
【难度】★
【答案】8
4 y2 ? x2 y ? 3 是四次多项式.
【解析】解:由题意可得: 1 m ? 4 ,?m ? 8 .
2
【总结】本题主要考查多项式的次数的规定,以某项次数最高的为多项式的次数.
【练习18】把多项式 x3 ? y2 ? 5x2 y ? 3xy2 按字母 x 升幂排列 .
【难度】★
【答案】? y2 ? 3xy2 ? 5x2 y ? x3 .
【解析】解:按字母 x 的升幂排列,即指数从小到大,所以是? y2 ? 3xy2 ? 5x2 y ? x3 .
【总结】本题主要考查了多项式的升幂排列问题,按某字母的升幂排列,就是某字母的指数要从小到大.
【练习19】已知 x ? y ? 3 ,则4?x ? y? ? 3x ? 3y ? 5 ???.
【难度】★
【答案】8
【解析】解: 4?x ? y? ? 3x ? 3y ? 5 ? 4?x ? y? ? 3?x ? y? ? 5 ? 12 ? 9 ? 5 ? 8 .
【总结】本题主要考查整体代换思想,考查学生的观察能力.
【练习20】一张长、宽分别为a 厘米、b 厘米的长方形硬纸片,四个角剪去边长均为 x 厘米的小正方形,折成一个无盖的盒子.这个盒子的底面面积是 平方厘米;当a ? 40 , b ? 30 , x ? 4 时,盒子的底面面积是 平方厘米.
【难度】★★
【答案】?a ? 2x??b ? 2x?;704 .
【解析】解:四个角均减去 x 厘米,则底面的长为?a ? 2x? 厘米,宽为?b ? 2x? 厘米, 所以底面面积为?a ? 2x??b ? 2x? 平方厘米.当a ? 40,b ? 30,x ? 4 时,
代入面积公式可得: ?40-8?? ?30-8? ? 32 ? 22 ? 704 平方厘米.
【总结】本题只要考查代数式的表示,要注意四个角均减去的话,每边就减少 2x 厘米.
【练习21】由若干盆花组成的三角形图案,每条边(包括顶点)有n ( n 为大于 1 的整数) 盆花,每个三角形图案花盆总数为 S ,则用含n 的式子表示 S 为 .
【难度】★★
【答案】 S ? 3n ? 3.
【解析】解:若每条边都只包括一个顶点的话,刚好每条边都只有一个顶点,所以每条边的花盆有?n ?1?盆,总共有三条边,所以 S ? 3n ? 3.
【总结】本题要注意封闭图形的线段和点的计算方法.
【练习22】一项工程甲独做需 m 天完成,乙独做需 n 天完成,甲、乙合作一天完成工程的
;若甲、乙两人合作需 天完成.
【难度】★★
【答案】 1 ? 1 ; mn .
m n m ? n
【解析】解:甲每一天完成的工作量是:1 ? m ? 1 ,乙每一天完成的工作量是:1 ? n ? 1 ,
m n
m n
? ?
所以甲、乙合作一天完成的工程师 1 ? 1 ;甲、乙合作需要的时间是:1 ? ? 1 ? 1 ? ? mn
m n ? ? m ? n
【总结】本题做药考查工程类问题.工作总量=工作时间? 工作效率.
【练习23】如果 a ? b ? c ,则代数式 a ? 2b ? c ? .
【难度】★★
【答案】 4 .
7
2 3 4
3a ? b ? c
【解析】解:设 a ? b ? c ? k ,则a ? 2k ,b ? 3k ,c ? 4k ,代入 a ? 2b ? c ? 2k ? 6k ? 4k ? 4 .
2 3 4 3a ? b ? c 6k ? 3k ? 4k 7
【总结】本题主要在于设未知数 k,然后进行很巧妙的转换.
【练习24】观察下列单项式: 0 , 3x2 , 8x3 ,15x4 , 24x5 ,··· ,按此规律写出第13 个单项式是 .
【难度】★★
【答案】168x13 .
【解析】解:由前面的单项式可得第 13 个单项式的系数为:
0 ? 3 ? 5 ? 7 ? 9 ?11?13 ?15 ?17 ?19 ? 21? 23 ? 25 ?168 ,次数为 13, 所以第 13 个单项式为168x13
【总结】本题属于找规律的题,主要考查学生的观察能力和分析能力.
【练习25】计算:
(1) ?b(?b)(?b)2 ? ; (2) ?a2 ? ??a?2 ? ??a?3 ? ;
(3) ?a ? b?2n ? ?b ? a?2n?1 ? .
【难度】★★
【答案】(1) b4 ;(2) a7 ;(3) ?b ? a?4n?1 .
【解析】(1)原式= ?b ? ??b?3 ? b ? b3 ? b4 ;(2)原式= ?a2 ? ??a?5 ? a2 ? a5 ? a7 ;
(3)原式= ?b ? a?2n ? ?b ? a?2n?1 ? ?b ? a?4n?1 .
【总结】本题考查了幂的运算,计算中要注意奇负偶正.
【练习26】n 为正整数,且 x2n ? 2 ,计算?3x2n ?2 ? 4?x2 ?2n ? .
【难度】★★
【答案】20
194416497791【解析】解:
x2n ? 2 ,??3x2n ?2 ? 4?x2 ?2n ? ?3x2n ?2 ? 4?x2n ?2 ? 36 ?16 ? 20 .
【总结】本题主要考查整体代换的思想的应用.
【练习27】已知5m ? 2 , 25n ? 7 ,则53m?2n ???.
【难度】★★
【答案】56
194417095921【解析】解:
5m ? 2 ,25n ? 52n ? 7 ,?53m?2n ? ?5m ?3 ? 52n ? 56 .
【总结】本题主要考查整体代换的思想的应用.
【练习28】比较大小: 255 722 .
【难度】★★
【答案】<
【解析】解: 255 ? ?25 ?11 ? 3211 ,722 ? ?72 ?11 ? 4911 ,
4135553-190833211 ? 4911 ,?255 ? 722 .
【总结】本题是幂的大小比较,要么化成底数一样,比较指数的大小;要么化成指数一样, 比较底数的大小.
【练习29】已知a ? 1 ? 3 ,则a2 ? 1 ? .
a
【难度】★★★
【答案】11.
1
a 2
? 1 ?2 1 1
【解析】解:
a ? ? 3,?? a ? ? ? 9 ,a2 ? ? 2 ? 9 ,?a2 ? ? 11 .
a ? a ? a2 a2
【总结】本题要利用完全平方公式,首尾两数互为倒数,相乘为 1.
【练习30】已知 x2 ? 4y2 ? 2x ? 4y ? 2 ? 0 ,则 xy = .
【难度】★★★
【答案】 1 .
2
【解析】解:把已知变形为: ?x2 ? 2x ?1?? ?4y2 ? 4y ?1?? 0 ,即?x ?1?2 ? ?2y ?1?2 ? 0 ,
?x ? 1 ? 0
?x ? ?1 1
?? , 解得:?
1 ,? xy ? .
?2 y ? 1 ? 0
? y ???2
?? 2
【总结】本题中包含了两个完全平方公式,要能观察出来,常数项可以合理的分解开.
1371658648123【练习31】如图,是一个有规律排列的数表,请用含n 的代数式( n 为正整数)表示数表中第 n 行第n 列的数 .
【难度】★★★
【答案】n2 ? n ?1.
【解析】解:由图观察法现,第 1 行第 1 列的数是:1;第 2 行第 2 列的数是:3;第 3 行第
3 列的数是:7;第 4 行第 4 列的数是:13;...每一个数都比前面一个数多2n ? 2 ,所以第 n 行第 n 列的数是: n2 ? n ?1.
【总结】本题是属于找规律的题目,综合性较强,主要考查学生的分析能力.
解答题
【练习32】长、宽、高依次为3a、2a、a 的长方体,把长、宽、高均增加1 后,得到新的长方体比原来长方体的体积增加多少?
【难度】★
【答案】11a2 ? 6a ?1 .
【解析】解:新的长方体的长、宽、高分别是?3a ?1?、?2a ? 1?、?a ? 1? ,所以得到的新的长
方体比原来长方体的体积增加:
?3a ?1??2a ?1??a ?1? ? 3a.2a.a ? 6a3 ?11a2 ? 6a ?1? 6a3 ? 11a2 ? 6a ?1.
【总结】本题主要考查多项式乘以多项式的运算,属于基础题.
【练习33】多项式a2 x3 ? ax2 ? 4x3 ? 2x2 ? x ?1是关于 x 的二次多项式,求a2 ? 1
a2
【难度】★
【答案】 25 .
4
a 的值.
?a2 ? 4 ? 0
?
【解析】解:因为该多项式是关于 x 的二次多项式,所以三次项的系数为 0,即?a ? 2 ? 0 ,
解得: a ? 2 ,所以a2 ? 1
a2
? a ? 4 ? 1 ? 2 ? 25 .
4 4
【总结】本题主要考查了多项式的相关知识点,不含有某项,就是某项的系数为 0.
【练习34】计算:
(1) 4a3 ? 3 ab ? b2 ? ? 5a2b ?2a2 ? 3ab ?1?;
? 2 ?
? ?
(2) ?x ?1?(x2 ? x ?1) ;
(3) ?x ?1??x ? 2? ? ?x ? 2??x ? 3? ? 2(x ? 3)(x ? 4) .
【难度】★
【答案】(1) ?4a4b ?11a3b2 ? 5a2b ;(2) x3 ? 2x2 ? 2x ?1 ;(3)12x ? 28 .
【解析】解:(1)原式= 6a4b ? 4a3b2 ?10a4b ?15a3b2 ? 5a2b ? ?4a4b ?11a3b2 ? 5a2b ;
(2)原式= x3 ? x2 ? x ? x2 ? x ? ?1 ? x3 ? 2x2 ? 2x ? ?1
(3)原式= x2 ? 3x ? 2 ? x2 ? x ? 6 ? 2x2 ?14x ? 24 ?12x ? 28
【总结】本题主要考查多项式乘多项式,属于基础题.
【练习35】已知 A ? B ? 3a2 ? 5a ?1, A ? C ? ?2a ? 3a2 ? 5 ,求a ? 2 时,求 B ? C 的值.
【难度】★
【答案】0
【解析】解: B ? C ? A ? B ? ?A ? C ? ? 3a2 ? 5a ?1? 2a ? 3a2 ? 5 ? ?3a ? 6 ,
当 a ? 2 时,代入原式=0.
【总结】本题重点在于要找出已知中的隐含条件.
【练习36】先化简,再求值:
??3ab?2 ?a2 ? ab ? b2 ?? 3ab?3a3b ? 3a2b2 ? ab3 ?,其中a ?? 3 , b ? 2 .
4 3
【难度】★★
【答案】? 2 .
3
【解析】解:原式= 9a4b2 ? 9a3b3 ? 9a2b4 ? 9a4b2 ? 9a3b3 ? 3a2b4 = ?6a2b4 , 因为a ? ? 3 ,b ? 2 ,代入原式= ?6 ? 9 ? 16 ? ? 2 .
4 3 16 81 3
【总结】本题主要考查多项式的乘法运算,先化简,再代值.
【练习37】已知a ? 1999 , b ? 1 ,求a2 ? 2b2 ? 3ab 的值.
【难度】★★
3842817366016【答案】4002000.
【解析】解: a2 ? 2b2 ? 3ab ? ?a ? b??a ? 2b? ,
a ? 1999,b ? 1,代入原式=4002000.
【总结】本题可以先因式分解,再代值求解,会比较简便.
【练习38】已知a ? b ? c ? 0 , a2 ? b2 ? c2 ? 1 ,求bc ? ca ? ab 的值.
【难度】★★
【答案】? 1 .
19441702403172
【解析】解:
a ? b ? c ? 0,??a ? b ? c?2 ? a2 ? b2 ? c2 ? 2?ab ? bc ? ac? ? 0 ,
又因为a2 ? b2 ? c2 ? 1,?1? 2?ab ? bc ? ac? ? 0 ,?ab ? bc ? ac ? ? 1 .
2
【总结】本题要熟悉三个数的和的平方公式.
【练习39】把多项式3x2 ? 4x ? 7 表示成a ?x ?1?2 ? b?x ?1? ? c 的形式,求 a ? b ? c 的值.
【难度】★★
【答案】7
【解析】解: a ?x ?1?2 ? b?x ?1? ? c ? ax2 ? ?2a ? b?x ? ?a ? b ? c? ? 3x2 ? 4x ? 7 ,
?a ? b ? c ? 7 .
【总结】解本题主要考查整式的运算,要注意对应相等.
【练习40】已知a ? b ? m , ab ? n ,用m、n 表示a4 ? 2a2b2 ? b4 .
【难度】★★
1677470348166【答案】m4 ? 4m2n ? 4n2 .
【解析】
a ? b ? m ,ab ? n ,?a4 ? 2a2b2 ? b4 ? ?a2 ? b2 ?2 ? ?m2 ? 2n?2 ? m4 ? 4m2n ? 4n2 .
【总结】本题主要考查对完全平方公式的灵活运用.
【练习41】已知m ? 2n ? 0 ,求m3 ? 2mn(m ? n) ? 4n3 ? 8 的值.
【难度】★★
【答案】?8 .
【解析】
m3 ? 2mn?m ? n? ? 4n3 ? 8 ? m3 ? 2m2n ? 2mn2 ? 4n3 ? 8
? m2 ?m ? 2n? ? 2n2 ?m ? 2n? ? 8 ? ?8 .
【总结】本题主要考查学生的分析能力和观察能力,主要采用整体代入思想进行求解.
【练习42】利用乘法公式计算:
(1) ?x2 ? 2y???x2 ? 2y?;
(2) ??2x ?1?2 ?2x ?1?2 ?16(x ? 3)2 (x ? 3)2 ;
(3) ?3x ? 2y ? 4??3x ? 2y ? 4? ? (3x ? 2y ? 4)2 ;
(4) 2002 ?1992 ?1982 ?1972 ? ···+
【难度】★★
22 ?1 .
【答案】(1) 4 y2 ? x4 ;(2) 280x2 ?1295 ;(3) ?8y2 ?12xy ? 24x ? 32 ;(4)20100.
【解析】(1)原式= ??x2 ? 2y??x2 ? 2y?? 4y2 ? x4 ;
(2)原式= ?4x2 ?1?2 ?16?x2 ? 9?2 ? ?4x2 ?1? 4x2 ? 36??4x2 ?1? 4x2 ? 36?
? ?8x2 ? 37?? 35 ? 280x2 ?1295 ;
(3)原式= ??3x ? ?2y ? 4??? ??3x ? ?2y ? 4??? ? ?3x ? 2 y ? 4?2
? 9x2 ? ?2y ? 4?2 ? 9x2 ? ?2y ? 4?2 ? 2 ? 3x ? ?2y ? 4?
? ?8y2 ?12xy ? 24x ? 32 ;
(4)原式= (200 ?199)(200 ?199) ? (198 ?197)(198 ?197) ? ??? ? (2 ?1)(2 ?1)
? 200 ?199 ?198 ?197 ? ??? ? 2 ?1
? 20100 .
【总结】本题主要考查对乘法公式的理解以及灵活运用.
【练习43】分解因式:
(1) 1 ?x ? 2 y? ? ?2 y ? x?2 ; (2) 25?x ? 2y?2 ? 4?3x ? y?2 ;
2
(3) x2 ? 2x ? a2 ? 2a ; (4) ?x ?1??x ? 4? ? 2 .
【难度】★★
【答案】(1) ?x ? 2 y?? 1 ? x ? 2 y ? ;(2) ??11x ? 8y??x ?12y? ;(3) ?x ? a??x ? a ? 2? ;
? 2 ?
? ?
(4) ?x ? 2??x ? 3?.
【解析】(1)原式= 1 ?x ? 2 y? ? ?x ? 2 y?2 ? ?x ? 2 y?? 1 ? x ? 2 y ? ;
2 ? 2 ?
? ?
(2)原式= ?5x ?10y?2 ? ?6x ? 2y?2 ? ?5x ?10y ? 6x ? 2y??5x ?10y ? 6x ? 2y?
? ?11x ? 8y???x ?12y? ? ??11x ? 8y??x ?12y? ;
(3)原式= ?x2 ? a2 ?? 2?x ? a? ? ?x ? a??x ? a? ? 2?x ? a? ? ?x ? a??x ? a ? 2?;
(4)原式= x2 ? 5x ? 4 ? 2 ? x2 ? 5x ? 6 ? ?x ? 2??x ? 3?.
【总结】本题主要考查利用合适的方法因式分解,分解式认真观察每项之间的关系.
【练习44】设 A ? 2x2 ? 3xy ? y2 ? x ? 2y , B ? 4x2 ? 6xy ? 2y2 ? y ,若 x ? 3a ? ? y ? 5?2 ? 0 ,且 B ? 2A ? a ,求 A 的值.
【难度】★★
【答案】255.
?x ? 3a ? 0
?
【解析】解:由题意可得, ? y ? 5 ? 0
?x ? 3a
?
,解得: ? y ? ?5 ,又因为 B ? 2A ? a ,
即?4x2 ? 6xy ? 2y2 ? y?? 2?2x2 ? 3xy ? y2 ? x ? 2y?? 2x ? 5y ? a .
?x ? 3a
?
由? y ? ?5
?
?2x ? 5 y ? a
?x ? ?15
?
,解得: ? y ? ?5 .
代入 A 中可得: A ? 2 ? ??15?2 ? 3? ??5?? ??15? ? ??5?2 ?15 ?10 ? 255 .
【总结】本题不但考查了代数式的运算,还考查了解三元一次方程组,还有非负数的和为零的情况.
【练习45】若 a ? ?1, b ? ?2 , c ? ?3 计算:
(1) 8an ? ??2an ?? 8an?1 ? 9an ? an?1 ;
(2) 5a2b ? ??3a2b ? ?2ab2 ? a2c?? ??7ab2 ? a2c??? .
【难度】★★
【答案】(1)当 n 为奇数时,原式= ?10 ;当 n 为偶数时,原式=10;(2)16.
494644469243【解析】解:(1)原式= 8an ? 2an ? 9an ? 8an?1 ? an?1 ? an ? 9an?1 ,所以①当 n 为奇数时,原式= ??1?n ? 9??1?n?1 ? ?1? 9 ? ?10 ;
②当 n 为偶数时,原式= ??1?n ? 9??1?n?1 ? 1? 9 ? 10 ;
a ? ?1 ,
(2)原式= 5a2b ? ??3a2b ? 2ab2 ? ac2 ? 7ab2 ? ac2 ?? ? 5a2b ? 3a2b ? 5ab2 ? 2a2b ? 5ab2 ,因为a ? ?1,b ? ?2 ,代入原式= ?4 ? 20 ? 16 .
【总结】本题要先化简,再代值,注意要分类讨论 n 的奇偶性.
【练习46】解方程(不等式)
(1) 2?x ? 3?2 ? ??x ?1?2 ? 3?x ?1??x ?1? ;
(2) 3x?3x ?1? ? ?2x ?1??2x ? 3? ? 13?x ?1??x ?1? .
【难度】★★
【答案】(1) x ? 2.2 ;(2) x ? ? 10 .
7
【解析】解:(1) 2(x2 ? 6x ? 9) ? ?x2 ? 2x ?1? 3(x2 ?1)
10x ? 22
x ? 2.2 ;
(2) 9x2 ? 3x ? 4x2 ? 4x ? 3 ? 13x2 ?13
7x ? ?10
x ? ? 10 .
7
【总结】本题主要考查了整式的计算,并利用在解方程和解不等式中,步骤一样的,先去括号,再合并同类项.
【练习47】求证: ?2x ? 3??2x ?1??x2 ?1??1 是一个完全平方式.
【难度】★★★
【答案】略.
【解析】证明:原式= (2x ? 3)(2x ?1)(x ?1)(x ?1) ?1=[(2x ? 3)(x ?1)][(2x ?1)(x ?1)] ?1
? (2x2 ? x ? 3)(2x2 ? x ?1) ?1 ? (2x2 ? x)2 ? 4(2x2 ? x) ? 4
? (2x2 ? x ? 2)2 .
所以原式是一个完全平方公式.
【总结】本题主要考查了完全平方公式的应用,同时考查了学生的观察能力和分析能力.
【练习48】求多项式2x2 ? 4xy ? 5y2 ?12y ?13 的最值.
【难度】★★★;
【答案】最小值为 1
【解析】解:原式? ?2x2 ? 4xy ? 2y2 ?? ?3y2 ?12y ?12??1 ? 2?x ? y?2 ? 3? y ? 2?2 ?1,所以原多项式有最小值,最小值为 1.
【总结】本题主要考查了对最值得理解,要么最大值,某个数减去非负数;或者最小值,非
负数加上某个数.
【练习49】计算: 2010? 20112011? 2011? 20102010 .
【难度】★★★
【答案】0.
【解析】解:原式? 2010? 2011?10001? 2011? 2010?10001 ? 0 .
【总结】本题考查了某数乘以 101,乘以 1001,乘以 10001 的规律.
【练习50】分解因式:
(1) ?2x ? 3y ? 3??2x ? 3y ? 7? ?16 ;
(2) ?a2 ? b2 ? c2 ?2 ? 4a2b2 ;
(3) x2 ? y ? z? ? y2 ?z ? x? ? z2 ?x ? y?.
? x2 y ? x2 z ? y2 z ? y2 x ? z2 ?x ? y ?
? xy ?x ? y ? ? z ? y ? x?? y ? x? ? z2 ?x ? y ?
? ?x ? y ??xy ? zy ? zx ? z2 ?
【难度】★★★
【答案】(1) ?2x ? 3y ? 5??2x ? 3y ?1? ;(2) ?a ? b ? c??a ? b ? c??a ? b ? c??a ? b ? c?;
(3) (x ? y)(x ? z)( y ? z) .
【解析】(1)原式? ?2x ? 3y?2 ? 4?2x ? 3y ?? 21 ?16 ? ?2x ? 3y?2 ? 4?2x ? 3y ?? 5
? ?2x ? 3y ? 5??2x ? 3y ?1?;
(2)原式? (a2 ? b2 ? c2 ? 2ab)(a2 ? b2 ? c2 ? 2ab)
? [(a ? b)2 ? c2 ][(a ? b)2 ? c2 ]
? (a ? b ? c)(a ? b ? c)(a ? b ? c)(a ? b ? c) ;
(3)原式? x2 y ? x2 z ? y2 z ? y2 x ? z2 x ? z2 y ? (x2 y ? z2 y) ? (x2 z ? z2 x) ? ( y2 x ? y2 z)
? y(x ? z)(x ? z) ? xz(x ? z) ? y2 (x ? z) ? (x ? z)(xy ? yz ? xz ? y2 )
? (x ? z)[ y(x ? y) ? z( y ? x)] ? (x ? z)(x ? y)( y ? z) .
【总结】本题主要考查因式分解的综合运用,要合理的利用公式法、提取公因式、分组分解法等,并且分解一定要彻底.
355484570928【练习51】读一读:式子“1? 2 ? 3 ? 4 ? 5 ? ?100 ”表示 1 开始的 100 个连续自然数的和.由
于 上 述 式 子 比 较 长 , 书 写 也 不 方 便 , 为 了 简 便 起 见 , 我 们 可 以 将
2142174106093 ? ?
100
“1? 2 ? 3 ? 4 ? 5 ? ?100 ” 表示为 n ,这里“ ”是求和符号.
n?1
2412013127041?
50
例如:1? 3 ? 5 ? 7 ? 9 ? ? 99 ,即从 1 开始的 100 以内的连续奇数的和,可表示为 (2n ?1);
n?1
?
10
又如13 ? 23 ? 33 ? 43 ? 53 ? 63 ? 73 ? 83 ? 93 ?103 可表示为 n3 .
n?1
通过对以上材料的阅读,请解答下列问题.
2497449912485
(1) 2 ? 4 ? 6 ? 8 ?10 ? ?100 (即从 2 开始的 100 以内的连续偶数的和)用求和符合可表示为 .
(2)计算?(n2 ?1)? .(填写最后的计算结果).
n?1
【难度】★★★
?
50
【答案】(1) 2n ;(2)50.
n?1
34885768063【解析】(1)由题意可得, 2 ? 4 ? 6 ? 8 ? ?100 中,每一项的表示是 2n,总共是 50 项,所
?
50
以用求和符号表示为 2n ;
n?1
5
(2)当n ? 5 时,每项的和为??n2 ?1?? 0 ? 3 ? 8 ? 15 ? 24 ? 50 .
n?1
【总结】本题属于找规律的题目,主要考查学生的分析能力和理解能力.
内容分析
本讲整理了关于前面学习的整式加减和整式乘法、因式分解有有关内容的练习,以帮助同学们巩固所学.
知识结构
1327843824540
选择题
【练习1】代数式2(a ? b2 ) 表示( ).
A . a 的2 倍与b 平方的差 B . a 与b 平方的差的2 倍
C . a 与b 平方的2 倍的差 D . a 与b 的平方差的2 倍
【难度】★
【答案】B
【解析】A 表示2a ? b2 ,C 表示a ? 2b2 ,D 表示2?a2 ? b2 ?.
【总结】本题主要考查代数式的表示意义,属于基础题.
【练习2】若 x 表示一个三位数, y 也表示一个三位数,小王想用 x、y 来组成一个六位数且把 x 放在 y 的左边,你认为下列表达式中( )是正确的.
A . xy B . x ? y
C .1000x ? y
D .1000y ? x
【难度】★
【答案】C
【解析】解:因为 x 在 y 的左边,y 是三位数,相当于把 x 扩大 1000 倍,所以组成的六位数是1000x ? y .
【总结】本题主要考查了代数式的表示方法,属于基础题.
【练习3】在下列式子中,属于代数式的是( ).
① 2x ? 3 ;② ?3 ;③ 1
x ? y
;④ c ? 2? r ;⑤ 1 ? x ;⑥ 2x ? 1
x
A .①②③④ B .②③④⑤ C .①②③⑤ D .③④⑤⑥
【难度】★
【答案】C
【解析】代数式包括整式、分式、根式.它不同于等式,没有等号,所以④⑥属于等式,不是代数式.
【总结】本题主要考查代数式的定义,要明白它与等式、不等式的区别.
【练习4】对于代数式① 1 abc ,② x3 ? 2xy ? y2 ,③ 1 ,④ ? 5 ,⑤ 3 x ? y ,其中判断正确
2
的是( ).
m 2 4
A .①、⑤是整式 B .①、③是三项式
C .②是二次三项式 D .②、④、⑤是一次式
【难度】★
【答案】A
【解析】①是单项式,③属于分式,所以 B 错.②是三次三项式,所以 C、D 错.故选择 A
答案.
【总结】本题主要考查代数式的相关知识点,单项式和多项式统称为整式.
【练习5】计算?x4 ?1??x2 ?1??x ?1??x ?1? 的结果是( ).
A . x8 ?1
B . x4 ?1
C . ?x ? 1?8
D . x8 ?1
【难度】★
【答案】D
【解析】原式= ?x4 ?1??x2 ?1??x2 ?1?? ?x4 ?1??x4 ?1?? ?x8 ?1?.
【总结】本题主要考查平方差公式的应用.
【练习6】若代数式3ax?7b4 与代数式?a4b2 y 是同类项,则 x y 的值是( ).
A . 9 B . ?9
【难度】★★
【答案】A
C . 4 D . ?4
【解析】解:由题意得?x ? 7 ? 4 ,解得: ?x ? ?3 ,所以 xy ? ??3?2 ? 9 .
?
?
?2 y ? 4 ? y ? 2
【总结】本题主要考查了同类项的定义,字母相同,且相同字母的指数也相同.
? 2 ?2003 2004
3
【练习7】计算? ?
? ?
A . 2
3
【难度】★★
【答案】A
?1.52002 ? ??1?
B . 3
2
2 ? 2 3 ?2002
的结果是( ).
C . ? 2
3
2
D . ? 3
2
【解析】解:原式= 3 ? ? ? ? ?1 ? .
? 3 2 ? 3
【总结】本题主要考查了积的乘方的逆运算,在计算过程中要注意奇负偶正.
【练习8】如果?m ? n?p 与?n ? m?p 相等,那么 p 应为( ).
A .奇数 B .偶数 C .整数 D .有理数
【难度】★★
【答案】B
【解析】解:要?m ? n?p 与?n ? m?p 相等,只有 p 为偶数时才能相等.
【总结】本题主要考查奇负偶正的应用.
【练习9】如果 x2 ? x ?1 ? 0 ,那么代数式 x3 ? 2x2 ? 7 的值为( ).
A . 6 B . 8 C . ?6
【难度】★★
【答案】C
D . ?8
194416992331【解析】解:
x2 ? x ?1 ? 0,? x2 ? 1? x ,代入 x3 ? 2x2 ? 7 可得
x?1? x? ? 2x2 ? 7 ? x ? x2 ? 2x2 ? 7 ? x2 ? x ? 7 ? 1? 7 ? ?6 ,故选 C.
【总结】本题主要考查将次思想以及整体代入思想的综合运用,属于必须掌握的题型.
【练习10】多项式 x2 ? kx ? 25 是一个完全平方公式,则k 的值为( ).
A . 5 B .10 C . ?5
【难度】★★
【答案】D
D . ?10
【解析】解:因为 5 和-5 的平方为 25,所以中间的可以为 10,也可以为-10.
【总结】本题主要考查了完全平方公式的灵活应用,注意两种情况的分类讨论.
【练习11】下列各式中,正确的因式分解是( ).
A . 2?a ? b? ? 3a ?b ? a? ? ?2 ? 3a??a ? b?
B . ??x ? y?2 ? ? y ? x? ? ?x ? y???x ? y ?1? C . ??x ? y?2 ? ? y ? x? ? ?? y ? x???x ? y ?1? D . ??x ? y?2 ? ? y ? x? ? ? y ? x???x ? y ?1?
【难度】★★
【答案】C
【解析】A 答案因式分解为?a ? b??2 ? 3a? ;B 答案因式分解为?x ? y???x ? y ?1? ;
D 答案因式分解为? y ? x??x ? y ?1? ;故选 C.
【总结】本题主要考查了因式分解,要注意符号的变化情况.
【练习12】下列各式由左边及右边变形不正确的有( )个.
① ?x ? y?2n ? ?? y ? x?2n ( n 为正整数);
② x2 ?10 可因式分解为?x ? 3??x ? 3? ?1;
③ x ? y ? ? y ? x?2 ? ?x ? y??1? y ? x? ;
④ a ?x ? 2? ? b?2 ? x? ? ?x ? 2??a ? b? .
A .1 B . 2 C . 3 D . 4
【难度】★★
【答案】C
【解析】① ?x ? y?2n ? ? y ? x?2n ;②在有理数的范围内无法继续分解;
③ x ? y ? ? y ? x?2 ? ?x ? y??1? x ? y? ,故选 C.
【总结】本题主要考查因式分解的相关知识点,对于提取公因式时,要注意符号的改变.
【练习13】已知?a ? b?2 ? 25 , ab ? 6 ,则a ? b ? ( ).
A .1 B . ?1
【难度】★★★
?a ? b?2
【答案】B
C . 5 D . ?5
【解析】解:
? ?a ? b?2 ? 4ab ? 25 ? 24 ? 1,?a ? b ? ?1 .
【总结】本题主要考查完全平方公式的应用,两数之差的平方等于两数之和的平方减去 4
倍的两数的乘积.
【练习14】若2x ? 4y?1 , 27y ? 3x?1 ,则 x ? y 等于( ).
A . ?5
【难度】★★★
【答案】B
B . ?3
C . ?1
D .1
194416991193【解析】解:
2x ? 4y?1 ? 22 y?2 ,? x ? 2y ? 2 ,又27y ? 3x?1 ,即33 y ? 3x?1 ,?3y ? x ?1 ,
?3y ? x ? 1 ?x ? ?4
由?x ? 2 y ? 2 ,解得: ? y ? ?1 ,所以 x ? y ? ?3 .
? ?
【总结】本题主要考查底数不同的幂相等情况,先化成底数一样,再指数对应相等.
【练习15】因式分解?a2 ? 3?2 ? 4a2 正确的是( ).
A . ?a2 ? 3 ? 2a??a2 ? 3 ? 2a?
C . ?a ? 3?2 ?a ?1?2
B . ?a ? 3?2 ?a ?1?2
D . ?a ? 3??a ? 3??a ?1??a ?1?
【难度】★★★
【答案】D
【解析】解:原式= ?a2 ? 3 ? 2a??a2 ? 3 ? 2a?? ?a ? 3??a ?1??a ? 3??a ?1? .
【总结】本题主要考查因式分解,要注意分解一定要分解到不能分解为止.
填空题
【练习16】当 a ???时, 5 ? 2(a ?1)2 的值最大?
【难度】★
【答案】-1
【解析】解:由题意可得,只有当a ? ?1时,两项的差才是最大的.
【总结】本题主要考查求最大值,某数的平方一定是非负数.
1
【练习17】当 m ???时,多项式? 3 x2 m
4
【难度】★
【答案】8
4 y2 ? x2 y ? 3 是四次多项式.
【解析】解:由题意可得: 1 m ? 4 ,?m ? 8 .
2
【总结】本题主要考查多项式的次数的规定,以某项次数最高的为多项式的次数.
【练习18】把多项式 x3 ? y2 ? 5x2 y ? 3xy2 按字母 x 升幂排列 .
【难度】★
【答案】? y2 ? 3xy2 ? 5x2 y ? x3 .
【解析】解:按字母 x 的升幂排列,即指数从小到大,所以是? y2 ? 3xy2 ? 5x2 y ? x3 .
【总结】本题主要考查了多项式的升幂排列问题,按某字母的升幂排列,就是某字母的指数要从小到大.
【练习19】已知 x ? y ? 3 ,则4?x ? y? ? 3x ? 3y ? 5 ???.
【难度】★
【答案】8
【解析】解: 4?x ? y? ? 3x ? 3y ? 5 ? 4?x ? y? ? 3?x ? y? ? 5 ? 12 ? 9 ? 5 ? 8 .
【总结】本题主要考查整体代换思想,考查学生的观察能力.
【练习20】一张长、宽分别为a 厘米、b 厘米的长方形硬纸片,四个角剪去边长均为 x 厘米的小正方形,折成一个无盖的盒子.这个盒子的底面面积是 平方厘米;当a ? 40 , b ? 30 , x ? 4 时,盒子的底面面积是 平方厘米.
【难度】★★
【答案】?a ? 2x??b ? 2x?;704 .
【解析】解:四个角均减去 x 厘米,则底面的长为?a ? 2x? 厘米,宽为?b ? 2x? 厘米, 所以底面面积为?a ? 2x??b ? 2x? 平方厘米.当a ? 40,b ? 30,x ? 4 时,
代入面积公式可得: ?40-8?? ?30-8? ? 32 ? 22 ? 704 平方厘米.
【总结】本题只要考查代数式的表示,要注意四个角均减去的话,每边就减少 2x 厘米.
【练习21】由若干盆花组成的三角形图案,每条边(包括顶点)有n ( n 为大于 1 的整数) 盆花,每个三角形图案花盆总数为 S ,则用含n 的式子表示 S 为 .
【难度】★★
【答案】 S ? 3n ? 3.
【解析】解:若每条边都只包括一个顶点的话,刚好每条边都只有一个顶点,所以每条边的花盆有?n ?1?盆,总共有三条边,所以 S ? 3n ? 3.
【总结】本题要注意封闭图形的线段和点的计算方法.
【练习22】一项工程甲独做需 m 天完成,乙独做需 n 天完成,甲、乙合作一天完成工程的
;若甲、乙两人合作需 天完成.
【难度】★★
【答案】 1 ? 1 ; mn .
m n m ? n
【解析】解:甲每一天完成的工作量是:1 ? m ? 1 ,乙每一天完成的工作量是:1 ? n ? 1 ,
m n
m n
? ?
所以甲、乙合作一天完成的工程师 1 ? 1 ;甲、乙合作需要的时间是:1 ? ? 1 ? 1 ? ? mn
m n ? ? m ? n
【总结】本题做药考查工程类问题.工作总量=工作时间? 工作效率.
【练习23】如果 a ? b ? c ,则代数式 a ? 2b ? c ? .
【难度】★★
【答案】 4 .
7
2 3 4
3a ? b ? c
【解析】解:设 a ? b ? c ? k ,则a ? 2k ,b ? 3k ,c ? 4k ,代入 a ? 2b ? c ? 2k ? 6k ? 4k ? 4 .
2 3 4 3a ? b ? c 6k ? 3k ? 4k 7
【总结】本题主要在于设未知数 k,然后进行很巧妙的转换.
【练习24】观察下列单项式: 0 , 3x2 , 8x3 ,15x4 , 24x5 ,··· ,按此规律写出第13 个单项式是 .
【难度】★★
【答案】168x13 .
【解析】解:由前面的单项式可得第 13 个单项式的系数为:
0 ? 3 ? 5 ? 7 ? 9 ?11?13 ?15 ?17 ?19 ? 21? 23 ? 25 ?168 ,次数为 13, 所以第 13 个单项式为168x13
【总结】本题属于找规律的题,主要考查学生的观察能力和分析能力.
【练习25】计算:
(1) ?b(?b)(?b)2 ? ; (2) ?a2 ? ??a?2 ? ??a?3 ? ;
(3) ?a ? b?2n ? ?b ? a?2n?1 ? .
【难度】★★
【答案】(1) b4 ;(2) a7 ;(3) ?b ? a?4n?1 .
【解析】(1)原式= ?b ? ??b?3 ? b ? b3 ? b4 ;(2)原式= ?a2 ? ??a?5 ? a2 ? a5 ? a7 ;
(3)原式= ?b ? a?2n ? ?b ? a?2n?1 ? ?b ? a?4n?1 .
【总结】本题考查了幂的运算,计算中要注意奇负偶正.
【练习26】n 为正整数,且 x2n ? 2 ,计算?3x2n ?2 ? 4?x2 ?2n ? .
【难度】★★
【答案】20
194416497791【解析】解:
x2n ? 2 ,??3x2n ?2 ? 4?x2 ?2n ? ?3x2n ?2 ? 4?x2n ?2 ? 36 ?16 ? 20 .
【总结】本题主要考查整体代换的思想的应用.
【练习27】已知5m ? 2 , 25n ? 7 ,则53m?2n ???.
【难度】★★
【答案】56
194417095921【解析】解:
5m ? 2 ,25n ? 52n ? 7 ,?53m?2n ? ?5m ?3 ? 52n ? 56 .
【总结】本题主要考查整体代换的思想的应用.
【练习28】比较大小: 255 722 .
【难度】★★
【答案】<
【解析】解: 255 ? ?25 ?11 ? 3211 ,722 ? ?72 ?11 ? 4911 ,
4135553-190833211 ? 4911 ,?255 ? 722 .
【总结】本题是幂的大小比较,要么化成底数一样,比较指数的大小;要么化成指数一样, 比较底数的大小.
【练习29】已知a ? 1 ? 3 ,则a2 ? 1 ? .
a
【难度】★★★
【答案】11.
1
a 2
? 1 ?2 1 1
【解析】解:
a ? ? 3,?? a ? ? ? 9 ,a2 ? ? 2 ? 9 ,?a2 ? ? 11 .
a ? a ? a2 a2
【总结】本题要利用完全平方公式,首尾两数互为倒数,相乘为 1.
【练习30】已知 x2 ? 4y2 ? 2x ? 4y ? 2 ? 0 ,则 xy = .
【难度】★★★
【答案】 1 .
2
【解析】解:把已知变形为: ?x2 ? 2x ?1?? ?4y2 ? 4y ?1?? 0 ,即?x ?1?2 ? ?2y ?1?2 ? 0 ,
?x ? 1 ? 0
?x ? ?1 1
?? , 解得:?
1 ,? xy ? .
?2 y ? 1 ? 0
? y ???2
?? 2
【总结】本题中包含了两个完全平方公式,要能观察出来,常数项可以合理的分解开.
1371658648123【练习31】如图,是一个有规律排列的数表,请用含n 的代数式( n 为正整数)表示数表中第 n 行第n 列的数 .
【难度】★★★
【答案】n2 ? n ?1.
【解析】解:由图观察法现,第 1 行第 1 列的数是:1;第 2 行第 2 列的数是:3;第 3 行第
3 列的数是:7;第 4 行第 4 列的数是:13;...每一个数都比前面一个数多2n ? 2 ,所以第 n 行第 n 列的数是: n2 ? n ?1.
【总结】本题是属于找规律的题目,综合性较强,主要考查学生的分析能力.
解答题
【练习32】长、宽、高依次为3a、2a、a 的长方体,把长、宽、高均增加1 后,得到新的长方体比原来长方体的体积增加多少?
【难度】★
【答案】11a2 ? 6a ?1 .
【解析】解:新的长方体的长、宽、高分别是?3a ?1?、?2a ? 1?、?a ? 1? ,所以得到的新的长
方体比原来长方体的体积增加:
?3a ?1??2a ?1??a ?1? ? 3a.2a.a ? 6a3 ?11a2 ? 6a ?1? 6a3 ? 11a2 ? 6a ?1.
【总结】本题主要考查多项式乘以多项式的运算,属于基础题.
【练习33】多项式a2 x3 ? ax2 ? 4x3 ? 2x2 ? x ?1是关于 x 的二次多项式,求a2 ? 1
a2
【难度】★
【答案】 25 .
4
a 的值.
?a2 ? 4 ? 0
?
【解析】解:因为该多项式是关于 x 的二次多项式,所以三次项的系数为 0,即?a ? 2 ? 0 ,
解得: a ? 2 ,所以a2 ? 1
a2
? a ? 4 ? 1 ? 2 ? 25 .
4 4
【总结】本题主要考查了多项式的相关知识点,不含有某项,就是某项的系数为 0.
【练习34】计算:
(1) 4a3 ? 3 ab ? b2 ? ? 5a2b ?2a2 ? 3ab ?1?;
? 2 ?
? ?
(2) ?x ?1?(x2 ? x ?1) ;
(3) ?x ?1??x ? 2? ? ?x ? 2??x ? 3? ? 2(x ? 3)(x ? 4) .
【难度】★
【答案】(1) ?4a4b ?11a3b2 ? 5a2b ;(2) x3 ? 2x2 ? 2x ?1 ;(3)12x ? 28 .
【解析】解:(1)原式= 6a4b ? 4a3b2 ?10a4b ?15a3b2 ? 5a2b ? ?4a4b ?11a3b2 ? 5a2b ;
(2)原式= x3 ? x2 ? x ? x2 ? x ? ?1 ? x3 ? 2x2 ? 2x ? ?1
(3)原式= x2 ? 3x ? 2 ? x2 ? x ? 6 ? 2x2 ?14x ? 24 ?12x ? 28
【总结】本题主要考查多项式乘多项式,属于基础题.
【练习35】已知 A ? B ? 3a2 ? 5a ?1, A ? C ? ?2a ? 3a2 ? 5 ,求a ? 2 时,求 B ? C 的值.
【难度】★
【答案】0
【解析】解: B ? C ? A ? B ? ?A ? C ? ? 3a2 ? 5a ?1? 2a ? 3a2 ? 5 ? ?3a ? 6 ,
当 a ? 2 时,代入原式=0.
【总结】本题重点在于要找出已知中的隐含条件.
【练习36】先化简,再求值:
??3ab?2 ?a2 ? ab ? b2 ?? 3ab?3a3b ? 3a2b2 ? ab3 ?,其中a ?? 3 , b ? 2 .
4 3
【难度】★★
【答案】? 2 .
3
【解析】解:原式= 9a4b2 ? 9a3b3 ? 9a2b4 ? 9a4b2 ? 9a3b3 ? 3a2b4 = ?6a2b4 , 因为a ? ? 3 ,b ? 2 ,代入原式= ?6 ? 9 ? 16 ? ? 2 .
4 3 16 81 3
【总结】本题主要考查多项式的乘法运算,先化简,再代值.
【练习37】已知a ? 1999 , b ? 1 ,求a2 ? 2b2 ? 3ab 的值.
【难度】★★
3842817366016【答案】4002000.
【解析】解: a2 ? 2b2 ? 3ab ? ?a ? b??a ? 2b? ,
a ? 1999,b ? 1,代入原式=4002000.
【总结】本题可以先因式分解,再代值求解,会比较简便.
【练习38】已知a ? b ? c ? 0 , a2 ? b2 ? c2 ? 1 ,求bc ? ca ? ab 的值.
【难度】★★
【答案】? 1 .
19441702403172
【解析】解:
a ? b ? c ? 0,??a ? b ? c?2 ? a2 ? b2 ? c2 ? 2?ab ? bc ? ac? ? 0 ,
又因为a2 ? b2 ? c2 ? 1,?1? 2?ab ? bc ? ac? ? 0 ,?ab ? bc ? ac ? ? 1 .
2
【总结】本题要熟悉三个数的和的平方公式.
【练习39】把多项式3x2 ? 4x ? 7 表示成a ?x ?1?2 ? b?x ?1? ? c 的形式,求 a ? b ? c 的值.
【难度】★★
【答案】7
【解析】解: a ?x ?1?2 ? b?x ?1? ? c ? ax2 ? ?2a ? b?x ? ?a ? b ? c? ? 3x2 ? 4x ? 7 ,
?a ? b ? c ? 7 .
【总结】解本题主要考查整式的运算,要注意对应相等.
【练习40】已知a ? b ? m , ab ? n ,用m、n 表示a4 ? 2a2b2 ? b4 .
【难度】★★
1677470348166【答案】m4 ? 4m2n ? 4n2 .
【解析】
a ? b ? m ,ab ? n ,?a4 ? 2a2b2 ? b4 ? ?a2 ? b2 ?2 ? ?m2 ? 2n?2 ? m4 ? 4m2n ? 4n2 .
【总结】本题主要考查对完全平方公式的灵活运用.
【练习41】已知m ? 2n ? 0 ,求m3 ? 2mn(m ? n) ? 4n3 ? 8 的值.
【难度】★★
【答案】?8 .
【解析】
m3 ? 2mn?m ? n? ? 4n3 ? 8 ? m3 ? 2m2n ? 2mn2 ? 4n3 ? 8
? m2 ?m ? 2n? ? 2n2 ?m ? 2n? ? 8 ? ?8 .
【总结】本题主要考查学生的分析能力和观察能力,主要采用整体代入思想进行求解.
【练习42】利用乘法公式计算:
(1) ?x2 ? 2y???x2 ? 2y?;
(2) ??2x ?1?2 ?2x ?1?2 ?16(x ? 3)2 (x ? 3)2 ;
(3) ?3x ? 2y ? 4??3x ? 2y ? 4? ? (3x ? 2y ? 4)2 ;
(4) 2002 ?1992 ?1982 ?1972 ? ···+
【难度】★★
22 ?1 .
【答案】(1) 4 y2 ? x4 ;(2) 280x2 ?1295 ;(3) ?8y2 ?12xy ? 24x ? 32 ;(4)20100.
【解析】(1)原式= ??x2 ? 2y??x2 ? 2y?? 4y2 ? x4 ;
(2)原式= ?4x2 ?1?2 ?16?x2 ? 9?2 ? ?4x2 ?1? 4x2 ? 36??4x2 ?1? 4x2 ? 36?
? ?8x2 ? 37?? 35 ? 280x2 ?1295 ;
(3)原式= ??3x ? ?2y ? 4??? ??3x ? ?2y ? 4??? ? ?3x ? 2 y ? 4?2
? 9x2 ? ?2y ? 4?2 ? 9x2 ? ?2y ? 4?2 ? 2 ? 3x ? ?2y ? 4?
? ?8y2 ?12xy ? 24x ? 32 ;
(4)原式= (200 ?199)(200 ?199) ? (198 ?197)(198 ?197) ? ??? ? (2 ?1)(2 ?1)
? 200 ?199 ?198 ?197 ? ??? ? 2 ?1
? 20100 .
【总结】本题主要考查对乘法公式的理解以及灵活运用.
【练习43】分解因式:
(1) 1 ?x ? 2 y? ? ?2 y ? x?2 ; (2) 25?x ? 2y?2 ? 4?3x ? y?2 ;
2
(3) x2 ? 2x ? a2 ? 2a ; (4) ?x ?1??x ? 4? ? 2 .
【难度】★★
【答案】(1) ?x ? 2 y?? 1 ? x ? 2 y ? ;(2) ??11x ? 8y??x ?12y? ;(3) ?x ? a??x ? a ? 2? ;
? 2 ?
? ?
(4) ?x ? 2??x ? 3?.
【解析】(1)原式= 1 ?x ? 2 y? ? ?x ? 2 y?2 ? ?x ? 2 y?? 1 ? x ? 2 y ? ;
2 ? 2 ?
? ?
(2)原式= ?5x ?10y?2 ? ?6x ? 2y?2 ? ?5x ?10y ? 6x ? 2y??5x ?10y ? 6x ? 2y?
? ?11x ? 8y???x ?12y? ? ??11x ? 8y??x ?12y? ;
(3)原式= ?x2 ? a2 ?? 2?x ? a? ? ?x ? a??x ? a? ? 2?x ? a? ? ?x ? a??x ? a ? 2?;
(4)原式= x2 ? 5x ? 4 ? 2 ? x2 ? 5x ? 6 ? ?x ? 2??x ? 3?.
【总结】本题主要考查利用合适的方法因式分解,分解式认真观察每项之间的关系.
【练习44】设 A ? 2x2 ? 3xy ? y2 ? x ? 2y , B ? 4x2 ? 6xy ? 2y2 ? y ,若 x ? 3a ? ? y ? 5?2 ? 0 ,且 B ? 2A ? a ,求 A 的值.
【难度】★★
【答案】255.
?x ? 3a ? 0
?
【解析】解:由题意可得, ? y ? 5 ? 0
?x ? 3a
?
,解得: ? y ? ?5 ,又因为 B ? 2A ? a ,
即?4x2 ? 6xy ? 2y2 ? y?? 2?2x2 ? 3xy ? y2 ? x ? 2y?? 2x ? 5y ? a .
?x ? 3a
?
由? y ? ?5
?
?2x ? 5 y ? a
?x ? ?15
?
,解得: ? y ? ?5 .
代入 A 中可得: A ? 2 ? ??15?2 ? 3? ??5?? ??15? ? ??5?2 ?15 ?10 ? 255 .
【总结】本题不但考查了代数式的运算,还考查了解三元一次方程组,还有非负数的和为零的情况.
【练习45】若 a ? ?1, b ? ?2 , c ? ?3 计算:
(1) 8an ? ??2an ?? 8an?1 ? 9an ? an?1 ;
(2) 5a2b ? ??3a2b ? ?2ab2 ? a2c?? ??7ab2 ? a2c??? .
【难度】★★
【答案】(1)当 n 为奇数时,原式= ?10 ;当 n 为偶数时,原式=10;(2)16.
494644469243【解析】解:(1)原式= 8an ? 2an ? 9an ? 8an?1 ? an?1 ? an ? 9an?1 ,所以①当 n 为奇数时,原式= ??1?n ? 9??1?n?1 ? ?1? 9 ? ?10 ;
②当 n 为偶数时,原式= ??1?n ? 9??1?n?1 ? 1? 9 ? 10 ;
a ? ?1 ,
(2)原式= 5a2b ? ??3a2b ? 2ab2 ? ac2 ? 7ab2 ? ac2 ?? ? 5a2b ? 3a2b ? 5ab2 ? 2a2b ? 5ab2 ,因为a ? ?1,b ? ?2 ,代入原式= ?4 ? 20 ? 16 .
【总结】本题要先化简,再代值,注意要分类讨论 n 的奇偶性.
【练习46】解方程(不等式)
(1) 2?x ? 3?2 ? ??x ?1?2 ? 3?x ?1??x ?1? ;
(2) 3x?3x ?1? ? ?2x ?1??2x ? 3? ? 13?x ?1??x ?1? .
【难度】★★
【答案】(1) x ? 2.2 ;(2) x ? ? 10 .
7
【解析】解:(1) 2(x2 ? 6x ? 9) ? ?x2 ? 2x ?1? 3(x2 ?1)
10x ? 22
x ? 2.2 ;
(2) 9x2 ? 3x ? 4x2 ? 4x ? 3 ? 13x2 ?13
7x ? ?10
x ? ? 10 .
7
【总结】本题主要考查了整式的计算,并利用在解方程和解不等式中,步骤一样的,先去括号,再合并同类项.
【练习47】求证: ?2x ? 3??2x ?1??x2 ?1??1 是一个完全平方式.
【难度】★★★
【答案】略.
【解析】证明:原式= (2x ? 3)(2x ?1)(x ?1)(x ?1) ?1=[(2x ? 3)(x ?1)][(2x ?1)(x ?1)] ?1
? (2x2 ? x ? 3)(2x2 ? x ?1) ?1 ? (2x2 ? x)2 ? 4(2x2 ? x) ? 4
? (2x2 ? x ? 2)2 .
所以原式是一个完全平方公式.
【总结】本题主要考查了完全平方公式的应用,同时考查了学生的观察能力和分析能力.
【练习48】求多项式2x2 ? 4xy ? 5y2 ?12y ?13 的最值.
【难度】★★★;
【答案】最小值为 1
【解析】解:原式? ?2x2 ? 4xy ? 2y2 ?? ?3y2 ?12y ?12??1 ? 2?x ? y?2 ? 3? y ? 2?2 ?1,所以原多项式有最小值,最小值为 1.
【总结】本题主要考查了对最值得理解,要么最大值,某个数减去非负数;或者最小值,非
负数加上某个数.
【练习49】计算: 2010? 20112011? 2011? 20102010 .
【难度】★★★
【答案】0.
【解析】解:原式? 2010? 2011?10001? 2011? 2010?10001 ? 0 .
【总结】本题考查了某数乘以 101,乘以 1001,乘以 10001 的规律.
【练习50】分解因式:
(1) ?2x ? 3y ? 3??2x ? 3y ? 7? ?16 ;
(2) ?a2 ? b2 ? c2 ?2 ? 4a2b2 ;
(3) x2 ? y ? z? ? y2 ?z ? x? ? z2 ?x ? y?.
? x2 y ? x2 z ? y2 z ? y2 x ? z2 ?x ? y ?
? xy ?x ? y ? ? z ? y ? x?? y ? x? ? z2 ?x ? y ?
? ?x ? y ??xy ? zy ? zx ? z2 ?
【难度】★★★
【答案】(1) ?2x ? 3y ? 5??2x ? 3y ?1? ;(2) ?a ? b ? c??a ? b ? c??a ? b ? c??a ? b ? c?;
(3) (x ? y)(x ? z)( y ? z) .
【解析】(1)原式? ?2x ? 3y?2 ? 4?2x ? 3y ?? 21 ?16 ? ?2x ? 3y?2 ? 4?2x ? 3y ?? 5
? ?2x ? 3y ? 5??2x ? 3y ?1?;
(2)原式? (a2 ? b2 ? c2 ? 2ab)(a2 ? b2 ? c2 ? 2ab)
? [(a ? b)2 ? c2 ][(a ? b)2 ? c2 ]
? (a ? b ? c)(a ? b ? c)(a ? b ? c)(a ? b ? c) ;
(3)原式? x2 y ? x2 z ? y2 z ? y2 x ? z2 x ? z2 y ? (x2 y ? z2 y) ? (x2 z ? z2 x) ? ( y2 x ? y2 z)
? y(x ? z)(x ? z) ? xz(x ? z) ? y2 (x ? z) ? (x ? z)(xy ? yz ? xz ? y2 )
? (x ? z)[ y(x ? y) ? z( y ? x)] ? (x ? z)(x ? y)( y ? z) .
【总结】本题主要考查因式分解的综合运用,要合理的利用公式法、提取公因式、分组分解法等,并且分解一定要彻底.
355484570928【练习51】读一读:式子“1? 2 ? 3 ? 4 ? 5 ? ?100 ”表示 1 开始的 100 个连续自然数的和.由
于 上 述 式 子 比 较 长 , 书 写 也 不 方 便 , 为 了 简 便 起 见 , 我 们 可 以 将
2142174106093 ? ?
100
“1? 2 ? 3 ? 4 ? 5 ? ?100 ” 表示为 n ,这里“ ”是求和符号.
n?1
2412013127041?
50
例如:1? 3 ? 5 ? 7 ? 9 ? ? 99 ,即从 1 开始的 100 以内的连续奇数的和,可表示为 (2n ?1);
n?1
?
10
又如13 ? 23 ? 33 ? 43 ? 53 ? 63 ? 73 ? 83 ? 93 ?103 可表示为 n3 .
n?1
通过对以上材料的阅读,请解答下列问题.
2497449912485
(1) 2 ? 4 ? 6 ? 8 ?10 ? ?100 (即从 2 开始的 100 以内的连续偶数的和)用求和符合可表示为 .
(2)计算?(n2 ?1)? .(填写最后的计算结果).
n?1
【难度】★★★
?
50
【答案】(1) 2n ;(2)50.
n?1
34885768063【解析】(1)由题意可得, 2 ? 4 ? 6 ? 8 ? ?100 中,每一项的表示是 2n,总共是 50 项,所
?
50
以用求和符号表示为 2n ;
n?1
5
(2)当n ? 5 时,每项的和为??n2 ?1?? 0 ? 3 ? 8 ? 15 ? 24 ? 50 .
n?1
【总结】本题属于找规律的题目,主要考查学生的分析能力和理解能力.
同课章节目录
