沪教版七年级数学秋季班第10讲:期中复习(二)教师版
文档属性
| 名称 | 沪教版七年级数学秋季班第10讲:期中复习(二)教师版 |
|
|
| 格式 | docx | ||
| 文件大小 | 169.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-21 00:00:00 | ||
图片预览





文档简介
期中复习二
内容分析
本节课的内容涵盖了整式的加减,整式的乘除,因式分解.通过对知识的梳理,做到准确计算,能够灵活应用.
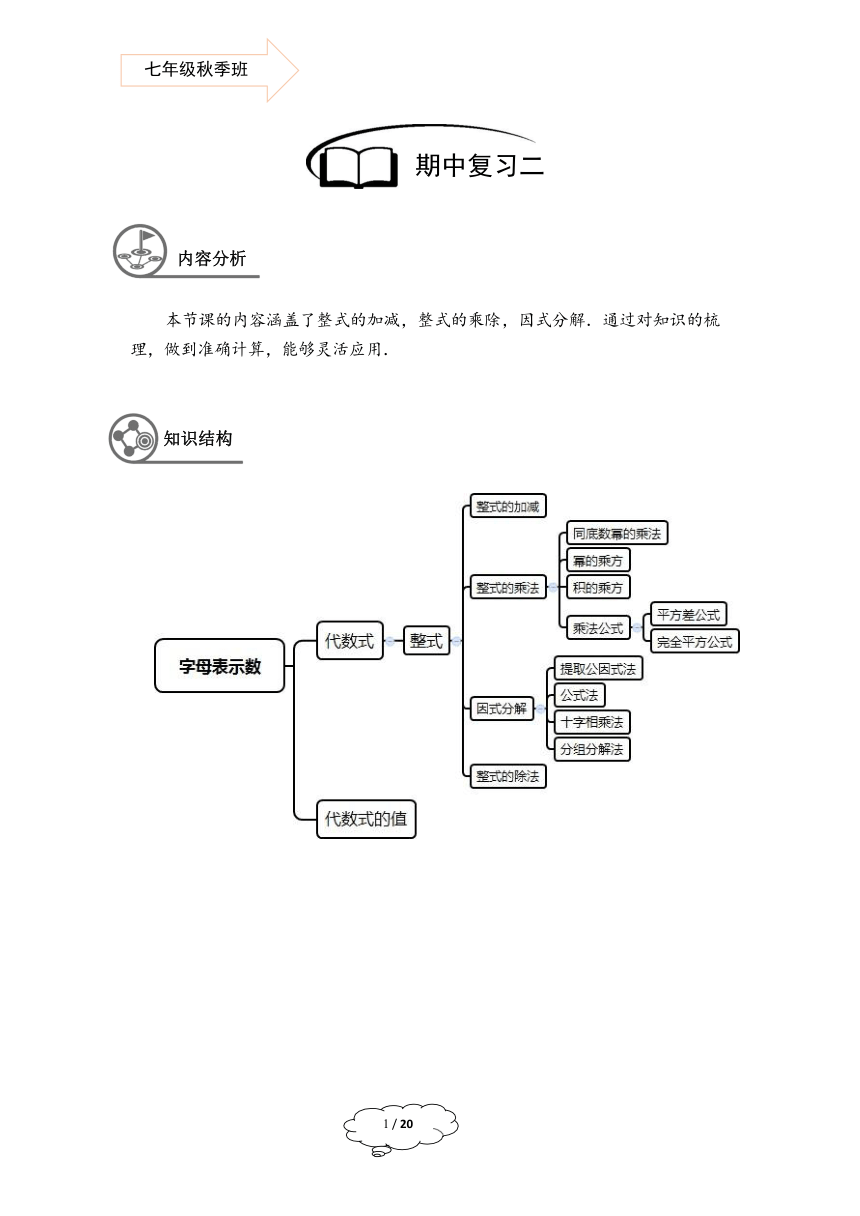
知识结构
1356870948300
选择题
【练习1】代数式?x3 ? 2x ? 24 是( ).
A .单项式 B .三次三项式 C .四次三项式 D .三次二项式
【难度】★
【答案】B
【解析】最高次数是 3,且含有三项,所以是三次三项式,故选 B.
【总结】本题主要考查多项式的相关概念,属于基础题.
【练习2】在代数式2a2 ? b , ? 1 , b , 2x2 ? x ? 5 , 0 中,下列结论正确的是( ).
2 2
A .有2 个多项式,1 个单项式 B .有2 个多项式, 2 个单项式
C .有2 个多项式, 3 个单项式 D .有5 个多项式
【难度】★
【答案】C
【解析】解:单项式中没有加减符号,单独的字母或数字也是单项式;多项式是由单项式相加减而成的,所以有三个单项式,二个多项式.
【总结】本题主要考查单项式和多项式的概念,属于基础题.
【练习3】下列各式中,运算正确的是( ).
A . x2 ? x2 ? x4 B . 3xm yn ? 2xm yn ? 1
C . 4x2 y3 ? 5x3 y2 ? 9x5 y5 D . ?5x2 y4 ? 3x2 y4 ? ?2x2 y4
【难度】★
【答案】D
【解析】合并同类项,字母及字母的次数不变,系数相加减.所以 A 相加的结果是2x2 ;B 相减的结果是 x m yn ;C 不是同类项,不能相加减.
【总结】本题主要考查合并同类项和同类项的概念.
【练习4】若关于 x 的积?x ? m??x ? 7? 中常数项为14 ,则 m 的值为( ).
A . 2 B . ?2
【难度】★
【答案】B
C . 7 D . ?7
【解析】解: ?x ? m??x ? 7? ? x2 ? ?7 ? m?x ? 7m ,所以?7m ? 14,m ? ?2 .
【总结】本题要清楚常数项的概念,先展开,再对应相等,要注意符号.
【练习5】下列各题中计算错误的是( ).
? 3 2
2 3 ?3
18 18
3 2 2 3 9 8
A . ????m ? ??n
? ??
? ?m n
B . ??m n? ??mn ? ? ?m n
? 2 2
3 ?3 6 6
2 3 2 3 9 9
C . ????m? ??n
【难度】★★
【答案】C
? ??
? ?m n
D . ??m n? ??mn ?
? m n
【解析】解:C 正确的计算是: ??-m?2 ??n2 ?3 ?3 ? ??m2 n6 ?3 ? ?m6n18 .
?? ?? ? ?
【总结】本题主要考查幂的乘方和同底数幂的乘法的混合运算.
【练习6】当 x ? 1 时,代数式 px3 ? qx ? 1 的值为2016 ,则当 x ? ?1 时,代数式 px3 ? qx ? 1 的
值为( ).
A . 2014 B . ?2015
【难度】★★
【答案】C
C . ?2014
D . ?2016
【解析】解:当 x ? 1 时,代入原式= p ? q ?1 ? 2016, p ? q ? 2015 ,当代入原式= ? p ? q ?1 ? ?2015 ?1 ? ?2014 .
【总结】本题主要考查代值求解,注意整体思想的运用.
x ? ?1 时,
【练习7】若?x ? a??x ? b? ? x2 ? kx ? ab ,则k 的值为( ).
A . a ? b
【难度】★★
【答案】B
B . ?a ? b
C . a ? b
D . b ? a
【解析】解: ?x ? a??x ? b? ? x2 ? ?a ? b?x ? ab ,所以?k ? a ? b ,k ? ?a ? b .
【总结】本题主要考查整式的乘法运算,注意符号的变化.
【练习8】若16 ? xn ? ?4 ? x2 ??x ? 2??2 ? x? ,则n 是( ).
A . 6 B . 4 C . 3 D . 2
【难度】★★
【答案】B
【解析】解:右边= ?4 ? x2 ??4 ? x2 ?? 16 ? x4 ,所以n ? 4 ..
【总结】本题主要考查了平方差公式的应用.
【练习9】设 M 是一个多项式,且 M ? 5 x2 y ? ?2x2 y4 ? 3 x ,那么 M 等于( ).
3 2
A . ? 6 x4 y5 ? 9 x4 y3
5 10
B . ? 6 y3 ? 5 xy
5 2
C . ?10 x4 y5 ? 5 x3 y
3 2
D . 10 x4 y5 ? 5 x3 y
3 2
【难度】★★
【答案】C
【解析】解: ? ?2x2 y4 ? 3
? 5 2
? ?10 x4 y5 ? 5 x3 y .
? 2 x ?. 3 x y 3 2
? ?
【总结】本题主要考查了单项式乘以多项式,注意法则的准确运用.
【练习10】不论 x、y 为何值,代数式 x2 ? y2 ? 2x ? 4 y ? 7 的值( ).
A .总不小于2 B .总不小于7
C .可为任何有理数 D .可能为负数
【难度】★★★
【答案】A
【解析】解: x2 ? 2x ?1 ? y2 ? 4 y ? 4 ? 2 ? ?x ? 1?2 ? ? y ? 2?2 ? 2
所以值总不会小于 2.
【总结】本题主要考查了完全平方公式的灵活运用,还有非负数相加求最值得问题.
【练习11】如果an2 ? ?an ?x ( n 为正整数),那么 x 等于( ).
A . n B . 2 C . an
【难度】★★★
【答案】A
【解析】解: an2 ? an?n ,而?an ?x ? an?x ,所以x ? n .
【总结】本题主要考查了幂的乘方.
填空题
【练习12】多项式5x3 ? 3x2 ? 2x ? 8 是 次 项式.
【难度】★
【答案】3;4.
【解析】解:未知数最高的次数是 3,总共 4 项,所以是 3 次 4 项式.
【总结】本题主要考查了多项式的相关知识点.
D . a2
【练习13】已知a、b 互为负倒数,c、d 互为相反数,且m 的绝对值为3 ,则
的值为 .
【难度】★
【答案】?10 .
ab ? m2 ? 3c ? 3d
班秋季级年七
5m
【解析】解:由题意可得, ab ? ?1,c ? d ? 0,m ? 3,m2 ? 9 , 代入原式? ?1? 9 ? ?10 .
【总结】本题主要考查代值求解,负倒数就是两数相乘为-1.
【练习14】若代数式2a2 ? 3a ? 7 的值为8 ,则代数式4a2 ? 6a ? 9 的值为 .
【难度】★
【答案】-7.
【解析】解: 2a2 ? 3a ? 7 ? 8 ,2a2 ? 3a ? 1,所以4a2 ? 6a ? 9 ? 2 ?2a2 ? 3a?? 9 ? 2 ? 9 ? ?7 .
【总结】本题主要考查代值求解,要学会整体代入思想的运用.
【练习15】已知多项式 x2 ? ax ?1与2x ? b 的乘积中含 x2 项的系数为3 ,含 x 项的系数是2 , 则 a ? b ???.
【难度】★
【答案】 3 或3 .
2
或
? ?
【解析】解:由题意可得, ?x2 ? ax ? 1?? ?2x ? b? ? 2x3 ? ?2a ? b? x2 ? ?2 ? ab? x ? b ,
?2a ? b ? 3
?a ? 0 ?a ? 3 3
?
所以?2 ? ab ? 2
,解得: ? ?
?b 3
2 ,所以a ? b ? 3或a ? b ? .
2
??b ? 0
【总结】某项的系数,要先相乘,然后合并同类项,再对应某项的系数,注意两种情况的讨论.
【练习16】若 x2 ? y2 ? 6 , x ? y ? 3 ,则 x ? y ???.
【难度】★
【答案】2
x2 ? y2
【解析】解:
? 6 ,?x ? y??x ? y? ? 6 ,又 x ? y ? 3,? x ? y ? 2 .
【总结】本题主要考查了平方差的应用.
【练习17】若3m ? 5 , 3n ? 4 ,则32m?n ???.
【难度】★
【答案】 25 .
4
【解析】解: 32m?n ? 32m ? 3n ,因为3m ? 5 ,3n ? 4 ,代入原式= 52 ? 4 ? 25 .
4
【总结】本题主要考查同底数幂的除法,注意整体代换的思想的应用.
【练习18】计算: ?18a2b ? 9a5b2 ?? ??3ab? ? .
【难度】★
【答案】?6a ? 3a4b .
【解析】解:原式=18a2b ? ??3ab? ? 9a5b2 ? ??3ab? ? ?6a ? 3a4b .
【总结】本题主要考查多项式除以单项式的计算,属于基础题.
【练习19】设 M ? 3a3 ?10a2 ? 5 , N ? ?2a3 ? 5 ?10a , P ? 7 ? 5a ? 2a2 ,那么 M ? 2N ? 3P
???, M ? 3N ? 2P ???.
【难度】★★
【答案】?a3 ? 4a2 ? 5a ?16 ; 9a3 ?14a2 ? 20a ? 6 .
【解析】由题意可得: M ? 3a3 ?10a2 ? 5 , 2N ? ?4a3 ?10 ? 20a , 3P ? 21?15a ? 6a2 , 所以 M ? 2N ? 3P ? ?a3 ? 4a2 ? 5a ?16 ;
同理, M ? 3a3 ?10a2 ? 5 , 2P ? 14 ?10a ? 4a2 , 3N ? ?6a3 ? 30a ?15 , 所以 M ? 3N ? 2P ? 9a3 ?14a2 ? 20a ? 6 .
【总结】本题主要考查了多项式的加减.去括号要注意括号前面是减号的时候,去掉括号后, 里面每项要变号.
【练习20】已知 xy ? 2(x ? y) ,那么 5x ? xy ? 5 y 的值为 .
3xy ? x ? y
【难度】★★
3
【答案】 .
5
【解析】解:因为 xy ? 2?x ? y ?,所以原式= 5x ? 2x ? 2 y ? 5 y ? 3x ? 3y ? 3 .
6x ? 6 y ? x ? y 5x ? 5 y 5
【总结】本题主要考查整体代换的思想的应用.
【练习21】已知?x2 ? px ? 8??x2 ? 3x ? q?的展开式中不含 x 项,且常数项为24 ,
则 p ???, q ???..
【难度】★★
【答案】8,3.
【解析】展开多项式,原式= x4 ? 3x3 ? qx2 ? px3 ? 3 px2 ? qpx ? 8x2 ? 24x ? 8q
? x4 ? ? p ? 3? x3 ? ?q ? 3p ? 8?x2 ? ?qp ? 24?x ? 8q .
?qp ? 24 ? 0
因为不含 x 项,且常数项为 0,所以?
?8q ? 24
? p ? 8
?
,解得:?q ? 3 .
【总结】本题主要考查多项式乘以多项式,不含某项,就是某项的系数为 0.
【练习22】已知32x?1 ? 1 ,则 x ???.
【难度】★
【答案】? 1 .
2
【解析】解:由题意得, 2x ?1 ? 0 ,x ? ? 1
2
【总结】本题主要考查某数(不为 0)的 0 次幂等于 1.
【练习23】若 a2n ? 3 ,则?a3n ?4 ? .
【难度】★★
【答案】729.
【解析】解:因为a2n ? 3,所以?a3n ?4 ? ?a2n ?6 ? 36 ? 729 .
【总结】本题主要考查了幂的乘方的灵活运用,还有整体代换的思想.
【练习24】若2x ? 5y ? 3 ? 0 ,则4x ? 32y 的值为 .
【难度】★★
【答案】8
【解析】解:因为2x ? 5y ? 3 ? 0
所以22 x 25 y ? 22 x?5 y ? 23 .
【总结】本题主要考查同底数幂的乘法的灵活运用,要学会观察指数之间的关系.
?
? 1 1 1 1 10 10
【练习25】计算: ? ? ? ? ? ? ? ? ?1? ? ?10 ? 9 ? 8 ? 7 ? ? ? ? ? 2 ?1? ?
? 10 9 8 2 ?
【难度】★★
【答案】1.
? 1 ?10
? 1 ?10
4430274220852? 1 ?10
【解析】解:原式= ? ? ?1010 ? ? ? ? 910 ? ? ?
? 810 ? ?110 ?110 ? 1 .
? 10 ? ? 9 ? ? 8 ?
【总结】本题主要考查积的乘方,要学会观察前面的式子和后面的式子的关系,然后灵活运用公式及逆用公式.
【练习26】若 m ? n ? 3 ,则2m2 ? 4mn ? 2n2 ? 6 的值为 .
【难度】★★
【答案】12
【解析】因为m ? n ? 3 ,所以原式? 2(m ? n)2 ? 6 ? 18 ? 6 ? 12 .
【总结】本题主要考查完全平方公式,要熟练运用公式.
【练习27】用边长为1cm 的小正方形搭如下的塔状图形, 则第 n 次所搭图形的周长是
cm .(用含n 的代数式表示)
【难度】★★★
【答案】4n .
【解析】解:第一次的周长是:4cm,第二次的
第 1 次 第 2 次 第 3 次 第 4 次
周长是 8cm,第三次的周长是 12cm,第四次的周长是 16cm,所以第 n 次所搭图形的周长是 4ncm.
【总结】本题属于找规律的题目,主要考查学生的分析能力和思维能力.
【练习28】若代数式 x2 ? y2 ?14x ? 2 y ? 50 的值为0 ,则 x ? y ???.
【难度】★★★
【答案】6
【解析】解:将原代数式分解为: x2 ?14x ? 49 ? y2 ? 2 y ? 1 ? 0 ,
? ? ? ?
2 2 ?x ? 7 ? 0 ?x ? 7
则 x ? 7 ? y ? 1 ? 0 , 所以 ,解得:
,? x ? y ? 7 ?1 ? 6 .
?
?
? y ? 1 ? 0 ? y ? ?1
【总结】本题包含了两个完全平方公式,不仅仅考查了学生的配平方公式,还考查了学生的观察能力和对完全平方公式的熟练程度.
【练习29】已知a ? b ? b ? c ? 3 , a2 ? b2 ? c2 ? 1 ,则ab ? bc ? ca 的值等于 .
5
【难度】★★★
【答案】? 2 .
25
【解析】解:由a ? b ? b ? c ? 3 ,可得: ?a ? b?2 ? a2 ? b2 ? 2ab ? 9 ,
5 25
?b ? c?2 ? b2 ? c2 ? 2bc ?
9 , ?a ? c?2 ? a2 ? c2 ? 2ac ? 36 ,
25 25
? ?
所以把三个式子相加可得: 2 a2 ? b2 ? c2 ? 2?ab ? bc ? ac? ? 54 ,
25
因为a2 ? b2 ? c2 ? 1 ,代入可得: ab ? bc ? ac ? ? 2 .
25
【总结】本题主要考查对完全平方公式的灵活运用.
解答题
【练习30】当 x ? 0.99 时,求3 ? ?3 ? ??2 ? ?2 ? x? ? x?? ? x?的值.
【难度】★
【答案】0.99
【解析】解:原式= 3 ? ?3 ? ?2 ? 2 ? x ? x?? x?? 3 ? ?3 ? x? ? 3 ? 3 ? x ? x ,
当 x ? 0.99 时,原式=0.99.
【总结】本题主要考查代数式求值,先化简,再求值.
4579111299295【练习31】有理数a、b、c 在数轴上对应点为 A、B、C .其位置如图所示,化简下式并合并同类项: c ? c ? b ? a ? c ? b ? a .
【难度】★
【答案】?c .
【解析】解:由图可得, c ? 0,c ? b ? 0,a ? c ? 0,b ? a ? 0 , 所以原式? ?c ? c ? b ? a ? c ? b ? a ? ?c .
【总结】本题主要考查合并同类项,并且同时考查了带绝对值的化简.
【练习32】已知多项式3xn?2 ? 2xn ? 4xn?3 ? 3xn?1 ( n 是大于3 的整数)是八次四项式,试确定下列各单项式的次数与系数:(1) ?n ? 3? xn y ;(2) ?n ? 3? xn?1 yn?2 .
【难度】★
【答案】(1)次数:6,系数:2; (2)次数:9,系数:8.
【解析】解:由题意可得, n ? 3 ? 8,则n ? 5 ,所以⑴中代入可得: ?n ? 3? xn y ? 2x5 y ,所以次数为 6,系数为 2;代入⑵中可得?n ? 3? xn?1 yn?2 ? 8x6 y3 ,所以次数为 9,系数为 8.
【总结】本题炸药考查了单项式和多项式的次数和系数相关知识点.
【练习33】如果单项式2mx a y 与?5nx2a ?3 y 是关于 x、y 的单项式,且它们是同类项.
(1)求?7a ? 22?2016 的值.(2)若2mxa y ? 5nx2a?3 y ? 0 ,且 xy ? 0 ,求?2m ? 5n?2003 的值.
【难度】★★
【答案】(1) 1; (2)0.
【解析】解:它们是同类项,可得a ? 2a ? 3 ,解得: a ? 3 , 代入(1)中得: ?7a ? 22?2016 ? ??1?2016 ? 1 ;
(2)因为2mxa y ? 5nx2a?3 y ? 0 ,且 xy ? 0 ,所以2m ? 5n , 代入可得?2m ? 5n?2003 ? 02003 ? 0 .
【总结】本题主要考查同类项的知识点,同时考查奇负偶正的问题.
【练习34】计算:
(1) ?3x2 ? 2x ? 1?? ?x2 ? x ? 3?; (2) ?a ? b ? 2c??a ? b ? 2c? ;
(3) ??a? 2 ???a3 ?? ??a? ? ??a2 ?3 ? ??a3 ?2 ; (4)??2x2 y ? 6x3 y4 ? 8xy ?? ??2xy ? ;
? 3 1 1
? ? 1 ?2
(5) ? a4b7 ? a3b8 ?
a2b6 ? ? ? ? ab3 ? .
? 4 2 9
? ? 3 ?
【难度】★★
【答案】(1) 2x2 ? x ? 2 ;(2) a2 ? b2 ? 2ab ? 4c2 ;(3) ?a6 ;(4) x ? 3x2 y3 ? 4 ;
(5) 27 a2b ? 9 ab2 ?1. 4 2
【解析】(1)原式? 3x2 ? 2x ?1? x2 ? x ? 3 ? 2x2 ? x ? 2 ;
(2)原式? ?a ? b?2 ? 4c2 ? a2 ? b2 ? 2ab ? 4c2 ;
(3)原式? a6 ? a6 ? a6 ? ?a6 ;
(4)原式= (?2x2 y) ? (?2xy) ? 6x3 y4 ? (?2xy) ? (?8xy) ? (?2xy)
= x ? 3x2 y3 ? 4 ;
(5)原式? 3 a4b7 ? 1 a2b6 ? 1 a3b8 ? 1 a2b6 ? 1 a2b6 ? 1 a3b6
4 9 2 9 9 2
? 27 a2b ? 9 ab2 ?1 .
4 2
【总结】本题主要考查了整式的基本运算,注意相关法则的准确运用.
【练习35】先化简,再求值: ??2x2 ? (x ? y)(x ? y)?? ??(?x ? y)(?x ? y) ? 2 y2 ?? ,其中 x ? 1 ,
y ? ?2 .
【难度】★★
【答案】25
【解析】原式 ? ??2x2 ? x2 ? y2 ?? ??x2 ? y2 ? 2 y2 ??
? ?x2 ? y2 ??x2 ? y2 ? ? ?x2 ? y2 ?2 .
141076644913x ? 1,y ? ?2 ,?原式 ? (1 ? 4)2 ? 25 .
【总结】本题主要考查多项式的化简求值.
【练习36】解不等式: 2x ? (5 ? x)(x ?1) ? x(x ?1) ? 4 .
【难度】★★
【答案】 x ? ?9 .
【解析】解: 2x ? ?5x ? 5 ? x2 ? x?? x2 ? x ? 4
2x ? 4x ? x 2 ?5 ? x2 ? x ? 4
-x ? 9
x ? ?9
【总结】本题主要考查多项式的计算与不等式的结合.
【练习37】解方程: (x ? 3)(x ? 3) ? (2x ?1)(x ? 7) ? x2 .
【难度】★★
【答案】 x ?? 2 .
13
【解析】解: x2 ? 9 ? 2x2 ?14x ? x ? 7 ? x2
x2 ? 9 ? 2x2 ?13x ? 7x2
13x ? ?2
x ?? 2
13
【总结】本题结合了多项式和方程,同时考查学生的应变能力.
【练习38】计算: ?1 ? 1 ??1 ? 1 ??1 ? 1 ? ? ? ? ?1 ?
??
1 ? .
? 22 ?? 32 ?? 42 ? ?
202 ?
【难度】★★
【答案】 21 .
40
? ?? ?? ? ? ?
【解析】解: 原式 ? ?1 ? 1 ??1 ? 1 ??1 ? 1 ??1 ? 1 ???1 ?
???
1 ??1 ? 1 ?
?
? 2 ??
2 ??
3 ??
3 ? ?
20 ??
20 ?
? ?? ?? ?? ? ? ?? ?
? 1 ? 5 21
2 4 20
? 1 ? 21
2 20
? 21
40
【总结】本题主要考查平方差公式的灵活运用.
【练习39】试证明:
(1) 22005 ? 22004 ? 22003 能被5 整除;
(2)若n 是正整数,试说明3n?3 ? 4n?1 ? 3n?1 ? 22n 能被10 整除.
【难度】★★
【答案】略.
【解析】(1) 原式? 2222003 ? 2 ? 22003 ? 22003 ? 6 ? 22003 ? 22003 = 5 ? 22003 ,
所以能被 5 整除;
(2) 原式 ? ?3n?3 ? 3n?1 ?? ?4n?1 ? 22n ? ? ?32 ? 3n ?1 ? 3n ?1 ?? ?4n ?1 ? 4n ?
? 10 ? 3n?1 ? 5 ? 4n
所以能被 10 整除.
? 10 ? 3n?1 ?10 ? 22n?1 ,
【总结】能被某数整除的数可以分解成该数乘以另外一个数或式子.
【练习40】计算:
(1)已知9m ? 27m?1 ? 32m ? 27 ,求m 的值.
? 8 ?
4
(2)已知?16x2 ?3 ? ? 1 ?
? ?
? 5 ,求 x12 的值.
(3)已知2n ? a , 3n ? b ,求4n ? 6n ? 9n 的值.
(4)已知2a ? 3 , 2b ? 6 , 2c ? 12 ,求a、b、c 之间的一个数量关系式.
(5)比较大小: 244 , 333 , 422 .
【难度】★★
【答案】(1) m ? 2 ;(2) 25 ;(3) a2 ? ab ? b2 ;(4) 2b ? a ? c ;(5) 333 ? 422 ? 244 .
【解析】解:(1)因为9m ? 27m?1 ? 32m ? 27 ,所以32m ? 33m?3 ? 32m ? 33 ,即33m?3 ? 33 , 所以3m ? 3 ? 3 ,所以m ? 2 ;
1544751105041 4 12
(2) ?16x2 ?3 .? 1 ? ? 5 ,?24 x2 ?3 .? 1 ?
?
? 5 ,
8 2
? ? ? ?
? ? ? ?
? x6 ? 5,? x12 ? ?x6 ?2 ? 52 ? 25 .
1544751104661(3) 2n ? a ,3n ? b ,?4n ? 6n ? 9n ? ?22 ?n ? ?2 ? 3?n ? ?32 ?n ? a2 ? ab ? b2 ;
154475048088(4) 2a ? 3,2b ? 6 ,2c ? 12 ,?2a ? 2c ? 2a?c ? 3?12 ? 36 ,2b ? 2b ? 22b ? 6 ? 6 ? 36 ,
所以2b ? a ? c .
(5)观察发现, 244 ? ?24 ?11 ? 1611 ,333 ? ?33 ?11 ? 2711 ,422 ? ?42 ?11 ? 1611 ,因为1611 ? 2711 ,所以333 ? 244 ? 422 .
【总结】本题主要考查了幂的运算,以及比较大小.比较大小时,要么化成底数相同,比较
指数大小,要么化成指数相同,比较底数大小.
【练习41】如果?x ? a??x ? 4? ?1能够分解成两个多项式 x ? b 、x ? c 的乘积( b、c 为整数),求 a 的值.
【难度】★★
【答案】a ? 4 .
【解析】解:因为?x ? a??x ? 4??1 ? x2 ? ?a ? 4?x ? 4a ? 1,
又 ?x ? b??x ? c? ? x2
??? ?4 ? a? ? b ? c
? ? ? ? ? ,所以
b c x bc ?
??4a ?1 ? bc
,则?4b ? 4c ?17 ? bc ,
整理可得: ?b ? 4??c ? 4? ? ?1
,因为 b、c 为整数,所以 b、c 一个取-3,一个取-5,
代入得a ? 4 .
【总结】本题要注意后面的解题思路,利用 b、c 为整数这个条件,可以得出最后的结果.
【练习42】已知?a ? b?2 ? 12 , ?a ? b?2 ? 3 ,求:(1) ab ;(2) a2 ? b2 ;(3) a2 ? b2 的值.
【难度】★★
【答案】(1) 9 ;(2) 15 ;(3) ?6 .
4 2
【解析】解:由题意可得, ?a ? b?2 ? a2 ? 2ab ? b2 ? 12 ,?a ? b?2 ? a2 ? 2ab ? b2 ? 3 ,
所以(1)中求ab ,两式相减可得: 4ab ? 9 ,ab ? 9 ;
4
2
(2)两式相加可得: 2?a2 ? b2 ?? 15,则a2 ? b2 ? 15 ;
(3)因为a2 ? b2 ? ?a ? b??a ? b?,所以?a ? b?2 ? ?a ? b?2 ? 12 ? 3 ? 36 ,所以?a ? b?? ?a ? b? ? ?6 .
【总结】本题主要考查平方差公式和完全平方公式的综合运用.
【练习43】已知多项式 A 除以4x3 ? 3x2 ?1 得商式3x2 ? 3x ,余式 x2 ?1 ,求多项式 A .
【难度】★★
【答案】 A ? 12x5 ? 21x4 ? 9x3 ? 2x2 ? 3x ?1.
【解析】解:由题意可知,商×除式+余式=被除式,
所以 A ? (3x2 ? 3x) ? (4x3 ? 3x2 ?1) ? x2 ?1 ? 12x5 ? 21x4 ? 9x3 ? 2x2 ? 3x ?1 .
【总结】该题实际还是考查多项式×多项式的计算,同时有方程的思想在里面.
1 1 ? 1 ?2 1
【练习44】已知 x ? ? 3 ,求:(1) x2 ? ;(2) ? x ? ? ;(3) x4 ? 的值.
x x2 ? x ? x4
【难度】★★
【答案】(1)7;(2)5;(3)47.
1 ?
1 ?2 1 1
【解析】解:(1)因为 x ? ? 3,所以? x ? ? ? x2 ? ? 2 ? 9 ,所以x2 ? ? 7 ;
x ? x ? x2 x2
? 1 ?2 ? 1 ?2
? 1 ?2
(2)因为? x ? x ? ? ? x ? x ? ? 4 ,所以? x ? x ?
? 9 ? 4 ? 5 ,
? ? ? ? ? ?
1 ? 1 ?2 1 1
(3)由(1)知 x2 ? ? 7 ,所以? x2 ? ? ? x4 ? ? 2 ? 49 ,所以x4 ? ? 47 .
x2 ? x2 ? x4 x4
【总结】本题主要考查两个互为倒数的数的平方的规律,中间项为常数项.
【练习45】分解因式:
(1) ?x ? 2??x ? 4? ? x2 ?16 ; (2) 4m2 ?x ? y?3 ? ? y ? x?3 ?m ? n?2
(3)16a4 ? 72a2 ? 81; (4)?x ? 5y?2 ? (2x ?10 y)(3x ? y) ? ?3x ? y ?2 ;
(5) ?x2 ? x?2 ?18?x2 ? x?? 72 ; (6) a4 ? a2 ? 4a ? 4 ;
(7) ?x2 ? x ? 1??x2 ? x ? 2??12 .
【难度】★★
【答案】(1) 2?x ? 4??x ?1? ;(2) ?x ? y?3 ?3m ? n??m ? n? ;(3) (2a ? 3)2 (2a ? 3)2 ;
(4)16?x ? y ?2 ;(5) ?x ? 3??x ? 2??x ? 4??x ? 3? ;(6) ?a ? 2??a ?1??a2 ? a ? 2? ;
(7) ?x2 ? x ? 5??x ? 2??x ?1?.
【解析】解:(1)原式= ?x ? 2??x ? 4? ? ?x ? 4??x ? 4? ? ?x ? 4??x ? 2 ? x ? 4? ? 2 ?x ? 4??x ? 1? ;
? ?
(2)原式= ?x ? y ?3 ?4m2 ? ?m ? n?2 ? ? ?x ? y ?3 ?2m ? m ? n??2m ? m ? n?
? ?x ? y?3 ?3m ? n??m ? n? ;
(3)原式= ?4a2 ? 9?2 ? (2a ? 3)2 (2a ? 3)2 ;
(4)原式= ?x ? 5y?2 ? 2(x ? 5y)(3x ? y) ? ?3x ? y?2 ? ?x ? 5y ? 3x ? y?2
? ?4x ? 4 y?2 ? 16?x ? y?2 ;
(5)原式= ?x2 ? x ? 6??x2 ? x ? 12?? ?x ? 3??x ? 2??x ? 3??x ? 4? ;
(6)原式= a4 ? ?a2 ? 4a ? 4?? a4 ? ?a ? 2?2
? ?a2 ? a ? 2??a2 ? a ? 2?? ?a ? 2??a ?1??a2 ? a ? 2?;
(7)原式? ?x2 ? x?2 ? 3(x2 ? x) ?10 ? (x2 ? x ? 5)(x2 ? x ? 2)
? (x2 ? x ? 5)(x ? 2)(x ?1) .
【总结】本题主要考查因式分解,一定要分解到不能再分解为止.
【练习46】已知多项式 x2 ? xy ? 12 y2 ,(1)将此多项式因式分解;(2)若多项式 x2 ? xy ? 12 y2
的值等于?6 ,且 x、y 都是整数,求满足条件的 x、y 的值.
【难度】★★
? ? ?
【答案】(1) ?x ? 4 y ??x ? 3y ? ;⑵ ?x ? 3, ?x ? 2
, ?x ? ?3, ?x ? ?2
?
? y ?
1 ? y ? ?1 ? y ? ?1 ? y ? 1
【解析】解:(1)将原式因式分解= ?x ? 4 y ??x ? 3y ? ;
174477676692(2) x2 ? xy ?12y2 ? ?x ? 4y??x ? 3y?,??x ? 4y??x ? 3y? ? ?6 ,
则有?6 ? ??1?? 6 ? ??6??1 ? ??2?? 3 ? ??3?? 2 ,又 x ? 3y ? ?x ? 4y
?? 7y
,所以两个数相
减一定是 7 的倍数,则只能去-1 和 6,或者-6 和 1 这两组,所以有
?x ? 4 y ? ?1
?x ? 4 y ? 6
?x ? 4 y ? 1
?x ? 4 y ? ?6
① ?x ? 3y ? 6 ,② ?x ? 3y ? ?1,③ ?x ? 3y ? ?6 ,④ ?x ? 3y ? 1 ,
? ? ? ?
分别解可得: ?x ? 3
?x ? 2
?x ? ?3
?x ? ?2 .
? ? ? ?
? y ? 1 ,? y ? ?1,? y ? ?1,? y ? 1
【总结】本题不仅仅考查因式分解,还考查了分类讨论的思想.
【练习47】已知2x2 ? 3x ? 4 ? a ?x ?1?2 ? b ?x ?1? ? c ,求a 、b 、c 的值.
【难度】★★
【答案】a ? 2,b ? 7 ,c ? 9 .
【解析】右边的多项式展开= ax2 ? ?b ? 2a? x ? ?a ? b ? c?,对应未知数的系数相等可得,
?a ? 2 ?a ? 2
? ?
?b ? 2a ? 3
?a ? b ? c ? 4
,所以解得:?b ? 7 .
?c ? 9
? ?
【总结】本题中两个多项式相等,则对应的系数也相等.
【练习48】已知 x ? y ,且 x2 ? x ? 2 , y2 ? y ? 2 ,求代数式 x2 ? xy ? y2 .
【难度】★★★
【答案】7.
194416685597【解析】解:
x2 ? x ? 2 ,x2 ? x ? 2 ? 0 ,??x ? 2??x ?1? ? 0 ,解得: x ? 2或x ? ?1 ,
同理可解得: y ? 2或y ? ?1 ,因为 x ? y ,所以一个取 2,一个取-1,代入可得:
x2 ? xy ? y2 ? 22 ? 2 ? 12 ? 7 .
【总结】本题要利用因式分解解出 x、y 的取值,再代入.
【练习49】计算: ?2 ? 1??22 ? 1??24 ? 1??28 ? 1?? ? ? ?232 ? 1?.
【难度】★★★
【答案】264 ?1 .
425250995953【解析】解:原式? ?2 ?1??2 ? 1??22 ? 1??24 ? 1??28 ? 1? ?232 ? 1?
3692222176247? ?22 ?1??22 ? 1??24 ? 1??28 ? 1? ?232 ? 1?
3279632177517? ?24 ?1??24 ? 1??28 ? 1? ?232 ?1?
? 264 ? 1 .
【总结】本题很灵活的运用平方差公式解题,同时考查学生的观察能力.
【练习50】若 A ? ?3 ? 1??32 ? 1??34 ? 1??38 ? 1??316 ? 1??332 ? 1??364 ? 1? ,求 A ? 2002 的末位数字.
【难度】★★★
【答案】末尾数是 5
2
【解析】解:A ? 1 (3 ?1) ?3 ?1??32 ?1??34 ?1??38 ?1??316 ?1??332 ?1??364 ?1?
2
? 1 (32 ?1)?32 ?1??34 ?1??38 ?1??316 ?1??332 ?1??364 ?1?
? 1 (3128 ?1) ,
2
400707145158因为31 ? 3,32 ? 9 ,33 ? 27 ,34 ? 81,35 ? 243
,由此可见,每四个末尾数就开始重复
3、9、7、1,128 ? 4 ? 32 ,所以3128 的末尾数是 1,减去 1 后,末尾数是 0,再×0.5 , 末尾数就是 5.
【总结】本题主要考查的是学生的分析能力和观察能力,是否能找到隐藏的规律.
【练习51】已知a2 ? 2a ? b2 ? 6b ?10 ? 0 ,求a2 ? b2 的值.
【难度】★★★
【答案】10.
【解析】解:由题意可得: a2 ? 2a ?1 ? b2 ? 6b ? 9 ? ?a ? 1?2 ? ?b ? 3?2 ? 0 ,
? ?
所以有?a ? 1 ? 0 ,? ?a ? ?1 ,代入后有a2 ? b2 ? 1? 9 ? 10 .
?b ? 3 ? 0 ?b ? 3
【总结】本题主要考查了配方法的运用,还是非负数之和为 0 的情况.
【练习52】证明:四个连续整数的乘积加1是整数的平方.
【难度】★★★
【答案】略.
【解析】证明:设四个连续整数为n, n ? 1, n ? 2, n ? 3 ,则有
n ?n ? 1??n ? 2??n ? 3? ? 1
? ?n2 ? 3n??n2 ? 3n ? 2?? 1
? ?n2 ? 3n?2 ? 2?n2 ? 3n?? 1
? ?n2 ? 3n ? 1?2
【总结】本题要注意两两组合,把相同的部分n2 ? 3n 看成一个整体,再进行完全平方.
内容分析
本节课的内容涵盖了整式的加减,整式的乘除,因式分解.通过对知识的梳理,做到准确计算,能够灵活应用.
知识结构
1356870948300
选择题
【练习1】代数式?x3 ? 2x ? 24 是( ).
A .单项式 B .三次三项式 C .四次三项式 D .三次二项式
【难度】★
【答案】B
【解析】最高次数是 3,且含有三项,所以是三次三项式,故选 B.
【总结】本题主要考查多项式的相关概念,属于基础题.
【练习2】在代数式2a2 ? b , ? 1 , b , 2x2 ? x ? 5 , 0 中,下列结论正确的是( ).
2 2
A .有2 个多项式,1 个单项式 B .有2 个多项式, 2 个单项式
C .有2 个多项式, 3 个单项式 D .有5 个多项式
【难度】★
【答案】C
【解析】解:单项式中没有加减符号,单独的字母或数字也是单项式;多项式是由单项式相加减而成的,所以有三个单项式,二个多项式.
【总结】本题主要考查单项式和多项式的概念,属于基础题.
【练习3】下列各式中,运算正确的是( ).
A . x2 ? x2 ? x4 B . 3xm yn ? 2xm yn ? 1
C . 4x2 y3 ? 5x3 y2 ? 9x5 y5 D . ?5x2 y4 ? 3x2 y4 ? ?2x2 y4
【难度】★
【答案】D
【解析】合并同类项,字母及字母的次数不变,系数相加减.所以 A 相加的结果是2x2 ;B 相减的结果是 x m yn ;C 不是同类项,不能相加减.
【总结】本题主要考查合并同类项和同类项的概念.
【练习4】若关于 x 的积?x ? m??x ? 7? 中常数项为14 ,则 m 的值为( ).
A . 2 B . ?2
【难度】★
【答案】B
C . 7 D . ?7
【解析】解: ?x ? m??x ? 7? ? x2 ? ?7 ? m?x ? 7m ,所以?7m ? 14,m ? ?2 .
【总结】本题要清楚常数项的概念,先展开,再对应相等,要注意符号.
【练习5】下列各题中计算错误的是( ).
? 3 2
2 3 ?3
18 18
3 2 2 3 9 8
A . ????m ? ??n
? ??
? ?m n
B . ??m n? ??mn ? ? ?m n
? 2 2
3 ?3 6 6
2 3 2 3 9 9
C . ????m? ??n
【难度】★★
【答案】C
? ??
? ?m n
D . ??m n? ??mn ?
? m n
【解析】解:C 正确的计算是: ??-m?2 ??n2 ?3 ?3 ? ??m2 n6 ?3 ? ?m6n18 .
?? ?? ? ?
【总结】本题主要考查幂的乘方和同底数幂的乘法的混合运算.
【练习6】当 x ? 1 时,代数式 px3 ? qx ? 1 的值为2016 ,则当 x ? ?1 时,代数式 px3 ? qx ? 1 的
值为( ).
A . 2014 B . ?2015
【难度】★★
【答案】C
C . ?2014
D . ?2016
【解析】解:当 x ? 1 时,代入原式= p ? q ?1 ? 2016, p ? q ? 2015 ,当代入原式= ? p ? q ?1 ? ?2015 ?1 ? ?2014 .
【总结】本题主要考查代值求解,注意整体思想的运用.
x ? ?1 时,
【练习7】若?x ? a??x ? b? ? x2 ? kx ? ab ,则k 的值为( ).
A . a ? b
【难度】★★
【答案】B
B . ?a ? b
C . a ? b
D . b ? a
【解析】解: ?x ? a??x ? b? ? x2 ? ?a ? b?x ? ab ,所以?k ? a ? b ,k ? ?a ? b .
【总结】本题主要考查整式的乘法运算,注意符号的变化.
【练习8】若16 ? xn ? ?4 ? x2 ??x ? 2??2 ? x? ,则n 是( ).
A . 6 B . 4 C . 3 D . 2
【难度】★★
【答案】B
【解析】解:右边= ?4 ? x2 ??4 ? x2 ?? 16 ? x4 ,所以n ? 4 ..
【总结】本题主要考查了平方差公式的应用.
【练习9】设 M 是一个多项式,且 M ? 5 x2 y ? ?2x2 y4 ? 3 x ,那么 M 等于( ).
3 2
A . ? 6 x4 y5 ? 9 x4 y3
5 10
B . ? 6 y3 ? 5 xy
5 2
C . ?10 x4 y5 ? 5 x3 y
3 2
D . 10 x4 y5 ? 5 x3 y
3 2
【难度】★★
【答案】C
【解析】解: ? ?2x2 y4 ? 3
? 5 2
? ?10 x4 y5 ? 5 x3 y .
? 2 x ?. 3 x y 3 2
? ?
【总结】本题主要考查了单项式乘以多项式,注意法则的准确运用.
【练习10】不论 x、y 为何值,代数式 x2 ? y2 ? 2x ? 4 y ? 7 的值( ).
A .总不小于2 B .总不小于7
C .可为任何有理数 D .可能为负数
【难度】★★★
【答案】A
【解析】解: x2 ? 2x ?1 ? y2 ? 4 y ? 4 ? 2 ? ?x ? 1?2 ? ? y ? 2?2 ? 2
所以值总不会小于 2.
【总结】本题主要考查了完全平方公式的灵活运用,还有非负数相加求最值得问题.
【练习11】如果an2 ? ?an ?x ( n 为正整数),那么 x 等于( ).
A . n B . 2 C . an
【难度】★★★
【答案】A
【解析】解: an2 ? an?n ,而?an ?x ? an?x ,所以x ? n .
【总结】本题主要考查了幂的乘方.
填空题
【练习12】多项式5x3 ? 3x2 ? 2x ? 8 是 次 项式.
【难度】★
【答案】3;4.
【解析】解:未知数最高的次数是 3,总共 4 项,所以是 3 次 4 项式.
【总结】本题主要考查了多项式的相关知识点.
D . a2
【练习13】已知a、b 互为负倒数,c、d 互为相反数,且m 的绝对值为3 ,则
的值为 .
【难度】★
【答案】?10 .
ab ? m2 ? 3c ? 3d
班秋季级年七
5m
【解析】解:由题意可得, ab ? ?1,c ? d ? 0,m ? 3,m2 ? 9 , 代入原式? ?1? 9 ? ?10 .
【总结】本题主要考查代值求解,负倒数就是两数相乘为-1.
【练习14】若代数式2a2 ? 3a ? 7 的值为8 ,则代数式4a2 ? 6a ? 9 的值为 .
【难度】★
【答案】-7.
【解析】解: 2a2 ? 3a ? 7 ? 8 ,2a2 ? 3a ? 1,所以4a2 ? 6a ? 9 ? 2 ?2a2 ? 3a?? 9 ? 2 ? 9 ? ?7 .
【总结】本题主要考查代值求解,要学会整体代入思想的运用.
【练习15】已知多项式 x2 ? ax ?1与2x ? b 的乘积中含 x2 项的系数为3 ,含 x 项的系数是2 , 则 a ? b ???.
【难度】★
【答案】 3 或3 .
2
或
? ?
【解析】解:由题意可得, ?x2 ? ax ? 1?? ?2x ? b? ? 2x3 ? ?2a ? b? x2 ? ?2 ? ab? x ? b ,
?2a ? b ? 3
?a ? 0 ?a ? 3 3
?
所以?2 ? ab ? 2
,解得: ? ?
?b 3
2 ,所以a ? b ? 3或a ? b ? .
2
??b ? 0
【总结】某项的系数,要先相乘,然后合并同类项,再对应某项的系数,注意两种情况的讨论.
【练习16】若 x2 ? y2 ? 6 , x ? y ? 3 ,则 x ? y ???.
【难度】★
【答案】2
x2 ? y2
【解析】解:
? 6 ,?x ? y??x ? y? ? 6 ,又 x ? y ? 3,? x ? y ? 2 .
【总结】本题主要考查了平方差的应用.
【练习17】若3m ? 5 , 3n ? 4 ,则32m?n ???.
【难度】★
【答案】 25 .
4
【解析】解: 32m?n ? 32m ? 3n ,因为3m ? 5 ,3n ? 4 ,代入原式= 52 ? 4 ? 25 .
4
【总结】本题主要考查同底数幂的除法,注意整体代换的思想的应用.
【练习18】计算: ?18a2b ? 9a5b2 ?? ??3ab? ? .
【难度】★
【答案】?6a ? 3a4b .
【解析】解:原式=18a2b ? ??3ab? ? 9a5b2 ? ??3ab? ? ?6a ? 3a4b .
【总结】本题主要考查多项式除以单项式的计算,属于基础题.
【练习19】设 M ? 3a3 ?10a2 ? 5 , N ? ?2a3 ? 5 ?10a , P ? 7 ? 5a ? 2a2 ,那么 M ? 2N ? 3P
???, M ? 3N ? 2P ???.
【难度】★★
【答案】?a3 ? 4a2 ? 5a ?16 ; 9a3 ?14a2 ? 20a ? 6 .
【解析】由题意可得: M ? 3a3 ?10a2 ? 5 , 2N ? ?4a3 ?10 ? 20a , 3P ? 21?15a ? 6a2 , 所以 M ? 2N ? 3P ? ?a3 ? 4a2 ? 5a ?16 ;
同理, M ? 3a3 ?10a2 ? 5 , 2P ? 14 ?10a ? 4a2 , 3N ? ?6a3 ? 30a ?15 , 所以 M ? 3N ? 2P ? 9a3 ?14a2 ? 20a ? 6 .
【总结】本题主要考查了多项式的加减.去括号要注意括号前面是减号的时候,去掉括号后, 里面每项要变号.
【练习20】已知 xy ? 2(x ? y) ,那么 5x ? xy ? 5 y 的值为 .
3xy ? x ? y
【难度】★★
3
【答案】 .
5
【解析】解:因为 xy ? 2?x ? y ?,所以原式= 5x ? 2x ? 2 y ? 5 y ? 3x ? 3y ? 3 .
6x ? 6 y ? x ? y 5x ? 5 y 5
【总结】本题主要考查整体代换的思想的应用.
【练习21】已知?x2 ? px ? 8??x2 ? 3x ? q?的展开式中不含 x 项,且常数项为24 ,
则 p ???, q ???..
【难度】★★
【答案】8,3.
【解析】展开多项式,原式= x4 ? 3x3 ? qx2 ? px3 ? 3 px2 ? qpx ? 8x2 ? 24x ? 8q
? x4 ? ? p ? 3? x3 ? ?q ? 3p ? 8?x2 ? ?qp ? 24?x ? 8q .
?qp ? 24 ? 0
因为不含 x 项,且常数项为 0,所以?
?8q ? 24
? p ? 8
?
,解得:?q ? 3 .
【总结】本题主要考查多项式乘以多项式,不含某项,就是某项的系数为 0.
【练习22】已知32x?1 ? 1 ,则 x ???.
【难度】★
【答案】? 1 .
2
【解析】解:由题意得, 2x ?1 ? 0 ,x ? ? 1
2
【总结】本题主要考查某数(不为 0)的 0 次幂等于 1.
【练习23】若 a2n ? 3 ,则?a3n ?4 ? .
【难度】★★
【答案】729.
【解析】解:因为a2n ? 3,所以?a3n ?4 ? ?a2n ?6 ? 36 ? 729 .
【总结】本题主要考查了幂的乘方的灵活运用,还有整体代换的思想.
【练习24】若2x ? 5y ? 3 ? 0 ,则4x ? 32y 的值为 .
【难度】★★
【答案】8
【解析】解:因为2x ? 5y ? 3 ? 0
所以22 x 25 y ? 22 x?5 y ? 23 .
【总结】本题主要考查同底数幂的乘法的灵活运用,要学会观察指数之间的关系.
?
? 1 1 1 1 10 10
【练习25】计算: ? ? ? ? ? ? ? ? ?1? ? ?10 ? 9 ? 8 ? 7 ? ? ? ? ? 2 ?1? ?
? 10 9 8 2 ?
【难度】★★
【答案】1.
? 1 ?10
? 1 ?10
4430274220852? 1 ?10
【解析】解:原式= ? ? ?1010 ? ? ? ? 910 ? ? ?
? 810 ? ?110 ?110 ? 1 .
? 10 ? ? 9 ? ? 8 ?
【总结】本题主要考查积的乘方,要学会观察前面的式子和后面的式子的关系,然后灵活运用公式及逆用公式.
【练习26】若 m ? n ? 3 ,则2m2 ? 4mn ? 2n2 ? 6 的值为 .
【难度】★★
【答案】12
【解析】因为m ? n ? 3 ,所以原式? 2(m ? n)2 ? 6 ? 18 ? 6 ? 12 .
【总结】本题主要考查完全平方公式,要熟练运用公式.
【练习27】用边长为1cm 的小正方形搭如下的塔状图形, 则第 n 次所搭图形的周长是
cm .(用含n 的代数式表示)
【难度】★★★
【答案】4n .
【解析】解:第一次的周长是:4cm,第二次的
第 1 次 第 2 次 第 3 次 第 4 次
周长是 8cm,第三次的周长是 12cm,第四次的周长是 16cm,所以第 n 次所搭图形的周长是 4ncm.
【总结】本题属于找规律的题目,主要考查学生的分析能力和思维能力.
【练习28】若代数式 x2 ? y2 ?14x ? 2 y ? 50 的值为0 ,则 x ? y ???.
【难度】★★★
【答案】6
【解析】解:将原代数式分解为: x2 ?14x ? 49 ? y2 ? 2 y ? 1 ? 0 ,
? ? ? ?
2 2 ?x ? 7 ? 0 ?x ? 7
则 x ? 7 ? y ? 1 ? 0 , 所以 ,解得:
,? x ? y ? 7 ?1 ? 6 .
?
?
? y ? 1 ? 0 ? y ? ?1
【总结】本题包含了两个完全平方公式,不仅仅考查了学生的配平方公式,还考查了学生的观察能力和对完全平方公式的熟练程度.
【练习29】已知a ? b ? b ? c ? 3 , a2 ? b2 ? c2 ? 1 ,则ab ? bc ? ca 的值等于 .
5
【难度】★★★
【答案】? 2 .
25
【解析】解:由a ? b ? b ? c ? 3 ,可得: ?a ? b?2 ? a2 ? b2 ? 2ab ? 9 ,
5 25
?b ? c?2 ? b2 ? c2 ? 2bc ?
9 , ?a ? c?2 ? a2 ? c2 ? 2ac ? 36 ,
25 25
? ?
所以把三个式子相加可得: 2 a2 ? b2 ? c2 ? 2?ab ? bc ? ac? ? 54 ,
25
因为a2 ? b2 ? c2 ? 1 ,代入可得: ab ? bc ? ac ? ? 2 .
25
【总结】本题主要考查对完全平方公式的灵活运用.
解答题
【练习30】当 x ? 0.99 时,求3 ? ?3 ? ??2 ? ?2 ? x? ? x?? ? x?的值.
【难度】★
【答案】0.99
【解析】解:原式= 3 ? ?3 ? ?2 ? 2 ? x ? x?? x?? 3 ? ?3 ? x? ? 3 ? 3 ? x ? x ,
当 x ? 0.99 时,原式=0.99.
【总结】本题主要考查代数式求值,先化简,再求值.
4579111299295【练习31】有理数a、b、c 在数轴上对应点为 A、B、C .其位置如图所示,化简下式并合并同类项: c ? c ? b ? a ? c ? b ? a .
【难度】★
【答案】?c .
【解析】解:由图可得, c ? 0,c ? b ? 0,a ? c ? 0,b ? a ? 0 , 所以原式? ?c ? c ? b ? a ? c ? b ? a ? ?c .
【总结】本题主要考查合并同类项,并且同时考查了带绝对值的化简.
【练习32】已知多项式3xn?2 ? 2xn ? 4xn?3 ? 3xn?1 ( n 是大于3 的整数)是八次四项式,试确定下列各单项式的次数与系数:(1) ?n ? 3? xn y ;(2) ?n ? 3? xn?1 yn?2 .
【难度】★
【答案】(1)次数:6,系数:2; (2)次数:9,系数:8.
【解析】解:由题意可得, n ? 3 ? 8,则n ? 5 ,所以⑴中代入可得: ?n ? 3? xn y ? 2x5 y ,所以次数为 6,系数为 2;代入⑵中可得?n ? 3? xn?1 yn?2 ? 8x6 y3 ,所以次数为 9,系数为 8.
【总结】本题炸药考查了单项式和多项式的次数和系数相关知识点.
【练习33】如果单项式2mx a y 与?5nx2a ?3 y 是关于 x、y 的单项式,且它们是同类项.
(1)求?7a ? 22?2016 的值.(2)若2mxa y ? 5nx2a?3 y ? 0 ,且 xy ? 0 ,求?2m ? 5n?2003 的值.
【难度】★★
【答案】(1) 1; (2)0.
【解析】解:它们是同类项,可得a ? 2a ? 3 ,解得: a ? 3 , 代入(1)中得: ?7a ? 22?2016 ? ??1?2016 ? 1 ;
(2)因为2mxa y ? 5nx2a?3 y ? 0 ,且 xy ? 0 ,所以2m ? 5n , 代入可得?2m ? 5n?2003 ? 02003 ? 0 .
【总结】本题主要考查同类项的知识点,同时考查奇负偶正的问题.
【练习34】计算:
(1) ?3x2 ? 2x ? 1?? ?x2 ? x ? 3?; (2) ?a ? b ? 2c??a ? b ? 2c? ;
(3) ??a? 2 ???a3 ?? ??a? ? ??a2 ?3 ? ??a3 ?2 ; (4)??2x2 y ? 6x3 y4 ? 8xy ?? ??2xy ? ;
? 3 1 1
? ? 1 ?2
(5) ? a4b7 ? a3b8 ?
a2b6 ? ? ? ? ab3 ? .
? 4 2 9
? ? 3 ?
【难度】★★
【答案】(1) 2x2 ? x ? 2 ;(2) a2 ? b2 ? 2ab ? 4c2 ;(3) ?a6 ;(4) x ? 3x2 y3 ? 4 ;
(5) 27 a2b ? 9 ab2 ?1. 4 2
【解析】(1)原式? 3x2 ? 2x ?1? x2 ? x ? 3 ? 2x2 ? x ? 2 ;
(2)原式? ?a ? b?2 ? 4c2 ? a2 ? b2 ? 2ab ? 4c2 ;
(3)原式? a6 ? a6 ? a6 ? ?a6 ;
(4)原式= (?2x2 y) ? (?2xy) ? 6x3 y4 ? (?2xy) ? (?8xy) ? (?2xy)
= x ? 3x2 y3 ? 4 ;
(5)原式? 3 a4b7 ? 1 a2b6 ? 1 a3b8 ? 1 a2b6 ? 1 a2b6 ? 1 a3b6
4 9 2 9 9 2
? 27 a2b ? 9 ab2 ?1 .
4 2
【总结】本题主要考查了整式的基本运算,注意相关法则的准确运用.
【练习35】先化简,再求值: ??2x2 ? (x ? y)(x ? y)?? ??(?x ? y)(?x ? y) ? 2 y2 ?? ,其中 x ? 1 ,
y ? ?2 .
【难度】★★
【答案】25
【解析】原式 ? ??2x2 ? x2 ? y2 ?? ??x2 ? y2 ? 2 y2 ??
? ?x2 ? y2 ??x2 ? y2 ? ? ?x2 ? y2 ?2 .
141076644913x ? 1,y ? ?2 ,?原式 ? (1 ? 4)2 ? 25 .
【总结】本题主要考查多项式的化简求值.
【练习36】解不等式: 2x ? (5 ? x)(x ?1) ? x(x ?1) ? 4 .
【难度】★★
【答案】 x ? ?9 .
【解析】解: 2x ? ?5x ? 5 ? x2 ? x?? x2 ? x ? 4
2x ? 4x ? x 2 ?5 ? x2 ? x ? 4
-x ? 9
x ? ?9
【总结】本题主要考查多项式的计算与不等式的结合.
【练习37】解方程: (x ? 3)(x ? 3) ? (2x ?1)(x ? 7) ? x2 .
【难度】★★
【答案】 x ?? 2 .
13
【解析】解: x2 ? 9 ? 2x2 ?14x ? x ? 7 ? x2
x2 ? 9 ? 2x2 ?13x ? 7x2
13x ? ?2
x ?? 2
13
【总结】本题结合了多项式和方程,同时考查学生的应变能力.
【练习38】计算: ?1 ? 1 ??1 ? 1 ??1 ? 1 ? ? ? ? ?1 ?
??
1 ? .
? 22 ?? 32 ?? 42 ? ?
202 ?
【难度】★★
【答案】 21 .
40
? ?? ?? ? ? ?
【解析】解: 原式 ? ?1 ? 1 ??1 ? 1 ??1 ? 1 ??1 ? 1 ???1 ?
???
1 ??1 ? 1 ?
?
? 2 ??
2 ??
3 ??
3 ? ?
20 ??
20 ?
? ?? ?? ?? ? ? ?? ?
? 1 ? 5 21
2 4 20
? 1 ? 21
2 20
? 21
40
【总结】本题主要考查平方差公式的灵活运用.
【练习39】试证明:
(1) 22005 ? 22004 ? 22003 能被5 整除;
(2)若n 是正整数,试说明3n?3 ? 4n?1 ? 3n?1 ? 22n 能被10 整除.
【难度】★★
【答案】略.
【解析】(1) 原式? 2222003 ? 2 ? 22003 ? 22003 ? 6 ? 22003 ? 22003 = 5 ? 22003 ,
所以能被 5 整除;
(2) 原式 ? ?3n?3 ? 3n?1 ?? ?4n?1 ? 22n ? ? ?32 ? 3n ?1 ? 3n ?1 ?? ?4n ?1 ? 4n ?
? 10 ? 3n?1 ? 5 ? 4n
所以能被 10 整除.
? 10 ? 3n?1 ?10 ? 22n?1 ,
【总结】能被某数整除的数可以分解成该数乘以另外一个数或式子.
【练习40】计算:
(1)已知9m ? 27m?1 ? 32m ? 27 ,求m 的值.
? 8 ?
4
(2)已知?16x2 ?3 ? ? 1 ?
? ?
? 5 ,求 x12 的值.
(3)已知2n ? a , 3n ? b ,求4n ? 6n ? 9n 的值.
(4)已知2a ? 3 , 2b ? 6 , 2c ? 12 ,求a、b、c 之间的一个数量关系式.
(5)比较大小: 244 , 333 , 422 .
【难度】★★
【答案】(1) m ? 2 ;(2) 25 ;(3) a2 ? ab ? b2 ;(4) 2b ? a ? c ;(5) 333 ? 422 ? 244 .
【解析】解:(1)因为9m ? 27m?1 ? 32m ? 27 ,所以32m ? 33m?3 ? 32m ? 33 ,即33m?3 ? 33 , 所以3m ? 3 ? 3 ,所以m ? 2 ;
1544751105041 4 12
(2) ?16x2 ?3 .? 1 ? ? 5 ,?24 x2 ?3 .? 1 ?
?
? 5 ,
8 2
? ? ? ?
? ? ? ?
? x6 ? 5,? x12 ? ?x6 ?2 ? 52 ? 25 .
1544751104661(3) 2n ? a ,3n ? b ,?4n ? 6n ? 9n ? ?22 ?n ? ?2 ? 3?n ? ?32 ?n ? a2 ? ab ? b2 ;
154475048088(4) 2a ? 3,2b ? 6 ,2c ? 12 ,?2a ? 2c ? 2a?c ? 3?12 ? 36 ,2b ? 2b ? 22b ? 6 ? 6 ? 36 ,
所以2b ? a ? c .
(5)观察发现, 244 ? ?24 ?11 ? 1611 ,333 ? ?33 ?11 ? 2711 ,422 ? ?42 ?11 ? 1611 ,因为1611 ? 2711 ,所以333 ? 244 ? 422 .
【总结】本题主要考查了幂的运算,以及比较大小.比较大小时,要么化成底数相同,比较
指数大小,要么化成指数相同,比较底数大小.
【练习41】如果?x ? a??x ? 4? ?1能够分解成两个多项式 x ? b 、x ? c 的乘积( b、c 为整数),求 a 的值.
【难度】★★
【答案】a ? 4 .
【解析】解:因为?x ? a??x ? 4??1 ? x2 ? ?a ? 4?x ? 4a ? 1,
又 ?x ? b??x ? c? ? x2
??? ?4 ? a? ? b ? c
? ? ? ? ? ,所以
b c x bc ?
??4a ?1 ? bc
,则?4b ? 4c ?17 ? bc ,
整理可得: ?b ? 4??c ? 4? ? ?1
,因为 b、c 为整数,所以 b、c 一个取-3,一个取-5,
代入得a ? 4 .
【总结】本题要注意后面的解题思路,利用 b、c 为整数这个条件,可以得出最后的结果.
【练习42】已知?a ? b?2 ? 12 , ?a ? b?2 ? 3 ,求:(1) ab ;(2) a2 ? b2 ;(3) a2 ? b2 的值.
【难度】★★
【答案】(1) 9 ;(2) 15 ;(3) ?6 .
4 2
【解析】解:由题意可得, ?a ? b?2 ? a2 ? 2ab ? b2 ? 12 ,?a ? b?2 ? a2 ? 2ab ? b2 ? 3 ,
所以(1)中求ab ,两式相减可得: 4ab ? 9 ,ab ? 9 ;
4
2
(2)两式相加可得: 2?a2 ? b2 ?? 15,则a2 ? b2 ? 15 ;
(3)因为a2 ? b2 ? ?a ? b??a ? b?,所以?a ? b?2 ? ?a ? b?2 ? 12 ? 3 ? 36 ,所以?a ? b?? ?a ? b? ? ?6 .
【总结】本题主要考查平方差公式和完全平方公式的综合运用.
【练习43】已知多项式 A 除以4x3 ? 3x2 ?1 得商式3x2 ? 3x ,余式 x2 ?1 ,求多项式 A .
【难度】★★
【答案】 A ? 12x5 ? 21x4 ? 9x3 ? 2x2 ? 3x ?1.
【解析】解:由题意可知,商×除式+余式=被除式,
所以 A ? (3x2 ? 3x) ? (4x3 ? 3x2 ?1) ? x2 ?1 ? 12x5 ? 21x4 ? 9x3 ? 2x2 ? 3x ?1 .
【总结】该题实际还是考查多项式×多项式的计算,同时有方程的思想在里面.
1 1 ? 1 ?2 1
【练习44】已知 x ? ? 3 ,求:(1) x2 ? ;(2) ? x ? ? ;(3) x4 ? 的值.
x x2 ? x ? x4
【难度】★★
【答案】(1)7;(2)5;(3)47.
1 ?
1 ?2 1 1
【解析】解:(1)因为 x ? ? 3,所以? x ? ? ? x2 ? ? 2 ? 9 ,所以x2 ? ? 7 ;
x ? x ? x2 x2
? 1 ?2 ? 1 ?2
? 1 ?2
(2)因为? x ? x ? ? ? x ? x ? ? 4 ,所以? x ? x ?
? 9 ? 4 ? 5 ,
? ? ? ? ? ?
1 ? 1 ?2 1 1
(3)由(1)知 x2 ? ? 7 ,所以? x2 ? ? ? x4 ? ? 2 ? 49 ,所以x4 ? ? 47 .
x2 ? x2 ? x4 x4
【总结】本题主要考查两个互为倒数的数的平方的规律,中间项为常数项.
【练习45】分解因式:
(1) ?x ? 2??x ? 4? ? x2 ?16 ; (2) 4m2 ?x ? y?3 ? ? y ? x?3 ?m ? n?2
(3)16a4 ? 72a2 ? 81; (4)?x ? 5y?2 ? (2x ?10 y)(3x ? y) ? ?3x ? y ?2 ;
(5) ?x2 ? x?2 ?18?x2 ? x?? 72 ; (6) a4 ? a2 ? 4a ? 4 ;
(7) ?x2 ? x ? 1??x2 ? x ? 2??12 .
【难度】★★
【答案】(1) 2?x ? 4??x ?1? ;(2) ?x ? y?3 ?3m ? n??m ? n? ;(3) (2a ? 3)2 (2a ? 3)2 ;
(4)16?x ? y ?2 ;(5) ?x ? 3??x ? 2??x ? 4??x ? 3? ;(6) ?a ? 2??a ?1??a2 ? a ? 2? ;
(7) ?x2 ? x ? 5??x ? 2??x ?1?.
【解析】解:(1)原式= ?x ? 2??x ? 4? ? ?x ? 4??x ? 4? ? ?x ? 4??x ? 2 ? x ? 4? ? 2 ?x ? 4??x ? 1? ;
? ?
(2)原式= ?x ? y ?3 ?4m2 ? ?m ? n?2 ? ? ?x ? y ?3 ?2m ? m ? n??2m ? m ? n?
? ?x ? y?3 ?3m ? n??m ? n? ;
(3)原式= ?4a2 ? 9?2 ? (2a ? 3)2 (2a ? 3)2 ;
(4)原式= ?x ? 5y?2 ? 2(x ? 5y)(3x ? y) ? ?3x ? y?2 ? ?x ? 5y ? 3x ? y?2
? ?4x ? 4 y?2 ? 16?x ? y?2 ;
(5)原式= ?x2 ? x ? 6??x2 ? x ? 12?? ?x ? 3??x ? 2??x ? 3??x ? 4? ;
(6)原式= a4 ? ?a2 ? 4a ? 4?? a4 ? ?a ? 2?2
? ?a2 ? a ? 2??a2 ? a ? 2?? ?a ? 2??a ?1??a2 ? a ? 2?;
(7)原式? ?x2 ? x?2 ? 3(x2 ? x) ?10 ? (x2 ? x ? 5)(x2 ? x ? 2)
? (x2 ? x ? 5)(x ? 2)(x ?1) .
【总结】本题主要考查因式分解,一定要分解到不能再分解为止.
【练习46】已知多项式 x2 ? xy ? 12 y2 ,(1)将此多项式因式分解;(2)若多项式 x2 ? xy ? 12 y2
的值等于?6 ,且 x、y 都是整数,求满足条件的 x、y 的值.
【难度】★★
? ? ?
【答案】(1) ?x ? 4 y ??x ? 3y ? ;⑵ ?x ? 3, ?x ? 2
, ?x ? ?3, ?x ? ?2
?
? y ?
1 ? y ? ?1 ? y ? ?1 ? y ? 1
【解析】解:(1)将原式因式分解= ?x ? 4 y ??x ? 3y ? ;
174477676692(2) x2 ? xy ?12y2 ? ?x ? 4y??x ? 3y?,??x ? 4y??x ? 3y? ? ?6 ,
则有?6 ? ??1?? 6 ? ??6??1 ? ??2?? 3 ? ??3?? 2 ,又 x ? 3y ? ?x ? 4y
?? 7y
,所以两个数相
减一定是 7 的倍数,则只能去-1 和 6,或者-6 和 1 这两组,所以有
?x ? 4 y ? ?1
?x ? 4 y ? 6
?x ? 4 y ? 1
?x ? 4 y ? ?6
① ?x ? 3y ? 6 ,② ?x ? 3y ? ?1,③ ?x ? 3y ? ?6 ,④ ?x ? 3y ? 1 ,
? ? ? ?
分别解可得: ?x ? 3
?x ? 2
?x ? ?3
?x ? ?2 .
? ? ? ?
? y ? 1 ,? y ? ?1,? y ? ?1,? y ? 1
【总结】本题不仅仅考查因式分解,还考查了分类讨论的思想.
【练习47】已知2x2 ? 3x ? 4 ? a ?x ?1?2 ? b ?x ?1? ? c ,求a 、b 、c 的值.
【难度】★★
【答案】a ? 2,b ? 7 ,c ? 9 .
【解析】右边的多项式展开= ax2 ? ?b ? 2a? x ? ?a ? b ? c?,对应未知数的系数相等可得,
?a ? 2 ?a ? 2
? ?
?b ? 2a ? 3
?a ? b ? c ? 4
,所以解得:?b ? 7 .
?c ? 9
? ?
【总结】本题中两个多项式相等,则对应的系数也相等.
【练习48】已知 x ? y ,且 x2 ? x ? 2 , y2 ? y ? 2 ,求代数式 x2 ? xy ? y2 .
【难度】★★★
【答案】7.
194416685597【解析】解:
x2 ? x ? 2 ,x2 ? x ? 2 ? 0 ,??x ? 2??x ?1? ? 0 ,解得: x ? 2或x ? ?1 ,
同理可解得: y ? 2或y ? ?1 ,因为 x ? y ,所以一个取 2,一个取-1,代入可得:
x2 ? xy ? y2 ? 22 ? 2 ? 12 ? 7 .
【总结】本题要利用因式分解解出 x、y 的取值,再代入.
【练习49】计算: ?2 ? 1??22 ? 1??24 ? 1??28 ? 1?? ? ? ?232 ? 1?.
【难度】★★★
【答案】264 ?1 .
425250995953【解析】解:原式? ?2 ?1??2 ? 1??22 ? 1??24 ? 1??28 ? 1? ?232 ? 1?
3692222176247? ?22 ?1??22 ? 1??24 ? 1??28 ? 1? ?232 ? 1?
3279632177517? ?24 ?1??24 ? 1??28 ? 1? ?232 ?1?
? 264 ? 1 .
【总结】本题很灵活的运用平方差公式解题,同时考查学生的观察能力.
【练习50】若 A ? ?3 ? 1??32 ? 1??34 ? 1??38 ? 1??316 ? 1??332 ? 1??364 ? 1? ,求 A ? 2002 的末位数字.
【难度】★★★
【答案】末尾数是 5
2
【解析】解:A ? 1 (3 ?1) ?3 ?1??32 ?1??34 ?1??38 ?1??316 ?1??332 ?1??364 ?1?
2
? 1 (32 ?1)?32 ?1??34 ?1??38 ?1??316 ?1??332 ?1??364 ?1?
? 1 (3128 ?1) ,
2
400707145158因为31 ? 3,32 ? 9 ,33 ? 27 ,34 ? 81,35 ? 243
,由此可见,每四个末尾数就开始重复
3、9、7、1,128 ? 4 ? 32 ,所以3128 的末尾数是 1,减去 1 后,末尾数是 0,再×0.5 , 末尾数就是 5.
【总结】本题主要考查的是学生的分析能力和观察能力,是否能找到隐藏的规律.
【练习51】已知a2 ? 2a ? b2 ? 6b ?10 ? 0 ,求a2 ? b2 的值.
【难度】★★★
【答案】10.
【解析】解:由题意可得: a2 ? 2a ?1 ? b2 ? 6b ? 9 ? ?a ? 1?2 ? ?b ? 3?2 ? 0 ,
? ?
所以有?a ? 1 ? 0 ,? ?a ? ?1 ,代入后有a2 ? b2 ? 1? 9 ? 10 .
?b ? 3 ? 0 ?b ? 3
【总结】本题主要考查了配方法的运用,还是非负数之和为 0 的情况.
【练习52】证明:四个连续整数的乘积加1是整数的平方.
【难度】★★★
【答案】略.
【解析】证明:设四个连续整数为n, n ? 1, n ? 2, n ? 3 ,则有
n ?n ? 1??n ? 2??n ? 3? ? 1
? ?n2 ? 3n??n2 ? 3n ? 2?? 1
? ?n2 ? 3n?2 ? 2?n2 ? 3n?? 1
? ?n2 ? 3n ? 1?2
【总结】本题要注意两两组合,把相同的部分n2 ? 3n 看成一个整体,再进行完全平方.
同课章节目录
