沪教版七年级秋季班第18讲:中心对称与轴对称教师版
文档属性
| 名称 | 沪教版七年级秋季班第18讲:中心对称与轴对称教师版 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-21 17:04:43 | ||
图片预览



文档简介
-4159258890中心对称与轴对称
中心对称与轴对称
-142875245110内容分析
内容分析
理解两个图形关于某一点中心对称的意义.能够区分中心对称与中心对称图形.掌握轴对称、轴对称图形的概念,知道轴对称与轴对称图形区别,会利用有关性质画出已知图形关于某一条直线对称的图形.重点理解相关概念,能够判断出图形特点.
-18097560960 知识结构
知识结构
7766051769745模块一:中心对称
模块一:中心对称
-79375104775知识精讲
知识精讲
中心对称的概念
把一个图形绕着一个定点旋转180°后,和另一个图形重合,那么叫做这两个图形关于这点对称,也叫做这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点.
中心对称图形的特征
中心对称是旋转对称的特例,关于中心对称的两个图形能完全重合.关于中心对称的两个图形,对称点的连线都经过对称中心并且被对称中心平分,关于对称中心的两个图形,对应线段平行(或在一条直线上)且相等;反过来,如果两个图形的对应点连接成的线段都经过某一点并且被该点平分,那么这两个图形一定关于这点成中心对称,这给我们提供了判断某两个图形是否成中心对称的方法.
3、中心对称与中心对称图形的区别与联系
中心对称是两个图形而言的,指两个图形间的关系;而中心对称图形是对一个图形而言的,指一个图形的两个部分之间的关系.成中心对称的两个图形的对称点分别在两个图形上,中心对称图形的对称点在一个图形上.若把中心对称图形的两个部分看成两个图形,则它们成中心对称,若把中心对称的两个图形看作一个整体,则成中心对称图形.
-21272573025例题解析
例题解析
下列图案都是由字母“”经过变形、组合而成的.其中不是中心对称图形的是
( ).
A B C D
【难度】★
【答案】
【解析】根据中心对称图形的概念可知,均是中心对称图形.
【总结】本题考查了中心对称图形的定义.
在下列四个汽车标志图案中,是中心对称图形的是( )
A B C D
【难度】★
【答案】
【解析】根据中心对称图形的概念可知,中心对称图形是图形沿对称中心旋转后与原 图重合,故选.
【总结】本题考查了中心对称图形的定义.
关于中心对称的两个图形所有对应点的连线________交于一点.
(填“一定”、“不一定”)
【难度】★
【答案】一定.
【解析】关于中心对称的两个图形,对应点的连线必过对应中心.
【总结】本题考查了中心对称的性质.
请写出两个是中心对称图形的汉字_________.
【难度】★
【答案】日、田等.
【解析】中心对称图形是图形沿对称中心旋转后与原图重合.
【总结】本题考查了中心对称的应用.
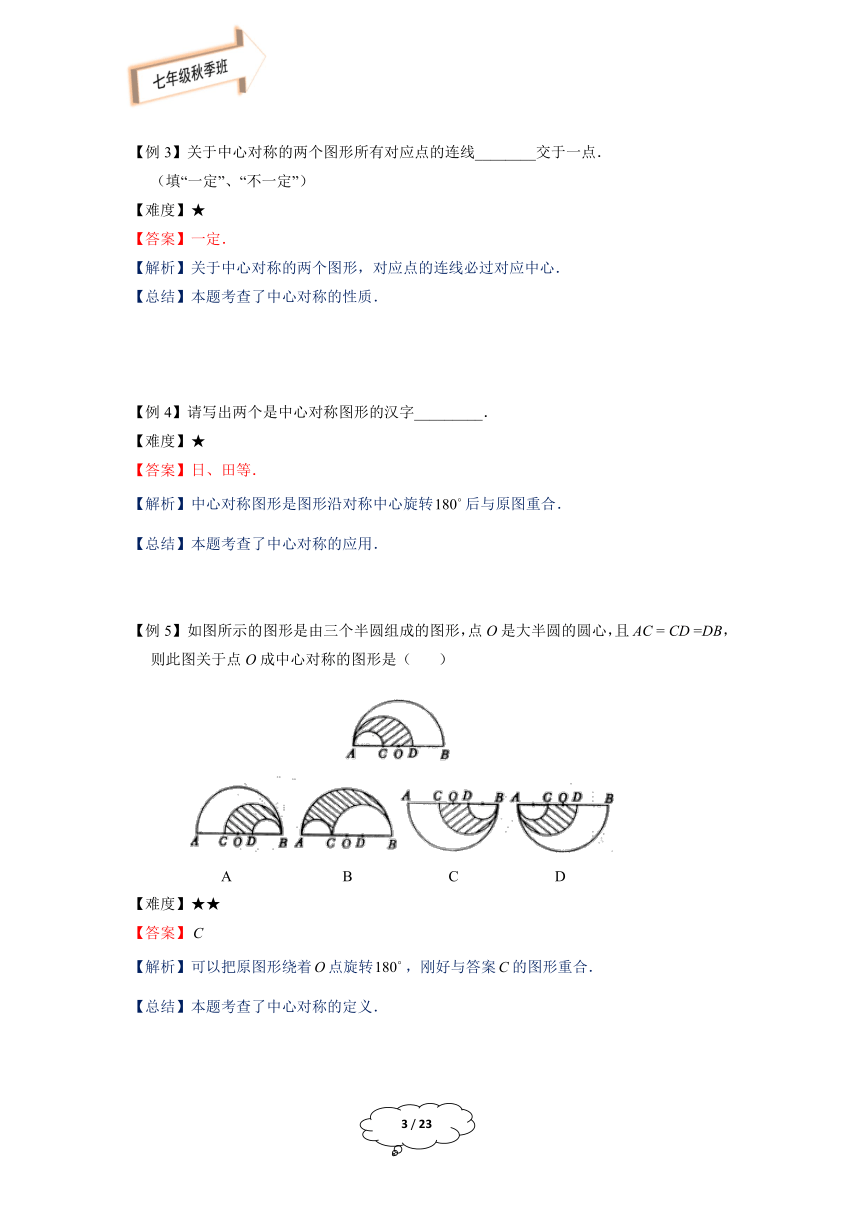
如图所示的图形是由三个半圆组成的图形,点O是大半圆的圆心,且AC = CD =DB, 则此图关于点O成中心对称的图形是( ?????)
A B C D
【难度】★★
【答案】
【解析】可以把原图形绕着点旋转,刚好与答案的图形重合.
【总结】本题考查了中心对称的定义.
(1)线段;(2)两条相交直线;(3)角;(4)等腰三角形;(5)等边三角形;(6) 平行四边形;(7)矩形;(8)菱形;(9)正方形;(10)圆;(11)等腰梯形等图形中是 中心对称图形的是______________________.(填序号)
【难度】★★
【答案】(1),(6),(7),(8),(9),(10)
【解析】常见中心对称图形:矩形、菱形、正方形、平行四边形、圆、线段、正偶边形等.
【总结】本题考查了常见中心对称图形,注意直线不是轴对称图形.
若两个图形关于某点成中心对称,则下列说法中,正确的有( )个.
对应线段相等;②对应角相等;③周长相等;④面积相等.
A.1 B.2 C.3 D.4
【难度】★★
【答案】
【解析】中心对称的性质:对应角相等、对应线段相等、两个图形全等.
【总结】本题考查了中心对称的性质.
请画出△ABC关于点O成中心对称的对称图形.
【难度】★★
【答案】见解析
【解析】依次连结,并延长到,使得
,连结即为所求图形.
所以为所求.
【总结】本题考查了作中心对称图形,注意找关键点.
10561320238125
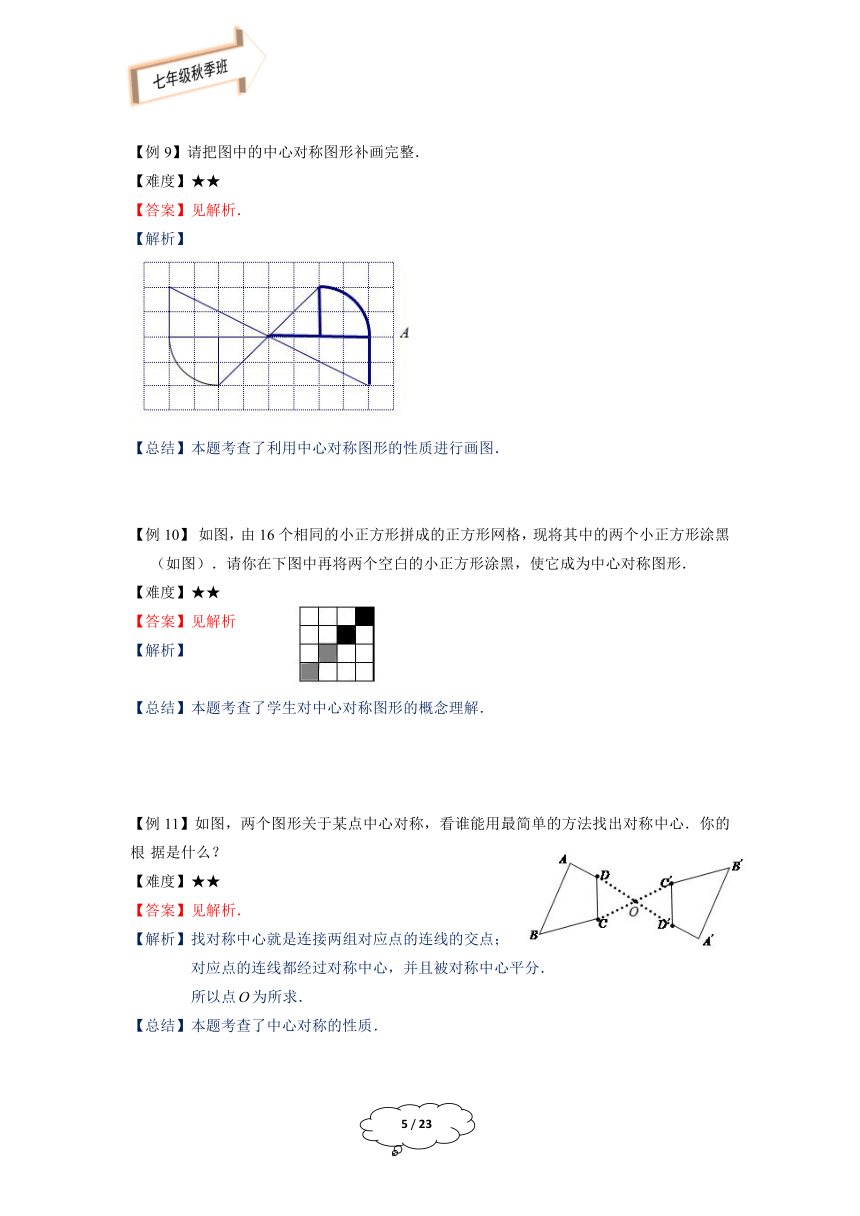
请把图中的中心对称图形补画完整.
【难度】★★
【答案】见解析.
【解析】
【总结】本题考查了利用中心对称图形的性质进行画图.
?如图,由16个相同的小正方形拼成的正方形网格,现将其中的两个小正方形涂黑 (如图).请你在下图中再将两个空白的小正方形涂黑,使它成为中心对称图形.
133350016637000【难度】★★
【答案】见解析
【解析】
【总结】本题考查了学生对中心对称图形的概念理解.
330200022479000如图,两个图形关于某点中心对称,看谁能用最简单的方法找出对称中心.你的根 据是什么?
【难度】★★
【答案】见解析.
【解析】找对称中心就是连接两组对应点的连线的交点;
对应点的连线都经过对称中心,并且被对称中心平分.
所以点为所求.
【总结】本题考查了中心对称的性质.
请你用剪刀剪去等边三角形三个角,使余下的部分成为一个中心对称图形,应该怎 样剪?
【难度】★★★
【答案】见解析.
【解析】如图所示正六边形为中心对称图形.(做等边三角形的三等分点即可)
【总结】本题考查了中心对称图形的知识.
如图:已知矩形ABCD的两边AB = 4厘米,BC =12厘米
(1)在图1中画出矩形ABCD的对称中心.(不写结论)
(2)动点P从点A出发,以每秒2厘米的速度沿AD边向点D移动,动点Q同时从点B 出发,以每秒1厘米的速度沿BC边向点C移动 ,联结PQ得图2 .
问:①当P、Q出发几秒后,梯形ABQP的面积是梯形PQCD面积的两倍;
127635019939000当P、Q出发几秒后,图2是一个中心对称图形.
【难度】★★★
【答案】见解析.
【解析】(1)如图1;
(2)解:设运行的时间为秒钟,则,.
①,
,化简得:,解得:.
当出发秒钟后,梯形的面积是梯形面积的两倍.
②由题意得, ,即.
当出发秒后,图2是一个中心对称图形.
【总结】本题考查了中心对称图形的应用.
-922020172720模块二:轴对称
模块二:轴对称
-198120121285知识精讲
知识精讲
1、翻折与轴对称图形
(1)把一个图形沿一条直线翻折过来,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,两个图形中的对应点叫做关于这条直线的对称点.
(2)轴对称图形是一个图形关于某直线对称;轴对称是两个图形关于某条直线对称.
2、轴对称
(1)轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么称这两个图形关于这条直线对称,也称这两个图形成轴对称.
(2)轴对称的图形的性质:两个图形关于一条直线成轴对称,这两个图形对应线段的长度和对应角的大小相等,它们的形状相同,大小不变;在成轴对称的两个图形中,分别连接两对对应点,取中点,连接两个中点所得的直线就是对称轴.
-20002593345例题解析
例题解析
下列几何图形中,①线段;②角;③圆;④等腰三角形;⑤直角三角形;其中是轴 对称图形的有( )
A.1个 B.2个 C.3个 D.4个
【难度】★
【答案】
【解析】把一个图形沿一条直线翻折过来,直线两旁的部分能够互相重合,这个图形叫做轴 对称图形.
【总结】本题考查了常见的轴对称图形.
下列图形中对称轴最多的是( )
A.圆 B.正方形 C.等腰三角形 D.线段
【难度】★
【答案】
【解析】圆有无数条对称轴;正方形有4条对称轴;等腰三角形有1条对称轴;线段有2 条对称轴.
【总结】本题考查了轴对称图形的对称轴.
下列图案中是轴对称图形的是( )
2008年北京 2004年雅典 1988年汉城 1980年莫斯科
2008年北京 2004年雅典 1988年汉城 1980年莫斯科
A B C D
【难度】★
【答案】
【解析】把一个图形沿一条直线翻折过来,直线两旁的部分能够互相重合,这个图形叫做轴 对称图形.
【总结】本题考查了对生活中的轴对称图形的辨识.
作出下图所示的图形的对称轴:
1238250969010
【难度】★
【答案】见解析.
【解析】
【总结】本题考查了对称轴的画法.
正六边形是轴对称图形,它有 条对称轴.
【难度】★
【答案】
【解析】正六边形有6条对称轴,分别是3条对角线所在直线及3组对边的垂直平分线.
【总结】本题考查了轴对称图形的对称轴的个数.
在下列四种图形变换中,本题图案不包含的变换是( )
中心对称;②旋转;③轴对称; ④平移 .
A.①② B.②③ C.③④ D.①④
226695013970000
【难度】★★
【答案】
【解析】图形的方向发生了改变,不符合平移;绕定点旋转后,图形不能与自身重合, 故不含中心对称.
【总结】本题考查了中心对称、旋转、轴对称、平移的特点.
107950502920将一圆形纸片对折后再对折,得到图3-1中图3,然后沿着图中的虚线剪开,得到 两部分,其中一部分展开后的平面图形是(???? )?? ?
?
A B C D
【难度】★★
【答案】C
【解析】根据题意知,剪去的纸片一定是一个四边形,且对角线相互垂直,故选C.
【总结】本题考查了图形的变换,注意减掉的图形的特征.
3905250259080如图,和关于直线对称,且,,求的度 数和的长.
【难度】★★
【答案】.
【解析】如果两个图形关于某一直线成轴对称,则它们的对应线段
相等,对应角相等.所以.
【总结】本题考查了轴对称图形的性质.
280035022987000尺规:把右图(实线部分)补成以虚线为对称轴的轴对称图形,你会得到一只美 丽蝴蝶的图案(不用写作法、保留作图痕迹).
【难度】★★
【答案】见解析
【解析】
【总结】本题考查了利用轴对称设计图案.
如图,阴影部分是由5个小正方形组成的一个直角图形,请用两种方法分别在下图方格内添涂黑二个小正方形,使它们组成轴对称图形.(试用两种方法)
【难度】★★
【答案】见解析
【解析】
【总结】本题考查了利用轴对称设计图案
如图,等边的边长为a,、分别是、上的点,将沿 直线折叠,点落在点处,且点在外部,则阴影部分图形的周长为
3987800102870 ________________ .
【难度】★★
【答案】.
【解析】等边的边长为,,
沿直线折叠,点落在点处,
,
阴影部分的周长为
.
【总结】本题考查了简单图形的折叠问题.
如图,在公路的同旁有两个仓库、,现需要建一货物中转站,要求到、 两仓库的距离和最短,这个中转站应建在公路旁的哪个位置比较合理?
378460055880【难度】★★★
【答案】见解析
【解析】
作点关于直线的对称点,连接,交直线于点,点为所求.
【总结】本题考查了轴对称图形在实际问题中的应用.
317500048895000打台球问题,在一个长方形球台ABCD上,点P、点Q各放着一个球,现在要求 点P的球先碰AB边,反弹BC边,最后反弹碰到Q的球.问点P的球应该撞击AB的哪 一点,才能够达到上述要求?
【难度】★★★
【答案】见解析.
【解析】在边的另一侧作出点的对称点,
在的另一侧作出的对称点,
连接,所得直线与的交点F,即为点的球应该撞击的位置.
【总结】本题考查了图形的对称问题,综合性较强,注意认真分析.
2686050121793000地面上有不共线的三点A、B、C,一只青蛙位于异于A、B、C的点P.第一步, 青蛙从P点跳到关于A的对称点;第二步,青蛙从跳到关于B的对称点;第三 步,青蛙从跳到关于C的对称点;第四步,从跳到关于A的对称点;…,如 此不断地跳下去,问青蛙跳完6666步后落在什么位置上?
【难度】★★★
【答案】见解析
【解析】由图可知:,
两对角相等,平行且等于,
如果有,则同样可得平行且等于,平行且等于,
构成一个三角形,同理也构成一个三角形,两个三角形中两个边分别平行 且相等,可证明另一边平行且相等,这样就可以证明与重合,即就是, 则每6步是一个轮回,故6666步落于点.
【总结】本题考查了图形的对称规律,注意认真分析.
-1743075113665随堂检测
随堂检测
下列“表情”中属于轴对称图形的是( )
A B C D
【难度】★
【答案】
【解析】把一个图形沿一条直线翻折过来,直线两旁的部分能够互相重合,这个图形叫做轴 对称图形.
【总结】本题主要考查了简单的轴对称图形的判断.
下列交通标志中,不是轴对称图形的是( )
A B C D
【难度】★
【答案】
【解析】把一个图形沿一条直线翻折过来,直线两旁的部分能够互相重合,这个图形叫做轴 对称图形.
【总结】本题考查了简单的轴对称图形.
下列图形中,是中心对称图形的是( )
A B C D
【难度】★
【答案】
【解析】根据中心对称图形的概念可知,中心对称图形是图形沿对称中心旋转后与原 图重合.
【总结】本题考查了中心对称图形的概念.
正2n边形,有______条对称轴,它有________个对称中心.
【难度】★
【答案】;1.
【总结】本题考查了轴对称图形的定义及对称轴的条数.
下列图案中,既是轴对称图形,又是中心对称图形的是(?? )
A B C D
【难度】★★
【答案】
【解析】把一个图形沿一条直线翻折过来,直线两旁的部分能够互相重合,这个图形叫做轴 对称图形;中心对称图形是图形沿对称中心旋转后与原图重合.
【总结】本题考查了轴对称图形和中心对称图形的定义.
下列图案中,有且只有三条对称轴的是( )
A B C D
【难度】★★
【答案】
【解析】有两条对称轴;有四条对称轴;不是轴对称图形.
【总结】本题考查了轴对称图形的对称轴的条数.
1972945420370下面四个图形中,从几何图形的性质考虑,哪一个与其他三个不同?请指出这个 图形,并简述你的理由.
答:图形_______________;
理由是________________.
【难度】★★
【答案】②;只有②不是轴对称图形.
【解析】四个图形中,只有②不是轴对称图形,其余都是.
【总结】本题考查了几何图形的变换性质.
下列图形中,既是轴对称图形又是中心对称图形的是( )
A.等腰三角形 B.等腰梯形 C.正方形 D.平行四边形
【难度】★★
【答案】
【解析】是轴对称图形,但不是中心对称图形;是轴对称图形,但不是中心对称图形;
不是轴对称图形,但是中心对称图形.
【总结】本题考查了轴对称图形和中心对称图形的定义.
下列说法中错误的是( ).
A.圆有无数条对称轴,一个对称中心
B.等边三角形有三条对称轴,三个对称中心
C.正方形有四条对称轴,一个对称中心
D.等腰梯形仅有一条对称轴,没有对称中心
【难度】★★
【答案】
【解析】所有中心对称图形都只有一个对称中心;故错误.
【总结】本题考查了常见的轴对称图形特点.
349885021590000作出下图所示的成轴对称图形的对称轴:
1644650120650【难度】★★
【答案】
【解析】
【总结】本题考查了成轴对称图形对称轴的画法,主要是找出关键点.
如图,画出半圆A关于点F中心对称的图形.
2705100163830【难度】★★
【答案】见解析
【解析】
作半圆的直径的两外端点点关于点对称点,再画半圆.
【总结】本题考查了中心对称图形的画法.
2355850425450如图(1)(2)所示的两组长方形能否关于某一点成中心对称?若能,则请画出 其对称中心.
【难度】★★
【答案】见解析
222250015748000【解析】(1)能成中心对称;(2)不能.
如图(1)点为所求.
【总结】本题考查了中心对称的两个图形,对称中心的画法.
如图是由3个同样的小正方形所组成,请再补上一个同样的小正方形,使得由4 个小正方形组成的图形成为一个中心对称图形.要求:画出所有的情况,并且在所添画 的正方形中用数字标出.
【难度】★★★
【答案】见解析
【解析】共有三种情况.
【总结】本题考查了中心对称图形的定义.
如图跳棋盘,其中格点上的黑色点为棋子,剩余的格点上没有棋子.我们约定跳棋游戏的规则是:把跳棋棋子在棋盘内沿直线隔着棋子对称跳行,跳行一次称为一步.已
4044950228600知点为已方一枚棋子,欲将棋子跳进对方区域(阴影部分的格点),则跳行的最
少步数为(??? )
?????? A.2步????????????????? B.3步???????????????????C.4步????????????????? D.5步
【难度】★★★
【答案】
【解析】
【总结】本题考查了‘桌球问题’中的轴反射.
如图,,角内有点,且OP = 2,在角的两边有两点、(均不
3577590158750 同于点), 求作、,使得的周长的最小,并求出最小值.
【难度】★★★
71942027305000【答案】.
【解析】如图:
分别作关于的对称点,连接交于,则 符合条件,连接,则,的周长,
则,所以为等腰直角三角形,
.
【总结】本题考查了轴对称图形的性质及勾股定理的应用,综合性较强,注意认真分析.
-10604581280课后作业
课后作业
下面四个标志图是中心对称图形的是( )
476250163830A
B
C
D
A
B
C
D
【难度】★
【答案】
【解析】生活中的中心对称图形,参考中心对称图形定义.
【总结】本题考查了中心对称图形的定义.
正八边形________中心对称图形.(填“是”或“不是”).
【难度】★
【答案】是
【解析】因为将正八边形绕正八边形的中心旋转后能够与自身重合,所以为中心对称 图形.
【总结】本题考查了中心对称图形的定义.
圆______是中心对称图形,两个圆__________关于某点成中心对称.(填“一定”、 “不一定”或“一定不”)
【难度】★
【答案】一定;不一定.
【解析】圆是中心对称图形,因为不确定两个圆的大小,所以两个圆不一定关于某点成中心 对称.
【总结】本题考查了圆这个基本图形的中心对称性.
下列图形中,既是轴对称图形,又是中心对称图形的是( )
【难度】★
【答案】
【解析】是轴对称图形,但不是中心对称图形;是轴对称图形,但不是中心对称图形;
不是轴对称图形,但是中心对称图形.
【总结】本题考查了轴对称图形和中心对称图形的定义.
3571875336550如图,直线是四边形的对称轴,若,有下面的结论:①; ②; ③; ④,其中正确的结论有_______.
【难度】★★
【答案】①②③.
【解析】解:轴对称图形的两部分是全等的,所以①②③正确.
【总结】本题考查了轴对称图形的性质.
如图所示,将一张正方形纸片对折两次,然后在上面打个洞,则纸片展开后 是 .
(1) (2) (3) (4)
【难度】★★
【答案】
【解析】当正方形纸片两次沿对角线对折成为一直角三角形时,在平行于斜边的位置打3 个洞,则直角顶点处完好,则原正方形中间无损,且有12个洞.
【总结】本题考查了空间思维及折叠处理实际问题.
下图中②③④⑤分别由①图顺时针旋转180°变换而成的是____________.
?
① ② ③ ④ ⑤
【难度】★★
【答案】④.
【解析】根据中心对称图形的概念可知,中心对称图形是图形沿对称中心旋转后与原 图重合.
【总结】本题考查了中心对称图形的定义.
某校计划建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到的设
计方案有等边三角形、等腰梯形、菱形、正五边形等四种方案,你认为符合条件的是(??? )
???? A. 等边三角形??? ??? B.等腰梯形?? ???C.菱形????????? D. 正五边形
【难度】★★
【答案】.
【解析】等边三角形是轴对称图形,但不是中心对称图形;等腰梯形是轴对称图形,但不是 中心对称图形;正五边形是轴对称图形,但不是中心对称图形.
【总结】本题考查了基本图形的特性.
3365500654050两个完全一样的三角形,可以拼出各种不同的图形,如图已画出其中一个三角形, 请你分别补画出另一个与其一模一样的三角形,使每个图形分别构成不同的中心对称 图形(所画三角形可与原三角形有重叠部分).
?【难度】★★
【答案】
180213015240000【解析】
330835023241000
370205021590000172085018478500-2413008255000
【总结】本题考查了中心对称图形的定义及画图.
在由小正方形组成的形的图中,用三种不同方法添画一个小正方形,使它成为 轴对称图形.
方法一 方法二 方法三
【难度】★★★
【答案】见解析
【解析】
【总结】本题考查了轴对称图形的性质.
菱形ABCD的两条对角线AC、BD互相垂直平分,相交于点O,O就是它的对 称中心,过它的顶点A、D向BC及其延长线作垂线AE、DF,E、F为垂足,图中的三 角形可以看作
(1)由平移变换得到的有_________对,它们是__________;
309499031750 (2)由旋转变换得到的有_________对,它们是__________;
(3)由翻折变换得到的有_________对,它们是__________.
【难度】★★★
【答案】见解析
【解析】(1)由平移变换得到的有对,为;
(2)由旋转变换得到的有对,
为、、
、;
(3)由翻折变换得到的有对,为
.
【总结】本题考查了图形的几种变换,注意每种变换的特征.
已知:、两点在直线的同侧,在上求作一点,使得最大.
34544006985【难度】★★★
【答案】见解析
【解析】
连接与的交点即为,根据三角形两边之差小于第三边.
【总结】本题考查了图形最值问题的实际操作问题.
两个人轮流在一张圆心桌面上摆放硬币,规则是每人每次摆一枚,硬币不能互相 重叠,也不能有一部分在桌面的边缘之外,摆好之后不许再移动,这样经过多次摆放, 直到谁最先摆不下硬币谁就认输,按照这个规则,你用什么方法才能保证取胜?
【难度】★★★
【答案】争取先放,并且把第1枚硬币放在桌面的对称中心上.
【解析】你要争取先放,并且把第1枚硬币放在桌面的对称中心上,以后你应该根据对方所
放硬币的位置,在它关于中心对称的位置上放下一枚同样大小的下一枚硬币,你就能保
证在其对称位置上放下一枚同样大小的硬币,即可.
【总结】本题考查了中心对称的性质运用.
中心对称与轴对称
-142875245110内容分析
内容分析
理解两个图形关于某一点中心对称的意义.能够区分中心对称与中心对称图形.掌握轴对称、轴对称图形的概念,知道轴对称与轴对称图形区别,会利用有关性质画出已知图形关于某一条直线对称的图形.重点理解相关概念,能够判断出图形特点.
-18097560960 知识结构
知识结构
7766051769745模块一:中心对称
模块一:中心对称
-79375104775知识精讲
知识精讲
中心对称的概念
把一个图形绕着一个定点旋转180°后,和另一个图形重合,那么叫做这两个图形关于这点对称,也叫做这两个图形成中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点.
中心对称图形的特征
中心对称是旋转对称的特例,关于中心对称的两个图形能完全重合.关于中心对称的两个图形,对称点的连线都经过对称中心并且被对称中心平分,关于对称中心的两个图形,对应线段平行(或在一条直线上)且相等;反过来,如果两个图形的对应点连接成的线段都经过某一点并且被该点平分,那么这两个图形一定关于这点成中心对称,这给我们提供了判断某两个图形是否成中心对称的方法.
3、中心对称与中心对称图形的区别与联系
中心对称是两个图形而言的,指两个图形间的关系;而中心对称图形是对一个图形而言的,指一个图形的两个部分之间的关系.成中心对称的两个图形的对称点分别在两个图形上,中心对称图形的对称点在一个图形上.若把中心对称图形的两个部分看成两个图形,则它们成中心对称,若把中心对称的两个图形看作一个整体,则成中心对称图形.
-21272573025例题解析
例题解析
下列图案都是由字母“”经过变形、组合而成的.其中不是中心对称图形的是
( ).
A B C D
【难度】★
【答案】
【解析】根据中心对称图形的概念可知,均是中心对称图形.
【总结】本题考查了中心对称图形的定义.
在下列四个汽车标志图案中,是中心对称图形的是( )
A B C D
【难度】★
【答案】
【解析】根据中心对称图形的概念可知,中心对称图形是图形沿对称中心旋转后与原 图重合,故选.
【总结】本题考查了中心对称图形的定义.
关于中心对称的两个图形所有对应点的连线________交于一点.
(填“一定”、“不一定”)
【难度】★
【答案】一定.
【解析】关于中心对称的两个图形,对应点的连线必过对应中心.
【总结】本题考查了中心对称的性质.
请写出两个是中心对称图形的汉字_________.
【难度】★
【答案】日、田等.
【解析】中心对称图形是图形沿对称中心旋转后与原图重合.
【总结】本题考查了中心对称的应用.
如图所示的图形是由三个半圆组成的图形,点O是大半圆的圆心,且AC = CD =DB, 则此图关于点O成中心对称的图形是( ?????)
A B C D
【难度】★★
【答案】
【解析】可以把原图形绕着点旋转,刚好与答案的图形重合.
【总结】本题考查了中心对称的定义.
(1)线段;(2)两条相交直线;(3)角;(4)等腰三角形;(5)等边三角形;(6) 平行四边形;(7)矩形;(8)菱形;(9)正方形;(10)圆;(11)等腰梯形等图形中是 中心对称图形的是______________________.(填序号)
【难度】★★
【答案】(1),(6),(7),(8),(9),(10)
【解析】常见中心对称图形:矩形、菱形、正方形、平行四边形、圆、线段、正偶边形等.
【总结】本题考查了常见中心对称图形,注意直线不是轴对称图形.
若两个图形关于某点成中心对称,则下列说法中,正确的有( )个.
对应线段相等;②对应角相等;③周长相等;④面积相等.
A.1 B.2 C.3 D.4
【难度】★★
【答案】
【解析】中心对称的性质:对应角相等、对应线段相等、两个图形全等.
【总结】本题考查了中心对称的性质.
请画出△ABC关于点O成中心对称的对称图形.
【难度】★★
【答案】见解析
【解析】依次连结,并延长到,使得
,连结即为所求图形.
所以为所求.
【总结】本题考查了作中心对称图形,注意找关键点.
10561320238125
请把图中的中心对称图形补画完整.
【难度】★★
【答案】见解析.
【解析】
【总结】本题考查了利用中心对称图形的性质进行画图.
?如图,由16个相同的小正方形拼成的正方形网格,现将其中的两个小正方形涂黑 (如图).请你在下图中再将两个空白的小正方形涂黑,使它成为中心对称图形.
133350016637000【难度】★★
【答案】见解析
【解析】
【总结】本题考查了学生对中心对称图形的概念理解.
330200022479000如图,两个图形关于某点中心对称,看谁能用最简单的方法找出对称中心.你的根 据是什么?
【难度】★★
【答案】见解析.
【解析】找对称中心就是连接两组对应点的连线的交点;
对应点的连线都经过对称中心,并且被对称中心平分.
所以点为所求.
【总结】本题考查了中心对称的性质.
请你用剪刀剪去等边三角形三个角,使余下的部分成为一个中心对称图形,应该怎 样剪?
【难度】★★★
【答案】见解析.
【解析】如图所示正六边形为中心对称图形.(做等边三角形的三等分点即可)
【总结】本题考查了中心对称图形的知识.
如图:已知矩形ABCD的两边AB = 4厘米,BC =12厘米
(1)在图1中画出矩形ABCD的对称中心.(不写结论)
(2)动点P从点A出发,以每秒2厘米的速度沿AD边向点D移动,动点Q同时从点B 出发,以每秒1厘米的速度沿BC边向点C移动 ,联结PQ得图2 .
问:①当P、Q出发几秒后,梯形ABQP的面积是梯形PQCD面积的两倍;
127635019939000当P、Q出发几秒后,图2是一个中心对称图形.
【难度】★★★
【答案】见解析.
【解析】(1)如图1;
(2)解:设运行的时间为秒钟,则,.
①,
,化简得:,解得:.
当出发秒钟后,梯形的面积是梯形面积的两倍.
②由题意得, ,即.
当出发秒后,图2是一个中心对称图形.
【总结】本题考查了中心对称图形的应用.
-922020172720模块二:轴对称
模块二:轴对称
-198120121285知识精讲
知识精讲
1、翻折与轴对称图形
(1)把一个图形沿一条直线翻折过来,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,两个图形中的对应点叫做关于这条直线的对称点.
(2)轴对称图形是一个图形关于某直线对称;轴对称是两个图形关于某条直线对称.
2、轴对称
(1)轴对称:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么称这两个图形关于这条直线对称,也称这两个图形成轴对称.
(2)轴对称的图形的性质:两个图形关于一条直线成轴对称,这两个图形对应线段的长度和对应角的大小相等,它们的形状相同,大小不变;在成轴对称的两个图形中,分别连接两对对应点,取中点,连接两个中点所得的直线就是对称轴.
-20002593345例题解析
例题解析
下列几何图形中,①线段;②角;③圆;④等腰三角形;⑤直角三角形;其中是轴 对称图形的有( )
A.1个 B.2个 C.3个 D.4个
【难度】★
【答案】
【解析】把一个图形沿一条直线翻折过来,直线两旁的部分能够互相重合,这个图形叫做轴 对称图形.
【总结】本题考查了常见的轴对称图形.
下列图形中对称轴最多的是( )
A.圆 B.正方形 C.等腰三角形 D.线段
【难度】★
【答案】
【解析】圆有无数条对称轴;正方形有4条对称轴;等腰三角形有1条对称轴;线段有2 条对称轴.
【总结】本题考查了轴对称图形的对称轴.
下列图案中是轴对称图形的是( )
2008年北京 2004年雅典 1988年汉城 1980年莫斯科
2008年北京 2004年雅典 1988年汉城 1980年莫斯科
A B C D
【难度】★
【答案】
【解析】把一个图形沿一条直线翻折过来,直线两旁的部分能够互相重合,这个图形叫做轴 对称图形.
【总结】本题考查了对生活中的轴对称图形的辨识.
作出下图所示的图形的对称轴:
1238250969010
【难度】★
【答案】见解析.
【解析】
【总结】本题考查了对称轴的画法.
正六边形是轴对称图形,它有 条对称轴.
【难度】★
【答案】
【解析】正六边形有6条对称轴,分别是3条对角线所在直线及3组对边的垂直平分线.
【总结】本题考查了轴对称图形的对称轴的个数.
在下列四种图形变换中,本题图案不包含的变换是( )
中心对称;②旋转;③轴对称; ④平移 .
A.①② B.②③ C.③④ D.①④
226695013970000
【难度】★★
【答案】
【解析】图形的方向发生了改变,不符合平移;绕定点旋转后,图形不能与自身重合, 故不含中心对称.
【总结】本题考查了中心对称、旋转、轴对称、平移的特点.
107950502920将一圆形纸片对折后再对折,得到图3-1中图3,然后沿着图中的虚线剪开,得到 两部分,其中一部分展开后的平面图形是(???? )?? ?
?
A B C D
【难度】★★
【答案】C
【解析】根据题意知,剪去的纸片一定是一个四边形,且对角线相互垂直,故选C.
【总结】本题考查了图形的变换,注意减掉的图形的特征.
3905250259080如图,和关于直线对称,且,,求的度 数和的长.
【难度】★★
【答案】.
【解析】如果两个图形关于某一直线成轴对称,则它们的对应线段
相等,对应角相等.所以.
【总结】本题考查了轴对称图形的性质.
280035022987000尺规:把右图(实线部分)补成以虚线为对称轴的轴对称图形,你会得到一只美 丽蝴蝶的图案(不用写作法、保留作图痕迹).
【难度】★★
【答案】见解析
【解析】
【总结】本题考查了利用轴对称设计图案.
如图,阴影部分是由5个小正方形组成的一个直角图形,请用两种方法分别在下图方格内添涂黑二个小正方形,使它们组成轴对称图形.(试用两种方法)
【难度】★★
【答案】见解析
【解析】
【总结】本题考查了利用轴对称设计图案
如图,等边的边长为a,、分别是、上的点,将沿 直线折叠,点落在点处,且点在外部,则阴影部分图形的周长为
3987800102870 ________________ .
【难度】★★
【答案】.
【解析】等边的边长为,,
沿直线折叠,点落在点处,
,
阴影部分的周长为
.
【总结】本题考查了简单图形的折叠问题.
如图,在公路的同旁有两个仓库、,现需要建一货物中转站,要求到、 两仓库的距离和最短,这个中转站应建在公路旁的哪个位置比较合理?
378460055880【难度】★★★
【答案】见解析
【解析】
作点关于直线的对称点,连接,交直线于点,点为所求.
【总结】本题考查了轴对称图形在实际问题中的应用.
317500048895000打台球问题,在一个长方形球台ABCD上,点P、点Q各放着一个球,现在要求 点P的球先碰AB边,反弹BC边,最后反弹碰到Q的球.问点P的球应该撞击AB的哪 一点,才能够达到上述要求?
【难度】★★★
【答案】见解析.
【解析】在边的另一侧作出点的对称点,
在的另一侧作出的对称点,
连接,所得直线与的交点F,即为点的球应该撞击的位置.
【总结】本题考查了图形的对称问题,综合性较强,注意认真分析.
2686050121793000地面上有不共线的三点A、B、C,一只青蛙位于异于A、B、C的点P.第一步, 青蛙从P点跳到关于A的对称点;第二步,青蛙从跳到关于B的对称点;第三 步,青蛙从跳到关于C的对称点;第四步,从跳到关于A的对称点;…,如 此不断地跳下去,问青蛙跳完6666步后落在什么位置上?
【难度】★★★
【答案】见解析
【解析】由图可知:,
两对角相等,平行且等于,
如果有,则同样可得平行且等于,平行且等于,
构成一个三角形,同理也构成一个三角形,两个三角形中两个边分别平行 且相等,可证明另一边平行且相等,这样就可以证明与重合,即就是, 则每6步是一个轮回,故6666步落于点.
【总结】本题考查了图形的对称规律,注意认真分析.
-1743075113665随堂检测
随堂检测
下列“表情”中属于轴对称图形的是( )
A B C D
【难度】★
【答案】
【解析】把一个图形沿一条直线翻折过来,直线两旁的部分能够互相重合,这个图形叫做轴 对称图形.
【总结】本题主要考查了简单的轴对称图形的判断.
下列交通标志中,不是轴对称图形的是( )
A B C D
【难度】★
【答案】
【解析】把一个图形沿一条直线翻折过来,直线两旁的部分能够互相重合,这个图形叫做轴 对称图形.
【总结】本题考查了简单的轴对称图形.
下列图形中,是中心对称图形的是( )
A B C D
【难度】★
【答案】
【解析】根据中心对称图形的概念可知,中心对称图形是图形沿对称中心旋转后与原 图重合.
【总结】本题考查了中心对称图形的概念.
正2n边形,有______条对称轴,它有________个对称中心.
【难度】★
【答案】;1.
【总结】本题考查了轴对称图形的定义及对称轴的条数.
下列图案中,既是轴对称图形,又是中心对称图形的是(?? )
A B C D
【难度】★★
【答案】
【解析】把一个图形沿一条直线翻折过来,直线两旁的部分能够互相重合,这个图形叫做轴 对称图形;中心对称图形是图形沿对称中心旋转后与原图重合.
【总结】本题考查了轴对称图形和中心对称图形的定义.
下列图案中,有且只有三条对称轴的是( )
A B C D
【难度】★★
【答案】
【解析】有两条对称轴;有四条对称轴;不是轴对称图形.
【总结】本题考查了轴对称图形的对称轴的条数.
1972945420370下面四个图形中,从几何图形的性质考虑,哪一个与其他三个不同?请指出这个 图形,并简述你的理由.
答:图形_______________;
理由是________________.
【难度】★★
【答案】②;只有②不是轴对称图形.
【解析】四个图形中,只有②不是轴对称图形,其余都是.
【总结】本题考查了几何图形的变换性质.
下列图形中,既是轴对称图形又是中心对称图形的是( )
A.等腰三角形 B.等腰梯形 C.正方形 D.平行四边形
【难度】★★
【答案】
【解析】是轴对称图形,但不是中心对称图形;是轴对称图形,但不是中心对称图形;
不是轴对称图形,但是中心对称图形.
【总结】本题考查了轴对称图形和中心对称图形的定义.
下列说法中错误的是( ).
A.圆有无数条对称轴,一个对称中心
B.等边三角形有三条对称轴,三个对称中心
C.正方形有四条对称轴,一个对称中心
D.等腰梯形仅有一条对称轴,没有对称中心
【难度】★★
【答案】
【解析】所有中心对称图形都只有一个对称中心;故错误.
【总结】本题考查了常见的轴对称图形特点.
349885021590000作出下图所示的成轴对称图形的对称轴:
1644650120650【难度】★★
【答案】
【解析】
【总结】本题考查了成轴对称图形对称轴的画法,主要是找出关键点.
如图,画出半圆A关于点F中心对称的图形.
2705100163830【难度】★★
【答案】见解析
【解析】
作半圆的直径的两外端点点关于点对称点,再画半圆.
【总结】本题考查了中心对称图形的画法.
2355850425450如图(1)(2)所示的两组长方形能否关于某一点成中心对称?若能,则请画出 其对称中心.
【难度】★★
【答案】见解析
222250015748000【解析】(1)能成中心对称;(2)不能.
如图(1)点为所求.
【总结】本题考查了中心对称的两个图形,对称中心的画法.
如图是由3个同样的小正方形所组成,请再补上一个同样的小正方形,使得由4 个小正方形组成的图形成为一个中心对称图形.要求:画出所有的情况,并且在所添画 的正方形中用数字标出.
【难度】★★★
【答案】见解析
【解析】共有三种情况.
【总结】本题考查了中心对称图形的定义.
如图跳棋盘,其中格点上的黑色点为棋子,剩余的格点上没有棋子.我们约定跳棋游戏的规则是:把跳棋棋子在棋盘内沿直线隔着棋子对称跳行,跳行一次称为一步.已
4044950228600知点为已方一枚棋子,欲将棋子跳进对方区域(阴影部分的格点),则跳行的最
少步数为(??? )
?????? A.2步????????????????? B.3步???????????????????C.4步????????????????? D.5步
【难度】★★★
【答案】
【解析】
【总结】本题考查了‘桌球问题’中的轴反射.
如图,,角内有点,且OP = 2,在角的两边有两点、(均不
3577590158750 同于点), 求作、,使得的周长的最小,并求出最小值.
【难度】★★★
71942027305000【答案】.
【解析】如图:
分别作关于的对称点,连接交于,则 符合条件,连接,则,的周长,
则,所以为等腰直角三角形,
.
【总结】本题考查了轴对称图形的性质及勾股定理的应用,综合性较强,注意认真分析.
-10604581280课后作业
课后作业
下面四个标志图是中心对称图形的是( )
476250163830A
B
C
D
A
B
C
D
【难度】★
【答案】
【解析】生活中的中心对称图形,参考中心对称图形定义.
【总结】本题考查了中心对称图形的定义.
正八边形________中心对称图形.(填“是”或“不是”).
【难度】★
【答案】是
【解析】因为将正八边形绕正八边形的中心旋转后能够与自身重合,所以为中心对称 图形.
【总结】本题考查了中心对称图形的定义.
圆______是中心对称图形,两个圆__________关于某点成中心对称.(填“一定”、 “不一定”或“一定不”)
【难度】★
【答案】一定;不一定.
【解析】圆是中心对称图形,因为不确定两个圆的大小,所以两个圆不一定关于某点成中心 对称.
【总结】本题考查了圆这个基本图形的中心对称性.
下列图形中,既是轴对称图形,又是中心对称图形的是( )
【难度】★
【答案】
【解析】是轴对称图形,但不是中心对称图形;是轴对称图形,但不是中心对称图形;
不是轴对称图形,但是中心对称图形.
【总结】本题考查了轴对称图形和中心对称图形的定义.
3571875336550如图,直线是四边形的对称轴,若,有下面的结论:①; ②; ③; ④,其中正确的结论有_______.
【难度】★★
【答案】①②③.
【解析】解:轴对称图形的两部分是全等的,所以①②③正确.
【总结】本题考查了轴对称图形的性质.
如图所示,将一张正方形纸片对折两次,然后在上面打个洞,则纸片展开后 是 .
(1) (2) (3) (4)
【难度】★★
【答案】
【解析】当正方形纸片两次沿对角线对折成为一直角三角形时,在平行于斜边的位置打3 个洞,则直角顶点处完好,则原正方形中间无损,且有12个洞.
【总结】本题考查了空间思维及折叠处理实际问题.
下图中②③④⑤分别由①图顺时针旋转180°变换而成的是____________.
?
① ② ③ ④ ⑤
【难度】★★
【答案】④.
【解析】根据中心对称图形的概念可知,中心对称图形是图形沿对称中心旋转后与原 图重合.
【总结】本题考查了中心对称图形的定义.
某校计划建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到的设
计方案有等边三角形、等腰梯形、菱形、正五边形等四种方案,你认为符合条件的是(??? )
???? A. 等边三角形??? ??? B.等腰梯形?? ???C.菱形????????? D. 正五边形
【难度】★★
【答案】.
【解析】等边三角形是轴对称图形,但不是中心对称图形;等腰梯形是轴对称图形,但不是 中心对称图形;正五边形是轴对称图形,但不是中心对称图形.
【总结】本题考查了基本图形的特性.
3365500654050两个完全一样的三角形,可以拼出各种不同的图形,如图已画出其中一个三角形, 请你分别补画出另一个与其一模一样的三角形,使每个图形分别构成不同的中心对称 图形(所画三角形可与原三角形有重叠部分).
?【难度】★★
【答案】
180213015240000【解析】
330835023241000
370205021590000172085018478500-2413008255000
【总结】本题考查了中心对称图形的定义及画图.
在由小正方形组成的形的图中,用三种不同方法添画一个小正方形,使它成为 轴对称图形.
方法一 方法二 方法三
【难度】★★★
【答案】见解析
【解析】
【总结】本题考查了轴对称图形的性质.
菱形ABCD的两条对角线AC、BD互相垂直平分,相交于点O,O就是它的对 称中心,过它的顶点A、D向BC及其延长线作垂线AE、DF,E、F为垂足,图中的三 角形可以看作
(1)由平移变换得到的有_________对,它们是__________;
309499031750 (2)由旋转变换得到的有_________对,它们是__________;
(3)由翻折变换得到的有_________对,它们是__________.
【难度】★★★
【答案】见解析
【解析】(1)由平移变换得到的有对,为;
(2)由旋转变换得到的有对,
为、、
、;
(3)由翻折变换得到的有对,为
.
【总结】本题考查了图形的几种变换,注意每种变换的特征.
已知:、两点在直线的同侧,在上求作一点,使得最大.
34544006985【难度】★★★
【答案】见解析
【解析】
连接与的交点即为,根据三角形两边之差小于第三边.
【总结】本题考查了图形最值问题的实际操作问题.
两个人轮流在一张圆心桌面上摆放硬币,规则是每人每次摆一枚,硬币不能互相 重叠,也不能有一部分在桌面的边缘之外,摆好之后不许再移动,这样经过多次摆放, 直到谁最先摆不下硬币谁就认输,按照这个规则,你用什么方法才能保证取胜?
【难度】★★★
【答案】争取先放,并且把第1枚硬币放在桌面的对称中心上.
【解析】你要争取先放,并且把第1枚硬币放在桌面的对称中心上,以后你应该根据对方所
放硬币的位置,在它关于中心对称的位置上放下一枚同样大小的下一枚硬币,你就能保
证在其对称位置上放下一枚同样大小的硬币,即可.
【总结】本题考查了中心对称的性质运用.
