沪教版七年级上册数学秋季班第19讲:期末复习(一)教师版
文档属性
| 名称 | 沪教版七年级上册数学秋季班第19讲:期末复习(一)教师版 |
|
|
| 格式 | docx | ||
| 文件大小 | 1002.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-21 00:00:00 | ||
图片预览





文档简介
-4159258890期末复习(一)
期末复习(一)
-257175151130内容分析
内容分析
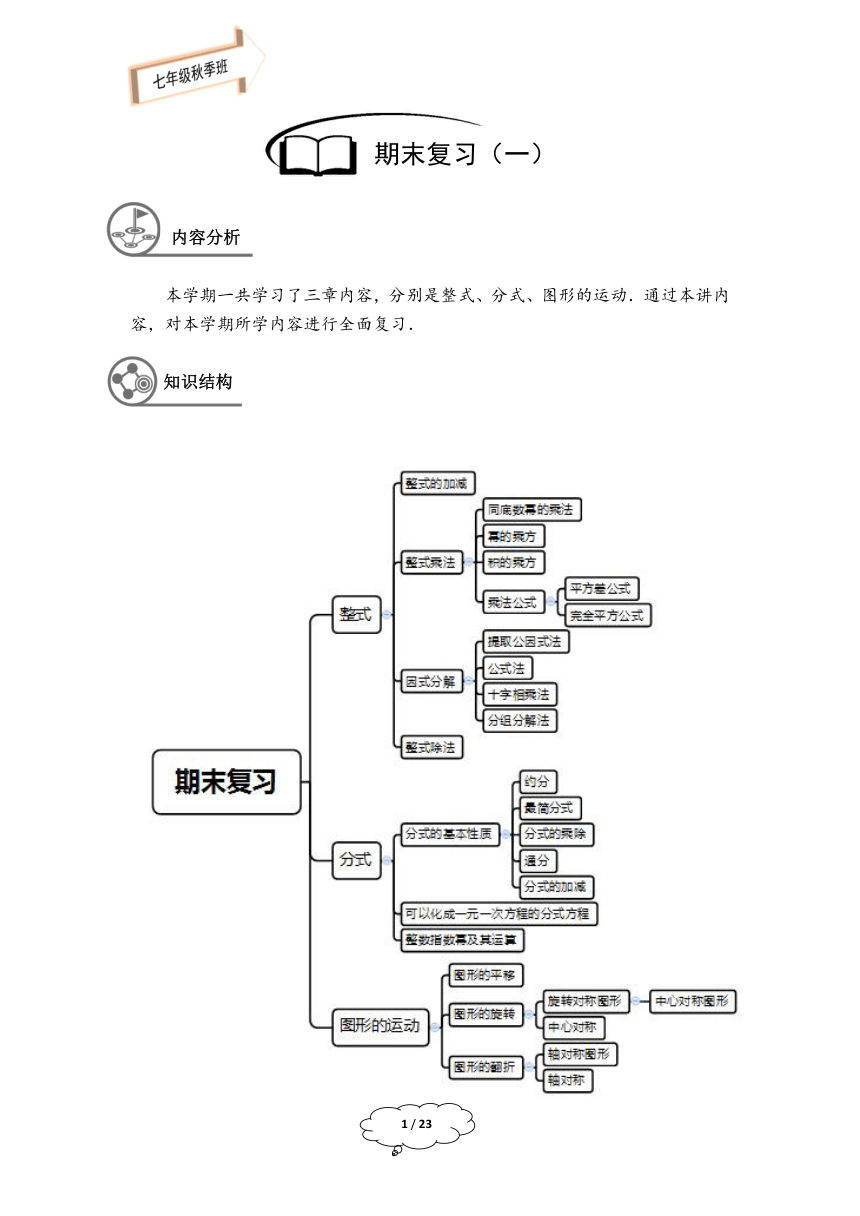
本学期一共学习了三章内容,分别是整式、分式、图形的运动.通过本讲内容,对本学期所学内容进行全面复习.
-29527592710 知识结构
知识结构
-317506350选择题
选择题
下列各式中,与是同类项的是( ).
. . . .
【难度】★
【答案】B
【解析】同类项是指(1)所含字母相同;(2)相同字母的指数相同.
【总结】本题考查了同类项的定义.
如果分式有意义,那么应满足的条件是( ).
. . . .
【难度】★
【答案】B
【解析】分式有意义指的是分母,即.
【总结】本题考查了分式有意义的条件.
若,则等于( ).
. . . .
【难度】★
【答案】C
【解析】.
【总结】本题考查了完全平方公式的公式变形.
下列图形中是旋转对称图形但不是中心对称图形的是( ).
111125247653679825121920
【难度】★
【答案】A
【解析】中心对称图形是指把一个图形绕一点旋转180度后能与自身重合;旋转对称图形是
指把一个图形绕一定点旋转一定角度(小于周角)后能与自身重合.
【总结】本题考查了旋转对称图形和中心对称图形的概念.
下列等式中,从左到右的变形是因式分解的是( ).
. .
. .
【难度】★
【答案】D
【解析】因式分解是指把一个多项式化为几个整式的乘积的形式.
【总结】本题考查了因式分解的概念.
的计算结果是( )
. . . .
【难度】★★
【答案】C
【解析】,同底数幂相除,底数不变,指数相减.
【总结】本题考查了幂的乘方及同底数幂相除运算.
下列格式中,等式成立的是( ).
. .
. .
【难度】★★
【答案】A
【解析】A中正确.
【总结】本题考查了分式的基本性质的运用.
如果将分式中的和都扩大到原来的倍,那么分式的值( ).
.扩大到原来的倍 .扩大到原来的倍
.缩小到原来的 .不变
【难度】★★
【答案】A
【解析】和都扩大到原来的倍,即为和;
则,
所以原分式的值扩大到原来的3倍.
【总结】本题考查了分式的基本性质的运用.
小敏和小明练习打字,小敏比小明每分钟多打个字,完成字文稿小敏比 小明少用分钟,设小明每分钟打个字,则可列方程( ).
. .
. .
【难度】★★
【答案】A
【解析】解:设小明每分钟打个字,则小敏每分钟打个字,
由题意得:,故选A.
【总结】本题考查了列分式方程解应用题.
二次三项式分解因式的结果如下:①;
②;③;④.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
【难度】★★
【答案】C
【解析】①错;②③④正确.
【总结】本题考查了因式分解的十字相乘法.
如果能被整除,则可取( )
A.1、2、3 B.任何整数 C.不小于3的整数 D.大于3的整数
【难度】★★★
【答案】C
【解析】解:;则,.
【总结】本题考查了数的整除及同底数幂的除法.
若为实数,则使分式有意义的是( ).
. .不同时为零
. .但均不为
【难度】★★★
【答案】B
【解析】使分式有意义,则分母,即就是不同时为零.
【总结】本题考查了分式有意义的条件.
34486851143635如图,一长为,宽为的长方形木板(其中),在桌面上作无滑
动的顺时针方向的翻滚,木板上的点位置变化为,其中第二次翻滚时被
桌面上一小木块挡住,使木板和桌面成角,则点翻滚到位置时共走过路径长
为( ).
. .
. .
【难度】★★★
【答案】C
【解析】解:点以点为旋转中心,以为旋转角,顺时针旋转得到;同理是 由以点为旋转中心,以为旋转角,顺时针旋转得到.
34163005715000
点翻滚到位置时共走过路径长为:
.
【总结】本题考查了旋转的性质及弧长公式的运用.
-8890026670填空题
填空题
将按字母x降幂排列_______________.
【难度】★
【答案】.
【解析】①看清那一个字母;②看清升降幂.
【总结】本题考查了按某以字母的降幂排列.
实验证明:钢轨温度每变化,每一米钢轨就伸缩米,如果一个月
中气温上下相差,那么对于米长的铁路, 最长可伸长_______________米.(用
科学记数法表示)
【难度】★
【答案】.
【解析】解:(米);
绝对值小于1的正数也可以利用科学计数法表示,一般形式为.
【总结】本题考查了科学计数法负整数指数幂的表示.
在线段、角、正三角形、长方形、正方形、等腰梯形和圆中,共有 个为旋
转对称图形.
【难度】★
【答案】5
【解析】其中线段、正三角形、长方形、正方形、圆是旋转对称图形.
【总结】本题考查了常见的旋转对称图形.
当___________时,方程的值为零.
【难度】★★
【答案】-3.
【解析】当分子,即时;当代入分母,分式无意义;
当代入分母,分式值为0.所以时,原分式方程值为零.
【总结】本题考查了分式值为零的条件.
计算:_______________.
【难度】★★
【答案】.
【解析】.
【总结】本题考查了分式的乘除运算及分式的化简.
当________时,方程会产生增根.
【难度】★★
【答案】1
【解析】由题意得方程的增根是,即;
方程两边同时乘以,得,即.
将代入,得,
所以,当时,原方程有增根.
【总结】本题考查了分式方程产生增根的条件及对方程的增根的理解.
因式分解:(1)_______________;
(2)=________________;
(3)________________.
【难度】★
【答案】见解析.
【解析】(1);
(2);
(3)
.
【总结】本题考查了因式分解的方法与技巧.
3511550234950如图,个大小一样的正三角形拼在一起,将绕着点旋转与重合,
那么最小旋转角度为_________.
【难度】★★
【答案】.
【解析】与重合,即点落在点上,
点落在点上,即至少旋转了.
【总结】本题考查了旋转的性质及旋转角的大小判定.
3619500222250如图,是正三角形内的一点,将三角形绕点顺时针方向旋转能与
三角形重合,则.
【难度】★★
【答案】.
【解析】由旋转角都相等可知,.
【总结】本题考查了旋转的性质和运用.
若,则代数式的值是________.
【难度】★★
【答案】-3.
【解析】;又由,所以原式;
,故原式的值为-3.
【总结】本题考查了因式分解的技巧及整体代入求值的思想.
2673279-58420小杰从镜子中看到电子钟的示数是 ,那么此时实际时间是
____________.
【难度】★★
【答案】21:05.
【解析】镜子中看到的数字与实际数字是关于镜面垂直的线对称.
【总结】本题考查了镜面对称问题.
若关于的方程的解为正数,则的取值范围是_________.
【难度】★★
【答案】
【解析】解:原方程整理得:,则;
原方程有解,,即,故,
又方程的解为正数,,故;
所以.
【总结】本题考查了分式方程的解及分式方程有意义的综合运用.
如果关于的多项式是完全平方式,那么.
【难度】★★★
【答案】.
【解析】分三种情况:①当和都为平方项时,; ②当为中间项时,;
③当为中间项时,,此时代数式不是多项式,故不满足.
【总结】本题考查了完全平方公式的应用.
若,则用的代数式来表示=________.
【难度】★★★
【答案】.
【解析】.
【总结】本题考查了幂的乘方及积的乘方的运用.
已知,则.
【难度】★★★
【答案】169.
【解析】.
【总结】本题考查了同底数幂运算及乘法分配率的综合运用.
下图是某同学在沙滩上涌石子摆成的“小房子”
2444750227330
观察图形的变化规律,写出第个小房子用了__________块石子.
【难度】★★★
【答案】.
【解析】解:该小房子用的石子数可以分两部分找规律:
屋顶:第一个是1,第二个是3,第三个是5,...以此类推,第个是;
下边:第一个是4,第二个是9,第三个是16,...以此类推,第个是.
所以共有.
【总结】本题考查了用字母表示数观察规律题.
-1587562230解答题
解答题
化简:.
【难度】★
【答案】.
【解析】.
【总结】本题考查了积的乘方及同底数幂的运算.
因式分解:.
【难度】★
【答案】.
【解析】.
【总结】本题考查了因式分解中分组分解法.
小明今年岁,小明的妈妈今年岁.几年后小明的年龄是他妈妈年龄的?
【难度】★
【答案】.
【解析】解:设年后小明年龄是他妈妈年龄的,
由题意得:
解得:
所以年后小明年龄是他妈妈年龄的.
【总结】本题考查了利用列方程解决实际问题.
先化简,后求值:,其中.
【难度】★
【答案】.
【解析】
.
当时,原式.
【总结】本题考查了分式的化简求值问题,注意要先化简后求值.
计算:.
【难度】★
【答案】.
【解析】.
【总结】本题考查了分式的加减运算,要注意先通分再计算.
解方程:
(1); (2).
【难度】★
【答案】(1);(2).
【解析】解:(1)分式两边同乘,得,化简得:,
解得:.经检验:是原分式方程的解,
所以是原分式方程的解;
(2)方程两边同乘,得:
解得:,经检验:是原分式方程的解,
所以原分式方程的解是.
【总结】本题考查了分式方程的解法步骤,注意要检验根.
已知,(1)求的值;(2)求的值.
【难度】★★
【答案】(1)11;(2)13.
【解析】(1);
(2).
【总结】本题考查了完全平方公式的变形及计算.
计算:.
【难度】★★
【答案】
【解析】.
【总结】本题考查了负指数幂及分式的加减运算.
已知为自然数,且,求的值.
【难度】★★
【答案】.
【解析】, .
【总结】本题考查了幂的乘方及积的乘方法则的综合运用.
已知,,、是正整数且.
求下列各式的值:①;②.
【难度】★★
【答案】①;②.
【解析】解:①;②.
【总结】本题考查了同底数幂运算法则的运用.
比较的大小.
【难度】★★
【答案】.
【解析】解:;;
;
; .
【总结】本题考查了负整数指数幂的大小比较.
已知:,把化简后求值.
【难度】★★
【答案】.
【解析】解:,
由已知得:,即;则原式.
【总结】本题考查了分式的运算及代数求值.
已知两个分式:=,=,其中且.下面有三个
结论:①=;②、互为倒数;③、互为相反数.请问哪个结论正确?
为什么?
【难度】★★
【答案】③.
【解析】解:,;
,即、互为相反数.
【总结】本题考查了分式的化简及运算.
已知,求的值.
【难度】★★
【答案】
【解析】解:原式
,
当时,原式.
【总结】本题考查了分式的混合运算及整体代入求值的思想运用.
已知,求的值.
【难度】★★
【答案】.
【解析】解:原式,
,,即,
原式.
【总结】本题考查了分式化简运算及代入求值的思想运用.
某班部分同学同学准备新年期间去博物馆参观,按原预定人数估计,共需费用
元,后因人数增加到原来的倍,可享受优惠,只需元,而参加的每位同学所分摊的费用比原来估计所需费用少元,原来预定人数是多少?
【难度】★★
【答案】15人.
【解析】解:设原来预定人数为人,
则,
解得: .
经检验:为原分式方程的解.
所以原来预定人数为人.
【总结】本题考查了列分式方程解应用题,注意要进行检验.
已知,,,求的值.
【难度】★★
【答案】.
【解析】将看作已知数,求出和,代入原式计算,
由得到,
,解得:,
则原式.
【总结】本题考查了分式方程的化简求值.
(1)如图所示的两个图形成中心对称,你能找到对称中心吗?
342900167640
(2)先将方格纸中的图形向右平移3格,然后再向下平移2格.
327787047625
【难度】★★
【答案】
【解析】(1)
所以点为所求.
41275010541000
(2)
【总结】本题考查了中心对称及图形的平移.
235585015621000画出三角形关于直线的轴对称的三角形.
【难度】★★
【答案】见解析
【解析】
如图为所求.
【总结】本题考查了成轴对称图形的画法.
图是用两个如图所示的直角三角形拼得的新图形,其中是中心对称
图形的是______________;是轴对称的图形是______________.
3524250107950
1162050196850
190500191770
20789906350
(A) (B) (C) (D)
【难度】★★
【答案】;.
【解析】中心对称图形是指把一个图形绕一点旋转180度后能与自身重合;轴对称图形是
在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形.
【总结】本题考查了中心对称图形及轴对称图形的概念.
分解因式:.
【难度】★★★
【答案】
【解析】
【总结】本题考查了因式分解的整体换元思想,注意分解要彻底.
已知多项式,求此多项式取最小值时的值,并求出
此最小值.
【难度】★★★
【答案】;此时最小值为.
【解析】
,且 ,
,原多项式的最小值为,此时.
【总结】本题考查了完全平方公式的运用,注意配方思想的运用.
解方程:.
【难度】★★★
【答案】.
【解析】解:,即,所以,
所以 ,解得:.
【总结】本题考查了同底数幂的运用.
已知,求代数式的值.
【难度】★★★
【答案】.
【解析】解:由,得:,
所以原式.
【总结】本题考查了等式的变形及整体代入求值的运用.
试判断的值与的大小关系,并证明你的结论.
【难度】★★★
【答案】见解析.
【解析】解:
;
所以.
【总结】本题考查了作差法比较大小及平方差公式的运用.
阅读下列材料:
(1)用作差可以比较两数的大小,即:若,则;
(2)平方式具有非负性,即.
请根据材料信息,比较,的大小.
【难度】★★★
【答案】.
【解析】解:
;
∵, ,即;
,即.
【总结】本题考查了利用作差法比较两数的大小以及配完全平方的运用.
如图,将六个正方形无缝拼接在一起构成一个长方形,其中最小的一个正方形边
长为,求拼成的长方形面积.
349250054610【难度】★★★
【答案】.
【解析】解:设右下角两个相等的小正方形边长为.
由题意得:
解得:
即长方形长为,宽为,
所以面积为.
【总结】 本题考查了字母表示数的应用.
用四块如图1所示正方形瓷砖拼成一个新的正方形,请你在图2、图3、图4中各画一种拼法.要求:其中一个图形既是轴对称图形,又是中心对称图形;一个图形是轴对称图形,但不是中心对称图形;一个图形是中心对称图形,但不是轴对称图形.
0175260377190017526025146001752601257300175260
342900175260342900175260
34290045720图1
图1
148590076200图2
图2
400050076200图4
图4
274320076200图3
图3
【难度】★★
【答案】见解析
【解析】
【总结】本题考查了中心对称图形及轴对称图形的性质.
如图,在上找到、两点,且,在的左边,使四边形
3472180120650的周长最短.
【难度】★★★
【答案】见解析
【解析】过点作关于直线的对称点,过点作
,使得,连接交直线于
在直线上截取,则四边形的周长最短.
【总结】本题考查了点的对称及两点之间线段最短的应用.
期末复习(一)
-257175151130内容分析
内容分析
本学期一共学习了三章内容,分别是整式、分式、图形的运动.通过本讲内容,对本学期所学内容进行全面复习.
-29527592710 知识结构
知识结构
-317506350选择题
选择题
下列各式中,与是同类项的是( ).
. . . .
【难度】★
【答案】B
【解析】同类项是指(1)所含字母相同;(2)相同字母的指数相同.
【总结】本题考查了同类项的定义.
如果分式有意义,那么应满足的条件是( ).
. . . .
【难度】★
【答案】B
【解析】分式有意义指的是分母,即.
【总结】本题考查了分式有意义的条件.
若,则等于( ).
. . . .
【难度】★
【答案】C
【解析】.
【总结】本题考查了完全平方公式的公式变形.
下列图形中是旋转对称图形但不是中心对称图形的是( ).
111125247653679825121920
【难度】★
【答案】A
【解析】中心对称图形是指把一个图形绕一点旋转180度后能与自身重合;旋转对称图形是
指把一个图形绕一定点旋转一定角度(小于周角)后能与自身重合.
【总结】本题考查了旋转对称图形和中心对称图形的概念.
下列等式中,从左到右的变形是因式分解的是( ).
. .
. .
【难度】★
【答案】D
【解析】因式分解是指把一个多项式化为几个整式的乘积的形式.
【总结】本题考查了因式分解的概念.
的计算结果是( )
. . . .
【难度】★★
【答案】C
【解析】,同底数幂相除,底数不变,指数相减.
【总结】本题考查了幂的乘方及同底数幂相除运算.
下列格式中,等式成立的是( ).
. .
. .
【难度】★★
【答案】A
【解析】A中正确.
【总结】本题考查了分式的基本性质的运用.
如果将分式中的和都扩大到原来的倍,那么分式的值( ).
.扩大到原来的倍 .扩大到原来的倍
.缩小到原来的 .不变
【难度】★★
【答案】A
【解析】和都扩大到原来的倍,即为和;
则,
所以原分式的值扩大到原来的3倍.
【总结】本题考查了分式的基本性质的运用.
小敏和小明练习打字,小敏比小明每分钟多打个字,完成字文稿小敏比 小明少用分钟,设小明每分钟打个字,则可列方程( ).
. .
. .
【难度】★★
【答案】A
【解析】解:设小明每分钟打个字,则小敏每分钟打个字,
由题意得:,故选A.
【总结】本题考查了列分式方程解应用题.
二次三项式分解因式的结果如下:①;
②;③;④.其中正确的个数为( )
A.1个 B.2个 C.3个 D.4个
【难度】★★
【答案】C
【解析】①错;②③④正确.
【总结】本题考查了因式分解的十字相乘法.
如果能被整除,则可取( )
A.1、2、3 B.任何整数 C.不小于3的整数 D.大于3的整数
【难度】★★★
【答案】C
【解析】解:;则,.
【总结】本题考查了数的整除及同底数幂的除法.
若为实数,则使分式有意义的是( ).
. .不同时为零
. .但均不为
【难度】★★★
【答案】B
【解析】使分式有意义,则分母,即就是不同时为零.
【总结】本题考查了分式有意义的条件.
34486851143635如图,一长为,宽为的长方形木板(其中),在桌面上作无滑
动的顺时针方向的翻滚,木板上的点位置变化为,其中第二次翻滚时被
桌面上一小木块挡住,使木板和桌面成角,则点翻滚到位置时共走过路径长
为( ).
. .
. .
【难度】★★★
【答案】C
【解析】解:点以点为旋转中心,以为旋转角,顺时针旋转得到;同理是 由以点为旋转中心,以为旋转角,顺时针旋转得到.
34163005715000
点翻滚到位置时共走过路径长为:
.
【总结】本题考查了旋转的性质及弧长公式的运用.
-8890026670填空题
填空题
将按字母x降幂排列_______________.
【难度】★
【答案】.
【解析】①看清那一个字母;②看清升降幂.
【总结】本题考查了按某以字母的降幂排列.
实验证明:钢轨温度每变化,每一米钢轨就伸缩米,如果一个月
中气温上下相差,那么对于米长的铁路, 最长可伸长_______________米.(用
科学记数法表示)
【难度】★
【答案】.
【解析】解:(米);
绝对值小于1的正数也可以利用科学计数法表示,一般形式为.
【总结】本题考查了科学计数法负整数指数幂的表示.
在线段、角、正三角形、长方形、正方形、等腰梯形和圆中,共有 个为旋
转对称图形.
【难度】★
【答案】5
【解析】其中线段、正三角形、长方形、正方形、圆是旋转对称图形.
【总结】本题考查了常见的旋转对称图形.
当___________时,方程的值为零.
【难度】★★
【答案】-3.
【解析】当分子,即时;当代入分母,分式无意义;
当代入分母,分式值为0.所以时,原分式方程值为零.
【总结】本题考查了分式值为零的条件.
计算:_______________.
【难度】★★
【答案】.
【解析】.
【总结】本题考查了分式的乘除运算及分式的化简.
当________时,方程会产生增根.
【难度】★★
【答案】1
【解析】由题意得方程的增根是,即;
方程两边同时乘以,得,即.
将代入,得,
所以,当时,原方程有增根.
【总结】本题考查了分式方程产生增根的条件及对方程的增根的理解.
因式分解:(1)_______________;
(2)=________________;
(3)________________.
【难度】★
【答案】见解析.
【解析】(1);
(2);
(3)
.
【总结】本题考查了因式分解的方法与技巧.
3511550234950如图,个大小一样的正三角形拼在一起,将绕着点旋转与重合,
那么最小旋转角度为_________.
【难度】★★
【答案】.
【解析】与重合,即点落在点上,
点落在点上,即至少旋转了.
【总结】本题考查了旋转的性质及旋转角的大小判定.
3619500222250如图,是正三角形内的一点,将三角形绕点顺时针方向旋转能与
三角形重合,则.
【难度】★★
【答案】.
【解析】由旋转角都相等可知,.
【总结】本题考查了旋转的性质和运用.
若,则代数式的值是________.
【难度】★★
【答案】-3.
【解析】;又由,所以原式;
,故原式的值为-3.
【总结】本题考查了因式分解的技巧及整体代入求值的思想.
2673279-58420小杰从镜子中看到电子钟的示数是 ,那么此时实际时间是
____________.
【难度】★★
【答案】21:05.
【解析】镜子中看到的数字与实际数字是关于镜面垂直的线对称.
【总结】本题考查了镜面对称问题.
若关于的方程的解为正数,则的取值范围是_________.
【难度】★★
【答案】
【解析】解:原方程整理得:,则;
原方程有解,,即,故,
又方程的解为正数,,故;
所以.
【总结】本题考查了分式方程的解及分式方程有意义的综合运用.
如果关于的多项式是完全平方式,那么.
【难度】★★★
【答案】.
【解析】分三种情况:①当和都为平方项时,; ②当为中间项时,;
③当为中间项时,,此时代数式不是多项式,故不满足.
【总结】本题考查了完全平方公式的应用.
若,则用的代数式来表示=________.
【难度】★★★
【答案】.
【解析】.
【总结】本题考查了幂的乘方及积的乘方的运用.
已知,则.
【难度】★★★
【答案】169.
【解析】.
【总结】本题考查了同底数幂运算及乘法分配率的综合运用.
下图是某同学在沙滩上涌石子摆成的“小房子”
2444750227330
观察图形的变化规律,写出第个小房子用了__________块石子.
【难度】★★★
【答案】.
【解析】解:该小房子用的石子数可以分两部分找规律:
屋顶:第一个是1,第二个是3,第三个是5,...以此类推,第个是;
下边:第一个是4,第二个是9,第三个是16,...以此类推,第个是.
所以共有.
【总结】本题考查了用字母表示数观察规律题.
-1587562230解答题
解答题
化简:.
【难度】★
【答案】.
【解析】.
【总结】本题考查了积的乘方及同底数幂的运算.
因式分解:.
【难度】★
【答案】.
【解析】.
【总结】本题考查了因式分解中分组分解法.
小明今年岁,小明的妈妈今年岁.几年后小明的年龄是他妈妈年龄的?
【难度】★
【答案】.
【解析】解:设年后小明年龄是他妈妈年龄的,
由题意得:
解得:
所以年后小明年龄是他妈妈年龄的.
【总结】本题考查了利用列方程解决实际问题.
先化简,后求值:,其中.
【难度】★
【答案】.
【解析】
.
当时,原式.
【总结】本题考查了分式的化简求值问题,注意要先化简后求值.
计算:.
【难度】★
【答案】.
【解析】.
【总结】本题考查了分式的加减运算,要注意先通分再计算.
解方程:
(1); (2).
【难度】★
【答案】(1);(2).
【解析】解:(1)分式两边同乘,得,化简得:,
解得:.经检验:是原分式方程的解,
所以是原分式方程的解;
(2)方程两边同乘,得:
解得:,经检验:是原分式方程的解,
所以原分式方程的解是.
【总结】本题考查了分式方程的解法步骤,注意要检验根.
已知,(1)求的值;(2)求的值.
【难度】★★
【答案】(1)11;(2)13.
【解析】(1);
(2).
【总结】本题考查了完全平方公式的变形及计算.
计算:.
【难度】★★
【答案】
【解析】.
【总结】本题考查了负指数幂及分式的加减运算.
已知为自然数,且,求的值.
【难度】★★
【答案】.
【解析】, .
【总结】本题考查了幂的乘方及积的乘方法则的综合运用.
已知,,、是正整数且.
求下列各式的值:①;②.
【难度】★★
【答案】①;②.
【解析】解:①;②.
【总结】本题考查了同底数幂运算法则的运用.
比较的大小.
【难度】★★
【答案】.
【解析】解:;;
;
; .
【总结】本题考查了负整数指数幂的大小比较.
已知:,把化简后求值.
【难度】★★
【答案】.
【解析】解:,
由已知得:,即;则原式.
【总结】本题考查了分式的运算及代数求值.
已知两个分式:=,=,其中且.下面有三个
结论:①=;②、互为倒数;③、互为相反数.请问哪个结论正确?
为什么?
【难度】★★
【答案】③.
【解析】解:,;
,即、互为相反数.
【总结】本题考查了分式的化简及运算.
已知,求的值.
【难度】★★
【答案】
【解析】解:原式
,
当时,原式.
【总结】本题考查了分式的混合运算及整体代入求值的思想运用.
已知,求的值.
【难度】★★
【答案】.
【解析】解:原式,
,,即,
原式.
【总结】本题考查了分式化简运算及代入求值的思想运用.
某班部分同学同学准备新年期间去博物馆参观,按原预定人数估计,共需费用
元,后因人数增加到原来的倍,可享受优惠,只需元,而参加的每位同学所分摊的费用比原来估计所需费用少元,原来预定人数是多少?
【难度】★★
【答案】15人.
【解析】解:设原来预定人数为人,
则,
解得: .
经检验:为原分式方程的解.
所以原来预定人数为人.
【总结】本题考查了列分式方程解应用题,注意要进行检验.
已知,,,求的值.
【难度】★★
【答案】.
【解析】将看作已知数,求出和,代入原式计算,
由得到,
,解得:,
则原式.
【总结】本题考查了分式方程的化简求值.
(1)如图所示的两个图形成中心对称,你能找到对称中心吗?
342900167640
(2)先将方格纸中的图形向右平移3格,然后再向下平移2格.
327787047625
【难度】★★
【答案】
【解析】(1)
所以点为所求.
41275010541000
(2)
【总结】本题考查了中心对称及图形的平移.
235585015621000画出三角形关于直线的轴对称的三角形.
【难度】★★
【答案】见解析
【解析】
如图为所求.
【总结】本题考查了成轴对称图形的画法.
图是用两个如图所示的直角三角形拼得的新图形,其中是中心对称
图形的是______________;是轴对称的图形是______________.
3524250107950
1162050196850
190500191770
20789906350
(A) (B) (C) (D)
【难度】★★
【答案】;.
【解析】中心对称图形是指把一个图形绕一点旋转180度后能与自身重合;轴对称图形是
在平面内沿一条直线折叠,直线两旁的部分能够完全重合的图形.
【总结】本题考查了中心对称图形及轴对称图形的概念.
分解因式:.
【难度】★★★
【答案】
【解析】
【总结】本题考查了因式分解的整体换元思想,注意分解要彻底.
已知多项式,求此多项式取最小值时的值,并求出
此最小值.
【难度】★★★
【答案】;此时最小值为.
【解析】
,且 ,
,原多项式的最小值为,此时.
【总结】本题考查了完全平方公式的运用,注意配方思想的运用.
解方程:.
【难度】★★★
【答案】.
【解析】解:,即,所以,
所以 ,解得:.
【总结】本题考查了同底数幂的运用.
已知,求代数式的值.
【难度】★★★
【答案】.
【解析】解:由,得:,
所以原式.
【总结】本题考查了等式的变形及整体代入求值的运用.
试判断的值与的大小关系,并证明你的结论.
【难度】★★★
【答案】见解析.
【解析】解:
;
所以.
【总结】本题考查了作差法比较大小及平方差公式的运用.
阅读下列材料:
(1)用作差可以比较两数的大小,即:若,则;
(2)平方式具有非负性,即.
请根据材料信息,比较,的大小.
【难度】★★★
【答案】.
【解析】解:
;
∵, ,即;
,即.
【总结】本题考查了利用作差法比较两数的大小以及配完全平方的运用.
如图,将六个正方形无缝拼接在一起构成一个长方形,其中最小的一个正方形边
长为,求拼成的长方形面积.
349250054610【难度】★★★
【答案】.
【解析】解:设右下角两个相等的小正方形边长为.
由题意得:
解得:
即长方形长为,宽为,
所以面积为.
【总结】 本题考查了字母表示数的应用.
用四块如图1所示正方形瓷砖拼成一个新的正方形,请你在图2、图3、图4中各画一种拼法.要求:其中一个图形既是轴对称图形,又是中心对称图形;一个图形是轴对称图形,但不是中心对称图形;一个图形是中心对称图形,但不是轴对称图形.
0175260377190017526025146001752601257300175260
342900175260342900175260
34290045720图1
图1
148590076200图2
图2
400050076200图4
图4
274320076200图3
图3
【难度】★★
【答案】见解析
【解析】
【总结】本题考查了中心对称图形及轴对称图形的性质.
如图,在上找到、两点,且,在的左边,使四边形
3472180120650的周长最短.
【难度】★★★
【答案】见解析
【解析】过点作关于直线的对称点,过点作
,使得,连接交直线于
在直线上截取,则四边形的周长最短.
【总结】本题考查了点的对称及两点之间线段最短的应用.
同课章节目录
