五年级上册数学一课一练-3.4组合图形 北京版(含答案)
文档属性
| 名称 | 五年级上册数学一课一练-3.4组合图形 北京版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 95.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-20 15:37:49 | ||
图片预览


文档简介
五年级上册数学一课一练-3.4组合图形
一、单选题
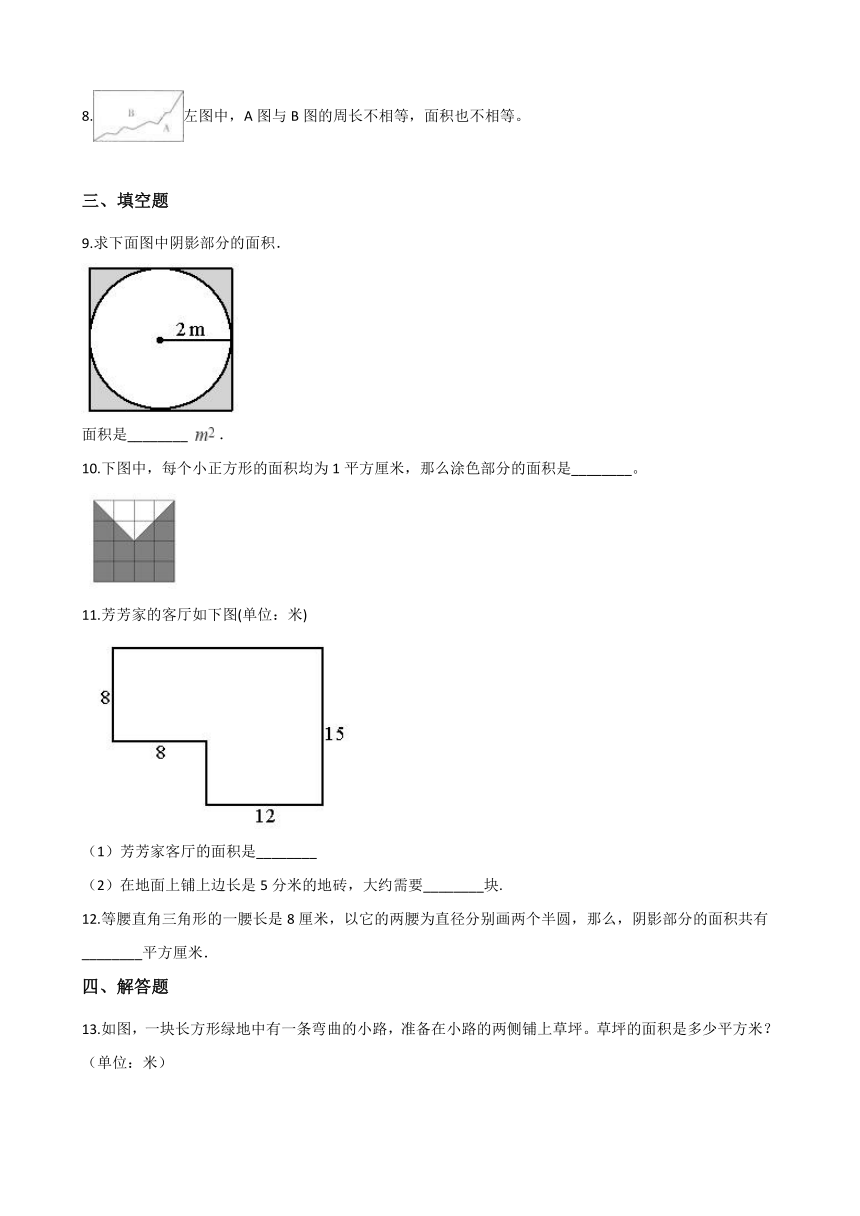
1.下面三幅图中,正方形一样大,则三个阴影部分的面积(??? )
A.?一样大??????????????????????B.?第一幅图最大??????????????????????C.?第二幅图最大??????????????????????D.?第三幅图最大
2.如图,图中圆的半径为r,长方形的长为2r,图中甲乙两块阴影部分的面积相比较,( ??)。
A.?甲的面积大??????????????????????????B.?乙的面积大??????????????????????????C.?一样大??????????????????????????D.?无法比较
3.将4个边长是1厘米的小正方形拼成一个长方形和一个正方形(如下图)。下面说法正确的是(? ?)。
A.?长方形的周长长,正方形的面积大。??????????????????B.?它们的面积相等,长方形的周长长。
C.?他们的周长和面积都相等????????????????????????????????????D.?它们的面积相等,正方形的周长长。
4.如图两个图中阴影部分的( )
A.?周长相等,面积不相等????????????B.?周长和面积都相等????????????C.?周长不相等,面积相等?????????
二、判断题
5.不规则图形用单位方格纸测面积,单位越小测得结果越准确
6.任何一个梯形都可以分成两个等高的三角形。
7.用4个边长1cm的小正方形拼成两个不同的图形,这两个图形的周长不同,面积也不同。
8.左图中,A图与B图的周长不相等,面积也不相等。
三、填空题
9.求下面图中阴影部分的面积.
面积是________ ?.
10.下图中,每个小正方形的面积均为1平方厘米,那么涂色部分的面积是________。
11.芳芳家的客厅如下图(单位:米)
(1)芳芳家客厅的面积是________
(2)在地面上铺上边长是5分米的地砖,大约需要________块.
12.等腰直角三角形的一腰长是8厘米,以它的两腰为直径分别画两个半圆,那么,阴影部分的面积共有________平方厘米.
四、解答题
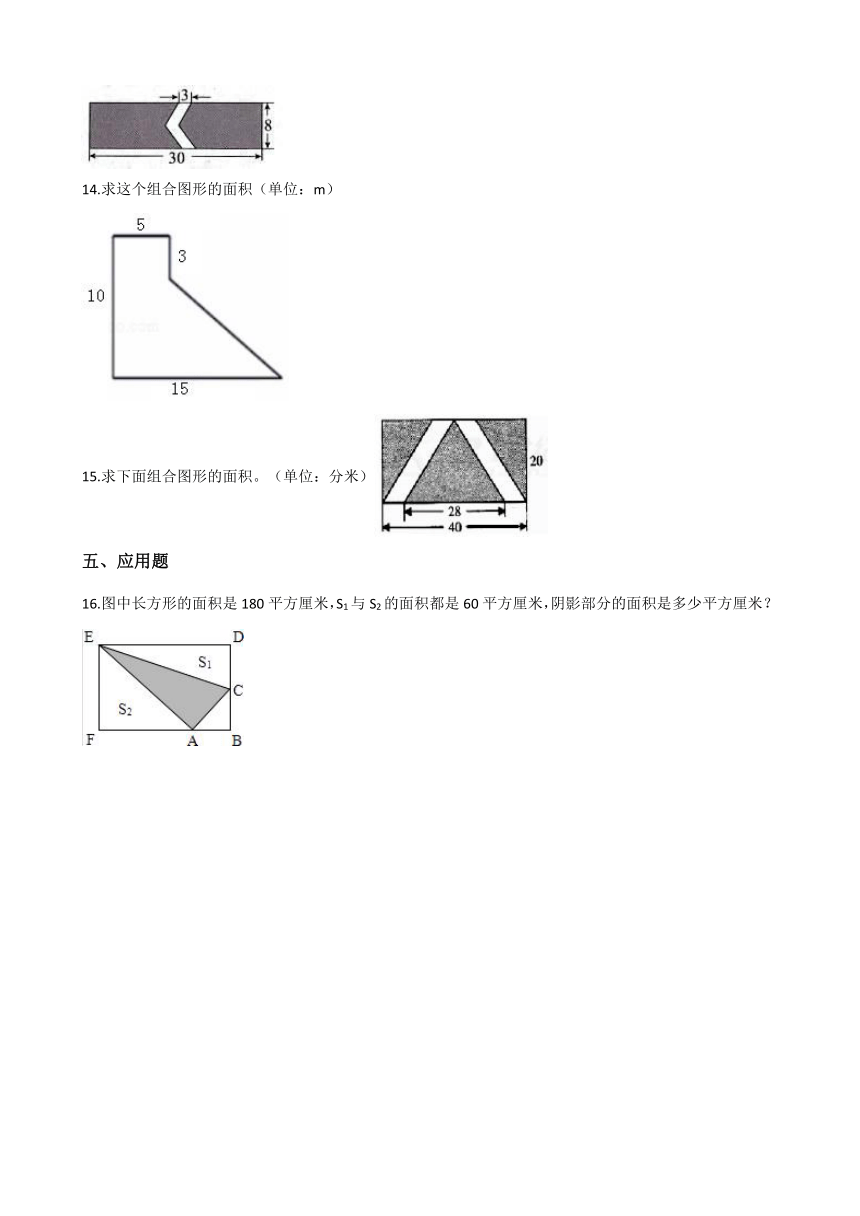
13.如图,一块长方形绿地中有一条弯曲的小路,准备在小路的两侧铺上草坪。草坪的面积是多少平方米?(单位:米)
14.求这个组合图形的面积(单位:m)
15.求下面组合图形的面积。(单位:分米)
五、应用题
16.图中长方形的面积是180平方厘米,S1与S2的面积都是60平方厘米,阴影部分的面积是多少平方厘米?
参考答案
一、单选题
1.【答案】 A
【解析】【解答】假设正方形的边长是4,
第一个图形:
4×4-3.14×(4÷2)?
=16-3.14×4
=16-12.56
=3.44
第二个图形:
4×4-3.14×(4÷4)?×4
=16-3.14×4
=16-12.56
=3.44
第三个图形:
4×4-3.14×4?÷4
=16-3.14×4
=16-12.56
=3.44
所以三个阴影部分的面积一样大.
故答案为:A
【分析】三个阴影部分的面积都是正方形面积减去内部空白部分的面积,假设出正方形的边长,然后根据正方形和圆面积公式分别计算阴影部分的面积并作出判断即可.
2.【答案】 A
【解析】【解答】解:甲的面积:π×r?×=2.355r?;乙的面积:2r×r=2r?;2.355r?>2r?,所以甲的面积大.
故答案为:A
【分析】甲的面积是所在圆面积的, 根据圆面积公式用含有r的式子表示甲的面积;根据长方形面积公式用式子表示出乙的面积;然后比较大小即可.
3.【答案】 B
【解析】【解答】解:它们的面积相等,长方形的周长长。
故答案为:B。
【分析】长方形和大正方形的都是由4个小正方形组成的,所以他们的面积相等;
长方形的周长=小正方形的边长×10,大正方形的周长=小正方形的边长×8,所以长方形的周长长。
4.【答案】C
【解析】【解答】解:由图可知:两个图形中的空白处均可组成一个完整的半径相等的圆,而正方形的面积相等,
根据等量减去等量差相等的原理得这两个图形中阴影部分的面积相等;
两个图形中阴影部分图形的周长不相等,第二个图形中阴影部分的周长多出两条边长.
故选:C.
【分析】从图中可以看出阴影部分的面积=正方形的面积﹣圆的面积.观察图形可发现:两个正方形是全等的,面积是相等;两个图形中空白部分可以组成一个完整的圆,根据圆的面积相等可得这两个图形中阴影部分的面积相等;而第一个图形中阴影部分的周长是直径为正方形的边长的圆的周长,第二个图形中阴影部分的周长是直径为正方形的边长的圆的周长+两条边长,所以周长不相等;据此选择.
二、判断题
5.【答案】 正确
【解析】【分析】单位越小越接近整数。
6.【答案】正确
【解析】【解答】根据梯形的定义可知,有一组对边平行的四边形叫平行四边形。因为当梯形分成两个三角形时是以梯形的上底和下底为三角形的一条底边,又因为梯形的上下底是一组平行线,所以它们之间的距离是相等的,所以任何一个梯形都可以分成两个等高的三角形的说法是正确的。
故答案为:正确。
【分析】根据梯形的定义可知,有一组对边平行的四边形叫平行四边形;因为当梯形分成两个三角形时是以梯形的上底和下底为三角形的一条底边,又因为梯形的上下底是一组平行线,所以它们之间的距离是相等的,由此判断即可。
7.【答案】 错误
【解析】【解答】解: 用4个边长1cm的小正方形拼成两个不同的图形 ,这两个图形的周长可能不同,但面积是相同的。
故答案为:错误。
【分析】 用4个边长1cm的小正方形拼成两个不同的图形 ,它们的面积都是1×1×4=4cm2 , 这两个图形都是由4个相同的正方形构成,所以面积是相同的;它们的周长可能会不同:当4个正方形排成一排时,它的周长是(1+4)×2=10cm,当这4个正方形上下各排2个时,它的周长是2×4=8cm。
8.【答案】错误
【解析】【解答】A图与B图的周长相等,面积不相等,原题说法错误.
故答案为:错误.
【分析】根据题意,A图的周长包括一条长和一条宽的长度之和及中间曲线的长度,B图的周长也包括一条长和一条宽的长度之和及中间曲线的长度,长方形的对边相等,所以周长相等,图形B的面积大于图形A的面积,据此解答.
三、填空题
9.【答案】3.44
【解析】【解答】2×2=4(米)
4×4-2×2×3.14=3.44(平方米)
故答案为:3.44
【分析】正方形的面积减去圆的面积.
10.【答案】 12平方厘米
【解析】【解答】解:采用数方格的方法判断,涂色部分的面积是12平方厘米。
故答案为:12平方厘米。
【分析】采用数方格的方法,数出整格的共10格,半格的共4格,相当于2个整格的,涂色部分共12格,也就是12平方厘米。
11.【答案】 (1)244平方米
(2)976
【解析】【解答】解:(1)面积:
8×8+15×12
=64+180
=244(平方米)
(2)5分米=0.5米,0.5×0.5=0.25(平方米),
244÷0.25=976(块)
故答案为:(1)244平方米;(2)976。
【分析】(1)客厅左边是正方形,右边是长方形,把这两部分面积相加就是总面积;
(2)用客厅的面积除以每块瓷砖的面积就是需要瓷砖的块数,注意统一单位。
12.【答案】18.24
【解析】【解答】解:3.14×(8÷2)2﹣8×8÷2,
=3.14×16﹣32,
=50.24﹣32,
=18.24(平方厘米);
答:阴影部分的面积共有18.24平方厘米,
故答案为:18.24
【分析】阴影部分的面积等于图中直径为8厘米的两个半圆的面积和与三角形ABC的面积之差.利用圆和三角形的面积公式代入数据即可解答.把阴影部分的面积转化到已知的规则图形中,利用面积公式进行解答.
四、解答题
13.【答案】解:(30-3)×8
=27×8
=216(平方米)
答:草坪的面积是216平方米。
【解析】【分析】草坪的面积实际就是长(30-3)米、宽8米的长方形面积。长方形面积=长×宽,根据长方形面积公式计算即可。
14.【答案】 解:5×3+(5+15)×(10﹣3)÷2
=15+20×7÷2
=15+70
=85(平方米)
答:这个组合图形的面积是85平方米。
【解析】【分析】这个组合图形的面积可以分为一个长方形和一个梯形两部分面积之和,即组合图形面积=长×宽+(上底+下底)×(高-长方形的宽)÷2,据此代入数据解答即可。
15.【答案】解:40×20-(40-28)×20
=800-240
=560(平方分米)
【解析】【分析】阴影部分的面积是长方形面积减去空白部分的面积,空白部分是两个相同的平行四边形,根据公式计算即可。
五、应用题
16.【答案】解:连接EB,则S△EFB=180÷2=90(平方厘米),
S△EAB=90﹣60=30(平方厘米),
所以AB:FB=1:3;
同理,BC:BD=1:3,
因此S△ABC= AB×BC,
= × FB× BD,
= FB×BD,
= ×180,
=10(平方厘米);
阴影部分的面积:180﹣60×2﹣10,
=180﹣120﹣10,
=60﹣10,
=50(平方厘米);
答:阴影部分的面积是50平方厘米
【解析】【分析】如图所示,阴影部分的面积=四边形EABC的面积﹣三角形ABC的面积,连接EB,则三角形EFB的面积为(180÷2=90平方厘米),则三角形EAB的面积为(90﹣60=30平方厘米),所以AB:FB=1:3;同理,BC:BD=1:3,则三角形ABC的面积= FB× BD× ,又因FB×BD=180平方厘米,从而可以求出三角形ABC的面积,也就能求出阴影部分的面积.解答此题的关键是:作出辅助线,利用等高的三角形的面积比就等于对应底边的比即可逐步求解.
.
一、单选题
1.下面三幅图中,正方形一样大,则三个阴影部分的面积(??? )
A.?一样大??????????????????????B.?第一幅图最大??????????????????????C.?第二幅图最大??????????????????????D.?第三幅图最大
2.如图,图中圆的半径为r,长方形的长为2r,图中甲乙两块阴影部分的面积相比较,( ??)。
A.?甲的面积大??????????????????????????B.?乙的面积大??????????????????????????C.?一样大??????????????????????????D.?无法比较
3.将4个边长是1厘米的小正方形拼成一个长方形和一个正方形(如下图)。下面说法正确的是(? ?)。
A.?长方形的周长长,正方形的面积大。??????????????????B.?它们的面积相等,长方形的周长长。
C.?他们的周长和面积都相等????????????????????????????????????D.?它们的面积相等,正方形的周长长。
4.如图两个图中阴影部分的( )
A.?周长相等,面积不相等????????????B.?周长和面积都相等????????????C.?周长不相等,面积相等?????????
二、判断题
5.不规则图形用单位方格纸测面积,单位越小测得结果越准确
6.任何一个梯形都可以分成两个等高的三角形。
7.用4个边长1cm的小正方形拼成两个不同的图形,这两个图形的周长不同,面积也不同。
8.左图中,A图与B图的周长不相等,面积也不相等。
三、填空题
9.求下面图中阴影部分的面积.
面积是________ ?.
10.下图中,每个小正方形的面积均为1平方厘米,那么涂色部分的面积是________。
11.芳芳家的客厅如下图(单位:米)
(1)芳芳家客厅的面积是________
(2)在地面上铺上边长是5分米的地砖,大约需要________块.
12.等腰直角三角形的一腰长是8厘米,以它的两腰为直径分别画两个半圆,那么,阴影部分的面积共有________平方厘米.
四、解答题
13.如图,一块长方形绿地中有一条弯曲的小路,准备在小路的两侧铺上草坪。草坪的面积是多少平方米?(单位:米)
14.求这个组合图形的面积(单位:m)
15.求下面组合图形的面积。(单位:分米)
五、应用题
16.图中长方形的面积是180平方厘米,S1与S2的面积都是60平方厘米,阴影部分的面积是多少平方厘米?
参考答案
一、单选题
1.【答案】 A
【解析】【解答】假设正方形的边长是4,
第一个图形:
4×4-3.14×(4÷2)?
=16-3.14×4
=16-12.56
=3.44
第二个图形:
4×4-3.14×(4÷4)?×4
=16-3.14×4
=16-12.56
=3.44
第三个图形:
4×4-3.14×4?÷4
=16-3.14×4
=16-12.56
=3.44
所以三个阴影部分的面积一样大.
故答案为:A
【分析】三个阴影部分的面积都是正方形面积减去内部空白部分的面积,假设出正方形的边长,然后根据正方形和圆面积公式分别计算阴影部分的面积并作出判断即可.
2.【答案】 A
【解析】【解答】解:甲的面积:π×r?×=2.355r?;乙的面积:2r×r=2r?;2.355r?>2r?,所以甲的面积大.
故答案为:A
【分析】甲的面积是所在圆面积的, 根据圆面积公式用含有r的式子表示甲的面积;根据长方形面积公式用式子表示出乙的面积;然后比较大小即可.
3.【答案】 B
【解析】【解答】解:它们的面积相等,长方形的周长长。
故答案为:B。
【分析】长方形和大正方形的都是由4个小正方形组成的,所以他们的面积相等;
长方形的周长=小正方形的边长×10,大正方形的周长=小正方形的边长×8,所以长方形的周长长。
4.【答案】C
【解析】【解答】解:由图可知:两个图形中的空白处均可组成一个完整的半径相等的圆,而正方形的面积相等,
根据等量减去等量差相等的原理得这两个图形中阴影部分的面积相等;
两个图形中阴影部分图形的周长不相等,第二个图形中阴影部分的周长多出两条边长.
故选:C.
【分析】从图中可以看出阴影部分的面积=正方形的面积﹣圆的面积.观察图形可发现:两个正方形是全等的,面积是相等;两个图形中空白部分可以组成一个完整的圆,根据圆的面积相等可得这两个图形中阴影部分的面积相等;而第一个图形中阴影部分的周长是直径为正方形的边长的圆的周长,第二个图形中阴影部分的周长是直径为正方形的边长的圆的周长+两条边长,所以周长不相等;据此选择.
二、判断题
5.【答案】 正确
【解析】【分析】单位越小越接近整数。
6.【答案】正确
【解析】【解答】根据梯形的定义可知,有一组对边平行的四边形叫平行四边形。因为当梯形分成两个三角形时是以梯形的上底和下底为三角形的一条底边,又因为梯形的上下底是一组平行线,所以它们之间的距离是相等的,所以任何一个梯形都可以分成两个等高的三角形的说法是正确的。
故答案为:正确。
【分析】根据梯形的定义可知,有一组对边平行的四边形叫平行四边形;因为当梯形分成两个三角形时是以梯形的上底和下底为三角形的一条底边,又因为梯形的上下底是一组平行线,所以它们之间的距离是相等的,由此判断即可。
7.【答案】 错误
【解析】【解答】解: 用4个边长1cm的小正方形拼成两个不同的图形 ,这两个图形的周长可能不同,但面积是相同的。
故答案为:错误。
【分析】 用4个边长1cm的小正方形拼成两个不同的图形 ,它们的面积都是1×1×4=4cm2 , 这两个图形都是由4个相同的正方形构成,所以面积是相同的;它们的周长可能会不同:当4个正方形排成一排时,它的周长是(1+4)×2=10cm,当这4个正方形上下各排2个时,它的周长是2×4=8cm。
8.【答案】错误
【解析】【解答】A图与B图的周长相等,面积不相等,原题说法错误.
故答案为:错误.
【分析】根据题意,A图的周长包括一条长和一条宽的长度之和及中间曲线的长度,B图的周长也包括一条长和一条宽的长度之和及中间曲线的长度,长方形的对边相等,所以周长相等,图形B的面积大于图形A的面积,据此解答.
三、填空题
9.【答案】3.44
【解析】【解答】2×2=4(米)
4×4-2×2×3.14=3.44(平方米)
故答案为:3.44
【分析】正方形的面积减去圆的面积.
10.【答案】 12平方厘米
【解析】【解答】解:采用数方格的方法判断,涂色部分的面积是12平方厘米。
故答案为:12平方厘米。
【分析】采用数方格的方法,数出整格的共10格,半格的共4格,相当于2个整格的,涂色部分共12格,也就是12平方厘米。
11.【答案】 (1)244平方米
(2)976
【解析】【解答】解:(1)面积:
8×8+15×12
=64+180
=244(平方米)
(2)5分米=0.5米,0.5×0.5=0.25(平方米),
244÷0.25=976(块)
故答案为:(1)244平方米;(2)976。
【分析】(1)客厅左边是正方形,右边是长方形,把这两部分面积相加就是总面积;
(2)用客厅的面积除以每块瓷砖的面积就是需要瓷砖的块数,注意统一单位。
12.【答案】18.24
【解析】【解答】解:3.14×(8÷2)2﹣8×8÷2,
=3.14×16﹣32,
=50.24﹣32,
=18.24(平方厘米);
答:阴影部分的面积共有18.24平方厘米,
故答案为:18.24
【分析】阴影部分的面积等于图中直径为8厘米的两个半圆的面积和与三角形ABC的面积之差.利用圆和三角形的面积公式代入数据即可解答.把阴影部分的面积转化到已知的规则图形中,利用面积公式进行解答.
四、解答题
13.【答案】解:(30-3)×8
=27×8
=216(平方米)
答:草坪的面积是216平方米。
【解析】【分析】草坪的面积实际就是长(30-3)米、宽8米的长方形面积。长方形面积=长×宽,根据长方形面积公式计算即可。
14.【答案】 解:5×3+(5+15)×(10﹣3)÷2
=15+20×7÷2
=15+70
=85(平方米)
答:这个组合图形的面积是85平方米。
【解析】【分析】这个组合图形的面积可以分为一个长方形和一个梯形两部分面积之和,即组合图形面积=长×宽+(上底+下底)×(高-长方形的宽)÷2,据此代入数据解答即可。
15.【答案】解:40×20-(40-28)×20
=800-240
=560(平方分米)
【解析】【分析】阴影部分的面积是长方形面积减去空白部分的面积,空白部分是两个相同的平行四边形,根据公式计算即可。
五、应用题
16.【答案】解:连接EB,则S△EFB=180÷2=90(平方厘米),
S△EAB=90﹣60=30(平方厘米),
所以AB:FB=1:3;
同理,BC:BD=1:3,
因此S△ABC= AB×BC,
= × FB× BD,
= FB×BD,
= ×180,
=10(平方厘米);
阴影部分的面积:180﹣60×2﹣10,
=180﹣120﹣10,
=60﹣10,
=50(平方厘米);
答:阴影部分的面积是50平方厘米
【解析】【分析】如图所示,阴影部分的面积=四边形EABC的面积﹣三角形ABC的面积,连接EB,则三角形EFB的面积为(180÷2=90平方厘米),则三角形EAB的面积为(90﹣60=30平方厘米),所以AB:FB=1:3;同理,BC:BD=1:3,则三角形ABC的面积= FB× BD× ,又因FB×BD=180平方厘米,从而可以求出三角形ABC的面积,也就能求出阴影部分的面积.解答此题的关键是:作出辅助线,利用等高的三角形的面积比就等于对应底边的比即可逐步求解.
.
