高二物理人教版选修3-4学案 第十五章 3 狭义相对论的其他结论 广义相对论简介 Word版含解析
文档属性
| 名称 | 高二物理人教版选修3-4学案 第十五章 3 狭义相对论的其他结论 广义相对论简介 Word版含解析 |

|
|
| 格式 | doc | ||
| 文件大小 | 639.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-20 14:54:16 | ||
图片预览


文档简介
如图所示,小河中流水的速度是3 m/s,小船顺流而下,由于划船,它相对于水的速度是1 m/s,那么船相对于河岸的速度是多少?假设水流的速度是0.7c(c为真空中的光速),而小船相对于水的划行速度是0.3c,还能这样求船相对于河岸的速度吗?
提示:如果物体的速度远小于真空中的光速,可以直接用u=u′+v,求对地速度u.其中v为参考系相对于地的速度,u′为物体相对参考系的速度,u为物体对地速度.但当速度接近真空中的光速时就要考虑相对论速度变换公式.
如果我们站在静止的电梯里,释放一块石子,石子由于受重力而自由下落,加速度大小为g(图a).如果该电梯处于没有引力的太空中,电梯以大小为g的加速度向上运动,人释放一块石子,电梯内的人看到石子做什么运动,其加速度是多少?(图b)
提示:我们在静止电梯里观察到的现象与在太空中加速上升的电梯中看到石子的运动没有区别,也就是说,实验不能告诉你,你是在没有重力的环境中做加速运动,还是在有重力的情况下处于静止.这说明非惯性参考系中出现的惯性力与引力在力学效应上是等效的.
考点一 狭义相对论的其他结论
1.相对论速度变换公式
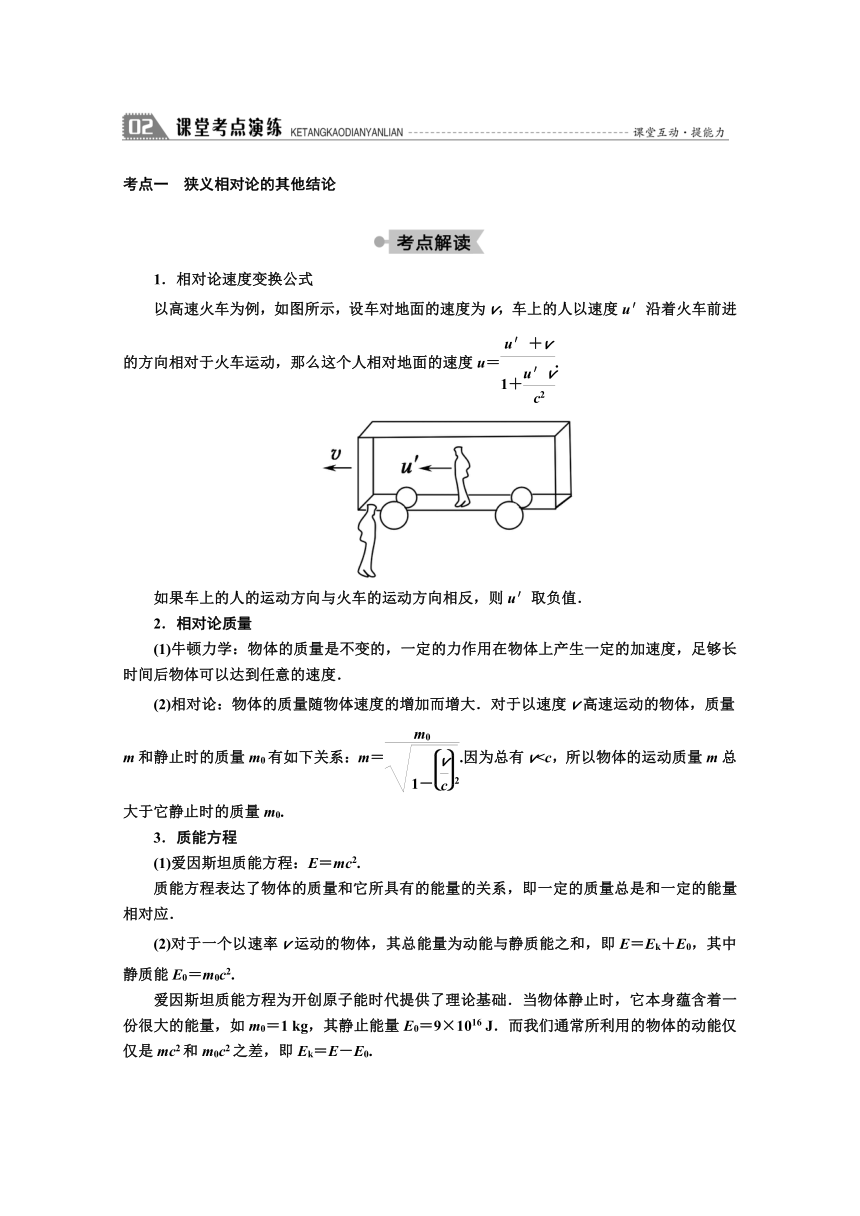
以高速火车为例,如图所示,设车对地面的速度为v,车上的人以速度u′沿着火车前进的方向相对于火车运动,那么这个人相对地面的速度u=.
如果车上的人的运动方向与火车的运动方向相反,则u′取负值.
2.相对论质量
(1)牛顿力学:物体的质量是不变的,一定的力作用在物体上产生一定的加速度,足够长时间后物体可以达到任意的速度.
(2)相对论:物体的质量随物体速度的增加而增大.对于以速度v高速运动的物体,质量m和静止时的质量m0有如下关系:m=.因为总有v3.质能方程
(1)爱因斯坦质能方程:E=mc2.
质能方程表达了物体的质量和它所具有的能量的关系,即一定的质量总是和一定的能量相对应.
(2)对于一个以速率v运动的物体,其总能量为动能与静质能之和,即E=Ek+E0,其中静质能E0=m0c2.
爱因斯坦质能方程为开创原子能时代提供了理论基础.当物体静止时,它本身蕴含着一份很大的能量,如m0=1 kg,其静止能量E0=9×1016 J.而我们通常所利用的物体的动能仅仅是mc2和m0c2之差,即Ek=E-E0.
在一切过程中,质量和能量是分别守恒的,只有在微观粒子的裂变和聚变过程中,有质量亏损的情况下,才会有质能方程的应用,即ΔE=Δmc2.
【例1】 若一宇宙飞船对地以速度v运动,宇航员在飞船内沿同方向测得光速为c,问在地上的观察者看来,光速应为v+c吗?
【导思】 根据相对论速度公式推导.
【解析】 由相对论速度变换公式u=,式中u′=c,代入公式中可得:u==c=c.可见:在地上观察者看来,光速应为c而不是v+c.
【答案】 不是,光速应为c.
【点拨】 应用速度变换公式要明确式中各物理量的意义.
一粒子以0.05c的速率相对实验室参考系运动.此粒子衰变时发射一个电子,电子相对于粒子的速度为0.8c,电子的衰变方向与粒子运动方向相同.求电子相对于实验室参考系的速度.
答案:0.817 c
解析:已知v=0.05c,u′=0.8c.由相对论速度变换公式得:
u===0.817c.
【例2】 在欧洲核子研究中心新建的大型强子对撞机中两个质子相向运动.假设每个质子相对实验室的速度都是c,在实验室观测,两个质子的总动能是多少?以一个质子为参考系,两个质子的总动能又是多少?(已知质子静质量为m)
【导思】 由题目条件可知,质子的速度接近光速,只能根据相对论的公式计算.
【解析】 质子以c运动时的质量为m′==m,在实验室观测,两个质子的总动能为
Ek1=2(m′c2-mc2)=2×=2.588mc2.
设两个质子分别为甲、乙,相对于乙质子,甲质子的速率是
u==c,
甲质子的质量是m″==9.526m.
因此,以乙质子为参考系,两质子的总动能即甲质子的动能为Ek2=m″c2-mc2=9.526mc2-mc2=8.526mc2.
【答案】 2.588 mc2 8.526 mc2
【点拨】 物理学的研究常常要利用高速粒子的相互撞击.通过此题我们看到,为使相互碰撞的粒子达到一定的相对速度,同时加速两束粒子,使它们迎头相撞,这样所需的能量要比只加速一束粒子,用它去轰击静止的靶所需的能量少,因而在技术上容易实现.这就是为什么有时候人们使用粒子对撞机,而不用普通加速器的原因.
1901年,德国科学家考夫曼在确定β射线比荷的实验中首先观测到电子比荷与速度有关,他假设电子的电荷不随速度改变,则电子的质量就要随速度的增加而增加.实验结果如图所示.请用质速关系公式计算电子在速度为0.6c和0.8c下的质量,并和实验数据对比.
答案:1.25m0 1.7m0 和实验数据比较,吻合得很好
解析:电子在速度为0.6c时的质量为
m1===1.25m0
电子在速度为0.8c时的质量为
m2==≈1.7m0
和实验数据比较,吻合得很好
考点二 广义相对论
1.狭义相对论无法解决的问题
(1)万有引力理论无法纳入狭义相对论框架.
(2)惯性参考系在狭义相对论中具有特殊的地位.
2.广义相对论的基本原理
(1)广义相对性原理:在任何参考系中,物理规律都是相同的.
(2)等效原理:一个均匀的引力场与一个做匀加速运动的参考系等价.
3.广义相对论的几个结论
(1)时空弯曲
广义相对论认为,时空不是平直的,而是弯曲或“扭曲”的.扭曲的基本原因在于时空和物质的质量或能量的分布.时空几乎在每一点上都是弯曲的,只有在没有质量的情况下,时空才没有弯曲.质量越大,时空弯曲的程度也就越大.
(2)光线弯曲
根据电磁理论和经典光学,在无障碍的情况下,光线是沿直线传播的.但按照爱因斯坦的广义相对论,在引力场存在的情况下,光线是沿弯曲的路径传播的.
(3)引力红移
根据爱因斯坦的广义相对论,在强引力场中,时钟要走得慢些,光在引力场中传播时,它的频率或波长会发生变化.理论计算表明,氢原子发射的光从太阳(引力强度大)传播到地球(引力强度小)时,它的频率比地球上的氢原子发射的光的频率低,这就是引力红移效应.
重难疑点辨析
爱因斯坦质能方程
1.爱因斯坦质能方程E=mc2
质能方程表达了物体的质量和它所具有的能量的关系:一定的质量总是和一定的能量相对应.
2.另一种表述形式为ΔE=Δmc2
它表明物体吸收和放出能量时,必伴随质量的增加或减少.这里,ΔE不仅可以表示机械能的改变,也可以代表因物体吸热或放热、吸收或辐射光子等引起的能量的变化.
具体从以下几个方面理解:
(1)静止物体的能量为E0=m0c2,这种能量叫做物体的静质能.每个有静质量的物体都具有静质能.
(2)对于一个以速率v运动的物体,其能量为
E=mc2=.
(3)静质量为m0、速率为v的物体的动能为Ek=E-E0=m0c2.
(4)由质能关系式可知ΔE=Δmc2.
【典例】 (多选)一个物体静止时质量为m0,能量为E0,速度为v时,质量为m,能量为E,动能为Ek,下列说法正确的是( )
A.物体速度为v时能量E=mc2
B.物体速度为v时的动能Ek=mc2
C.物体速度为v时的动能Ek=mv2
D.物体速度为v时的动能Ek=(m-m0)c2
【解析】 由爱因斯坦质能方程得E0=m0c2,E=mc2.在经典物理学中,速度为v时物体的动能Ek=m0v2,而这只是在v?c时的近似,在相对论中物体的动能Ek=E-E0=mc2-m0c2.故正确选项为A、D.
【答案】 AD
由相对论的质速关系m=知,物体以速度v运动时的质量m大于静止时的质量m0,且v越大,m与m0相差越大,微观粒子的运动速度很高,它的质量明显地大于静止质量,在粒子加速问题中注意考虑这一条件.
1.(多选)下列说法中正确的是( ABCD )
A.由于太阳引力场的影响,我们有可能看到太阳后面的恒星
B.强引力场作用可使光谱线向红端偏移
C.引力场越强的位置,时间进程越慢
D.由于物质的存在,实际空间是弯曲的
2.在适当的时候,通过仪器可以观察到太阳后面的恒星,这说明恒星发出的光( C )
A.经过太阳时发生了衍射
B.可以穿透太阳及其他障碍物
C.在太阳引力场作用下发生了弯曲
D.经过太阳表面的大气层时发生了折射
解析:恒星发出的光经过太阳周围强引力场时发生了弯曲.
3.一观察者测出电子质量为2m0,则电子速度为0.866c.(m0为电子的静止质量)
解析:电子运动时的质量是静止质量的2倍,运用相对论质量公式可解.m=2m0,代入相对论质量公式m=,可得2m0=,v=c≈0.866c.
4.设宇宙射线粒子的能量是其静止能量的k倍.则粒子运动时的质量等于其静止质量的k倍,粒子运动速度是光速的倍.
解析:由E=mc2知=,根据E=kE0可得m=km0;由
m=得,==k,
得v=c.
5.在外层空间的宇宙飞船上,你正在一个以加速度g=9.8 m/s2向头顶方向运动的电梯中,这时,你举起一个小球自由地丢下,请说明小球的运动情况.
答案:见解析
解析:由广义相对论的等效原理知,一个均匀的引力场与一个做匀加速运动的参考系等价.当电梯向头顶方向加速运动时,小球相对于电梯的加速度为g=9.8 m/s2,与在地球引力场中做自由落体运动相同.
提示:如果物体的速度远小于真空中的光速,可以直接用u=u′+v,求对地速度u.其中v为参考系相对于地的速度,u′为物体相对参考系的速度,u为物体对地速度.但当速度接近真空中的光速时就要考虑相对论速度变换公式.
如果我们站在静止的电梯里,释放一块石子,石子由于受重力而自由下落,加速度大小为g(图a).如果该电梯处于没有引力的太空中,电梯以大小为g的加速度向上运动,人释放一块石子,电梯内的人看到石子做什么运动,其加速度是多少?(图b)
提示:我们在静止电梯里观察到的现象与在太空中加速上升的电梯中看到石子的运动没有区别,也就是说,实验不能告诉你,你是在没有重力的环境中做加速运动,还是在有重力的情况下处于静止.这说明非惯性参考系中出现的惯性力与引力在力学效应上是等效的.
考点一 狭义相对论的其他结论
1.相对论速度变换公式
以高速火车为例,如图所示,设车对地面的速度为v,车上的人以速度u′沿着火车前进的方向相对于火车运动,那么这个人相对地面的速度u=.
如果车上的人的运动方向与火车的运动方向相反,则u′取负值.
2.相对论质量
(1)牛顿力学:物体的质量是不变的,一定的力作用在物体上产生一定的加速度,足够长时间后物体可以达到任意的速度.
(2)相对论:物体的质量随物体速度的增加而增大.对于以速度v高速运动的物体,质量m和静止时的质量m0有如下关系:m=.因为总有v
(1)爱因斯坦质能方程:E=mc2.
质能方程表达了物体的质量和它所具有的能量的关系,即一定的质量总是和一定的能量相对应.
(2)对于一个以速率v运动的物体,其总能量为动能与静质能之和,即E=Ek+E0,其中静质能E0=m0c2.
爱因斯坦质能方程为开创原子能时代提供了理论基础.当物体静止时,它本身蕴含着一份很大的能量,如m0=1 kg,其静止能量E0=9×1016 J.而我们通常所利用的物体的动能仅仅是mc2和m0c2之差,即Ek=E-E0.
在一切过程中,质量和能量是分别守恒的,只有在微观粒子的裂变和聚变过程中,有质量亏损的情况下,才会有质能方程的应用,即ΔE=Δmc2.
【例1】 若一宇宙飞船对地以速度v运动,宇航员在飞船内沿同方向测得光速为c,问在地上的观察者看来,光速应为v+c吗?
【导思】 根据相对论速度公式推导.
【解析】 由相对论速度变换公式u=,式中u′=c,代入公式中可得:u==c=c.可见:在地上观察者看来,光速应为c而不是v+c.
【答案】 不是,光速应为c.
【点拨】 应用速度变换公式要明确式中各物理量的意义.
一粒子以0.05c的速率相对实验室参考系运动.此粒子衰变时发射一个电子,电子相对于粒子的速度为0.8c,电子的衰变方向与粒子运动方向相同.求电子相对于实验室参考系的速度.
答案:0.817 c
解析:已知v=0.05c,u′=0.8c.由相对论速度变换公式得:
u===0.817c.
【例2】 在欧洲核子研究中心新建的大型强子对撞机中两个质子相向运动.假设每个质子相对实验室的速度都是c,在实验室观测,两个质子的总动能是多少?以一个质子为参考系,两个质子的总动能又是多少?(已知质子静质量为m)
【导思】 由题目条件可知,质子的速度接近光速,只能根据相对论的公式计算.
【解析】 质子以c运动时的质量为m′==m,在实验室观测,两个质子的总动能为
Ek1=2(m′c2-mc2)=2×=2.588mc2.
设两个质子分别为甲、乙,相对于乙质子,甲质子的速率是
u==c,
甲质子的质量是m″==9.526m.
因此,以乙质子为参考系,两质子的总动能即甲质子的动能为Ek2=m″c2-mc2=9.526mc2-mc2=8.526mc2.
【答案】 2.588 mc2 8.526 mc2
【点拨】 物理学的研究常常要利用高速粒子的相互撞击.通过此题我们看到,为使相互碰撞的粒子达到一定的相对速度,同时加速两束粒子,使它们迎头相撞,这样所需的能量要比只加速一束粒子,用它去轰击静止的靶所需的能量少,因而在技术上容易实现.这就是为什么有时候人们使用粒子对撞机,而不用普通加速器的原因.
1901年,德国科学家考夫曼在确定β射线比荷的实验中首先观测到电子比荷与速度有关,他假设电子的电荷不随速度改变,则电子的质量就要随速度的增加而增加.实验结果如图所示.请用质速关系公式计算电子在速度为0.6c和0.8c下的质量,并和实验数据对比.
答案:1.25m0 1.7m0 和实验数据比较,吻合得很好
解析:电子在速度为0.6c时的质量为
m1===1.25m0
电子在速度为0.8c时的质量为
m2==≈1.7m0
和实验数据比较,吻合得很好
考点二 广义相对论
1.狭义相对论无法解决的问题
(1)万有引力理论无法纳入狭义相对论框架.
(2)惯性参考系在狭义相对论中具有特殊的地位.
2.广义相对论的基本原理
(1)广义相对性原理:在任何参考系中,物理规律都是相同的.
(2)等效原理:一个均匀的引力场与一个做匀加速运动的参考系等价.
3.广义相对论的几个结论
(1)时空弯曲
广义相对论认为,时空不是平直的,而是弯曲或“扭曲”的.扭曲的基本原因在于时空和物质的质量或能量的分布.时空几乎在每一点上都是弯曲的,只有在没有质量的情况下,时空才没有弯曲.质量越大,时空弯曲的程度也就越大.
(2)光线弯曲
根据电磁理论和经典光学,在无障碍的情况下,光线是沿直线传播的.但按照爱因斯坦的广义相对论,在引力场存在的情况下,光线是沿弯曲的路径传播的.
(3)引力红移
根据爱因斯坦的广义相对论,在强引力场中,时钟要走得慢些,光在引力场中传播时,它的频率或波长会发生变化.理论计算表明,氢原子发射的光从太阳(引力强度大)传播到地球(引力强度小)时,它的频率比地球上的氢原子发射的光的频率低,这就是引力红移效应.
重难疑点辨析
爱因斯坦质能方程
1.爱因斯坦质能方程E=mc2
质能方程表达了物体的质量和它所具有的能量的关系:一定的质量总是和一定的能量相对应.
2.另一种表述形式为ΔE=Δmc2
它表明物体吸收和放出能量时,必伴随质量的增加或减少.这里,ΔE不仅可以表示机械能的改变,也可以代表因物体吸热或放热、吸收或辐射光子等引起的能量的变化.
具体从以下几个方面理解:
(1)静止物体的能量为E0=m0c2,这种能量叫做物体的静质能.每个有静质量的物体都具有静质能.
(2)对于一个以速率v运动的物体,其能量为
E=mc2=.
(3)静质量为m0、速率为v的物体的动能为Ek=E-E0=m0c2.
(4)由质能关系式可知ΔE=Δmc2.
【典例】 (多选)一个物体静止时质量为m0,能量为E0,速度为v时,质量为m,能量为E,动能为Ek,下列说法正确的是( )
A.物体速度为v时能量E=mc2
B.物体速度为v时的动能Ek=mc2
C.物体速度为v时的动能Ek=mv2
D.物体速度为v时的动能Ek=(m-m0)c2
【解析】 由爱因斯坦质能方程得E0=m0c2,E=mc2.在经典物理学中,速度为v时物体的动能Ek=m0v2,而这只是在v?c时的近似,在相对论中物体的动能Ek=E-E0=mc2-m0c2.故正确选项为A、D.
【答案】 AD
由相对论的质速关系m=知,物体以速度v运动时的质量m大于静止时的质量m0,且v越大,m与m0相差越大,微观粒子的运动速度很高,它的质量明显地大于静止质量,在粒子加速问题中注意考虑这一条件.
1.(多选)下列说法中正确的是( ABCD )
A.由于太阳引力场的影响,我们有可能看到太阳后面的恒星
B.强引力场作用可使光谱线向红端偏移
C.引力场越强的位置,时间进程越慢
D.由于物质的存在,实际空间是弯曲的
2.在适当的时候,通过仪器可以观察到太阳后面的恒星,这说明恒星发出的光( C )
A.经过太阳时发生了衍射
B.可以穿透太阳及其他障碍物
C.在太阳引力场作用下发生了弯曲
D.经过太阳表面的大气层时发生了折射
解析:恒星发出的光经过太阳周围强引力场时发生了弯曲.
3.一观察者测出电子质量为2m0,则电子速度为0.866c.(m0为电子的静止质量)
解析:电子运动时的质量是静止质量的2倍,运用相对论质量公式可解.m=2m0,代入相对论质量公式m=,可得2m0=,v=c≈0.866c.
4.设宇宙射线粒子的能量是其静止能量的k倍.则粒子运动时的质量等于其静止质量的k倍,粒子运动速度是光速的倍.
解析:由E=mc2知=,根据E=kE0可得m=km0;由
m=得,==k,
得v=c.
5.在外层空间的宇宙飞船上,你正在一个以加速度g=9.8 m/s2向头顶方向运动的电梯中,这时,你举起一个小球自由地丢下,请说明小球的运动情况.
答案:见解析
解析:由广义相对论的等效原理知,一个均匀的引力场与一个做匀加速运动的参考系等价.当电梯向头顶方向加速运动时,小球相对于电梯的加速度为g=9.8 m/s2,与在地球引力场中做自由落体运动相同.
