北师大版八年级上册1.2 一定是直角三角形吗 课件(22张)
文档属性
| 名称 | 北师大版八年级上册1.2 一定是直角三角形吗 课件(22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 717.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-21 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
1.2
一定是直角三角形吗
学习目标
1.经历勾股定理的逆定理的探索过程,进一步发展推理能力.(重点)
2.掌握勾股定理的逆定理,并能进行简单应用.(难点)
复习旧知
勾股定理:
直角三角形两直角边的平方和等于斜边的平方,如果用a,b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2。
A
B
C
a
b
c
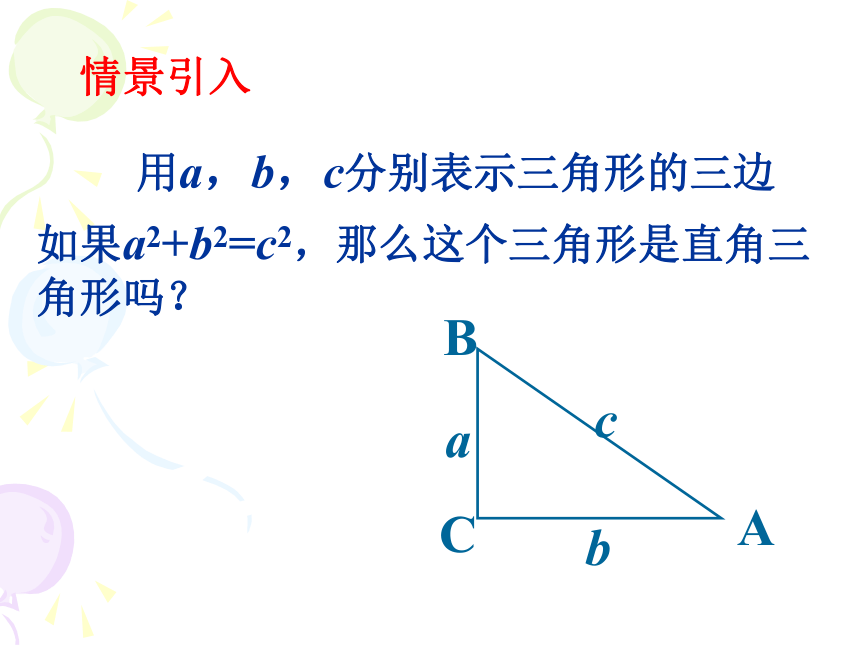
情景引入
如果a2+b2=c2,那么这个三角形是直角三角形吗?
A
B
C
a
b
c
用a,b,c分别表示三角形的三边
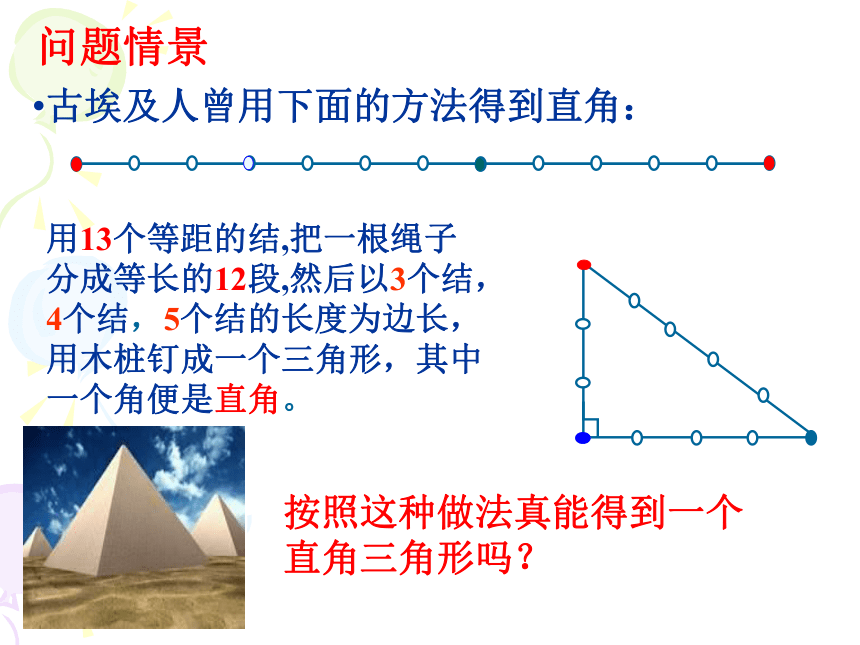
按照这种做法真能得到一个直角三角形吗?
古埃及人曾用下面的方法得到直角:
用13个等距的结,把一根绳子分成等长的12段,然后以3个结,4个结,5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角。
问题情景
合作探究
下面有三组数分别是一个三角形的三边长a,b,c:
①5,12,13;
②7,24,25;
③8,15,17.
回答这样两个问题:
1.这三组数都满足
a2+b2=c2吗?
2.分别以每组数为三边长作出三角形,它们都是直角三角形吗?
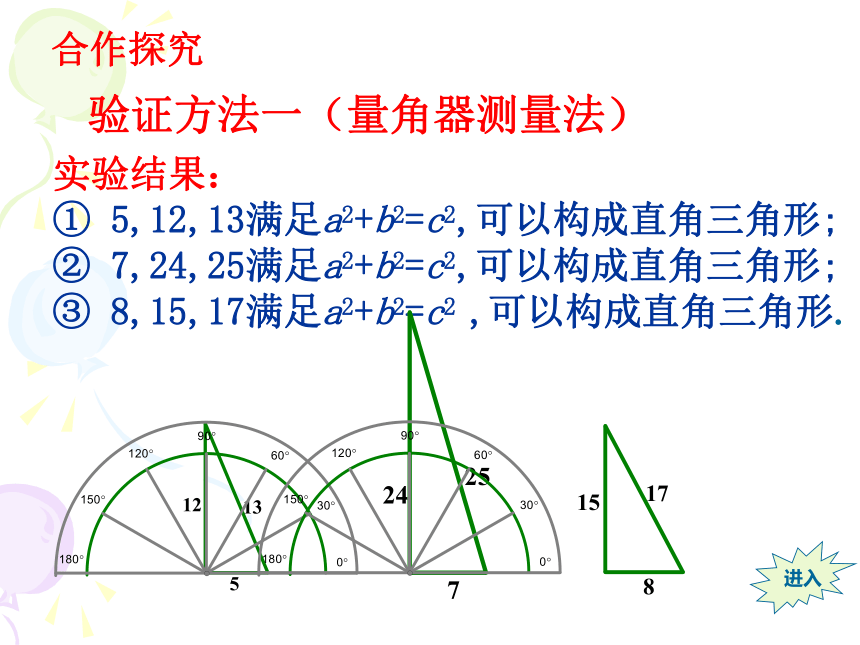
实验结果:
①
5,12,13满足a2+b2=c2,可以构成直角三角形;
②
7,24,25满足a2+b2=c2,可以构成直角三角形;
③
8,15,17满足a2+b2=c2
,可以构成直角三角形.
进入
合作探究
验证方法一(量角器测量法)
验证方法二
利用上节课(课本第6页)“议一议”的结论:锐角三角形和钝角三角形中,任意两边的平方和都不等于第三边的平方,所以三角形三边满足a2+b2=c2的关系的只能是直角三角形.
验证方法三
操作活动:以3和4为邻边,构造三角形,观察随着夹角的增加第三边的变化趋势,随着夹角的增加第三边的长度越来越大,夹角是直角时,第三边的长度等于5.
合作探究
在Rt△A1C1B1中,由勾股定理得:
a2+b2=
A1B12=AB2
.
∴
A1B1=AB
.
∴
△ABC≌△A1B1C1
(SSS)
∴
∠C=∠C1=90°
.
∴
△ABC是直角三角形.
a
c
b
A
C
B
C1
M
N
B1
A1
已知:在△ABC中,三边长分别为a,b,c,且a2+b2=c2.
你能否判断
△ABC是直角三角形?并说明理由.
简要说明:
作一个直角∠MC1N,
在C1M上截取C1B1=a=CB,
在C1N上截取C1A1=b=CA,
连接A1B1.
验证方法四:论证法
合作探究
1.勾股定理的逆定理:
(1)文字描述:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
合作探究
结论:
∵在△ABC中,a2+b2=c2
(2)符号语言:
∴∠C=90°(勾股定理逆定理)
A
B
C
a
b
c
2.勾股数:满足a2+b2=c2的三个正整数,称为勾股数。
1、勾股数是正整数
2、勾股数扩大相同整数倍数后,仍为勾股数。
你还能找出哪些勾股数呢?
常见勾股数:
3,4,5;5,12,13;6,8,10;7,24,25;8,15,17;9,40,41;10,24,26等等.
例1:给出下列说法:
①如果a,b,c为一组勾股数,那么4a,4b,4c仍是一组勾股数;
②如果直角三角形的两边长分别是3和4,那么另一边长的平方必为25;
③如果一个三角形的三边长分别是12,25,21,那么此三角形必是直角三角形;
④一个等腰直角三角形的三边长分别是a,b,c,其中a是斜边长,那么a2∶b2∶c2=2∶1∶1.
其中正确的是( )
A.①②
B.①③
C.①④
D.②④
C
例2.一个零件的形状如图(a)所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边尺寸如图(b)所示,这个零件合格吗?
A
B
C
D
A
B
C
D
3
4
5
12
13
(a)
(b)
例3
:判断满足下列条件的三角形是不是直角三角形:
(1)在△ABC中,∠A=25°,∠C=65°;
(2)在△ABC中,AC=12,AB=20,BC=16;
(3)一个三角形的三边a,b,c满足a:b:c=3:4:5.
解:(1)在△ABC中,∵∠A+∠B+∠C=180°,
∴∠B=180°-25°-65°=90°.
∴△ABC是直角三角形.
(2)在△ABC中,∵AC2+BC2=122+162=202=AB2,
∴△ABC是直角三角形,且∠C为直角.
(3)设a=3k,则b=4k,c=5k.
∵(3k)2+(4k)2=25k2
c2=
(5k)2
,
即a2+b2=c2
∴△ABC是直角三角形
.
C
变式1:
已知△ABC,AB=n?-1,BC=2n,AC=n?+1(n为
大于1的正整数).试问△ABC是直角三角形吗?若是,
哪一条边所对的角是直角?请说明理由
解:∵AB?+BC?
=(n?-1)?+(2n)?
=n4
-2n?+1+4n?
=n4
+2n?+1
=(n?+1)?
=AC?,
∴△ABC直角三角形,边AC所对的角是直角.
先确定AB、BC、AC、
的大小
变式2:
若三角形ABC的三边
a,b,c
满足a2+b2+c2+50=6a+8b+10c.
试判断△ABC的形状.
解:∵
a2+b2+c2+50=6a+8b+10c
∴
a2-6a+9+b2-8b+16+c2-10c+25=0.
即
(a-3)?+
(b-4)?+
(c-5)?=0.
∴
a=3,
b=4,
c=5
即
a2+b2=c2.
∴△ABC直角三角形.
例4:下列数组中,不是勾股数的是( )
A.3,4,5
B.9,12,15
C.7,24,25
D.1.5,2,2.5
D
注意:判断一组数是否为勾股数的一般步骤:
(1)“看”
看是不是三个正整数.
(2)“找”
找最大数.
(3)“算”
计算最大数的平方与两个较小数的平方和.
(4)“判”
若两者相等,则这三个数是一组勾股数;
否则,不是一组勾股数.
例5.如图,每个小方格都是边长为1的正方形,
(1)求四边形ABCD的面积;
(2)求∠ABC的度数.
∵AB2=22+42=20,BC2=12+22=5,AC2=52=25,
∴AB2+BC2=AC2.
∴∠ABC=90°.
练习.如图,哪些是直角三角形,哪些不是,说说你的理由?
①
②
③
④
⑤
⑥
解:
④⑤是直角三角形
①②③⑥不是直角三角形
只要看两条较小边的平方和是否等于最大边的平方。
例6:在正方形ABCD中,F是CD的中点,E为BC上一点,且CE=
CB,试判断AF与EF的位置关系,并说明理由.
解:AF⊥EF.设正方形的边长为4a,
则EC=a,BE=3a,CF=DF=2a.
在Rt△ABE中,得AE2=AB2+BE2=16a2+9a2=25a2.
在Rt△CEF中,得EF2=CE2+CF2=a2+4a2=5a2.
在Rt△ADF中,得AF2=AD2+DF2=16a2+4a2=20a2.
在△AEF中,AE2=EF2+AF2,
∴△AEF为直角三角形,且AE为斜边.
∴∠AFE=90°,即AF⊥EF.
1.“勾股定理”逆定理:
(1)文字语言:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形。
A
B
C
a
b
c
(2)符号语言:
∴∠C=90°(勾股定理逆定理)
2.“勾股定理”逆定理的应用:
已知三边特殊关系,判定直角三角形。
3.“勾股数”的定义:
满足a2+b2=c2的三个正整数,称为勾股数。
课堂小结
∵在△ABC中,a2+b2=c2
1.2
一定是直角三角形吗
学习目标
1.经历勾股定理的逆定理的探索过程,进一步发展推理能力.(重点)
2.掌握勾股定理的逆定理,并能进行简单应用.(难点)
复习旧知
勾股定理:
直角三角形两直角边的平方和等于斜边的平方,如果用a,b和c分别表示直角三角形的两直角边和斜边,那么a2+b2=c2。
A
B
C
a
b
c
情景引入
如果a2+b2=c2,那么这个三角形是直角三角形吗?
A
B
C
a
b
c
用a,b,c分别表示三角形的三边
按照这种做法真能得到一个直角三角形吗?
古埃及人曾用下面的方法得到直角:
用13个等距的结,把一根绳子分成等长的12段,然后以3个结,4个结,5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角。
问题情景
合作探究
下面有三组数分别是一个三角形的三边长a,b,c:
①5,12,13;
②7,24,25;
③8,15,17.
回答这样两个问题:
1.这三组数都满足
a2+b2=c2吗?
2.分别以每组数为三边长作出三角形,它们都是直角三角形吗?
实验结果:
①
5,12,13满足a2+b2=c2,可以构成直角三角形;
②
7,24,25满足a2+b2=c2,可以构成直角三角形;
③
8,15,17满足a2+b2=c2
,可以构成直角三角形.
进入
合作探究
验证方法一(量角器测量法)
验证方法二
利用上节课(课本第6页)“议一议”的结论:锐角三角形和钝角三角形中,任意两边的平方和都不等于第三边的平方,所以三角形三边满足a2+b2=c2的关系的只能是直角三角形.
验证方法三
操作活动:以3和4为邻边,构造三角形,观察随着夹角的增加第三边的变化趋势,随着夹角的增加第三边的长度越来越大,夹角是直角时,第三边的长度等于5.
合作探究
在Rt△A1C1B1中,由勾股定理得:
a2+b2=
A1B12=AB2
.
∴
A1B1=AB
.
∴
△ABC≌△A1B1C1
(SSS)
∴
∠C=∠C1=90°
.
∴
△ABC是直角三角形.
a
c
b
A
C
B
C1
M
N
B1
A1
已知:在△ABC中,三边长分别为a,b,c,且a2+b2=c2.
你能否判断
△ABC是直角三角形?并说明理由.
简要说明:
作一个直角∠MC1N,
在C1M上截取C1B1=a=CB,
在C1N上截取C1A1=b=CA,
连接A1B1.
验证方法四:论证法
合作探究
1.勾股定理的逆定理:
(1)文字描述:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
合作探究
结论:
∵在△ABC中,a2+b2=c2
(2)符号语言:
∴∠C=90°(勾股定理逆定理)
A
B
C
a
b
c
2.勾股数:满足a2+b2=c2的三个正整数,称为勾股数。
1、勾股数是正整数
2、勾股数扩大相同整数倍数后,仍为勾股数。
你还能找出哪些勾股数呢?
常见勾股数:
3,4,5;5,12,13;6,8,10;7,24,25;8,15,17;9,40,41;10,24,26等等.
例1:给出下列说法:
①如果a,b,c为一组勾股数,那么4a,4b,4c仍是一组勾股数;
②如果直角三角形的两边长分别是3和4,那么另一边长的平方必为25;
③如果一个三角形的三边长分别是12,25,21,那么此三角形必是直角三角形;
④一个等腰直角三角形的三边长分别是a,b,c,其中a是斜边长,那么a2∶b2∶c2=2∶1∶1.
其中正确的是( )
A.①②
B.①③
C.①④
D.②④
C
例2.一个零件的形状如图(a)所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边尺寸如图(b)所示,这个零件合格吗?
A
B
C
D
A
B
C
D
3
4
5
12
13
(a)
(b)
例3
:判断满足下列条件的三角形是不是直角三角形:
(1)在△ABC中,∠A=25°,∠C=65°;
(2)在△ABC中,AC=12,AB=20,BC=16;
(3)一个三角形的三边a,b,c满足a:b:c=3:4:5.
解:(1)在△ABC中,∵∠A+∠B+∠C=180°,
∴∠B=180°-25°-65°=90°.
∴△ABC是直角三角形.
(2)在△ABC中,∵AC2+BC2=122+162=202=AB2,
∴△ABC是直角三角形,且∠C为直角.
(3)设a=3k,则b=4k,c=5k.
∵(3k)2+(4k)2=25k2
c2=
(5k)2
,
即a2+b2=c2
∴△ABC是直角三角形
.
C
变式1:
已知△ABC,AB=n?-1,BC=2n,AC=n?+1(n为
大于1的正整数).试问△ABC是直角三角形吗?若是,
哪一条边所对的角是直角?请说明理由
解:∵AB?+BC?
=(n?-1)?+(2n)?
=n4
-2n?+1+4n?
=n4
+2n?+1
=(n?+1)?
=AC?,
∴△ABC直角三角形,边AC所对的角是直角.
先确定AB、BC、AC、
的大小
变式2:
若三角形ABC的三边
a,b,c
满足a2+b2+c2+50=6a+8b+10c.
试判断△ABC的形状.
解:∵
a2+b2+c2+50=6a+8b+10c
∴
a2-6a+9+b2-8b+16+c2-10c+25=0.
即
(a-3)?+
(b-4)?+
(c-5)?=0.
∴
a=3,
b=4,
c=5
即
a2+b2=c2.
∴△ABC直角三角形.
例4:下列数组中,不是勾股数的是( )
A.3,4,5
B.9,12,15
C.7,24,25
D.1.5,2,2.5
D
注意:判断一组数是否为勾股数的一般步骤:
(1)“看”
看是不是三个正整数.
(2)“找”
找最大数.
(3)“算”
计算最大数的平方与两个较小数的平方和.
(4)“判”
若两者相等,则这三个数是一组勾股数;
否则,不是一组勾股数.
例5.如图,每个小方格都是边长为1的正方形,
(1)求四边形ABCD的面积;
(2)求∠ABC的度数.
∵AB2=22+42=20,BC2=12+22=5,AC2=52=25,
∴AB2+BC2=AC2.
∴∠ABC=90°.
练习.如图,哪些是直角三角形,哪些不是,说说你的理由?
①
②
③
④
⑤
⑥
解:
④⑤是直角三角形
①②③⑥不是直角三角形
只要看两条较小边的平方和是否等于最大边的平方。
例6:在正方形ABCD中,F是CD的中点,E为BC上一点,且CE=
CB,试判断AF与EF的位置关系,并说明理由.
解:AF⊥EF.设正方形的边长为4a,
则EC=a,BE=3a,CF=DF=2a.
在Rt△ABE中,得AE2=AB2+BE2=16a2+9a2=25a2.
在Rt△CEF中,得EF2=CE2+CF2=a2+4a2=5a2.
在Rt△ADF中,得AF2=AD2+DF2=16a2+4a2=20a2.
在△AEF中,AE2=EF2+AF2,
∴△AEF为直角三角形,且AE为斜边.
∴∠AFE=90°,即AF⊥EF.
1.“勾股定理”逆定理:
(1)文字语言:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形。
A
B
C
a
b
c
(2)符号语言:
∴∠C=90°(勾股定理逆定理)
2.“勾股定理”逆定理的应用:
已知三边特殊关系,判定直角三角形。
3.“勾股数”的定义:
满足a2+b2=c2的三个正整数,称为勾股数。
课堂小结
∵在△ABC中,a2+b2=c2
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
