沪科版数学八年级上册:13.1三角形中的边角关系课件(第二课时 16张)
文档属性
| 名称 | 沪科版数学八年级上册:13.1三角形中的边角关系课件(第二课时 16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 522.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-21 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
13.1三角形中的边角关系
(第二课时)
回忆过去
1、画一个△ABC,它的三个内角有什么关
系?
2、拿出你事先准备好的三角形纸片进行折
叠,互相交流你们的发现?
3、把△ABC的三个角剪下来并把它们拼
在一起,交流你们的发现。
操作
拿出你事先准备好的三角形纸片进行
折叠,互相交流你们的发现?
剪拼:把△ABC的三个角剪下来并把它们拼在一起,交流你们的发现。
动手操作
通过测量、折叠、剪拼实验,我们得出结论:三角形的内角和是(
)
180°
(1)一个三角形中最多有
个直角?
为什么?并画出一个这样的三角形
(2)一个三角形中最多有
个钝角?
为什么?并画出一个这样的三角形
(3)一个三角形中能否有三个内角都是锐角?若有,请你画出一个这样的三角形。
通过以上讨论:
你认为三角形按角如何分类呢?
1
1
议一议
画一画
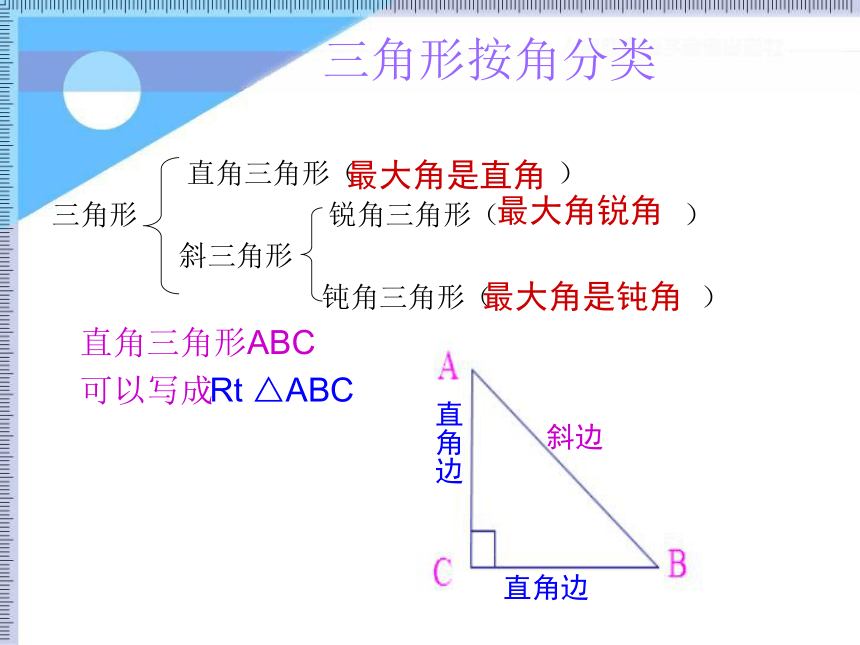
三角形按角分类
直角三角形(
)
三角形
锐角三角形(
)
斜三角形
钝角三角形(
)
直角三角形ABC
可以写成
最大角锐角
最大角是直角
最大角是钝角
Rt
△ABC
直角边
直角边
斜边
1.在△ABC中,∠A=700
,∠C=500。则∠B=
。
2.
如图,一块三角形木板的残余部分,量
得∠A=1100,∠B=400,这块木板的另
一个角是
。
3.在下列横线上,分别填上“锐角”、“直角”或“钝角”。
(1)在△ABC中,∠A=∠B+∠C
,则△ABC是
三角形
(2)在△ABC中,∠A+∠B=200,
则△ABC是
三角形
(3)在△ABC中,∠A=400,∠B=∠C,则△ABC是
三角形
练一练
直角
钝角
锐角
600
300
例1:已知:如图所示,△ABC中,
BD⊥AC,垂足为D。∠ABD=54°,
∠DBC=18°。求∠A和∠C的度数。
例2:在△ABC中,∠A︰∠B︰∠C=1︰2︰3,
那么这个三角形是什么样的三角形呢?
(按角分类)
应用新知
例1:已知:如图所示,△ABC中,BD⊥AC,垂足为D。∠ABD=54°,∠DBC=18°。
求∠A和∠C的度数。
解:由于BD⊥AC,(
已知
)
所以∠ADB=∠CDB=900
在△ABD中,
∠A+∠ADB+∠ABD=1800(
)
∠ABD=540,∠ADB=900(
)
∠A=1800-∠ADB-∠ABD=1800-900-540=360
在
△ABC中,
∠C=1800-∠A-(∠ABD+
∠DBC)
=1800-360-(540+180
)=720
三角形的三个内角和等于
1800
已知
例2:在△ABC中,∠A︰∠B︰∠C=1︰2︰3,
那么这个三角形是什么样的三角形呢?
(按角分类)
解:由题意设∠A=x,则∠B=2x,
∠C=
3x。
因为∠A+∠B+∠C=
1800
所以x+2x+3x=
1800
X=300
所以∠A=300∠B=600
∠C=900
因此,△ABC是直角三角形
例题解析
1、在△ABC中:
(1)已知:∠A=1050,∠B-∠C=150,则∠C=(
)
(2)已知:∠A︰∠B︰∠C=3︰4︰5,则∠C=(
)
(3)在△ABC中,
∠A=1000
,
∠B=
400
+∠C
,则∠C=
(
)
2、如图,∠ACB=900,CD⊥AB,垂足是D。
(1)写出图中所有直角三角形,并指出
它们的斜边;
(2)写出图中所有相等的角。
3、已知,如图,在△ABC中,∠B=700,
∠BAC=460,AD⊥BC,垂足是D。
求∠CAD的度数。
能力提升
300
750
200
Rt
△ABC
Rt
△BDC
Rt
△ADC
∠A=∠BCD
∠ACB=∠CDB=
∠
CDA
∠B=
∠ACD
跃一跃
1.一块大型模板,设计要求BA与CD相交成300角,DA与CB相交成200角,怎样通过测量∠A、∠B、∠C、∠D的度数来检验模板是否合格?
通过本节课的学习,你学到了什么?有什么收获?
还有哪些问题需要我们共同解决,请提出来。
小结反思:
选做题:
已知:如图,AB∥CD。
那么∠A与∠CED+∠D
相等吗?为什么?
作业
必做题:教材第74页,习题
7.2
2、3、5
敬请批评指正
13.1三角形中的边角关系
(第二课时)
回忆过去
1、画一个△ABC,它的三个内角有什么关
系?
2、拿出你事先准备好的三角形纸片进行折
叠,互相交流你们的发现?
3、把△ABC的三个角剪下来并把它们拼
在一起,交流你们的发现。
操作
拿出你事先准备好的三角形纸片进行
折叠,互相交流你们的发现?
剪拼:把△ABC的三个角剪下来并把它们拼在一起,交流你们的发现。
动手操作
通过测量、折叠、剪拼实验,我们得出结论:三角形的内角和是(
)
180°
(1)一个三角形中最多有
个直角?
为什么?并画出一个这样的三角形
(2)一个三角形中最多有
个钝角?
为什么?并画出一个这样的三角形
(3)一个三角形中能否有三个内角都是锐角?若有,请你画出一个这样的三角形。
通过以上讨论:
你认为三角形按角如何分类呢?
1
1
议一议
画一画
三角形按角分类
直角三角形(
)
三角形
锐角三角形(
)
斜三角形
钝角三角形(
)
直角三角形ABC
可以写成
最大角锐角
最大角是直角
最大角是钝角
Rt
△ABC
直角边
直角边
斜边
1.在△ABC中,∠A=700
,∠C=500。则∠B=
。
2.
如图,一块三角形木板的残余部分,量
得∠A=1100,∠B=400,这块木板的另
一个角是
。
3.在下列横线上,分别填上“锐角”、“直角”或“钝角”。
(1)在△ABC中,∠A=∠B+∠C
,则△ABC是
三角形
(2)在△ABC中,∠A+∠B=200,
则△ABC是
三角形
(3)在△ABC中,∠A=400,∠B=∠C,则△ABC是
三角形
练一练
直角
钝角
锐角
600
300
例1:已知:如图所示,△ABC中,
BD⊥AC,垂足为D。∠ABD=54°,
∠DBC=18°。求∠A和∠C的度数。
例2:在△ABC中,∠A︰∠B︰∠C=1︰2︰3,
那么这个三角形是什么样的三角形呢?
(按角分类)
应用新知
例1:已知:如图所示,△ABC中,BD⊥AC,垂足为D。∠ABD=54°,∠DBC=18°。
求∠A和∠C的度数。
解:由于BD⊥AC,(
已知
)
所以∠ADB=∠CDB=900
在△ABD中,
∠A+∠ADB+∠ABD=1800(
)
∠ABD=540,∠ADB=900(
)
∠A=1800-∠ADB-∠ABD=1800-900-540=360
在
△ABC中,
∠C=1800-∠A-(∠ABD+
∠DBC)
=1800-360-(540+180
)=720
三角形的三个内角和等于
1800
已知
例2:在△ABC中,∠A︰∠B︰∠C=1︰2︰3,
那么这个三角形是什么样的三角形呢?
(按角分类)
解:由题意设∠A=x,则∠B=2x,
∠C=
3x。
因为∠A+∠B+∠C=
1800
所以x+2x+3x=
1800
X=300
所以∠A=300∠B=600
∠C=900
因此,△ABC是直角三角形
例题解析
1、在△ABC中:
(1)已知:∠A=1050,∠B-∠C=150,则∠C=(
)
(2)已知:∠A︰∠B︰∠C=3︰4︰5,则∠C=(
)
(3)在△ABC中,
∠A=1000
,
∠B=
400
+∠C
,则∠C=
(
)
2、如图,∠ACB=900,CD⊥AB,垂足是D。
(1)写出图中所有直角三角形,并指出
它们的斜边;
(2)写出图中所有相等的角。
3、已知,如图,在△ABC中,∠B=700,
∠BAC=460,AD⊥BC,垂足是D。
求∠CAD的度数。
能力提升
300
750
200
Rt
△ABC
Rt
△BDC
Rt
△ADC
∠A=∠BCD
∠ACB=∠CDB=
∠
CDA
∠B=
∠ACD
跃一跃
1.一块大型模板,设计要求BA与CD相交成300角,DA与CB相交成200角,怎样通过测量∠A、∠B、∠C、∠D的度数来检验模板是否合格?
通过本节课的学习,你学到了什么?有什么收获?
还有哪些问题需要我们共同解决,请提出来。
小结反思:
选做题:
已知:如图,AB∥CD。
那么∠A与∠CED+∠D
相等吗?为什么?
作业
必做题:教材第74页,习题
7.2
2、3、5
敬请批评指正
