北师大版八年级数学上册 4.4一次函数的应用 同步练习(word版 含答案)
文档属性
| 名称 | 北师大版八年级数学上册 4.4一次函数的应用 同步练习(word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 479.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-21 00:00:00 | ||
图片预览



文档简介
4.4一次函数的应用第1课时同步练习
一、选择题
1、某公司市场营销部的个人月收入与其每月的销售量成一次函数关系,
其图象如上图所示,由图中给出的信息可知,营销人员没有销售时(最低工资)的收入是(
)
A.310元
B.300元
C.290元
D.280元
2、已知一次函数y=kx-4(k<0)的图象与两坐标轴所围成的三角形的面积等于4,则该一次函数的表达式为( )
A.y=-x-4
B.y=-2x-4
C.y=-3x+4
D.y=-3x-4
3、小明和哥哥从家里出发去买书,从家出发走了20分钟到一个离家1
000
m的书店.小明买了书后随即按原路返回;哥哥看了20分钟书后,用15分钟返家.下面的图象表示哥哥离家时间与距离之间关系的是( )
4、一次函数的图象经过点A和B两点,那么该函数的表达式是(
)
A.
B.
C.
D.
5.正比例函数的图象经过点,那么它一定经过的点是(
)
A.
B.
C.
D.
6、甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20
km.他们前进的路程为s(单位:km),甲出发后的时间为t(单位:h),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息,下列说法正确的是( )
A.甲的速度是4
km/h
B.乙的速度是10
km/h
C.乙比甲晚出发1
h
D.甲比乙晚到B地3
h
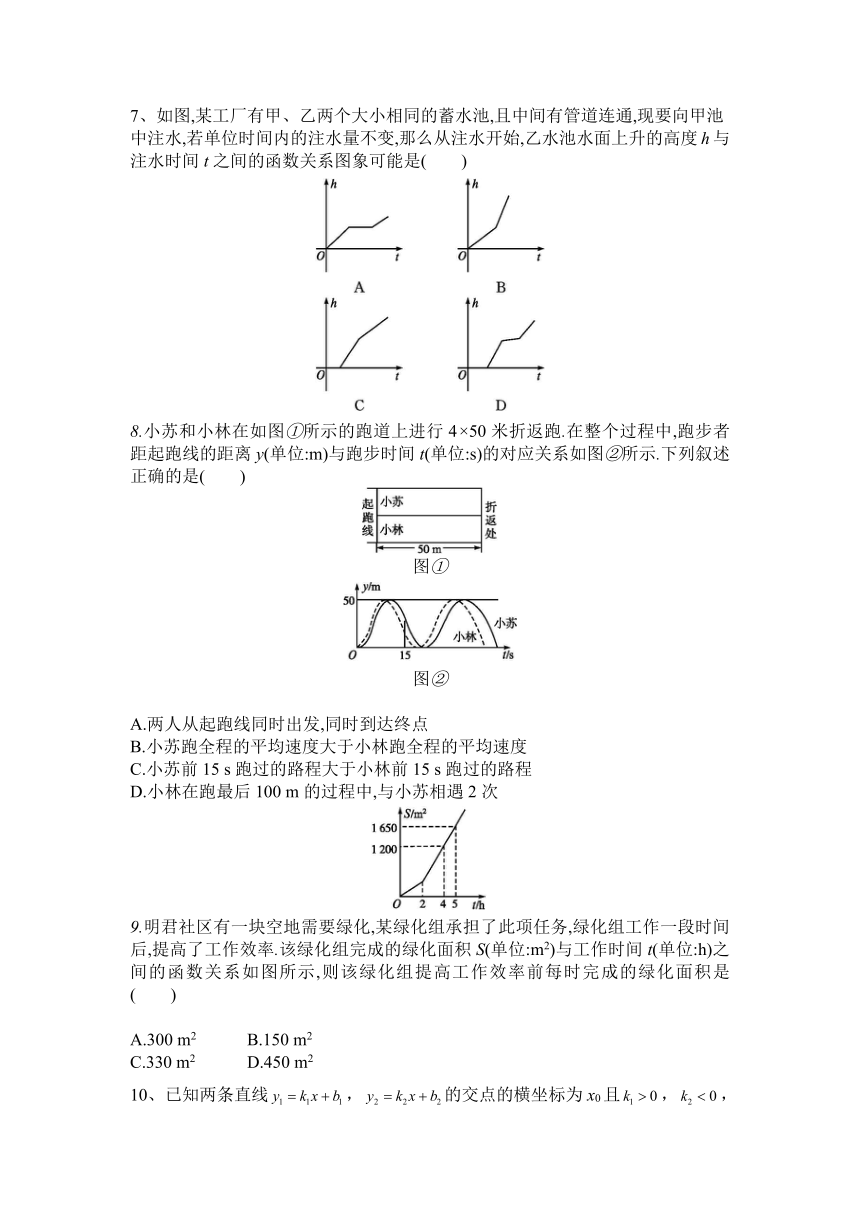
7、如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( )
8.小苏和小林在如图①所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如图②所示.下列叙述正确的是( )
图①
图②
A.两人从起跑线同时出发,同时到达终点
B.小苏跑全程的平均速度大于小林跑全程的平均速度
C.小苏前15
s跑过的路程大于小林前15
s跑过的路程
D.小林在跑最后100
m的过程中,与小苏相遇2次
9.明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每时完成的绿化面积是( )
A.300
m2
B.150
m2
C.330
m2
D.450
m2
10、已知两条直线,的交点的横坐标为x0且,,当时,则(
)
A.
B.
C.
D.
二、填空题
11、如果正比例函数的图象经过点,那么这个函数的表达式为
.
12.已知y与x成正比例,且时,,则y与x的函数关系式是
.
13.若直线,经过点,则_______.
14.已知一次函数,当时,,则当时,_______.
15.若一次函数的图象与y轴交于点A,则_____.
16.已知点A,B,C在同一条直线上,则______.
三、解答题
17、如图,
表示一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图象,两地间的距离是80千米,请根据图象回答下面问题:
(1)谁出发的较早?早多长时间?
(2)谁到达乙地较早?早到多长时间?
(3)途中,自行车和摩托车的速度各是多少?
(4)自行车出发几小时后被摩托车追上?此时摩托车出发几个小时?
18、某工厂有甲种原料130
kg,乙种原料144
kg.现用这两种原料生产出A,B两种产品共30件.已知生产每件A产品需甲种原料5
kg,乙种原料4
kg,且每件A产品可获利700元;生产每件B产品需甲种原料3
kg,乙种原料6
kg,且每件B产品可获利900元.设生产A产品x件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产A,B两种产品的方案有哪几种?
(2)设生产这30件产品可获利y元,写出y关于x的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
19、我国每年有大量土地被沙漠吞没,改造沙漠、保护土地资源已是一项十分紧迫的任务.某地现有耕地面积100万km2,沙漠面积为200万km2,土地沙漠化的变化情况如图所示,图中y表示新增沙漠面积(单位:万km2),x表示时间(单位:年).
(1)写出y与x之间的函数表达式.
(2)若不采取任何措施,10年后该地区将新增加沙漠面积多少?
(3)按此趋势继续下去,多少年后本地区将丧失全部的土地资源?
(4)如果从现在起开始采取植树造林等措施,每年可改造4万km2沙漠,那么到哪一年底,该地区沙漠面积将减少到176万km2?
20、如图所示,直线是一次函数在直角坐标系内的图象.
(1)观察图象,试求此一次函数的表达式;
(2)当时,其对应的y的值是多少?
(3)y的值随x值的增大怎样变化?
4.4一次函数的应用第1课时同步练习参考答案
一、选择题
1、某公司市场营销部的个人月收入与其每月的销售量成一次函数关系,
其图象如上图所示,由图中给出的信息可知,营销人员没有销售时(最低工资)的收入是(
B
)
A.310元
B.300元
C.290元
D.280元
2、已知一次函数y=kx-4(k<0)的图象与两坐标轴所围成的三角形的面积等于4,则该一次函数的表达式为( B )
A.y=-x-4
B.y=-2x-4
C.y=-3x+4
D.y=-3x-4
3、小明和哥哥从家里出发去买书,从家出发走了20分钟到一个离家1
000
m的书店.小明买了书后随即按原路返回;哥哥看了20分钟书后,用15分钟返家.下面的图象表示哥哥离家时间与距离之间关系的是( D )
4、一次函数的图象经过点A和B两点,那么该函数的表达式是(
D
)
A.
B.
C.
D.
5.正比例函数的图象经过点,那么它一定经过的点是(
D
)
A.
B.
C.
D.
6、甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20
km.他们前进的路程为s(单位:km),甲出发后的时间为t(单位:h),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息,下列说法正确的是(C )
A.甲的速度是4
km/h
B.乙的速度是10
km/h
C.乙比甲晚出发1
h
D.甲比乙晚到B地3
h
7、如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( D )
8.小苏和小林在如图①所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如图②所示.下列叙述正确的是( D )
图①
图②
A.两人从起跑线同时出发,同时到达终点
B.小苏跑全程的平均速度大于小林跑全程的平均速度
C.小苏前15
s跑过的路程大于小林前15
s跑过的路程
D.小林在跑最后100
m的过程中,与小苏相遇2次
9.明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每时完成的绿化面积是( B )
A.300
m2
B.150
m2
C.330
m2
D.450
m2
10、已知两条直线,的交点的横坐标为x0且,,当时,则(
B
)
A.
B.
C.
D.
二、填空题
11、如果正比例函数的图象经过点,那么这个函数的表达式为
.
12.已知y与x成正比例,且时,,则y与x的函数关系式是
.
13.若直线,经过点,则_______.
14.已知一次函数,当时,,则当时,_______.
15.若一次函数的图象与y轴交于点A,则_____.
16.已知点A,B,C在同一条直线上,则______.
答案:11.y=2x
12.y=-2x
13.
14.4
15.
16.-2
三、解答题
17、如图,
表示一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图象,两地间的距离是80千米,请根据图象回答下面问题:
(1)谁出发的较早?早多长时间?
(2)谁到达乙地较早?早到多长时间?
(3)途中,自行车和摩托车的速度各是多少?
(4)自行车出发几小时后被摩托车追上?此时摩托车出发几个小时?
解:(1)骑自行车者出发较早,早3个小时.
(2)骑摩托车者到达乙地较早,早到3个小时.
(3)自行车每小时走10千米,摩托车每小时走40千米.
(4)自行车出发4小时后被摩托车追上,此时摩托车出发1小时.
18、某工厂有甲种原料130
kg,乙种原料144
kg.现用这两种原料生产出A,B两种产品共30件.已知生产每件A产品需甲种原料5
kg,乙种原料4
kg,且每件A产品可获利700元;生产每件B产品需甲种原料3
kg,乙种原料6
kg,且每件B产品可获利900元.设生产A产品x件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产A,B两种产品的方案有哪几种?
(2)设生产这30件产品可获利y元,写出y关于x的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
解
(1)由题意得,5x+3(30-x)≤130,解得x≤20;
4x+6(30-x)≤144,解得x≥18.
故18≤x≤20,
∵x是正整数,∴x=18,19,20.
共有三种方案:
方案一:A产品18件,B产品12件,
方案二:A产品19件,B产品11件,
方案三:A产品20件,B产品10件.
(2)根据题意得,y=700x+900(30-x)=-200x+27
000,∵-200<0,∴y随x的增大而减小,
∴x=18时,y有最大值,y最大=-200×18+27
000=23
400元.
答:利润最大的方案是方案一,A产品18件,B产品12件,最大利润为23
400元.
19、我国每年有大量土地被沙漠吞没,改造沙漠、保护土地资源已是一项十分紧迫的任务.某地现有耕地面积100万km2,沙漠面积为200万km2,土地沙漠化的变化情况如图所示,图中y表示新增沙漠面积(单位:万km2),x表示时间(单位:年).
(1)写出y与x之间的函数表达式.
(2)若不采取任何措施,10年后该地区将新增加沙漠面积多少?
(3)按此趋势继续下去,多少年后本地区将丧失全部的土地资源?
(4)如果从现在起开始采取植树造林等措施,每年可改造4万km2沙漠,那么到哪一年底,该地区沙漠面积将减少到176万km2?
解
(1)y=2x(x≥1).
(2)当x=10时,y=20(万km2),即10年后新增沙漠面积为20万km2.
(3)当y=100时,即100=2x,所以x=50,即按此趋势继续下去,50年后本地区将丧失全部的土地资源.
(4)(200-176)÷(4-2)=12(年),即到第12年底,该地区沙漠面积将减少到176万km2.
20、如图所示,直线是一次函数在直角坐标系内的图象.
(1)观察图象,试求此一次函数的表达式;
(2)当时,其对应的y的值是多少?
(3)y的值随x值的增大怎样变化?
解:(1)由图象知L过点(0,-2),(3,2)所以,解得
k=,所以此一次函数的表达式为y=x-2;(2)当x=20时,y=×20-2=;(3)在y=x-2中,k=>0,故y随x的增大而增大.
一、选择题
1、某公司市场营销部的个人月收入与其每月的销售量成一次函数关系,
其图象如上图所示,由图中给出的信息可知,营销人员没有销售时(最低工资)的收入是(
)
A.310元
B.300元
C.290元
D.280元
2、已知一次函数y=kx-4(k<0)的图象与两坐标轴所围成的三角形的面积等于4,则该一次函数的表达式为( )
A.y=-x-4
B.y=-2x-4
C.y=-3x+4
D.y=-3x-4
3、小明和哥哥从家里出发去买书,从家出发走了20分钟到一个离家1
000
m的书店.小明买了书后随即按原路返回;哥哥看了20分钟书后,用15分钟返家.下面的图象表示哥哥离家时间与距离之间关系的是( )
4、一次函数的图象经过点A和B两点,那么该函数的表达式是(
)
A.
B.
C.
D.
5.正比例函数的图象经过点,那么它一定经过的点是(
)
A.
B.
C.
D.
6、甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20
km.他们前进的路程为s(单位:km),甲出发后的时间为t(单位:h),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息,下列说法正确的是( )
A.甲的速度是4
km/h
B.乙的速度是10
km/h
C.乙比甲晚出发1
h
D.甲比乙晚到B地3
h
7、如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( )
8.小苏和小林在如图①所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如图②所示.下列叙述正确的是( )
图①
图②
A.两人从起跑线同时出发,同时到达终点
B.小苏跑全程的平均速度大于小林跑全程的平均速度
C.小苏前15
s跑过的路程大于小林前15
s跑过的路程
D.小林在跑最后100
m的过程中,与小苏相遇2次
9.明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每时完成的绿化面积是( )
A.300
m2
B.150
m2
C.330
m2
D.450
m2
10、已知两条直线,的交点的横坐标为x0且,,当时,则(
)
A.
B.
C.
D.
二、填空题
11、如果正比例函数的图象经过点,那么这个函数的表达式为
.
12.已知y与x成正比例,且时,,则y与x的函数关系式是
.
13.若直线,经过点,则_______.
14.已知一次函数,当时,,则当时,_______.
15.若一次函数的图象与y轴交于点A,则_____.
16.已知点A,B,C在同一条直线上,则______.
三、解答题
17、如图,
表示一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图象,两地间的距离是80千米,请根据图象回答下面问题:
(1)谁出发的较早?早多长时间?
(2)谁到达乙地较早?早到多长时间?
(3)途中,自行车和摩托车的速度各是多少?
(4)自行车出发几小时后被摩托车追上?此时摩托车出发几个小时?
18、某工厂有甲种原料130
kg,乙种原料144
kg.现用这两种原料生产出A,B两种产品共30件.已知生产每件A产品需甲种原料5
kg,乙种原料4
kg,且每件A产品可获利700元;生产每件B产品需甲种原料3
kg,乙种原料6
kg,且每件B产品可获利900元.设生产A产品x件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产A,B两种产品的方案有哪几种?
(2)设生产这30件产品可获利y元,写出y关于x的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
19、我国每年有大量土地被沙漠吞没,改造沙漠、保护土地资源已是一项十分紧迫的任务.某地现有耕地面积100万km2,沙漠面积为200万km2,土地沙漠化的变化情况如图所示,图中y表示新增沙漠面积(单位:万km2),x表示时间(单位:年).
(1)写出y与x之间的函数表达式.
(2)若不采取任何措施,10年后该地区将新增加沙漠面积多少?
(3)按此趋势继续下去,多少年后本地区将丧失全部的土地资源?
(4)如果从现在起开始采取植树造林等措施,每年可改造4万km2沙漠,那么到哪一年底,该地区沙漠面积将减少到176万km2?
20、如图所示,直线是一次函数在直角坐标系内的图象.
(1)观察图象,试求此一次函数的表达式;
(2)当时,其对应的y的值是多少?
(3)y的值随x值的增大怎样变化?
4.4一次函数的应用第1课时同步练习参考答案
一、选择题
1、某公司市场营销部的个人月收入与其每月的销售量成一次函数关系,
其图象如上图所示,由图中给出的信息可知,营销人员没有销售时(最低工资)的收入是(
B
)
A.310元
B.300元
C.290元
D.280元
2、已知一次函数y=kx-4(k<0)的图象与两坐标轴所围成的三角形的面积等于4,则该一次函数的表达式为( B )
A.y=-x-4
B.y=-2x-4
C.y=-3x+4
D.y=-3x-4
3、小明和哥哥从家里出发去买书,从家出发走了20分钟到一个离家1
000
m的书店.小明买了书后随即按原路返回;哥哥看了20分钟书后,用15分钟返家.下面的图象表示哥哥离家时间与距离之间关系的是( D )
4、一次函数的图象经过点A和B两点,那么该函数的表达式是(
D
)
A.
B.
C.
D.
5.正比例函数的图象经过点,那么它一定经过的点是(
D
)
A.
B.
C.
D.
6、甲、乙两人沿相同的路线由A地到B地匀速前进,A,B两地间的路程为20
km.他们前进的路程为s(单位:km),甲出发后的时间为t(单位:h),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息,下列说法正确的是(C )
A.甲的速度是4
km/h
B.乙的速度是10
km/h
C.乙比甲晚出发1
h
D.甲比乙晚到B地3
h
7、如图,某工厂有甲、乙两个大小相同的蓄水池,且中间有管道连通,现要向甲池中注水,若单位时间内的注水量不变,那么从注水开始,乙水池水面上升的高度h与注水时间t之间的函数关系图象可能是( D )
8.小苏和小林在如图①所示的跑道上进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如图②所示.下列叙述正确的是( D )
图①
图②
A.两人从起跑线同时出发,同时到达终点
B.小苏跑全程的平均速度大于小林跑全程的平均速度
C.小苏前15
s跑过的路程大于小林前15
s跑过的路程
D.小林在跑最后100
m的过程中,与小苏相遇2次
9.明君社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率.该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每时完成的绿化面积是( B )
A.300
m2
B.150
m2
C.330
m2
D.450
m2
10、已知两条直线,的交点的横坐标为x0且,,当时,则(
B
)
A.
B.
C.
D.
二、填空题
11、如果正比例函数的图象经过点,那么这个函数的表达式为
.
12.已知y与x成正比例,且时,,则y与x的函数关系式是
.
13.若直线,经过点,则_______.
14.已知一次函数,当时,,则当时,_______.
15.若一次函数的图象与y轴交于点A,则_____.
16.已知点A,B,C在同一条直线上,则______.
答案:11.y=2x
12.y=-2x
13.
14.4
15.
16.-2
三、解答题
17、如图,
表示一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图象,两地间的距离是80千米,请根据图象回答下面问题:
(1)谁出发的较早?早多长时间?
(2)谁到达乙地较早?早到多长时间?
(3)途中,自行车和摩托车的速度各是多少?
(4)自行车出发几小时后被摩托车追上?此时摩托车出发几个小时?
解:(1)骑自行车者出发较早,早3个小时.
(2)骑摩托车者到达乙地较早,早到3个小时.
(3)自行车每小时走10千米,摩托车每小时走40千米.
(4)自行车出发4小时后被摩托车追上,此时摩托车出发1小时.
18、某工厂有甲种原料130
kg,乙种原料144
kg.现用这两种原料生产出A,B两种产品共30件.已知生产每件A产品需甲种原料5
kg,乙种原料4
kg,且每件A产品可获利700元;生产每件B产品需甲种原料3
kg,乙种原料6
kg,且每件B产品可获利900元.设生产A产品x件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产A,B两种产品的方案有哪几种?
(2)设生产这30件产品可获利y元,写出y关于x的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
解
(1)由题意得,5x+3(30-x)≤130,解得x≤20;
4x+6(30-x)≤144,解得x≥18.
故18≤x≤20,
∵x是正整数,∴x=18,19,20.
共有三种方案:
方案一:A产品18件,B产品12件,
方案二:A产品19件,B产品11件,
方案三:A产品20件,B产品10件.
(2)根据题意得,y=700x+900(30-x)=-200x+27
000,∵-200<0,∴y随x的增大而减小,
∴x=18时,y有最大值,y最大=-200×18+27
000=23
400元.
答:利润最大的方案是方案一,A产品18件,B产品12件,最大利润为23
400元.
19、我国每年有大量土地被沙漠吞没,改造沙漠、保护土地资源已是一项十分紧迫的任务.某地现有耕地面积100万km2,沙漠面积为200万km2,土地沙漠化的变化情况如图所示,图中y表示新增沙漠面积(单位:万km2),x表示时间(单位:年).
(1)写出y与x之间的函数表达式.
(2)若不采取任何措施,10年后该地区将新增加沙漠面积多少?
(3)按此趋势继续下去,多少年后本地区将丧失全部的土地资源?
(4)如果从现在起开始采取植树造林等措施,每年可改造4万km2沙漠,那么到哪一年底,该地区沙漠面积将减少到176万km2?
解
(1)y=2x(x≥1).
(2)当x=10时,y=20(万km2),即10年后新增沙漠面积为20万km2.
(3)当y=100时,即100=2x,所以x=50,即按此趋势继续下去,50年后本地区将丧失全部的土地资源.
(4)(200-176)÷(4-2)=12(年),即到第12年底,该地区沙漠面积将减少到176万km2.
20、如图所示,直线是一次函数在直角坐标系内的图象.
(1)观察图象,试求此一次函数的表达式;
(2)当时,其对应的y的值是多少?
(3)y的值随x值的增大怎样变化?
解:(1)由图象知L过点(0,-2),(3,2)所以,解得
k=,所以此一次函数的表达式为y=x-2;(2)当x=20时,y=×20-2=;(3)在y=x-2中,k=>0,故y随x的增大而增大.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
