沪科版八年级数学上册 13.1 三角形中的边角关系——边的关系课件(17张ppt)
文档属性
| 名称 | 沪科版八年级数学上册 13.1 三角形中的边角关系——边的关系课件(17张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-22 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
13.1
三角形中的边角关系
人教版高中数学必修二
——三角形中边的关系
[新课引入]
姚明腿长1.31米,有人说他一步能跨出3米。
你信吗?
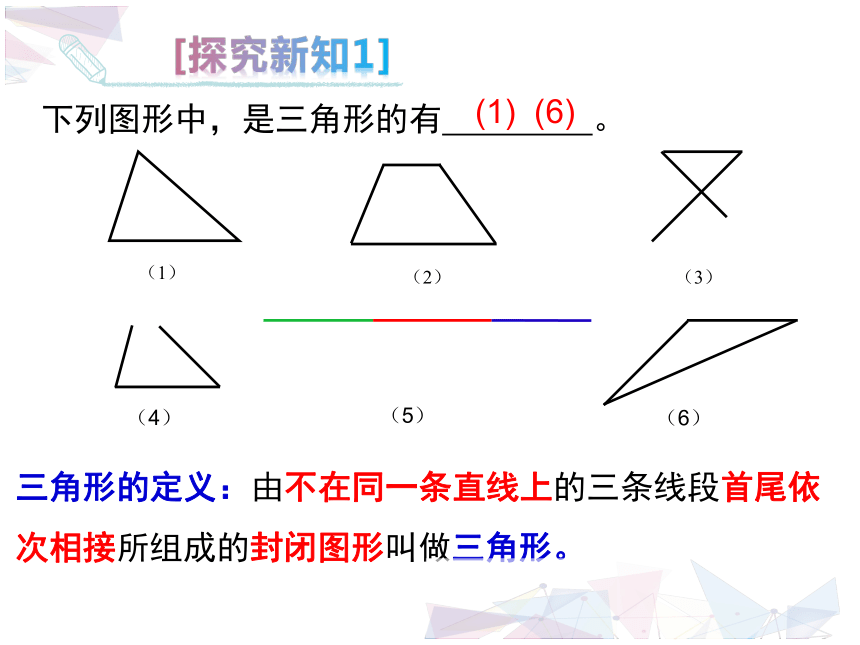
下列图形中,是三角形的有
。
(1)
(2)
(3)
(4)
(5)
(6)
(1)
(6)
三角形的定义:由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形叫做三角形。
[探究新知1]
A
B
C
b
c
a
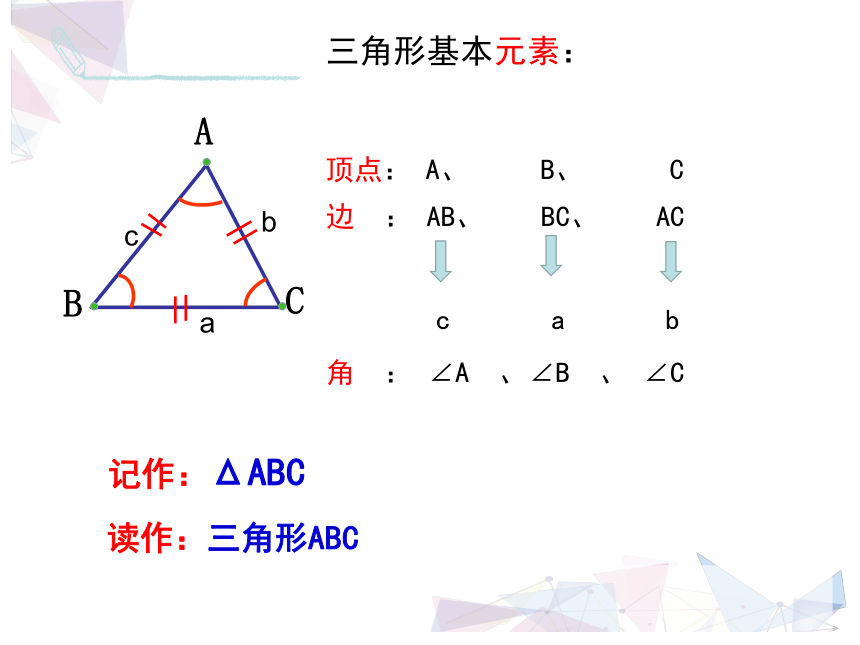
三角形基本元素:
顶点:
A、
B、
C
边
:
AB、
BC、
AC
c
a
b
角
:
∠A
、∠B
、
∠C
记作:ΔABC
读作:三角形ABC
导入新课
练一练
A
B
C
D
如图:图中共有
个三角形,分别是
;
以点B为顶点的三角形有______________;
以BC为边的三角形有_________________;
以∠C为内角的三角形有_______________。
3
?ABD
?ABD、?ABC
?ABC
?ABC、?ADC
、?ADC
、?ABC
导入新课
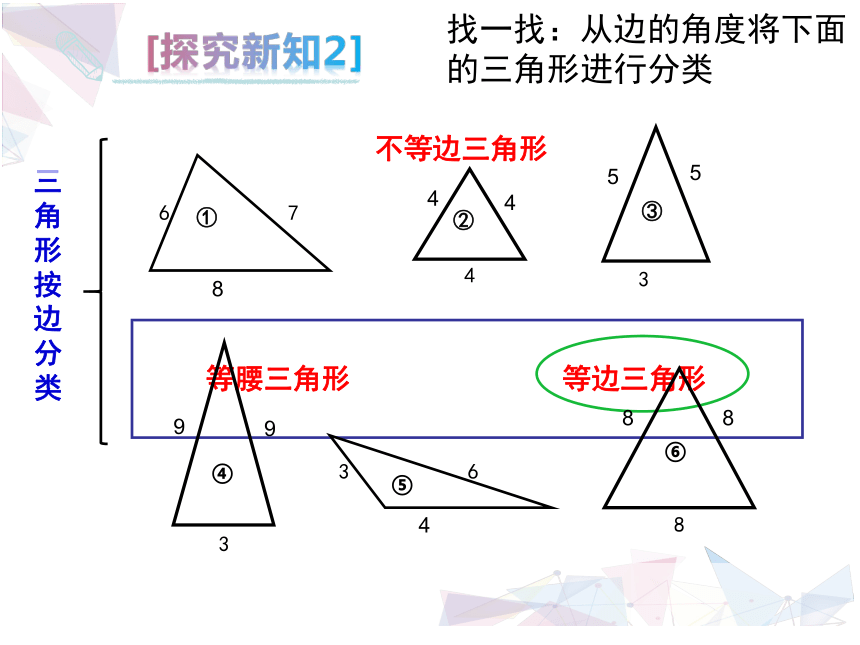
找一找:从边的角度将下面
的三角形进行分类
不等边三角形
等腰三角形
等边三角形
三角形按边分类
[探究新知2]
6
7
8
①
4
4
4
②
3
9
9
④
3
6
4
⑤
8
8
8
⑥
3
5
5
③
导入新课
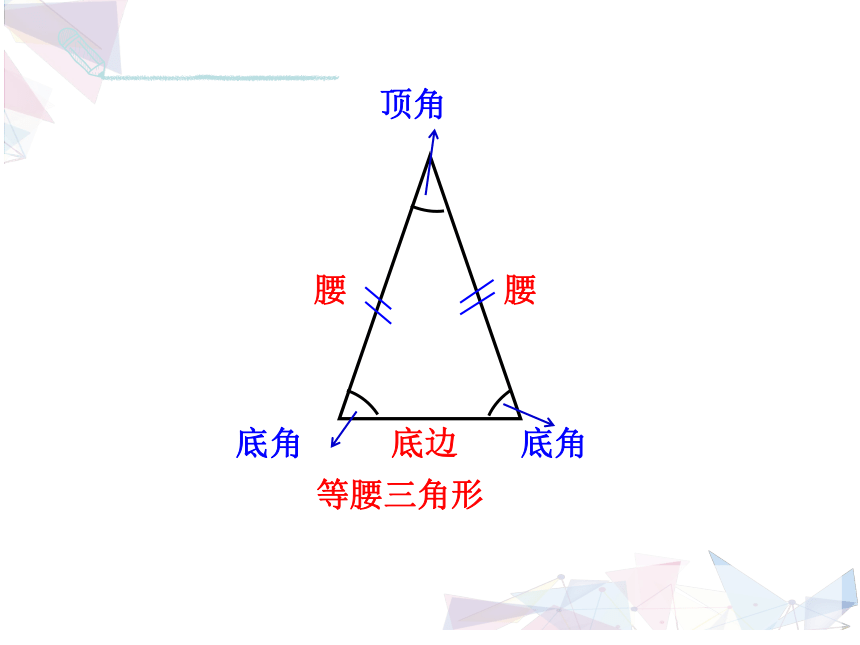
腰
腰
底边
顶角
底角
底角
等腰三角形
导入新课
人行横道
A
B
C
斜穿马路!
10m
24m
26m
因为10+24>26
[探究新知3]
想一想:这种行为明明很危险,为什么还有些人要这样做呢?
走旁边两条路的和要比斜穿马路远,即AC+BC>AB
任意一个三角形都有这样的关系吗?
导入新课
A
B
C
依据:两点之间线段最短。
同理
AB+BC_____AC
BC+AC_____AB
结论:三角形中任何两边的和大于第三边
>
>
>
思考:如图,在?ABC中,
AB+AC
BC(用“>、<或=”填空)
导入新课
A
B
C
|BC-AC||AC-AB||BC-AB|不等式的基本性质
AB>BC-AC
AC>BC-AB
AB>AC-BC
BC>AC-AB
AC>AB-BC
BC>AB-AC
结论:三角形中任何两边的差小于第三边
AB+AC>BC
AB+BC>AC
BC+AC>AB
[解决问题]
姚明腿长1.31米,有人说他一步能跨出3米。
你信吗?
[运用新知]
1.下列长度的三条线段(单位:cm)能否组成三角形?为什么?
(1)
4,5,6
(
)
(2)
8,4,3
(
)
(3)
3,8,5
(
)
(4)
m2+1,m2+3,2m2+5
(
)
不能
能
不能
不能
判断三条线段能否组成三角形,是否一定要检验三条线段中任何两条的和都大于第三条?
思考:
技巧:
分析:(1)因为4+5>6,4+6>5,5+6>4,所以能组成三角形
发现:要使上面三个不等式都成立,只需4+5>6这个不等式成立即可。为什么?
只需比较较小的两边之和是否大于第三边即可。
导入新课
解:设第三边长为Xcm,则:
3+X>5
解得:2。
∵
X为奇数
∴
X=3、5、7
答:第三边长为3cm或5cm或7cm。
方法提炼:已知三角形两边长,求出第三边长的取值范围。
5-33+5>X
,
[运用新知]
2.已知一个三角形的两边长分别为3cm和5cm,且第三边长为奇数,求第三边长?
两边之差<第三边<两边之和
导入新课
例:等腰三角形中周长为18cm,如果一边长为4cm,求另两边的长。
解:
①若底边长为4cm,设腰长为Xcm,则有
2X+4=18
,
X=7
②若腰长为4cm,设底边长为Xcm,则有
2×4+X=18
,
X=10
因为:4+4<10,所以4cm为腰长不能构成三角形
所以,三角形的另两边长都是7cm.
解得
解得
[巩固新知]
这节课你学习了哪些知识,
有哪些收获?
三角形
定义及其基本元素
边、顶点、角
按边分类
三边关系
任何两边之和大于第三边
任何两边之差小于第三边
不等边三角形
等腰三角形(包括等边三角形)
思想方法:分类讨论
方程思想
[课堂小结]
导入新课
选做题:思考三角形的中的角有哪些关系?如何得到?
[布置作业]
拓展题:如图,已知点D是?ABC内一点,试说明AB+AC>BD+CD.
必做题:同步练习
A
B
C
D
谢
谢
聆
听
人教版高中数学必修二
13.1
三角形中的边角关系
人教版高中数学必修二
——三角形中边的关系
[新课引入]
姚明腿长1.31米,有人说他一步能跨出3米。
你信吗?
下列图形中,是三角形的有
。
(1)
(2)
(3)
(4)
(5)
(6)
(1)
(6)
三角形的定义:由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形叫做三角形。
[探究新知1]
A
B
C
b
c
a
三角形基本元素:
顶点:
A、
B、
C
边
:
AB、
BC、
AC
c
a
b
角
:
∠A
、∠B
、
∠C
记作:ΔABC
读作:三角形ABC
导入新课
练一练
A
B
C
D
如图:图中共有
个三角形,分别是
;
以点B为顶点的三角形有______________;
以BC为边的三角形有_________________;
以∠C为内角的三角形有_______________。
3
?ABD
?ABD、?ABC
?ABC
?ABC、?ADC
、?ADC
、?ABC
导入新课
找一找:从边的角度将下面
的三角形进行分类
不等边三角形
等腰三角形
等边三角形
三角形按边分类
[探究新知2]
6
7
8
①
4
4
4
②
3
9
9
④
3
6
4
⑤
8
8
8
⑥
3
5
5
③
导入新课
腰
腰
底边
顶角
底角
底角
等腰三角形
导入新课
人行横道
A
B
C
斜穿马路!
10m
24m
26m
因为10+24>26
[探究新知3]
想一想:这种行为明明很危险,为什么还有些人要这样做呢?
走旁边两条路的和要比斜穿马路远,即AC+BC>AB
任意一个三角形都有这样的关系吗?
导入新课
A
B
C
依据:两点之间线段最短。
同理
AB+BC_____AC
BC+AC_____AB
结论:三角形中任何两边的和大于第三边
>
>
>
思考:如图,在?ABC中,
AB+AC
BC(用“>、<或=”填空)
导入新课
A
B
C
|BC-AC|
AB>BC-AC
AC>BC-AB
AB>AC-BC
BC>AC-AB
AC>AB-BC
BC>AB-AC
结论:三角形中任何两边的差小于第三边
AB+AC>BC
AB+BC>AC
BC+AC>AB
[解决问题]
姚明腿长1.31米,有人说他一步能跨出3米。
你信吗?
[运用新知]
1.下列长度的三条线段(单位:cm)能否组成三角形?为什么?
(1)
4,5,6
(
)
(2)
8,4,3
(
)
(3)
3,8,5
(
)
(4)
m2+1,m2+3,2m2+5
(
)
不能
能
不能
不能
判断三条线段能否组成三角形,是否一定要检验三条线段中任何两条的和都大于第三条?
思考:
技巧:
分析:(1)因为4+5>6,4+6>5,5+6>4,所以能组成三角形
发现:要使上面三个不等式都成立,只需4+5>6这个不等式成立即可。为什么?
只需比较较小的两边之和是否大于第三边即可。
导入新课
解:设第三边长为Xcm,则:
3+X>5
解得:2
∵
X为奇数
∴
X=3、5、7
答:第三边长为3cm或5cm或7cm。
方法提炼:已知三角形两边长,求出第三边长的取值范围。
5-3
,
[运用新知]
2.已知一个三角形的两边长分别为3cm和5cm,且第三边长为奇数,求第三边长?
两边之差<第三边<两边之和
导入新课
例:等腰三角形中周长为18cm,如果一边长为4cm,求另两边的长。
解:
①若底边长为4cm,设腰长为Xcm,则有
2X+4=18
,
X=7
②若腰长为4cm,设底边长为Xcm,则有
2×4+X=18
,
X=10
因为:4+4<10,所以4cm为腰长不能构成三角形
所以,三角形的另两边长都是7cm.
解得
解得
[巩固新知]
这节课你学习了哪些知识,
有哪些收获?
三角形
定义及其基本元素
边、顶点、角
按边分类
三边关系
任何两边之和大于第三边
任何两边之差小于第三边
不等边三角形
等腰三角形(包括等边三角形)
思想方法:分类讨论
方程思想
[课堂小结]
导入新课
选做题:思考三角形的中的角有哪些关系?如何得到?
[布置作业]
拓展题:如图,已知点D是?ABC内一点,试说明AB+AC>BD+CD.
必做题:同步练习
A
B
C
D
谢
谢
聆
听
人教版高中数学必修二
