沪科版九年级上册22.2相似三角形的判定课件(共13张PPT)
文档属性
| 名称 | 沪科版九年级上册22.2相似三角形的判定课件(共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 335.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-21 00:00:00 | ||
图片预览





文档简介
(共13张PPT)
22.2.2
相似三角形的判定(二)
学习目标
【学习目标】
1.经历三角形相似的判定定理1的探索及证明过程.
2.能应用定理1判定两个三角形相似,解决相关问题.
【学习重点】
三角形相似的判定定理1及应用.
【学习难点】
三角形相似的判定定理1的证明.
情景导入
旧知回顾:
1.全等三角形的判定方法有哪几种?
解:SSS、SAS、ASA、AAS、(HL)一共五种.
2.如何判定两个三角形相似?
解:需证明对应角相等,对应边成比例.
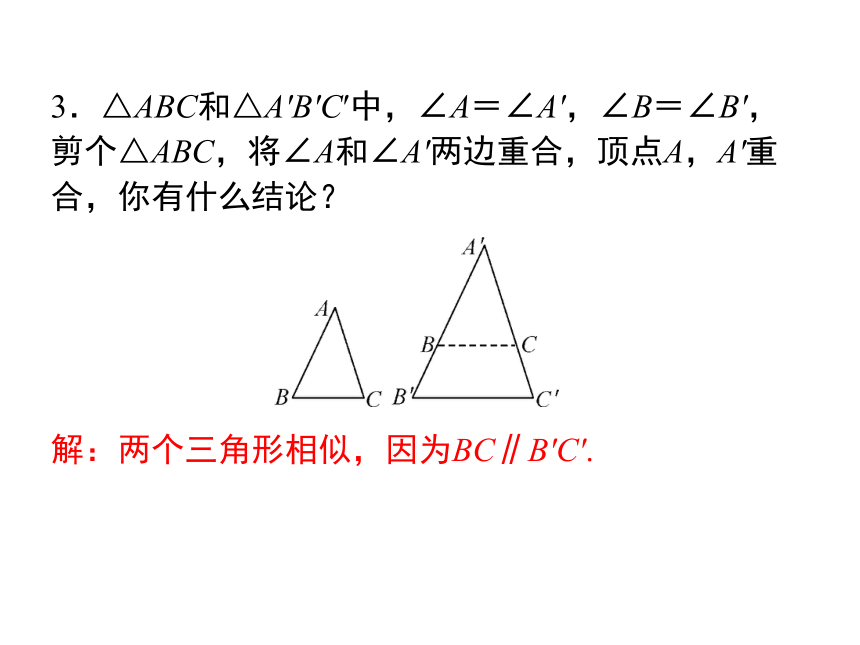
3.△ABC和△A′B′C′中,∠A=∠A′,∠B=∠B′,剪个△ABC,将∠A和∠A′两边重合,顶点A,A′重合,你有什么结论?
解:两个三角形相似,因为BC∥B′C′.
自学互研
知识模块一
相似三角形判定定理1的证明
相似三角形的判定定理1是什么?如何推导?
相似三角形判定定理1:如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似.(简称:两角分别相等的两个三角形相似).
探究:已知:如图在△A′B′C′和△ABC中,∠A′=∠A,∠B′=∠B.求证:△A′B′C′∽△ABC.
证明:在△ABC的AB上截BD=B′A′,
过D作DE∥AC,交BC于E.∴△ABC∽△DBE.
∵∠BDE=∠A,∠A=∠A′,∴∠BDE=∠A′.
∵∠B=∠B′,BD=B′A′,∴△DBE≌△B′A′C′.∴△ABC∽△A′B′C′.
范例
判断题
(1)有一个锐角对应相等的两个直角三角形相似.(
)
(2)所有的直角三角形都相似.( )
(3)有一个角相等的两个等腰三角形相似.(
)
(4)顶角相等的两个等腰三角形相似.(
)
√
×
×
√
知识模块二
相似三角形判定定理1的应用
范例
1.如图:点G在平行四边形ABCD的边DC的延长线上,AG交BC、BD于点E、F,则△AGD∽_________∽________.
△EGC
△EAB
2:已知:如图,AB⊥BD,ED⊥BD,垂足分别为点B、点D,C在线段BD上,AC⊥CE.求证:AB·DE=BC·CD.
【分析】欲证AB·DE=BC·CD,可证
=
,则证明△ABC∽△CDE即可,由题意可知∠1+∠2=90°,∠1+∠A=90°,则∠2=∠A.于是Rt△ABC∽Rt△CDE.
证明:∵AB⊥BD,ED⊥BD,AC⊥CE,∴∠B=∠D=90°,又∠1+∠A=90°,∠1+∠2=90°,∴∠A=∠2,∴△ABC∽△CDE,∴
=
,即AB·DE=BC·CD.
3:如图所示,在四边形ABCD中,AC平分∠DAB,∠ACD=∠ABC,求证:AC2=AB·AD.
证明:∵AC平分∠DAB,∴∠DAC=∠CAB,
又∵∠ACD=∠ABC,∴△ADC∽△ACB,
∴
=
,
∴AC2=AB·AD.
检测反馈
1.如图,在△ABC中,∠ACB=90°,DE⊥AB于点E,BD=10,AC=
BC,DE=
______.
2.如图,等边三角形ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,当∠APD=60°时,CD的长为__________.
(第1题图)
(第2题图)
6
3.如图,已知∠1=∠2=∠3,
求证:△ABC∽△ADE.
证明:∵∠1=∠2,∴∠1+∠DAC=∠3+∠DAC,即∠BAC=∠DAE.
∵∠2=∠3,∠AFE=∠DFC,
∴180°-∠2-∠DFC=180°-∠3-∠AFE,
即∠E=∠C,∴△ABC∽△ADE.
课堂小结
利用两角判定三角形相似
定理:两角分别相等的两个三角形相似
相似三角形的判定定理1的运用
22.2.2
相似三角形的判定(二)
学习目标
【学习目标】
1.经历三角形相似的判定定理1的探索及证明过程.
2.能应用定理1判定两个三角形相似,解决相关问题.
【学习重点】
三角形相似的判定定理1及应用.
【学习难点】
三角形相似的判定定理1的证明.
情景导入
旧知回顾:
1.全等三角形的判定方法有哪几种?
解:SSS、SAS、ASA、AAS、(HL)一共五种.
2.如何判定两个三角形相似?
解:需证明对应角相等,对应边成比例.
3.△ABC和△A′B′C′中,∠A=∠A′,∠B=∠B′,剪个△ABC,将∠A和∠A′两边重合,顶点A,A′重合,你有什么结论?
解:两个三角形相似,因为BC∥B′C′.
自学互研
知识模块一
相似三角形判定定理1的证明
相似三角形的判定定理1是什么?如何推导?
相似三角形判定定理1:如果一个三角形的两个角分别与另一个三角形的两个角对应相等,那么这两个三角形相似.(简称:两角分别相等的两个三角形相似).
探究:已知:如图在△A′B′C′和△ABC中,∠A′=∠A,∠B′=∠B.求证:△A′B′C′∽△ABC.
证明:在△ABC的AB上截BD=B′A′,
过D作DE∥AC,交BC于E.∴△ABC∽△DBE.
∵∠BDE=∠A,∠A=∠A′,∴∠BDE=∠A′.
∵∠B=∠B′,BD=B′A′,∴△DBE≌△B′A′C′.∴△ABC∽△A′B′C′.
范例
判断题
(1)有一个锐角对应相等的两个直角三角形相似.(
)
(2)所有的直角三角形都相似.( )
(3)有一个角相等的两个等腰三角形相似.(
)
(4)顶角相等的两个等腰三角形相似.(
)
√
×
×
√
知识模块二
相似三角形判定定理1的应用
范例
1.如图:点G在平行四边形ABCD的边DC的延长线上,AG交BC、BD于点E、F,则△AGD∽_________∽________.
△EGC
△EAB
2:已知:如图,AB⊥BD,ED⊥BD,垂足分别为点B、点D,C在线段BD上,AC⊥CE.求证:AB·DE=BC·CD.
【分析】欲证AB·DE=BC·CD,可证
=
,则证明△ABC∽△CDE即可,由题意可知∠1+∠2=90°,∠1+∠A=90°,则∠2=∠A.于是Rt△ABC∽Rt△CDE.
证明:∵AB⊥BD,ED⊥BD,AC⊥CE,∴∠B=∠D=90°,又∠1+∠A=90°,∠1+∠2=90°,∴∠A=∠2,∴△ABC∽△CDE,∴
=
,即AB·DE=BC·CD.
3:如图所示,在四边形ABCD中,AC平分∠DAB,∠ACD=∠ABC,求证:AC2=AB·AD.
证明:∵AC平分∠DAB,∴∠DAC=∠CAB,
又∵∠ACD=∠ABC,∴△ADC∽△ACB,
∴
=
,
∴AC2=AB·AD.
检测反馈
1.如图,在△ABC中,∠ACB=90°,DE⊥AB于点E,BD=10,AC=
BC,DE=
______.
2.如图,等边三角形ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,当∠APD=60°时,CD的长为__________.
(第1题图)
(第2题图)
6
3.如图,已知∠1=∠2=∠3,
求证:△ABC∽△ADE.
证明:∵∠1=∠2,∴∠1+∠DAC=∠3+∠DAC,即∠BAC=∠DAE.
∵∠2=∠3,∠AFE=∠DFC,
∴180°-∠2-∠DFC=180°-∠3-∠AFE,
即∠E=∠C,∴△ABC∽△ADE.
课堂小结
利用两角判定三角形相似
定理:两角分别相等的两个三角形相似
相似三角形的判定定理1的运用
