人教版八年级上册数学13.1.1轴对称课件(共24张)
文档属性
| 名称 | 人教版八年级上册数学13.1.1轴对称课件(共24张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-22 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
“第十三章轴对称
”
13.1轴对称
激趣导入
观察总结
探究新知
课堂练习
课堂小结
学习目标
轴对称图形
轴对称
轴对称的性质
观察川剧脸谱,思考画法有何讲究?
问题引入
观察思考
观察思考
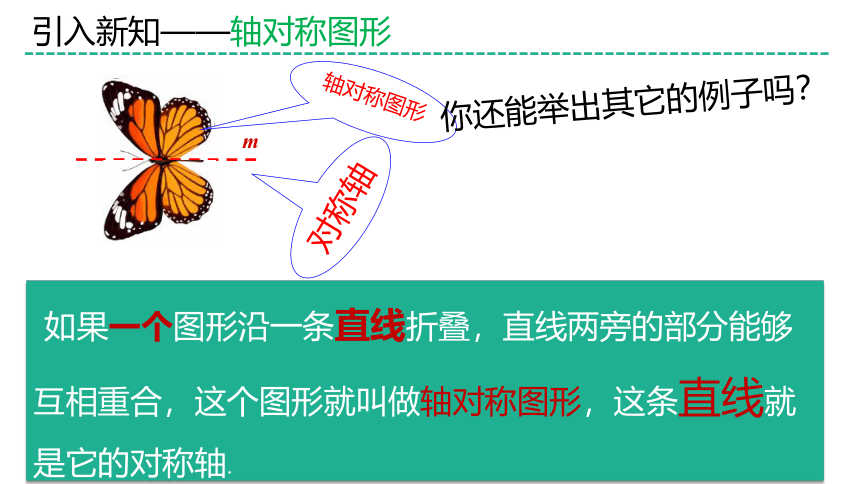
轴对称图形
对称轴
m
你还能举出其它的例子吗?
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
引入新知——轴对称图形
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
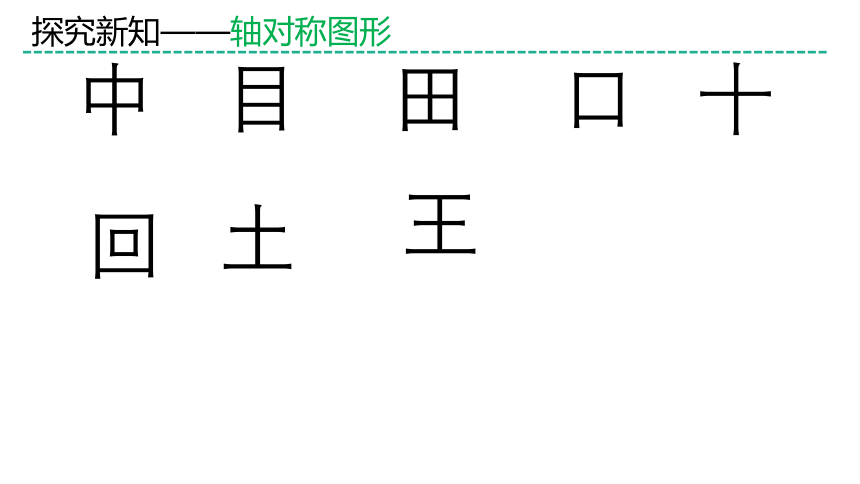
探究新知——轴对称图形
回
田
口
中
目
王
十
土
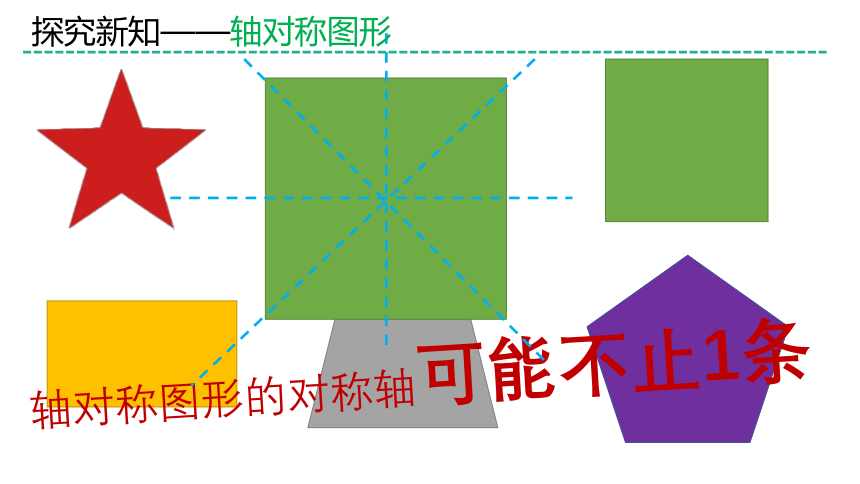
探究新知——轴对称图形
轴对称图形的对称轴可能不止1条
探究新知——轴对称图形
问题:观察下面每对图形(如图),你能类比前面的内容概括出它们的共同特征吗?
观察思考
A′
A
B
C
B′
C′
对称轴
折叠后重合的点是对应点,叫做对称点.如图点A、A
′就是一对对称点.
引入新知——成轴对称
如果一个图形沿一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线就是它的对称轴.
说一说:
轴对称图形
与两个图形成轴对称的异同比较
二者之间可以相互转化!
异同比较
轴对称图形
两个图形成轴对称
图形
区别
联系
1.一个图形具有的特殊形状
2.对称点在同一个图形上
3.一条或者多条
1.两个全等图形的特殊的位置关系
2.对称点分别在两个图形上
3.只有一条对称轴
1.都是沿着某条直线折叠后能重合.
2.可以互相转化.
归纳小结
如图,△ABC和△A′B′C′关于直线MN对称,点A′,B′,C′分别是点A,B,C的对称点,线段AA′,BB′,CC′与直线MN有什么关系?
A
B
C
A′
B′
C′
N
M
AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
观察思考
引入新知——垂直平分线
如图,MN⊥AA′,
AP=A′P.
直线MN是线段AA
′的垂直平分线.
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
引入新知——轴对称的性质
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
例1.下列表情图中,属于轴对称图形的是(
)
D
课堂练习
例2
做一做,找出下列各图形中的对称轴,并说明哪一个图形的对称轴最多.
课堂练习
例3:如图所示的每幅图形中的两个图案是轴对称的吗?如果是,指出它们的对称轴,
并找出一对对称点.
解:第(1)
(3)
是轴对称的
课堂练习
例4:如图,△ABC与△DEF关于直线MN对称,则以
下结论中错误的是( )
A.AB∥DF
B.∠B=∠E
C.AB=DE
D.AD的连线被MN垂直平分
A
课堂练习
1.想一想:一辆汽车的车牌在水中的倒影如图所示,你能确定该车的车牌号码吗?
巩固提高
2.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为( )
A.4cm2
B.8cm2
C.12cm2
D.16cm2
巩固提高
B
巩固提高
3.
如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB的度数为_______.
?
课堂总结
轴对称
轴对称
轴对称
图形
定义
性质
定义
性质
轴对称与
轴对称图形
联系
区别
线段的垂直平分线
“第十三章轴对称
”
13.1轴对称
激趣导入
观察总结
探究新知
课堂练习
课堂小结
学习目标
轴对称图形
轴对称
轴对称的性质
观察川剧脸谱,思考画法有何讲究?
问题引入
观察思考
观察思考
轴对称图形
对称轴
m
你还能举出其它的例子吗?
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
引入新知——轴对称图形
A
B
C
D
E
F
G
H
I
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z
探究新知——轴对称图形
回
田
口
中
目
王
十
土
探究新知——轴对称图形
轴对称图形的对称轴可能不止1条
探究新知——轴对称图形
问题:观察下面每对图形(如图),你能类比前面的内容概括出它们的共同特征吗?
观察思考
A′
A
B
C
B′
C′
对称轴
折叠后重合的点是对应点,叫做对称点.如图点A、A
′就是一对对称点.
引入新知——成轴对称
如果一个图形沿一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线就是它的对称轴.
说一说:
轴对称图形
与两个图形成轴对称的异同比较
二者之间可以相互转化!
异同比较
轴对称图形
两个图形成轴对称
图形
区别
联系
1.一个图形具有的特殊形状
2.对称点在同一个图形上
3.一条或者多条
1.两个全等图形的特殊的位置关系
2.对称点分别在两个图形上
3.只有一条对称轴
1.都是沿着某条直线折叠后能重合.
2.可以互相转化.
归纳小结
如图,△ABC和△A′B′C′关于直线MN对称,点A′,B′,C′分别是点A,B,C的对称点,线段AA′,BB′,CC′与直线MN有什么关系?
A
B
C
A′
B′
C′
N
M
AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
观察思考
引入新知——垂直平分线
如图,MN⊥AA′,
AP=A′P.
直线MN是线段AA
′的垂直平分线.
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线.
引入新知——轴对称的性质
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
例1.下列表情图中,属于轴对称图形的是(
)
D
课堂练习
例2
做一做,找出下列各图形中的对称轴,并说明哪一个图形的对称轴最多.
课堂练习
例3:如图所示的每幅图形中的两个图案是轴对称的吗?如果是,指出它们的对称轴,
并找出一对对称点.
解:第(1)
(3)
是轴对称的
课堂练习
例4:如图,△ABC与△DEF关于直线MN对称,则以
下结论中错误的是( )
A.AB∥DF
B.∠B=∠E
C.AB=DE
D.AD的连线被MN垂直平分
A
课堂练习
1.想一想:一辆汽车的车牌在水中的倒影如图所示,你能确定该车的车牌号码吗?
巩固提高
2.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为( )
A.4cm2
B.8cm2
C.12cm2
D.16cm2
巩固提高
B
巩固提高
3.
如图,Rt△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB的度数为_______.
?
课堂总结
轴对称
轴对称
轴对称
图形
定义
性质
定义
性质
轴对称与
轴对称图形
联系
区别
线段的垂直平分线
