沪科版九年级上册22.2.1 相似三角形的判定课件(18张)
文档属性
| 名称 | 沪科版九年级上册22.2.1 相似三角形的判定课件(18张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-22 12:07:38 | ||
图片预览





文档简介
(共18张PPT)
22.2.1
相似三角形的判定(一)
学习目标
【学习目标】
1.学会用平行于三角形一边的直线判定三角形相似.
2.经历定理的证明过程,培养分析问题、解决问题的能力.
【学习重点】
三角形相似的判定定理及应用.
【学习难点】
三角形相似的判定定理及应用.
情景导入
旧知回顾:
什么叫相似多边形?满足什么条件的两个三角形相似?
解:对应角相等,对应边的比相等,这两个多边形叫做相似多边形.对于△ABC和△A′B′C′,
当∠A=∠A′,∠B=∠B′,∠C=∠C′
且
=
=
,则△ABC∽△A′B′C′.
自学互研
知识模块一
相似三角形的基本概念
1.什么是相似三角形?它有何性质?
解:形状相同的两个三角形叫相似三角形.相似三角形对应角相等,对应边成比例.
2.△ABC与△A′B′C′相似比记为k1,△A′B′C′与△ABC相似比记为k2,k1与k2有何关系?当k1=k2时,这两个三角形全等吗?
解:k1=
,当k1=k2=1时,两个三角形全等.
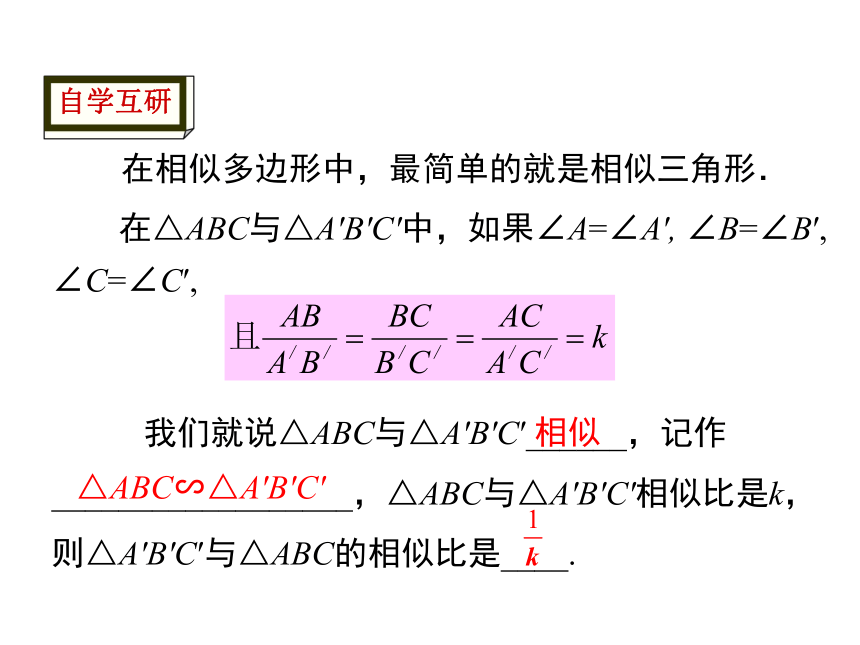
我们就说△ABC与△A′B′C′______,记作__________________,△ABC与△A′B′C′相似比是k,则△A′B′C′与△ABC的相似比是____.
在相似多边形中,最简单的就是相似三角形.
在△ABC与△A′B′C′中,如果∠A=∠A′,
∠B=∠B′,
∠C=∠C′,
△ABC∽△A′B′C′
相似
自学互研
反之如果△ABC∽△A′B′C′,则有∠A=_____,∠B=_____,∠C=____,
且
∠A′
∠B′
∠C′
自学互研
当相似比等于1时,相似图形是全等图形,全等是一种特殊的相似.
自学互研
如图所示,若△ABC∽△ADE,且∠ADE=∠B,则下列比例式正确的是( )
自学互研
范例
A.
=
B.
=
C.
=
D.
=
D
解:由对应关系可知D正确.
仿例
已知有两个三角形相似,一个边长分别为2,3,4,另一个对应边长分别为x,y,12,则x,y的值分别为_________________________.
6,9或8,16或18,24
解:分三类情况:
=
=
或
=
=
或
=
=
,可得x、y的值分别为6,9或8,16或18,24.
知识模块二
用平行于三角形一边的直线判定三角形相似
在△在ABC中,D为AB上任意一点,过D作BC的平行线DE,交AC于点E,那么△ADE与△ABC相似吗?
【分析】要判定两个三角形相似,我们可以从相似的定义来判定,即对应边成比例、对应角相等.
解:过D作AC的平行线交BC于F点.∵DE∥BC,DF∥AC,
∴
=
,
=
.
∵四边形DFCE是平行四边形
∴DE=FC,即
=
.∴
=
=
,
又∵∠A=∠A,∠B=∠ADE,∠C=∠AED,∴△ADE∽△ABC.
归纳
平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似.
范例
1:如图,在△ABC中,DE∥BC,若
=
,DE=3cm,求BC的长.
解:∵AD∶DB=1∶3,
∴AD∶AB=1∶4.
∵DE∥BC,∴△ADE∽△ABC,∴AD∶AB=DE∶BC.
∵DE=3cm,∴BC=12cm.
2:如图所示,已知在?ABCD中,E为AB延长线上的一点,DE与BC相交于F,请找出图中各对相似三角形.
解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,∴△BEF∽△CDF,△BEF∽△AED.
∴△BEF∽△CDF∽△AED.
3:在△ABC中,DE∥BC,M为DE中点,CM交AB于N,若AD∶AB=2∶3,求ND∶BD.
解:∵DE∥BC,∴△ADE∽△ABC,
∴
=
=
.
∵M为DE的中点,
∴
=
,
∵DM∥BC,
∴△NDM∽△NBC,
∴
=
=
,∴ND∶DB=1∶2.
检测反馈
1.(2015·岳阳中考)如图所示,已知点E、F分别是△ABC的边AC,AB的中点,BE与CF相交于点G,FG=2,则CF的长是( )
A.4
B.4.5
C.5
D.6
D
2.如图,AB⊥AE,DC⊥AE,EF⊥AE,垂足分别为A、C、E,求证:
=
.
证明:∵AB⊥AE,DC⊥AE,EF⊥AE,∴AB∥CD∥EF,∴△ABD∽△FED,
∴
=
.
又
∵DC∥FE,
∴
=
.
∴
=
.
3.如图,DE∥BC,DF∥AC,AD=4cm,BD=8cm,DE=5cm,试求线段BF的长.
解:∵DE∥BC,∴
=
,∴
=
,
∴BC=15.
∵DE∥BC,DF∥EC,
∴四边形DECF是平行四边形,∴DE=FC=5,
∴BF=15-5=10cm.
课堂小结
2.当相似比等于1时,相似图形即是全等图形,全等是一种特殊的相似;
3.平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似.
1.相似三角形的对应边成比例,对应角相等,相似
比等于对应边的比;
22.2.1
相似三角形的判定(一)
学习目标
【学习目标】
1.学会用平行于三角形一边的直线判定三角形相似.
2.经历定理的证明过程,培养分析问题、解决问题的能力.
【学习重点】
三角形相似的判定定理及应用.
【学习难点】
三角形相似的判定定理及应用.
情景导入
旧知回顾:
什么叫相似多边形?满足什么条件的两个三角形相似?
解:对应角相等,对应边的比相等,这两个多边形叫做相似多边形.对于△ABC和△A′B′C′,
当∠A=∠A′,∠B=∠B′,∠C=∠C′
且
=
=
,则△ABC∽△A′B′C′.
自学互研
知识模块一
相似三角形的基本概念
1.什么是相似三角形?它有何性质?
解:形状相同的两个三角形叫相似三角形.相似三角形对应角相等,对应边成比例.
2.△ABC与△A′B′C′相似比记为k1,△A′B′C′与△ABC相似比记为k2,k1与k2有何关系?当k1=k2时,这两个三角形全等吗?
解:k1=
,当k1=k2=1时,两个三角形全等.
我们就说△ABC与△A′B′C′______,记作__________________,△ABC与△A′B′C′相似比是k,则△A′B′C′与△ABC的相似比是____.
在相似多边形中,最简单的就是相似三角形.
在△ABC与△A′B′C′中,如果∠A=∠A′,
∠B=∠B′,
∠C=∠C′,
△ABC∽△A′B′C′
相似
自学互研
反之如果△ABC∽△A′B′C′,则有∠A=_____,∠B=_____,∠C=____,
且
∠A′
∠B′
∠C′
自学互研
当相似比等于1时,相似图形是全等图形,全等是一种特殊的相似.
自学互研
如图所示,若△ABC∽△ADE,且∠ADE=∠B,则下列比例式正确的是( )
自学互研
范例
A.
=
B.
=
C.
=
D.
=
D
解:由对应关系可知D正确.
仿例
已知有两个三角形相似,一个边长分别为2,3,4,另一个对应边长分别为x,y,12,则x,y的值分别为_________________________.
6,9或8,16或18,24
解:分三类情况:
=
=
或
=
=
或
=
=
,可得x、y的值分别为6,9或8,16或18,24.
知识模块二
用平行于三角形一边的直线判定三角形相似
在△在ABC中,D为AB上任意一点,过D作BC的平行线DE,交AC于点E,那么△ADE与△ABC相似吗?
【分析】要判定两个三角形相似,我们可以从相似的定义来判定,即对应边成比例、对应角相等.
解:过D作AC的平行线交BC于F点.∵DE∥BC,DF∥AC,
∴
=
,
=
.
∵四边形DFCE是平行四边形
∴DE=FC,即
=
.∴
=
=
,
又∵∠A=∠A,∠B=∠ADE,∠C=∠AED,∴△ADE∽△ABC.
归纳
平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似.
范例
1:如图,在△ABC中,DE∥BC,若
=
,DE=3cm,求BC的长.
解:∵AD∶DB=1∶3,
∴AD∶AB=1∶4.
∵DE∥BC,∴△ADE∽△ABC,∴AD∶AB=DE∶BC.
∵DE=3cm,∴BC=12cm.
2:如图所示,已知在?ABCD中,E为AB延长线上的一点,DE与BC相交于F,请找出图中各对相似三角形.
解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,∴△BEF∽△CDF,△BEF∽△AED.
∴△BEF∽△CDF∽△AED.
3:在△ABC中,DE∥BC,M为DE中点,CM交AB于N,若AD∶AB=2∶3,求ND∶BD.
解:∵DE∥BC,∴△ADE∽△ABC,
∴
=
=
.
∵M为DE的中点,
∴
=
,
∵DM∥BC,
∴△NDM∽△NBC,
∴
=
=
,∴ND∶DB=1∶2.
检测反馈
1.(2015·岳阳中考)如图所示,已知点E、F分别是△ABC的边AC,AB的中点,BE与CF相交于点G,FG=2,则CF的长是( )
A.4
B.4.5
C.5
D.6
D
2.如图,AB⊥AE,DC⊥AE,EF⊥AE,垂足分别为A、C、E,求证:
=
.
证明:∵AB⊥AE,DC⊥AE,EF⊥AE,∴AB∥CD∥EF,∴△ABD∽△FED,
∴
=
.
又
∵DC∥FE,
∴
=
.
∴
=
.
3.如图,DE∥BC,DF∥AC,AD=4cm,BD=8cm,DE=5cm,试求线段BF的长.
解:∵DE∥BC,∴
=
,∴
=
,
∴BC=15.
∵DE∥BC,DF∥EC,
∴四边形DECF是平行四边形,∴DE=FC=5,
∴BF=15-5=10cm.
课堂小结
2.当相似比等于1时,相似图形即是全等图形,全等是一种特殊的相似;
3.平行于三角形一边的直线与其他两边(或两边的延长线)相交,截得的三角形与原三角形相似.
1.相似三角形的对应边成比例,对应角相等,相似
比等于对应边的比;
