人教版八年级上册数学13.1.2线段的垂直平分线的性质课件(共24张PPT)
文档属性
| 名称 | 人教版八年级上册数学13.1.2线段的垂直平分线的性质课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 182.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-22 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
“第十三章轴对称
”
13.1.2线段的垂直平分线的性质
情境导入
探究新知
小试牛刀
巩固提高
课堂小结
学习目标
线段垂直平分线的性质
线段垂直平分线的判定
尺规作图
为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等?
(尺规作图)
A
B
C
问题引入
1.什么是轴对称图形?
2.
线段是轴对称图形吗?
3.
线段有几条对称轴?
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,
这个图形就叫做轴对称图形
是
两条
回顾旧知
动手操作,提出猜想
在线段的垂直平分线上任取一点,测量它到线段两端点的距离,
你发现了什么?再任取几点试试,并提出你的猜想。
线段垂直平分线上的点与这条线段两端点
的距离相等!
猜想?
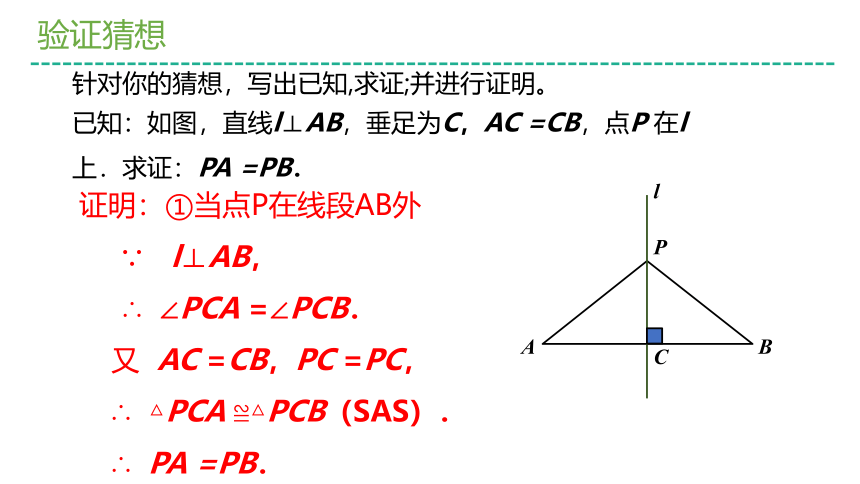
针对你的猜想,写出已知,求证;并进行证明。
已知:如图,直线l⊥AB,垂足为C,AC
=CB,点P
在l
上.求证:PA
=PB.
证明:①当点P在线段AB外
∵ l⊥AB,
∴
∠PCA
=∠PCB.
又
AC
=CB,PC
=PC,
∴
△PCA
≌△PCB(SAS).
∴
PA
=PB.
P
A
B
l
C
验证猜想
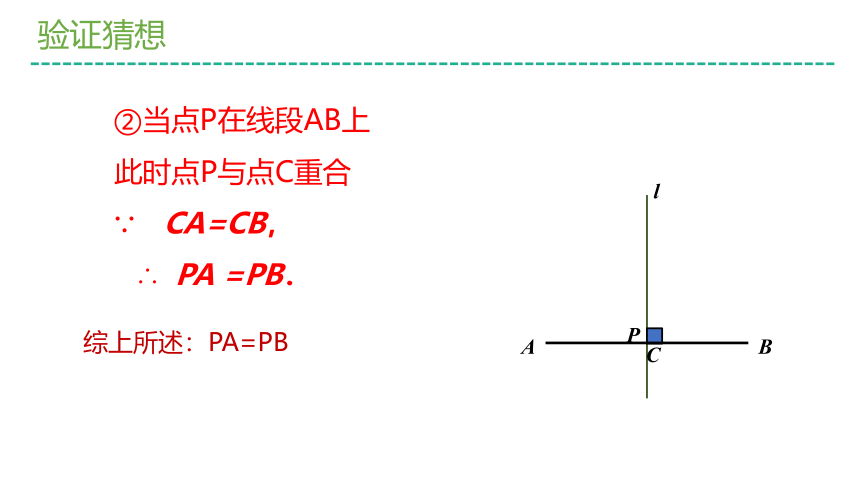
②当点P在线段AB上
此时点P与点C重合
∵ CA=CB,
∴
PA
=PB.
P
A
B
l
C
综上所述:PA=PB
验证猜想
线段垂直平分线的性质:
线段垂直平分线上的点和这条线段两个端点的距离相等.
引入新知
几何语言:
∵ 点P在线段AB
的垂直平分线上.
∴ PA=PB
反之是否成立?
P
A
B
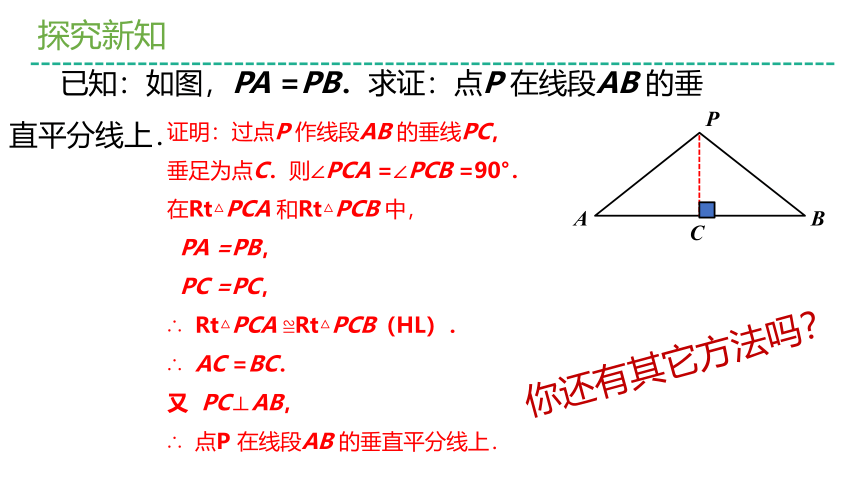
已知:如图,PA
=PB.求证:点P
在线段AB
的垂直平分线上.
证明:过点P
作线段AB
的垂线PC,
垂足为点C.则∠PCA
=∠PCB
=90°.
在Rt△PCA
和Rt△PCB
中,
PA
=PB,
PC
=PC,
∴
Rt△PCA
≌Rt△PCB(HL).
∴
AC
=BC.
又
PC⊥AB,
∴
点P
在线段AB
的垂直平分线上.
C
探究新知
你还有其它方法吗?
几何语言:
∵ PA
=PB,
∴ 点P
在AB
的垂直平分线上.
P
A
B
作用:判断一个点是否在线段的垂直平分线上.
线段垂直平分线的判定:
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
引入新知
1.说一说购物中心应该建于何处?
A
B
C
2.如何尺规作垂直平分线呢?
如何判断某一条直线是否为线段的垂直平分线?
几何语言:
∵ AB
=AC,MB
=MC,
∴ 直线AM
是线段BC
的垂直
平分线.
A
B
C
D
M
两点确定一条直线
对于如何尺规作线段的垂直平分线你是否有想法了呢?
验证猜想
A
B
C
D
作法:
(1)分别以点A,B为圆心,以大于
AB的长为半径作弧,两弧交于C,D两点.
(2)作直线CD.
CD即为所求.
探究新知
A
B
C
尺规作图确定购物中心的位置。
问题解决
尺规作图:经过已知直线外一点作这条直线的垂线.
A
B
C
D
E
K
已知:直线AB和AB外一点C
.
求作:AB的垂线,使它经过点C
.
作法:(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C
为圆心,CK长为半径作弧,交AB于点D和点E.
(4)作直线CF.
直线CF就是所求作的垂线.
(3)分别以点D和点E为圆心,大于
DE的长为半径作弧,两弧相交于点F.
F
探究新知
例1
如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,则BC的长为( )
A.5cm
B.10cm
C.15cm
D.17.5cm
C
课堂检验
例2
已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.求证:PA=PB=PC.
B
A
C
M
N
M'
N'
P
证明:
∵点P在线段AB的垂直平分线MN上,
∴PA=PB.
同理
PB=PC.
∴PA=PB=PC.
课堂检验
例3.下列说法:
①若点P、E是线段AB
的垂直平分线上两点,则EA=EB,
PA=PB;
②若PA=PB,EA=EB,则直线PE垂直平分线段AB;
③若PA=PB,则点P必是线段AB的垂直平分线上的点;
④若EA=EB,则经过点E
的直线垂直平分线段AB.
其中正确的有
(填序号).
①
②
③
课堂检验
例4.如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站.使两个小区到车站的路程一样长,该公共汽车站应建在什么地方?
A
B
公共汽车站
课堂检验
1.如图所示,AC=AD,BC=BD,则下列说法正确的是( )
A.AB垂直平分CD;
B
.CD垂直平分AB
;
C.AB与CD互相垂直平分;
D.CD平分∠
ACB
.
A
B
C
D
A
巩固提高
2.在锐角三角形ABC内一点P,,满足PA=PB=PC,则点P是△ABC
(
)
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
D
A
B
C
巩固提高
B
3.关于线段的垂直平分线有以下说法:
1)一条线段的垂直平分线的垂足,也是这条线段的中点
2)线段的垂直平分线是一条直线
3)一条线段的垂直平分线是这条线段的唯一对称轴
其中,正确的说法有(
)
A
1个
B
2个
C
3个
D
0个
巩固提高
4.如图所示,在△ABC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,试说明AD与EF的关系.
解:AD垂直平分EF.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴∠EAD=∠FAD,∠AED=∠AFD=90°.
又∵AD=AD,
∴△ADE≌△ADF,
∴AE=AF,DE=DF.
∴A、D均在线段EF的垂直平分线上,即直线AD垂直平分线段EF.
A
B
C
D
E
F
巩固提高
课堂小结
线段的垂直平分的性质和判定
性质
到线段的两个端点距离相等的点在线段的垂直平分线上
内容
判定
内容
作用
线段的垂直平分线上的点到线段的两个端点的距离相等
作用
见垂直平分线,得线段相等
判断一个点是否在线段的垂直平分线上
尺规作图
线段的垂直平分线
过直线外一点作已知直线的垂线
“第十三章轴对称
”
13.1.2线段的垂直平分线的性质
情境导入
探究新知
小试牛刀
巩固提高
课堂小结
学习目标
线段垂直平分线的性质
线段垂直平分线的判定
尺规作图
为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等?
(尺规作图)
A
B
C
问题引入
1.什么是轴对称图形?
2.
线段是轴对称图形吗?
3.
线段有几条对称轴?
如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,
这个图形就叫做轴对称图形
是
两条
回顾旧知
动手操作,提出猜想
在线段的垂直平分线上任取一点,测量它到线段两端点的距离,
你发现了什么?再任取几点试试,并提出你的猜想。
线段垂直平分线上的点与这条线段两端点
的距离相等!
猜想?
针对你的猜想,写出已知,求证;并进行证明。
已知:如图,直线l⊥AB,垂足为C,AC
=CB,点P
在l
上.求证:PA
=PB.
证明:①当点P在线段AB外
∵ l⊥AB,
∴
∠PCA
=∠PCB.
又
AC
=CB,PC
=PC,
∴
△PCA
≌△PCB(SAS).
∴
PA
=PB.
P
A
B
l
C
验证猜想
②当点P在线段AB上
此时点P与点C重合
∵ CA=CB,
∴
PA
=PB.
P
A
B
l
C
综上所述:PA=PB
验证猜想
线段垂直平分线的性质:
线段垂直平分线上的点和这条线段两个端点的距离相等.
引入新知
几何语言:
∵ 点P在线段AB
的垂直平分线上.
∴ PA=PB
反之是否成立?
P
A
B
已知:如图,PA
=PB.求证:点P
在线段AB
的垂直平分线上.
证明:过点P
作线段AB
的垂线PC,
垂足为点C.则∠PCA
=∠PCB
=90°.
在Rt△PCA
和Rt△PCB
中,
PA
=PB,
PC
=PC,
∴
Rt△PCA
≌Rt△PCB(HL).
∴
AC
=BC.
又
PC⊥AB,
∴
点P
在线段AB
的垂直平分线上.
C
探究新知
你还有其它方法吗?
几何语言:
∵ PA
=PB,
∴ 点P
在AB
的垂直平分线上.
P
A
B
作用:判断一个点是否在线段的垂直平分线上.
线段垂直平分线的判定:
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
引入新知
1.说一说购物中心应该建于何处?
A
B
C
2.如何尺规作垂直平分线呢?
如何判断某一条直线是否为线段的垂直平分线?
几何语言:
∵ AB
=AC,MB
=MC,
∴ 直线AM
是线段BC
的垂直
平分线.
A
B
C
D
M
两点确定一条直线
对于如何尺规作线段的垂直平分线你是否有想法了呢?
验证猜想
A
B
C
D
作法:
(1)分别以点A,B为圆心,以大于
AB的长为半径作弧,两弧交于C,D两点.
(2)作直线CD.
CD即为所求.
探究新知
A
B
C
尺规作图确定购物中心的位置。
问题解决
尺规作图:经过已知直线外一点作这条直线的垂线.
A
B
C
D
E
K
已知:直线AB和AB外一点C
.
求作:AB的垂线,使它经过点C
.
作法:(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C
为圆心,CK长为半径作弧,交AB于点D和点E.
(4)作直线CF.
直线CF就是所求作的垂线.
(3)分别以点D和点E为圆心,大于
DE的长为半径作弧,两弧相交于点F.
F
探究新知
例1
如图,在△ABC中,AB=AC=20cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为35cm,则BC的长为( )
A.5cm
B.10cm
C.15cm
D.17.5cm
C
课堂检验
例2
已知:如图,在ΔABC中,边AB,BC的垂直平分线交于P.求证:PA=PB=PC.
B
A
C
M
N
M'
N'
P
证明:
∵点P在线段AB的垂直平分线MN上,
∴PA=PB.
同理
PB=PC.
∴PA=PB=PC.
课堂检验
例3.下列说法:
①若点P、E是线段AB
的垂直平分线上两点,则EA=EB,
PA=PB;
②若PA=PB,EA=EB,则直线PE垂直平分线段AB;
③若PA=PB,则点P必是线段AB的垂直平分线上的点;
④若EA=EB,则经过点E
的直线垂直平分线段AB.
其中正确的有
(填序号).
①
②
③
课堂检验
例4.如图,A,B是路边两个新建小区,要在公路边增设一个公共汽车站.使两个小区到车站的路程一样长,该公共汽车站应建在什么地方?
A
B
公共汽车站
课堂检验
1.如图所示,AC=AD,BC=BD,则下列说法正确的是( )
A.AB垂直平分CD;
B
.CD垂直平分AB
;
C.AB与CD互相垂直平分;
D.CD平分∠
ACB
.
A
B
C
D
A
巩固提高
2.在锐角三角形ABC内一点P,,满足PA=PB=PC,则点P是△ABC
(
)
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
D
A
B
C
巩固提高
B
3.关于线段的垂直平分线有以下说法:
1)一条线段的垂直平分线的垂足,也是这条线段的中点
2)线段的垂直平分线是一条直线
3)一条线段的垂直平分线是这条线段的唯一对称轴
其中,正确的说法有(
)
A
1个
B
2个
C
3个
D
0个
巩固提高
4.如图所示,在△ABC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,试说明AD与EF的关系.
解:AD垂直平分EF.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴∠EAD=∠FAD,∠AED=∠AFD=90°.
又∵AD=AD,
∴△ADE≌△ADF,
∴AE=AF,DE=DF.
∴A、D均在线段EF的垂直平分线上,即直线AD垂直平分线段EF.
A
B
C
D
E
F
巩固提高
课堂小结
线段的垂直平分的性质和判定
性质
到线段的两个端点距离相等的点在线段的垂直平分线上
内容
判定
内容
作用
线段的垂直平分线上的点到线段的两个端点的距离相等
作用
见垂直平分线,得线段相等
判断一个点是否在线段的垂直平分线上
尺规作图
线段的垂直平分线
过直线外一点作已知直线的垂线
