粤教版(2019)高中物理 必修第二册 第2章 章末综合提升学案
文档属性
| 名称 | 粤教版(2019)高中物理 必修第二册 第2章 章末综合提升学案 |
|
|
| 格式 | doc | ||
| 文件大小 | 660.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-20 16:29:17 | ||
图片预览



文档简介
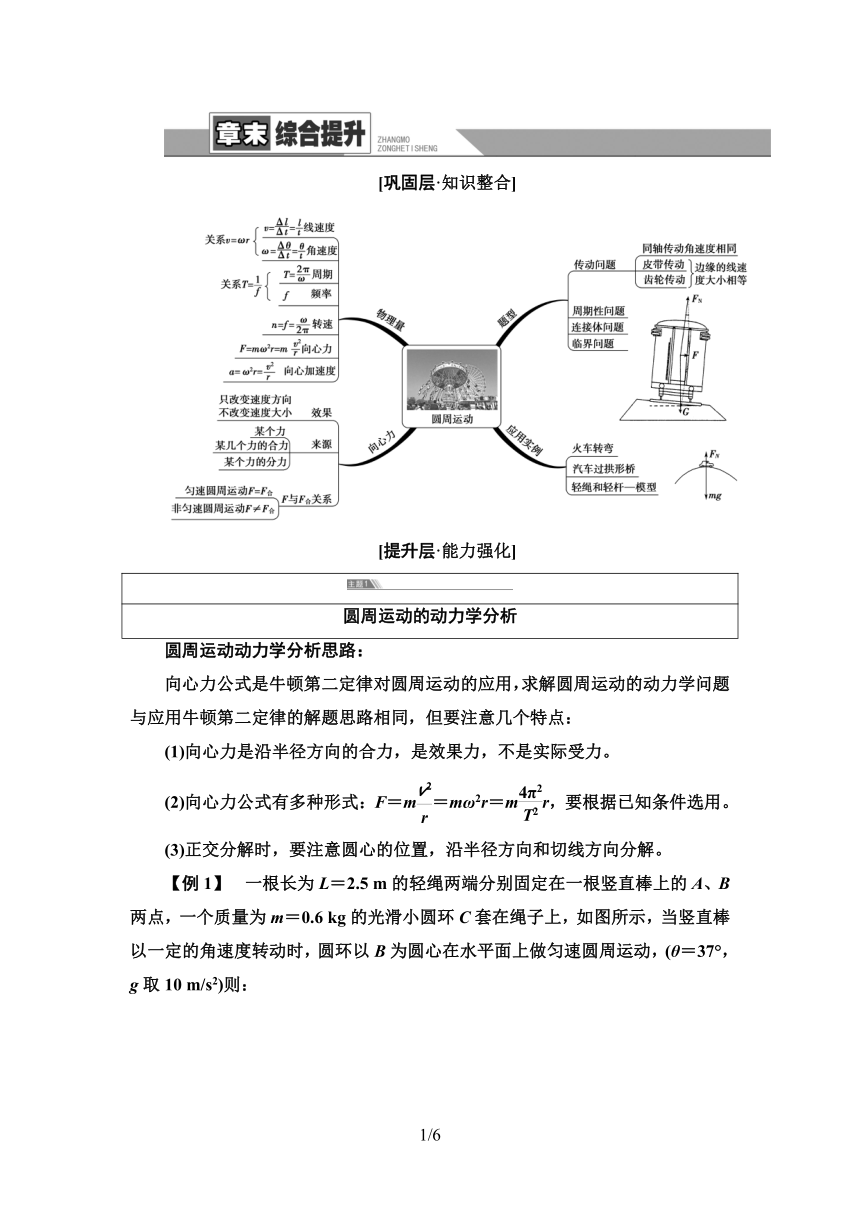
[巩固层·知识整合]
[提升层·能力强化]
圆周运动的动力学分析
圆周运动动力学分析思路:
向心力公式是牛顿第二定律对圆周运动的应用,求解圆周运动的动力学问题与应用牛顿第二定律的解题思路相同,但要注意几个特点:
(1)向心力是沿半径方向的合力,是效果力,不是实际受力。
(2)向心力公式有多种形式:F=m=mω2r=mr,要根据已知条件选用。
(3)正交分解时,要注意圆心的位置,沿半径方向和切线方向分解。
【例1】 一根长为L=2.5 m的轻绳两端分别固定在一根竖直棒上的A、B两点,一个质量为m=0.6 kg的光滑小圆环C套在绳子上,如图所示,当竖直棒以一定的角速度转动时,圆环以B为圆心在水平面上做匀速圆周运动,(θ=37°,g取10 m/s2)则:
(1)此时轻绳上的张力大小等于多少?
(2)竖直棒转动的角速度为多大?
思路点拨:小球受重力两个拉力做匀速圆周运动,合力提供向心力。
[解析] 对圆环受力分析如图
(1)圆环在竖直方向所受合外力为零,得:
Fsin θ=mg,所以F==10 N,即绳子拉力为10 N。
(2)圆环C在水平面内做匀速圆周运动,由于圆环光滑,所以圆环两端绳的拉力大小相等。BC段绳水平时,圆环C做圆周运动的半径r=BC,则有r+=L,解得r= m
则Fcos θ+F=mrω2
解得ω=3 rad/s。
[答案] (1)10 N (2)3 rad/s
[一语通关] 分析圆周运动问题的基本方法
1.首先要明确物体做圆周运动的轨道平面、圆心和半径。
2.其次,准确受力分析,弄清向心力的来源,不能漏力或添力(向心力)。
3.然后,由牛顿第二定律F=ma列方程,其中F是指向圆心方向的合外力,a是向心加速度,即或ω2r或用周期T来表示的形式。
圆周运动的临界和极值问题
临界极值问题的分类:
情境 小球在竖直面内做圆周运动恰好通过最高点 物体随圆盘一起做匀速圆周运动,刚好无相对滑动 绳子能够承受的最大拉力
模型 建构
分析 方法 假设法
图解法
【例2】 如图所示,AB为半径为R的光滑金属导轨(导轨厚度不计),a、b为分别沿导轨上、下两表面做圆周运动的小球(可看成质点),要使小球不脱离导轨,则a、b在导轨最高点的速度va、vb应满足什么条件?
思路点拨:小球刚好不致脱离轨道时,两球均由重力提供向心力。
[解析] 对a球在最高点,由牛顿第二定律得:
mag-Na=ma ①
要使a球不脱离轨道,
则Na>0 ②
由①②得:va<
对b球在最高点,由牛顿第二定律得:
mbg+Nb=mb ③
要使b球不脱离轨道,
则Nb>0 ④
由③④得:vb>。
[答案] va< vb>
[一语通关] 竖直平面内圆周运动的分析方法,竖直平面内的圆周运动一般是变速圆周运动,运动速度的大小和方向在不断发生变化,通常只研究物体在最高点和最低点的情况,而往往存在临界状态。
[培养层·素养升华]
水流星
夜空的流星,总是一划而过。“舞流星”是中国杂技的传统节目,常见的有《水流星》、《火流星》两种。《水流星》是在一根彩绳的两端,各系一只玻璃碗,内盛色水。演员甩绳舞弄,晶莹的玻璃碗飞快地旋转飞舞,即使碗底朝上,碗里的水也不会洒出来。
[设问探究]
1.假设“水流星”在竖直面内做圆周运动,该问题属于“绳模型”还是“杆模型”。
提示:绳模型。
2.当“水流星”在竖直面的最高点时,盛水的杯子杯口向下,水为什么也能不会洒出来。
提示:水受的合外力提供向心力,使水做圆周运动。
[深度思考]
1.(多选)杂技演员表演“水流星”,在长为0.9 m的细绳的一端,系一个与水的总质量为m=0.5 kg的盛水容器,以绳的另一端为圆心,在竖直平面内做圆周运动,如图所示,若“水流星”通过最高点时的速率为6 m/s,则下列说法正确的是(g取10 m/s2)( )
A.“水流星”通过最高点时,水不会从容器中流出
B.“水流星”通过最高点时,容器底部受到的压力为零
C.“水流星”通过最高点时,处于完全失重状态,不受重力的作用
D.“水流星”通过最高点时,绳子的拉力大小为15 N
AD [当水对容器底压力为零时有:mg=m,解得v===3 m/s,由于“水流星”通过最高点的速度为6 m/s,知水对容器底有压力,水不会从容器中流出,选项A正确,B错误;对水和容器分析,有:T+mg=m,解得T=15 N。知此时绳子的拉力为15 N,即在最高点时除受重力外还受绳的拉力,不是完全失重。故C错误,D正确;故选AD。]
2.如图所示,质量为0.5 kg的小杯里盛有1 kg的水,用绳子系住小杯在竖直平面内做“水流星”表演,转动半径为1 m,小杯通过最高点的速度为4 m/s,g取10 m/s2,求:
(1)在最高点时,绳的拉力;
(2)在最高点时水对小杯底的压力;
(3)为使“水流星”能完成竖直平面内的圆周运动,在最高点时最小速率是多少?
[解析] (1)以小杯m和水M为研究对象,根据牛顿第二定律:
T+(M+m)g=(M+m)
解得绳子的拉力:T=9 N,方向竖直向下。
(2)在最高点时,以水为研究对象:N+Mg=M
解得:N=6 N,根据牛顿第三定律,水对小杯底的压力为6 N,方向竖直向上。
(3)绳子拉力为0时,通过最高点速率最小:(M+m)g=(M+m)
解得:vmin=m/s。
[答案] (1)9 N,方向竖直向下 (2)6 N,方向竖直向上 (3) m/s
[素养点评]
对“水流星”这一杂技节目,为了说明杯子在最高点水不会流下来的原因。首先经过科学思维,抽象成物理模型——绳模型。通过对“水”做圆周运动的向心力分析,来解释这一现象。还可以对“水流星”整体分析绳子中的拉力情况。
5/252
[提升层·能力强化]
圆周运动的动力学分析
圆周运动动力学分析思路:
向心力公式是牛顿第二定律对圆周运动的应用,求解圆周运动的动力学问题与应用牛顿第二定律的解题思路相同,但要注意几个特点:
(1)向心力是沿半径方向的合力,是效果力,不是实际受力。
(2)向心力公式有多种形式:F=m=mω2r=mr,要根据已知条件选用。
(3)正交分解时,要注意圆心的位置,沿半径方向和切线方向分解。
【例1】 一根长为L=2.5 m的轻绳两端分别固定在一根竖直棒上的A、B两点,一个质量为m=0.6 kg的光滑小圆环C套在绳子上,如图所示,当竖直棒以一定的角速度转动时,圆环以B为圆心在水平面上做匀速圆周运动,(θ=37°,g取10 m/s2)则:
(1)此时轻绳上的张力大小等于多少?
(2)竖直棒转动的角速度为多大?
思路点拨:小球受重力两个拉力做匀速圆周运动,合力提供向心力。
[解析] 对圆环受力分析如图
(1)圆环在竖直方向所受合外力为零,得:
Fsin θ=mg,所以F==10 N,即绳子拉力为10 N。
(2)圆环C在水平面内做匀速圆周运动,由于圆环光滑,所以圆环两端绳的拉力大小相等。BC段绳水平时,圆环C做圆周运动的半径r=BC,则有r+=L,解得r= m
则Fcos θ+F=mrω2
解得ω=3 rad/s。
[答案] (1)10 N (2)3 rad/s
[一语通关] 分析圆周运动问题的基本方法
1.首先要明确物体做圆周运动的轨道平面、圆心和半径。
2.其次,准确受力分析,弄清向心力的来源,不能漏力或添力(向心力)。
3.然后,由牛顿第二定律F=ma列方程,其中F是指向圆心方向的合外力,a是向心加速度,即或ω2r或用周期T来表示的形式。
圆周运动的临界和极值问题
临界极值问题的分类:
情境 小球在竖直面内做圆周运动恰好通过最高点 物体随圆盘一起做匀速圆周运动,刚好无相对滑动 绳子能够承受的最大拉力
模型 建构
分析 方法 假设法
图解法
【例2】 如图所示,AB为半径为R的光滑金属导轨(导轨厚度不计),a、b为分别沿导轨上、下两表面做圆周运动的小球(可看成质点),要使小球不脱离导轨,则a、b在导轨最高点的速度va、vb应满足什么条件?
思路点拨:小球刚好不致脱离轨道时,两球均由重力提供向心力。
[解析] 对a球在最高点,由牛顿第二定律得:
mag-Na=ma ①
要使a球不脱离轨道,
则Na>0 ②
由①②得:va<
对b球在最高点,由牛顿第二定律得:
mbg+Nb=mb ③
要使b球不脱离轨道,
则Nb>0 ④
由③④得:vb>。
[答案] va< vb>
[一语通关] 竖直平面内圆周运动的分析方法,竖直平面内的圆周运动一般是变速圆周运动,运动速度的大小和方向在不断发生变化,通常只研究物体在最高点和最低点的情况,而往往存在临界状态。
[培养层·素养升华]
水流星
夜空的流星,总是一划而过。“舞流星”是中国杂技的传统节目,常见的有《水流星》、《火流星》两种。《水流星》是在一根彩绳的两端,各系一只玻璃碗,内盛色水。演员甩绳舞弄,晶莹的玻璃碗飞快地旋转飞舞,即使碗底朝上,碗里的水也不会洒出来。
[设问探究]
1.假设“水流星”在竖直面内做圆周运动,该问题属于“绳模型”还是“杆模型”。
提示:绳模型。
2.当“水流星”在竖直面的最高点时,盛水的杯子杯口向下,水为什么也能不会洒出来。
提示:水受的合外力提供向心力,使水做圆周运动。
[深度思考]
1.(多选)杂技演员表演“水流星”,在长为0.9 m的细绳的一端,系一个与水的总质量为m=0.5 kg的盛水容器,以绳的另一端为圆心,在竖直平面内做圆周运动,如图所示,若“水流星”通过最高点时的速率为6 m/s,则下列说法正确的是(g取10 m/s2)( )
A.“水流星”通过最高点时,水不会从容器中流出
B.“水流星”通过最高点时,容器底部受到的压力为零
C.“水流星”通过最高点时,处于完全失重状态,不受重力的作用
D.“水流星”通过最高点时,绳子的拉力大小为15 N
AD [当水对容器底压力为零时有:mg=m,解得v===3 m/s,由于“水流星”通过最高点的速度为6 m/s,知水对容器底有压力,水不会从容器中流出,选项A正确,B错误;对水和容器分析,有:T+mg=m,解得T=15 N。知此时绳子的拉力为15 N,即在最高点时除受重力外还受绳的拉力,不是完全失重。故C错误,D正确;故选AD。]
2.如图所示,质量为0.5 kg的小杯里盛有1 kg的水,用绳子系住小杯在竖直平面内做“水流星”表演,转动半径为1 m,小杯通过最高点的速度为4 m/s,g取10 m/s2,求:
(1)在最高点时,绳的拉力;
(2)在最高点时水对小杯底的压力;
(3)为使“水流星”能完成竖直平面内的圆周运动,在最高点时最小速率是多少?
[解析] (1)以小杯m和水M为研究对象,根据牛顿第二定律:
T+(M+m)g=(M+m)
解得绳子的拉力:T=9 N,方向竖直向下。
(2)在最高点时,以水为研究对象:N+Mg=M
解得:N=6 N,根据牛顿第三定律,水对小杯底的压力为6 N,方向竖直向上。
(3)绳子拉力为0时,通过最高点速率最小:(M+m)g=(M+m)
解得:vmin=m/s。
[答案] (1)9 N,方向竖直向下 (2)6 N,方向竖直向上 (3) m/s
[素养点评]
对“水流星”这一杂技节目,为了说明杯子在最高点水不会流下来的原因。首先经过科学思维,抽象成物理模型——绳模型。通过对“水”做圆周运动的向心力分析,来解释这一现象。还可以对“水流星”整体分析绳子中的拉力情况。
5/252
同课章节目录
- 第一章 抛体运动
- 第一节 曲线运动
- 第二节 运动的合成与分解
- 第三节 平抛运动
- 第四节 生活和生产中的抛体运动
- 第二章 圆周运动
- 第一节 匀速圆周运动
- 第二节 向心力与向心加速度
- 第三节 生活中的圆周运动
- 第四节 离心现象及其应用
- 第三章 万有引力定律
- 第一节 认识天体运动
- 第二节 认识万有引力定律
- 第三节 万有引力定律的应用
- 第四节 宇宙速度与航天
- 第四章 机械能及其守恒定律
- 第一节 功
- 第二节 功率
- 第三节 动能 动能定理
- 第四节 势能
- 第五节 机械能守恒定律
- 第六节 验证机械能守恒定律
- 第七节 生产和生活中的机械能守恒
- 第五章 牛顿力学的局限性与相对论初步
- 第一节 牛顿力学的成就与局限性
- 第二节 相对论时空观
- 第三节 宇宙起源和演化
