粤教版(2019)高中物理 必修第二册 第3章 章末综合提升学案
文档属性
| 名称 | 粤教版(2019)高中物理 必修第二册 第3章 章末综合提升学案 |
|
|
| 格式 | doc | ||
| 文件大小 | 911.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-20 00:00:00 | ||
图片预览





文档简介
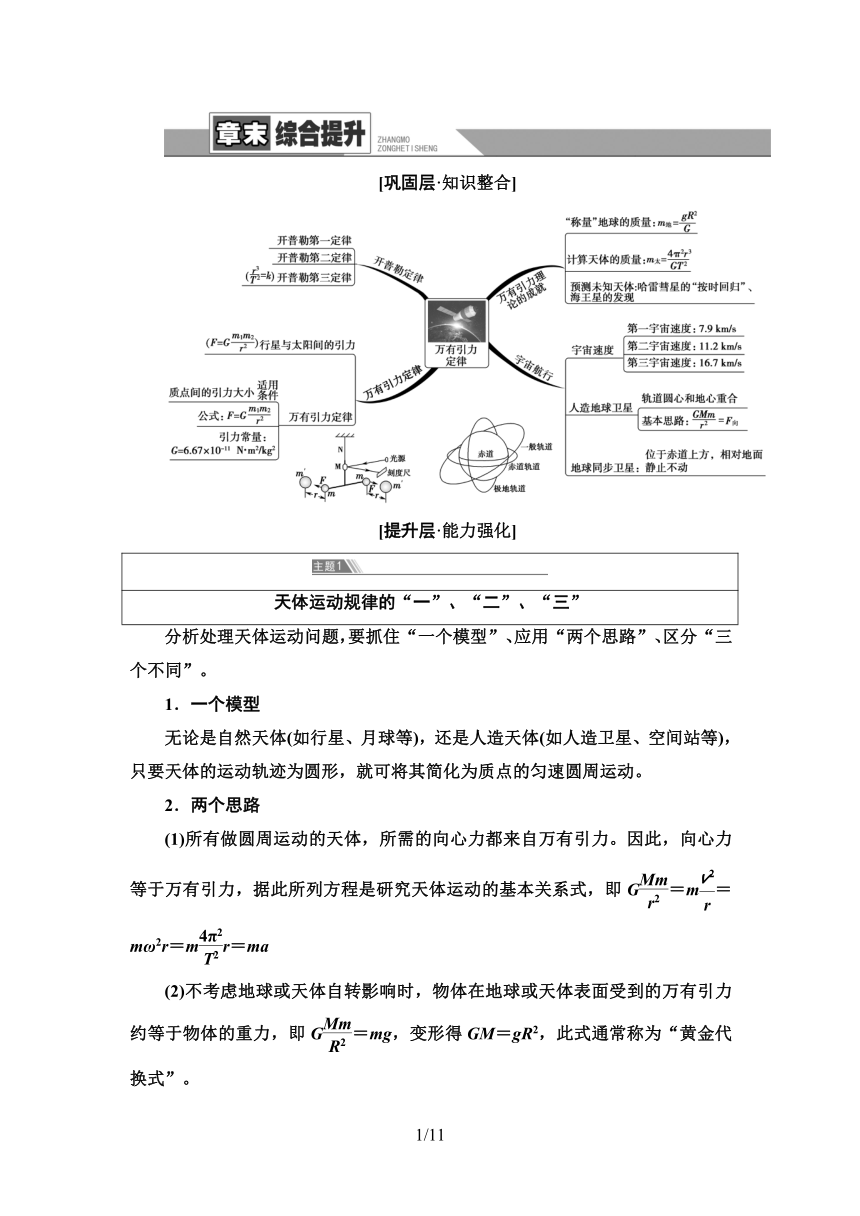
[巩固层·知识整合]
[提升层·能力强化]
天体运动规律的“一”、“二”、“三”
分析处理天体运动问题,要抓住“一个模型”、应用“两个思路”、区分“三个不同”。
1.一个模型
无论是自然天体(如行星、月球等),还是人造天体(如人造卫星、空间站等),只要天体的运动轨迹为圆形,就可将其简化为质点的匀速圆周运动。
2.两个思路
(1)所有做圆周运动的天体,所需的向心力都来自万有引力。因此,向心力等于万有引力,据此所列方程是研究天体运动的基本关系式,即G=m=mω2r=mr=ma
(2)不考虑地球或天体自转影响时,物体在地球或天体表面受到的万有引力约等于物体的重力,即G=mg,变形得GM=gR2,此式通常称为“黄金代换式”。
3.三个不同
(1)不同公式中r的含义不同。
在万有引力定律公式中,r的含义是两质点间的距离;在向心力公式(F=m=mω2r)中,r的含义是质点运动的轨道半径。
当一个天体绕另一个天体做匀速圆周运动时,两式中的r相等。
(2)运行速度、发射速度和宇宙速度的含义不同。
三种速度的比较,如下表所示
比较项 概念 大小 影响
因素
运行 速度 卫星绕中心天体做匀速圆周运动的速度 v= 轨道半径r越大,v越小
发射 速度 在地面上发射卫星的速度 大于或等于
7.9 km/s 卫星的发射高度越高,发射速度越大
宇宙 速度 实现某种效果所需的最小卫星发射速度 7.9 km/s
11.2 km/s
16.7 km/s 不同卫星发射要求不同
(3)卫星的向心加速度a、地球表面的重力加速度g、在地球表面的物体随地球自转做匀速圆周运动的向心加速度a′的含义不同。
①绕地球做匀速圆周运动的卫星的向心加速度a,由G=ma,得a=,其中r为卫星的轨道半径。
②若不考虑地球自转的影响,地球表面的重力加速度为g=,其中R为地球的半径。
③地球表面的物体随地球自转做匀速圆周运动的向心加速度a′=ω2Rcos θ,其中ω、R分别是地球的自转角速度和半径,θ是物体所在位置的纬度值。
【例1】 (多选)已知地球质量为M,半径为R,自转周期为T,地球同步卫星质量为m,引力常量为G,有关同步卫星,下列表述正确的是( )
A.卫星距地面的高度为
B.卫星的运行速度小于第一宇宙速度
C.卫星运行时受到的向心力大小为G
D.卫星运行的向心加速度小于地球表面的重力加速度
BD [对同步卫星由万有引力提供向心力G=m(R+h),所以h=-R,A错误;第一宇宙速度是最大的环绕速度,B正确;同步卫星运动的向心力等于万有引力,应为F=,C错误;同步卫星的向心加速度为a同=,地球表面的重力加速度a表=,知a表>a同,D正确。]
[一语通关] 解决天体运动的基本思路
解决天体运动问题的思路
1.将天体运动视为匀速圆周运动。
2.万有引力提供向心力,根据已知条件灵活选择合适的表达式,=m=mω2r=mr。
3.关于地球卫星的问题,有时还会应用GM=gR2做代换。
双星问题
1.双星
众多的天体中如果有两颗恒星,它们靠得较近,在万有引力作用下绕着它们连线上的某一点共同转动,这样的两颗恒星称为双星。
2.双星问题特点
如图所示为质量分别是m1和m2的两颗相距较近的恒星。它们间的距离为L。此双星问题的特点是:
(1)两星的运行轨道为同心圆,圆心是它们之间连线上的某一点;
(2)两星的向心力大小相等,由它们之间的万有引力提供;
(3)两星的运动周期、角速度相同;
(4)两星的运动半径之和等于它们之间的距离,即r1+r2=L。
3.双星问题的处理方法
双星间的万有引力提供了它们做圆周运动的向心力,即G=m1ω2r1=m2ω2r2,由此得出:
(1)m1r1=m2r2,即某恒星的运动半径与其质量成反比。
(2)由于ω=,r1+r2=L,所以两恒星的质量之和m1+m2=。
【例2】 宇宙中两颗相距较近的天体称为“双星”,它们以二者连线上的某一点为圆心做匀速圆周运动,而不会因万有引力的作用吸引到一起。
(1)试证明它们的轨道半径之比、线速度之比都等于质量的反比。
(2)设两者的质量分别为m1和m2,两者相距L,试写出它们角速度的表达式。
[解析] (1)证明:两天体绕同一点做匀速圆周运动的角速度ω一定相同。它们做匀速圆周运动的向心力由它们之间的万有引力提供,所以两天体与它们的圆心总是在一条直线上。
设两者的圆心为O点,轨道半径分别为R1和R2,如图所示。对两天体,由万有引力定律可分别列出
G=m1ω2R1 ①
G=m2ω2R2 ②
所以=,所以===,即它们的轨道半径、线速度之比都等于质量的反比。
(2)由①②两式相加得G=ω2(R1+R2) ③
因为R1+R2=L,所以ω=。
[答案] (1)见解析 (2)ω=
[一语通关] 双星问题的处理方法及两个结论
1.处理方法:双星间的万有引力提供了它们做圆周运动的向心力。即
G=m1ω2r1=m2ω2r2。
2.双星的两个结论
(1)运动半径:与质量成反比,即=。
(2)质量之和:m1+m2=。
1.如图所示,两颗星球组成的双星,在相互之间的万有引力作用下,绕连线上的O点做周期相同的匀速圆周运动。现测得两颗星之间的距离为L,质量之比为m1∶m2=3∶2,下列说法中正确的是( )
A.m1、m2做圆周运动的线速度之比为3∶2
B.m1、m2做圆周运动的角速度之比为3∶2
C.m1做圆周运动的半径为L
D.m2做圆周运动的半径为L
C [设双星m1、m2距转动中心O的距离分别为r1、r2,双星绕O点转动的角速度为ω,据万有引力定律和牛顿第二定律得
G=m1r1ω2=m2r2ω2,又r1+r2=L,m1∶m2=3∶2
所以可解得r1=L,r2=L
m1、m2做圆周运动的线速度分别为v1=r1ω,v2=r2ω,故v1∶v2=r1∶r2=2∶3。
综上所述,选项C正确。]
卫星(宇宙飞船)的变轨问题
1.卫星的变轨问题
卫星变轨时,先是线速度v发生变化导致需要的向心力发生变化,进而使轨道半径r发生变化。
(1)当卫星减速时,卫星所需的向心力F向=m减小,万 有引力大于所需的向心力,卫星将做近心运动,向低轨道变迁。
(2)当卫星加速时,卫星所需的向心力F向=m增大,万有引力不足以提供卫星所需的向心力,卫星将做离心运动,向高轨道变迁。
以上两点是比较椭圆和圆轨道切点速度的依据。
2.飞船对接问题
(1)低轨道飞船与高轨道空间站对接如图甲所示,低轨道飞船通过合理地加速,沿椭圆轨道(做离心运动)追上高轨道空间站与其完成对接。
甲 乙
(2)同一轨道飞船与空间站对接
如图乙所示,后面的飞船先减速降低高度,再加速提升高度,通过适当控制,使飞船追上空间站时恰好具有相同的速度。
3.卫星轨道的突变:由于技术上的需要,有时要在适当的位置短时间内启动飞行器上的发动机,使飞行器轨道发生突变,使其进入预定的轨道。如图所示,发射同步卫星时,可以分多过程完成:
(1)先将卫星发送到近地轨道Ⅰ。
(2)使其绕地球做匀速圆周运动,速率为v1,变轨时在P点点火加速,短时间内将速率由v1增加到v2,使卫星进入椭圆形的转移轨道Ⅱ。
(3)卫星运行到远地点Q时的速率为v3,此时进行第二次点火加速,在短时间内将速率由v3增加到v4,使卫星进入同步轨道Ⅲ,绕地球做匀速圆周运动。
【例3】 (多选)发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后点火,使其沿椭圆轨道2运动,最后再次点火,将卫星送入同步圆轨道3。轨道1、2相切于Q点,轨道2、3相切于P点,如图所示。当卫星分别在1、2、3轨道上正常运动时,以下说法正确的是( )
A.卫星在轨道3上的速率大于在轨道1上的速率
B.卫星在轨道3上的角速度小于在轨道1上的角速度
C.卫星在轨道1上经过Q点时的加速度大小大于它在轨道2上经过Q点时的加速度大小
D.卫星在轨道2上经过P点时的加速度大小等于它在轨道3上经过P点时的加速度大小
思路点拨:(1)不同的圆周运动轨道由v=、ω=比较速率、角速度大小。
(2)由a=比较卫星加速度大小。
BD [由G=m,得v=,因为r3>r1,所以v3<v1,A错误;由G=mrω2,得ω=,因为r3>r1,所以ω3<ω1,B正确;卫星在轨道1上经过Q点时的加速度为地球引力产生的,在轨道2上经过Q点时,也只有地球引力产生加速度,故两者大小应相等,C错误;同理,卫星在轨道2上经过P点时的加速度大小等于它在轨道3上经过P点时的加速度大小,D正确。]
[一语通关]
卫星变轨问题的分析技巧
1.根据引力与需要的向心力的关系分析
(1)当卫星绕天体做匀速圆周运动时,万有引力提供向心力,由G=m,得v=,由此可见轨道半径r越大,线速度v越小。
(2)当由于某原因速度v突然改变时,若速度v减小,则F>m,卫星将做近心运动,轨迹为椭圆;若速度v增大,则F<m,卫星将做离心运动,轨迹为椭圆,此时可用开普勒三定律分析其运动。
2.卫星到达椭圆轨道与圆轨道的切点时,卫星受到的万有引力相同,所以加速度相同。
2.宇宙飞船和空间站在同一轨道上运动,若飞船想与前面的空间站对接,飞船为了追上轨道空间站,可采取的方法是( )
A.飞船加速直到追上空间站,完成对接
B.飞船从原轨道减速至一个较低轨道,再加速追上空间站完成对接
C.飞船加速至一个较高轨道再减速追上空间站完成对接
D.无论飞船采取何种措施,均不能与空间站对接
B [由于宇宙飞船做圆周运动的向心力是地球对其施加的万有引力,由牛顿第二定律有=m,得v=,想追上同轨道上的空间站,直接加速会导致飞船轨道半径增大,由上式知飞船在一个新轨道上运行时速度比空间站的速度小,无法对接,故A错;飞船若先减速,它的轨道半径减小,但速度增大了,故在低轨道上飞船可接近或超过空间站,如图所示。当飞船运动到合适的位置后再加速,则其轨道半径增大,同时速度减小,当刚好运动到空间站所在轨道时停止加速,则飞船的速度刚好等于空间站的速度,可完成对接;若飞船先加速到一个较高轨道,其速度小于空间站速度,此时空间站比飞船运动快,当二者相对运动一周后,使飞船减速,轨道半径减小又使飞船速度增大,仍可追上空间站,但这种方法易造成飞船与空间站碰撞,不是最好的办法,且空间站追飞船不合题意,综上所述,方法应选B。]
[培养层·素养升华]
北斗卫星导航系统
中国北斗卫星导航系统(英文名称:BeiDou Navigation Satellite System,简称BDS)是中国自行研制的全球卫星导航系统,也是继GPS、GLONASS之后的第三个成熟的卫星导航系统。北斗卫星导航系统(BDS)和美国GPS、俄罗斯GLONASS、欧盟GALILEO,是联合国卫星导航委员会已认定的供应商。
北斗卫星导航系统由空间段、地面段和用户段三部分组成,可在全球范围内全天候、全天时为各类用户提供高精度、高可靠定位、导航、授时服务,并具短报文通信能力,已经初步具备区域导航、定位和授时能力,定位精度10米,测速精度0.2米/秒,授时精度10纳秒。
2020年7月31日上午,北斗三号全球卫星导航正式开通。
[设问探究]
1.北斗导航系统中有几颗地球同步卫星,而GPS导航系统由周期为12 h的卫星群组成,两者相比,谁的轨道半径大?谁的线速度大?
2.北斗导航系统中离地球越近的卫星所受的引力越大吗?
提示:1.由周期大的轨道半径大知,北斗导航同步卫星的轨道半径大,又由v=知GPS导航卫星的线速度大。
2.不一定,因卫星的质量不确定。
[深度思考]
1.北斗卫星导航系统(BDS)是我国自行研制的全球卫星导航系统,截止到2019年6月,我国已成功发射了46颗北斗导航卫星,并成功实现组网。其中A、B两颗北斗导航卫星绕地球做匀速圆周运动,SA、SB表示两卫星与地心的连线在单位时间内扫过的面积,vA、vB表示两卫星运行的速率。下列关系式正确的是( )
A.SA=SB B.=
C.= D.无法确定
B [卫星绕地球做匀速圆周运动,则有G=m=mr,由于S=,联立解得S=,由此可知,S与v成反比。选项B正确。]
2.北斗卫星导航系统是我国自行研制开发的区域性三维卫星定位与通信系统(CNSS),建立后的北斗卫星导航系统包括5颗同步卫星和30颗一般轨道卫星。关于这些卫星,以下说法正确的是( )
A.5颗同步卫星的轨道距地高度不同
B.5颗同步卫星的运行轨道不一定在同一平面内
C.导航系统所有卫星的运行速度一定大于第一宇宙速度
D.导航系统所有卫星中,运行轨道半径越大的,周期一定越大
D [因为同步卫星要和地球自转同步,所以运行轨道就在赤道所在平面内,根据F=G=mω2r因为ω一定,所以r必须固定,即一定位于空间同一轨道上且距地高度相同,故A、B错误;第一宇宙速度是近地卫星的环绕速度,也是最大的圆周运动的环绕速度。而同步卫星的轨道半径要大于近地卫星的轨道半径,所以它们运行的线速度一定小于7.9 km/s,故C错误;由公式G=mr得T=, 所以运行轨道半径越大的,周期一定越大,故D正确。故选D。]
[素养点评]
北斗卫星导航系统中有地球的同步卫星,也有非同步卫星,都在自己的轨道上运行,都满足万有引力提供向心力这个规律,能分析它们的周期、角速度、线速度、离地高度等物理量,体现了物理知识在生产生活中的重要性。在分析相关问题时,紧紧抓住F万=F向这个关系式,但是F向的具体表达式要依据分析的问题进行选择,做到具体问题具体分析。
10/10
[提升层·能力强化]
天体运动规律的“一”、“二”、“三”
分析处理天体运动问题,要抓住“一个模型”、应用“两个思路”、区分“三个不同”。
1.一个模型
无论是自然天体(如行星、月球等),还是人造天体(如人造卫星、空间站等),只要天体的运动轨迹为圆形,就可将其简化为质点的匀速圆周运动。
2.两个思路
(1)所有做圆周运动的天体,所需的向心力都来自万有引力。因此,向心力等于万有引力,据此所列方程是研究天体运动的基本关系式,即G=m=mω2r=mr=ma
(2)不考虑地球或天体自转影响时,物体在地球或天体表面受到的万有引力约等于物体的重力,即G=mg,变形得GM=gR2,此式通常称为“黄金代换式”。
3.三个不同
(1)不同公式中r的含义不同。
在万有引力定律公式中,r的含义是两质点间的距离;在向心力公式(F=m=mω2r)中,r的含义是质点运动的轨道半径。
当一个天体绕另一个天体做匀速圆周运动时,两式中的r相等。
(2)运行速度、发射速度和宇宙速度的含义不同。
三种速度的比较,如下表所示
比较项 概念 大小 影响
因素
运行 速度 卫星绕中心天体做匀速圆周运动的速度 v= 轨道半径r越大,v越小
发射 速度 在地面上发射卫星的速度 大于或等于
7.9 km/s 卫星的发射高度越高,发射速度越大
宇宙 速度 实现某种效果所需的最小卫星发射速度 7.9 km/s
11.2 km/s
16.7 km/s 不同卫星发射要求不同
(3)卫星的向心加速度a、地球表面的重力加速度g、在地球表面的物体随地球自转做匀速圆周运动的向心加速度a′的含义不同。
①绕地球做匀速圆周运动的卫星的向心加速度a,由G=ma,得a=,其中r为卫星的轨道半径。
②若不考虑地球自转的影响,地球表面的重力加速度为g=,其中R为地球的半径。
③地球表面的物体随地球自转做匀速圆周运动的向心加速度a′=ω2Rcos θ,其中ω、R分别是地球的自转角速度和半径,θ是物体所在位置的纬度值。
【例1】 (多选)已知地球质量为M,半径为R,自转周期为T,地球同步卫星质量为m,引力常量为G,有关同步卫星,下列表述正确的是( )
A.卫星距地面的高度为
B.卫星的运行速度小于第一宇宙速度
C.卫星运行时受到的向心力大小为G
D.卫星运行的向心加速度小于地球表面的重力加速度
BD [对同步卫星由万有引力提供向心力G=m(R+h),所以h=-R,A错误;第一宇宙速度是最大的环绕速度,B正确;同步卫星运动的向心力等于万有引力,应为F=,C错误;同步卫星的向心加速度为a同=,地球表面的重力加速度a表=,知a表>a同,D正确。]
[一语通关] 解决天体运动的基本思路
解决天体运动问题的思路
1.将天体运动视为匀速圆周运动。
2.万有引力提供向心力,根据已知条件灵活选择合适的表达式,=m=mω2r=mr。
3.关于地球卫星的问题,有时还会应用GM=gR2做代换。
双星问题
1.双星
众多的天体中如果有两颗恒星,它们靠得较近,在万有引力作用下绕着它们连线上的某一点共同转动,这样的两颗恒星称为双星。
2.双星问题特点
如图所示为质量分别是m1和m2的两颗相距较近的恒星。它们间的距离为L。此双星问题的特点是:
(1)两星的运行轨道为同心圆,圆心是它们之间连线上的某一点;
(2)两星的向心力大小相等,由它们之间的万有引力提供;
(3)两星的运动周期、角速度相同;
(4)两星的运动半径之和等于它们之间的距离,即r1+r2=L。
3.双星问题的处理方法
双星间的万有引力提供了它们做圆周运动的向心力,即G=m1ω2r1=m2ω2r2,由此得出:
(1)m1r1=m2r2,即某恒星的运动半径与其质量成反比。
(2)由于ω=,r1+r2=L,所以两恒星的质量之和m1+m2=。
【例2】 宇宙中两颗相距较近的天体称为“双星”,它们以二者连线上的某一点为圆心做匀速圆周运动,而不会因万有引力的作用吸引到一起。
(1)试证明它们的轨道半径之比、线速度之比都等于质量的反比。
(2)设两者的质量分别为m1和m2,两者相距L,试写出它们角速度的表达式。
[解析] (1)证明:两天体绕同一点做匀速圆周运动的角速度ω一定相同。它们做匀速圆周运动的向心力由它们之间的万有引力提供,所以两天体与它们的圆心总是在一条直线上。
设两者的圆心为O点,轨道半径分别为R1和R2,如图所示。对两天体,由万有引力定律可分别列出
G=m1ω2R1 ①
G=m2ω2R2 ②
所以=,所以===,即它们的轨道半径、线速度之比都等于质量的反比。
(2)由①②两式相加得G=ω2(R1+R2) ③
因为R1+R2=L,所以ω=。
[答案] (1)见解析 (2)ω=
[一语通关] 双星问题的处理方法及两个结论
1.处理方法:双星间的万有引力提供了它们做圆周运动的向心力。即
G=m1ω2r1=m2ω2r2。
2.双星的两个结论
(1)运动半径:与质量成反比,即=。
(2)质量之和:m1+m2=。
1.如图所示,两颗星球组成的双星,在相互之间的万有引力作用下,绕连线上的O点做周期相同的匀速圆周运动。现测得两颗星之间的距离为L,质量之比为m1∶m2=3∶2,下列说法中正确的是( )
A.m1、m2做圆周运动的线速度之比为3∶2
B.m1、m2做圆周运动的角速度之比为3∶2
C.m1做圆周运动的半径为L
D.m2做圆周运动的半径为L
C [设双星m1、m2距转动中心O的距离分别为r1、r2,双星绕O点转动的角速度为ω,据万有引力定律和牛顿第二定律得
G=m1r1ω2=m2r2ω2,又r1+r2=L,m1∶m2=3∶2
所以可解得r1=L,r2=L
m1、m2做圆周运动的线速度分别为v1=r1ω,v2=r2ω,故v1∶v2=r1∶r2=2∶3。
综上所述,选项C正确。]
卫星(宇宙飞船)的变轨问题
1.卫星的变轨问题
卫星变轨时,先是线速度v发生变化导致需要的向心力发生变化,进而使轨道半径r发生变化。
(1)当卫星减速时,卫星所需的向心力F向=m减小,万 有引力大于所需的向心力,卫星将做近心运动,向低轨道变迁。
(2)当卫星加速时,卫星所需的向心力F向=m增大,万有引力不足以提供卫星所需的向心力,卫星将做离心运动,向高轨道变迁。
以上两点是比较椭圆和圆轨道切点速度的依据。
2.飞船对接问题
(1)低轨道飞船与高轨道空间站对接如图甲所示,低轨道飞船通过合理地加速,沿椭圆轨道(做离心运动)追上高轨道空间站与其完成对接。
甲 乙
(2)同一轨道飞船与空间站对接
如图乙所示,后面的飞船先减速降低高度,再加速提升高度,通过适当控制,使飞船追上空间站时恰好具有相同的速度。
3.卫星轨道的突变:由于技术上的需要,有时要在适当的位置短时间内启动飞行器上的发动机,使飞行器轨道发生突变,使其进入预定的轨道。如图所示,发射同步卫星时,可以分多过程完成:
(1)先将卫星发送到近地轨道Ⅰ。
(2)使其绕地球做匀速圆周运动,速率为v1,变轨时在P点点火加速,短时间内将速率由v1增加到v2,使卫星进入椭圆形的转移轨道Ⅱ。
(3)卫星运行到远地点Q时的速率为v3,此时进行第二次点火加速,在短时间内将速率由v3增加到v4,使卫星进入同步轨道Ⅲ,绕地球做匀速圆周运动。
【例3】 (多选)发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后点火,使其沿椭圆轨道2运动,最后再次点火,将卫星送入同步圆轨道3。轨道1、2相切于Q点,轨道2、3相切于P点,如图所示。当卫星分别在1、2、3轨道上正常运动时,以下说法正确的是( )
A.卫星在轨道3上的速率大于在轨道1上的速率
B.卫星在轨道3上的角速度小于在轨道1上的角速度
C.卫星在轨道1上经过Q点时的加速度大小大于它在轨道2上经过Q点时的加速度大小
D.卫星在轨道2上经过P点时的加速度大小等于它在轨道3上经过P点时的加速度大小
思路点拨:(1)不同的圆周运动轨道由v=、ω=比较速率、角速度大小。
(2)由a=比较卫星加速度大小。
BD [由G=m,得v=,因为r3>r1,所以v3<v1,A错误;由G=mrω2,得ω=,因为r3>r1,所以ω3<ω1,B正确;卫星在轨道1上经过Q点时的加速度为地球引力产生的,在轨道2上经过Q点时,也只有地球引力产生加速度,故两者大小应相等,C错误;同理,卫星在轨道2上经过P点时的加速度大小等于它在轨道3上经过P点时的加速度大小,D正确。]
[一语通关]
卫星变轨问题的分析技巧
1.根据引力与需要的向心力的关系分析
(1)当卫星绕天体做匀速圆周运动时,万有引力提供向心力,由G=m,得v=,由此可见轨道半径r越大,线速度v越小。
(2)当由于某原因速度v突然改变时,若速度v减小,则F>m,卫星将做近心运动,轨迹为椭圆;若速度v增大,则F<m,卫星将做离心运动,轨迹为椭圆,此时可用开普勒三定律分析其运动。
2.卫星到达椭圆轨道与圆轨道的切点时,卫星受到的万有引力相同,所以加速度相同。
2.宇宙飞船和空间站在同一轨道上运动,若飞船想与前面的空间站对接,飞船为了追上轨道空间站,可采取的方法是( )
A.飞船加速直到追上空间站,完成对接
B.飞船从原轨道减速至一个较低轨道,再加速追上空间站完成对接
C.飞船加速至一个较高轨道再减速追上空间站完成对接
D.无论飞船采取何种措施,均不能与空间站对接
B [由于宇宙飞船做圆周运动的向心力是地球对其施加的万有引力,由牛顿第二定律有=m,得v=,想追上同轨道上的空间站,直接加速会导致飞船轨道半径增大,由上式知飞船在一个新轨道上运行时速度比空间站的速度小,无法对接,故A错;飞船若先减速,它的轨道半径减小,但速度增大了,故在低轨道上飞船可接近或超过空间站,如图所示。当飞船运动到合适的位置后再加速,则其轨道半径增大,同时速度减小,当刚好运动到空间站所在轨道时停止加速,则飞船的速度刚好等于空间站的速度,可完成对接;若飞船先加速到一个较高轨道,其速度小于空间站速度,此时空间站比飞船运动快,当二者相对运动一周后,使飞船减速,轨道半径减小又使飞船速度增大,仍可追上空间站,但这种方法易造成飞船与空间站碰撞,不是最好的办法,且空间站追飞船不合题意,综上所述,方法应选B。]
[培养层·素养升华]
北斗卫星导航系统
中国北斗卫星导航系统(英文名称:BeiDou Navigation Satellite System,简称BDS)是中国自行研制的全球卫星导航系统,也是继GPS、GLONASS之后的第三个成熟的卫星导航系统。北斗卫星导航系统(BDS)和美国GPS、俄罗斯GLONASS、欧盟GALILEO,是联合国卫星导航委员会已认定的供应商。
北斗卫星导航系统由空间段、地面段和用户段三部分组成,可在全球范围内全天候、全天时为各类用户提供高精度、高可靠定位、导航、授时服务,并具短报文通信能力,已经初步具备区域导航、定位和授时能力,定位精度10米,测速精度0.2米/秒,授时精度10纳秒。
2020年7月31日上午,北斗三号全球卫星导航正式开通。
[设问探究]
1.北斗导航系统中有几颗地球同步卫星,而GPS导航系统由周期为12 h的卫星群组成,两者相比,谁的轨道半径大?谁的线速度大?
2.北斗导航系统中离地球越近的卫星所受的引力越大吗?
提示:1.由周期大的轨道半径大知,北斗导航同步卫星的轨道半径大,又由v=知GPS导航卫星的线速度大。
2.不一定,因卫星的质量不确定。
[深度思考]
1.北斗卫星导航系统(BDS)是我国自行研制的全球卫星导航系统,截止到2019年6月,我国已成功发射了46颗北斗导航卫星,并成功实现组网。其中A、B两颗北斗导航卫星绕地球做匀速圆周运动,SA、SB表示两卫星与地心的连线在单位时间内扫过的面积,vA、vB表示两卫星运行的速率。下列关系式正确的是( )
A.SA=SB B.=
C.= D.无法确定
B [卫星绕地球做匀速圆周运动,则有G=m=mr,由于S=,联立解得S=,由此可知,S与v成反比。选项B正确。]
2.北斗卫星导航系统是我国自行研制开发的区域性三维卫星定位与通信系统(CNSS),建立后的北斗卫星导航系统包括5颗同步卫星和30颗一般轨道卫星。关于这些卫星,以下说法正确的是( )
A.5颗同步卫星的轨道距地高度不同
B.5颗同步卫星的运行轨道不一定在同一平面内
C.导航系统所有卫星的运行速度一定大于第一宇宙速度
D.导航系统所有卫星中,运行轨道半径越大的,周期一定越大
D [因为同步卫星要和地球自转同步,所以运行轨道就在赤道所在平面内,根据F=G=mω2r因为ω一定,所以r必须固定,即一定位于空间同一轨道上且距地高度相同,故A、B错误;第一宇宙速度是近地卫星的环绕速度,也是最大的圆周运动的环绕速度。而同步卫星的轨道半径要大于近地卫星的轨道半径,所以它们运行的线速度一定小于7.9 km/s,故C错误;由公式G=mr得T=, 所以运行轨道半径越大的,周期一定越大,故D正确。故选D。]
[素养点评]
北斗卫星导航系统中有地球的同步卫星,也有非同步卫星,都在自己的轨道上运行,都满足万有引力提供向心力这个规律,能分析它们的周期、角速度、线速度、离地高度等物理量,体现了物理知识在生产生活中的重要性。在分析相关问题时,紧紧抓住F万=F向这个关系式,但是F向的具体表达式要依据分析的问题进行选择,做到具体问题具体分析。
10/10
同课章节目录
- 第一章 抛体运动
- 第一节 曲线运动
- 第二节 运动的合成与分解
- 第三节 平抛运动
- 第四节 生活和生产中的抛体运动
- 第二章 圆周运动
- 第一节 匀速圆周运动
- 第二节 向心力与向心加速度
- 第三节 生活中的圆周运动
- 第四节 离心现象及其应用
- 第三章 万有引力定律
- 第一节 认识天体运动
- 第二节 认识万有引力定律
- 第三节 万有引力定律的应用
- 第四节 宇宙速度与航天
- 第四章 机械能及其守恒定律
- 第一节 功
- 第二节 功率
- 第三节 动能 动能定理
- 第四节 势能
- 第五节 机械能守恒定律
- 第六节 验证机械能守恒定律
- 第七节 生产和生活中的机械能守恒
- 第五章 牛顿力学的局限性与相对论初步
- 第一节 牛顿力学的成就与局限性
- 第二节 相对论时空观
- 第三节 宇宙起源和演化
