粤教版(2019)高中物理 必修第二册 第4章 章末综合提升学案
文档属性
| 名称 | 粤教版(2019)高中物理 必修第二册 第4章 章末综合提升学案 |
|
|
| 格式 | doc | ||
| 文件大小 | 702.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-20 16:31:16 | ||
图片预览



文档简介
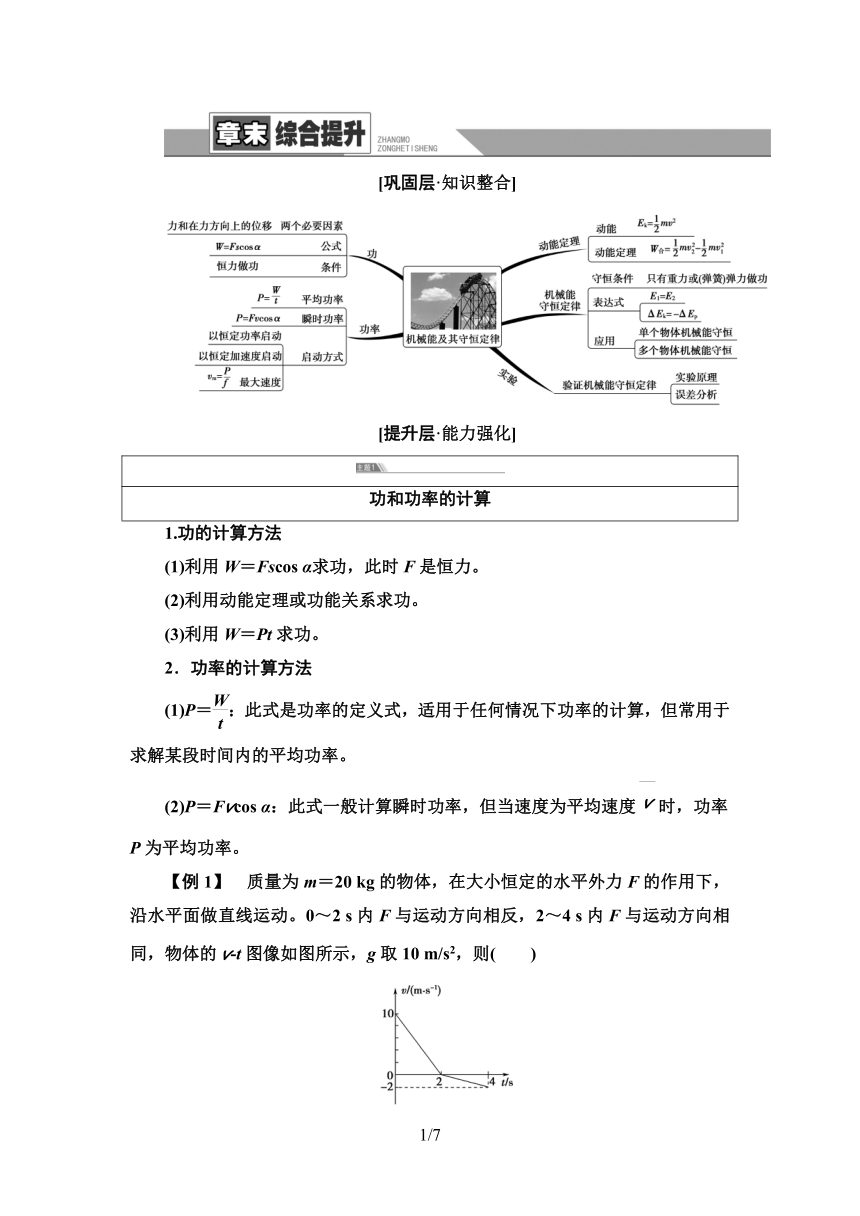
[巩固层·知识整合]
[提升层·能力强化]
功和功率的计算
1.功的计算方法
(1)利用W=Fscos α求功,此时F是恒力。
(2)利用动能定理或功能关系求功。
(3)利用W=Pt求功。
2.功率的计算方法
(1)P=:此式是功率的定义式,适用于任何情况下功率的计算,但常用于求解某段时间内的平均功率。
(2)P=Fvcos α:此式一般计算瞬时功率,但当速度为平均速度时,功率P为平均功率。
【例1】 质量为m=20 kg的物体,在大小恒定的水平外力F的作用下,沿水平面做直线运动。0~2 s内F与运动方向相反,2~4 s内F与运动方向相同,物体的v?t图像如图所示,g取10 m/s2,则( )
A.拉力F的大小为100 N
B.物体在4 s时拉力的瞬时功率为120 W
C.4 s内拉力所做的功为480 J
D.4 s内物体克服摩擦力做的功为320 J
B [由图像可得:0~2 s内物体做匀减速直线运动,加速度大小为:a1== m/s2=5 m/s2,匀减速过程有F+f=ma1。匀加速过程加速度大小为a2== m/s2=1 m/s2,有F-f=ma2,解得f=40 N,F=60 N,故A错误。物体在4 s时拉力的瞬时功率为P=Fv=60×2 W=120 W,故B正确。4 s内物体通过的位移为x=(×2×10-×2×2)m=8 m,拉力做功为W=-Fx=-480 J,故C错误。4 s内物体通过的路程为s=(×2×10+×2×2) m=12 m,摩擦力做功为Wf=-fs=-40×12 J=-480 J,故D错误。]
[一语通关]
抓住v?t图像的两个主要用途
1.v?t图线的斜率表示加速度的大小和方向。
2.v?t图线与坐标轴围成的面积表示位移的大小。
求解动力学的两种思路
1.动力学方法
利用牛顿运动定律结合运动学规律求解力学问题。
2.能量的观点
利用动能定理、机械能守恒定律、能量守恒定律以及功能关系求解力学问题。
【例2】 一质量m=0.6 kg的物体以v0=20 m/s的初速度从倾角α=30°的斜坡底端沿斜坡向上运动。当物体向上滑到某一位置时,其动能减少了ΔEk=18 J,机械能减少了ΔE=3 J。不计空气阻力,重力加速度g取10 m/s2,
求:
(1)物体向上运动时加速度的大小;
(2)物体返回斜坡底端时的动能。
[解析] (1)设物体运动过程中所受的摩擦力为f,向上运动的加速度的大小为a,由牛顿第二定律可知
a= ①
设物体的动能减少ΔEk时,在斜坡上运动的距离为s,由功能关系可知
ΔEk=(mgsin α+f)s ②
ΔE=fs ③
联立①②③式,并代入数据可得
a=6 m/s2。 ④
(2)设物体沿斜坡向上运动的最大距离为sm,由运动学规律可得
sm= ⑤
设物体返回斜坡底端时的动能为Ek,由动能定理得
Ek=(mgsin α-f)sm ⑥
联立①④⑤⑥式,并代入数据可得
Ek=80 J。
[答案] (1)6 m/s2 (2)80 J
[一语通关]
涉及动力学方法和能量观点的综合题,应根据题目要求灵活选用公式和规律。
1.涉及力和运动的瞬时性分析或恒力作用下物体做匀变速直线运动的问题时,可用牛顿运动定律。
2.涉及多过程、变力作用下的问题,不要求知道过程的细节,用功能关系解题简便。
3.只涉及动能与势能的相互转化,单个物体或系统机械能守恒问题时,通常选用机械能守恒定律。
4.涉及多种形式能量转化的问题用能量守恒分析较简便。
解决机械能守恒与圆周运动结合问题的方法
两种分析思路
(1)动力学分析法:在某一个点对物体受力分析,用牛顿第二定律列方程。注意圆周运动的向心力表达式及向心力来源。
(2)功能关系分析法:对物体运动的某一过程应用动能定理或机械能守恒定律列方程,应用动能定理解题只需考虑外力做功和初、末两个状态的动能,并且可以把不同的运动过程合并为一个全过程来处理。机械能守恒定律中守恒条件是只有重力做功或系统内弹簧弹力做功。
【例3】 如图所示,abc是竖直面内的光滑固定轨道,ab水平,长度为2R;bc是半径为R的四分之一圆弧,与ab相切于b点。一质量为m的小球,始终受到与重力大小相等的水平外力的作用,自a点处从静止开始向右运动。重力加速度大小为g。小球从a点开始运动到其轨迹最高点,机械能的增量为( )
A.2mgR B.4mgR
C.5mgR D.6mgR
C [设小球运动到c点的速度大小为vc,则对小球由a到c的过程,由动能定理有F·3R-mgR=mv,又F=mg,解得vc=2,小球离开c点后,在水平方向做初速度为零的匀加速直线运动,竖直方向在重力作用下做匀减速直线运动,由牛顿第二定律可知,小球离开c点后水平方向和竖直方向的加速度大小均为g,则由竖直方向的运动可知,小球从离开c点到其轨迹最高点所需的时间为t==2,在水平方向的位移大小为x=gt2=2R。由以上分析可知,小球从a点开始运动到其轨迹最高点的过程中,水平方向的位移大小为5R,则小球机械能的增加量为ΔE=F·5R=5mgR,C正确,A、B、D错误。]
[一语通关]
该题的两个关键点
1.通过运动过程的分析,找准轨迹的最高点,不要认为c点是轨迹的最高点。
2.机械能的增量等于受到的水平外力做的功。
[培养层·素养升华]
卫星运行与变轨中的机械能问题
2020年3月9日19时55分,我国在西昌卫星发射中心用长征三号乙运载火箭,成功发射北斗系统第五十四颗导航卫星。卫星顺利进入预定轨道,后续将进行变轨、在轨测试、试验评估,适时入网提供服务。
[设问探究]
1.人造卫星绕地球做圆周运动时,它的机械能由哪些形式的能量构成?
2.同一行星的人造卫星变轨前后,其机械能是否改变?举例说明。
提示:1.由动能和重力势能构成,E机=Ek+Ep。
2.改变。若卫星瞬间加速(向后喷气)变轨,动能增大,机械能增大,若卫星瞬间(向前喷气)减速变轨,动能减小,机械能减小。
[深度思考]
1.人造地球卫星在轨道半径较小的轨道A上运行时机械能为EA,它若进入轨道半径较大的轨道B运行时机械能为EB,在轨道变化后这颗卫星( )
A.动能减小,势能增加,EB>EA
B.动能减小,势能增加,EB=EA
C.动能减小,势能增加,EBD.动能增加,势能增加,EB>EA
A [要使卫星由较低轨道进入较高轨道,必须开动发动机使卫星加速,卫星做离心运动。在离心运动过程中万有引力对卫星做负功,卫星运行速度的大小不断减小,动能不断减小而势能增大。由于推力对卫星做了正功,因此卫星机械能变大。]
2.(多选)物体在引力场中具有的势能叫作引力势能。设质量分别为m0和M0的质点相距无穷远时引力势能为零,则相距r0时,其引力势能Ep=-(式中G为引力常量)。一颗质量为m的人造地球卫星在半径为r的圆轨道上环绕地球(地球质量为M)飞行,则卫星轨道半径增大到3 r的过程中( )
A.势能增加了 B.卫星动能减少了
C.机械能增加了 D.机械能减少了
AC [在半径为r的圆轨道上,万有引力提供向心力
G=m
所以动能为Ek1=
势能为Ep1=-
同理,该卫星在3r轨道上运行时动能和势能分别为Ek2=,Ep2=-
计算得势能增加了,A正确;卫星动能减少了,B错误;机械能增加了,C正确,D错误;故选AC。]
[素养点评]
北斗导航系统是中国自行研制的全球卫星导航系统,它是中国的骄傲。卫星在变轨时,机械能发生变化,卫星在轨道上正常运行时,机械能守恒。同时卫星的受力与运动也满足万有引力定律和牛顿第二定律,它是物理知识在科研中的综合应用,体现了科学的思维方法和科学的态度与责任。
6/6
[提升层·能力强化]
功和功率的计算
1.功的计算方法
(1)利用W=Fscos α求功,此时F是恒力。
(2)利用动能定理或功能关系求功。
(3)利用W=Pt求功。
2.功率的计算方法
(1)P=:此式是功率的定义式,适用于任何情况下功率的计算,但常用于求解某段时间内的平均功率。
(2)P=Fvcos α:此式一般计算瞬时功率,但当速度为平均速度时,功率P为平均功率。
【例1】 质量为m=20 kg的物体,在大小恒定的水平外力F的作用下,沿水平面做直线运动。0~2 s内F与运动方向相反,2~4 s内F与运动方向相同,物体的v?t图像如图所示,g取10 m/s2,则( )
A.拉力F的大小为100 N
B.物体在4 s时拉力的瞬时功率为120 W
C.4 s内拉力所做的功为480 J
D.4 s内物体克服摩擦力做的功为320 J
B [由图像可得:0~2 s内物体做匀减速直线运动,加速度大小为:a1== m/s2=5 m/s2,匀减速过程有F+f=ma1。匀加速过程加速度大小为a2== m/s2=1 m/s2,有F-f=ma2,解得f=40 N,F=60 N,故A错误。物体在4 s时拉力的瞬时功率为P=Fv=60×2 W=120 W,故B正确。4 s内物体通过的位移为x=(×2×10-×2×2)m=8 m,拉力做功为W=-Fx=-480 J,故C错误。4 s内物体通过的路程为s=(×2×10+×2×2) m=12 m,摩擦力做功为Wf=-fs=-40×12 J=-480 J,故D错误。]
[一语通关]
抓住v?t图像的两个主要用途
1.v?t图线的斜率表示加速度的大小和方向。
2.v?t图线与坐标轴围成的面积表示位移的大小。
求解动力学的两种思路
1.动力学方法
利用牛顿运动定律结合运动学规律求解力学问题。
2.能量的观点
利用动能定理、机械能守恒定律、能量守恒定律以及功能关系求解力学问题。
【例2】 一质量m=0.6 kg的物体以v0=20 m/s的初速度从倾角α=30°的斜坡底端沿斜坡向上运动。当物体向上滑到某一位置时,其动能减少了ΔEk=18 J,机械能减少了ΔE=3 J。不计空气阻力,重力加速度g取10 m/s2,
求:
(1)物体向上运动时加速度的大小;
(2)物体返回斜坡底端时的动能。
[解析] (1)设物体运动过程中所受的摩擦力为f,向上运动的加速度的大小为a,由牛顿第二定律可知
a= ①
设物体的动能减少ΔEk时,在斜坡上运动的距离为s,由功能关系可知
ΔEk=(mgsin α+f)s ②
ΔE=fs ③
联立①②③式,并代入数据可得
a=6 m/s2。 ④
(2)设物体沿斜坡向上运动的最大距离为sm,由运动学规律可得
sm= ⑤
设物体返回斜坡底端时的动能为Ek,由动能定理得
Ek=(mgsin α-f)sm ⑥
联立①④⑤⑥式,并代入数据可得
Ek=80 J。
[答案] (1)6 m/s2 (2)80 J
[一语通关]
涉及动力学方法和能量观点的综合题,应根据题目要求灵活选用公式和规律。
1.涉及力和运动的瞬时性分析或恒力作用下物体做匀变速直线运动的问题时,可用牛顿运动定律。
2.涉及多过程、变力作用下的问题,不要求知道过程的细节,用功能关系解题简便。
3.只涉及动能与势能的相互转化,单个物体或系统机械能守恒问题时,通常选用机械能守恒定律。
4.涉及多种形式能量转化的问题用能量守恒分析较简便。
解决机械能守恒与圆周运动结合问题的方法
两种分析思路
(1)动力学分析法:在某一个点对物体受力分析,用牛顿第二定律列方程。注意圆周运动的向心力表达式及向心力来源。
(2)功能关系分析法:对物体运动的某一过程应用动能定理或机械能守恒定律列方程,应用动能定理解题只需考虑外力做功和初、末两个状态的动能,并且可以把不同的运动过程合并为一个全过程来处理。机械能守恒定律中守恒条件是只有重力做功或系统内弹簧弹力做功。
【例3】 如图所示,abc是竖直面内的光滑固定轨道,ab水平,长度为2R;bc是半径为R的四分之一圆弧,与ab相切于b点。一质量为m的小球,始终受到与重力大小相等的水平外力的作用,自a点处从静止开始向右运动。重力加速度大小为g。小球从a点开始运动到其轨迹最高点,机械能的增量为( )
A.2mgR B.4mgR
C.5mgR D.6mgR
C [设小球运动到c点的速度大小为vc,则对小球由a到c的过程,由动能定理有F·3R-mgR=mv,又F=mg,解得vc=2,小球离开c点后,在水平方向做初速度为零的匀加速直线运动,竖直方向在重力作用下做匀减速直线运动,由牛顿第二定律可知,小球离开c点后水平方向和竖直方向的加速度大小均为g,则由竖直方向的运动可知,小球从离开c点到其轨迹最高点所需的时间为t==2,在水平方向的位移大小为x=gt2=2R。由以上分析可知,小球从a点开始运动到其轨迹最高点的过程中,水平方向的位移大小为5R,则小球机械能的增加量为ΔE=F·5R=5mgR,C正确,A、B、D错误。]
[一语通关]
该题的两个关键点
1.通过运动过程的分析,找准轨迹的最高点,不要认为c点是轨迹的最高点。
2.机械能的增量等于受到的水平外力做的功。
[培养层·素养升华]
卫星运行与变轨中的机械能问题
2020年3月9日19时55分,我国在西昌卫星发射中心用长征三号乙运载火箭,成功发射北斗系统第五十四颗导航卫星。卫星顺利进入预定轨道,后续将进行变轨、在轨测试、试验评估,适时入网提供服务。
[设问探究]
1.人造卫星绕地球做圆周运动时,它的机械能由哪些形式的能量构成?
2.同一行星的人造卫星变轨前后,其机械能是否改变?举例说明。
提示:1.由动能和重力势能构成,E机=Ek+Ep。
2.改变。若卫星瞬间加速(向后喷气)变轨,动能增大,机械能增大,若卫星瞬间(向前喷气)减速变轨,动能减小,机械能减小。
[深度思考]
1.人造地球卫星在轨道半径较小的轨道A上运行时机械能为EA,它若进入轨道半径较大的轨道B运行时机械能为EB,在轨道变化后这颗卫星( )
A.动能减小,势能增加,EB>EA
B.动能减小,势能增加,EB=EA
C.动能减小,势能增加,EB
A [要使卫星由较低轨道进入较高轨道,必须开动发动机使卫星加速,卫星做离心运动。在离心运动过程中万有引力对卫星做负功,卫星运行速度的大小不断减小,动能不断减小而势能增大。由于推力对卫星做了正功,因此卫星机械能变大。]
2.(多选)物体在引力场中具有的势能叫作引力势能。设质量分别为m0和M0的质点相距无穷远时引力势能为零,则相距r0时,其引力势能Ep=-(式中G为引力常量)。一颗质量为m的人造地球卫星在半径为r的圆轨道上环绕地球(地球质量为M)飞行,则卫星轨道半径增大到3 r的过程中( )
A.势能增加了 B.卫星动能减少了
C.机械能增加了 D.机械能减少了
AC [在半径为r的圆轨道上,万有引力提供向心力
G=m
所以动能为Ek1=
势能为Ep1=-
同理,该卫星在3r轨道上运行时动能和势能分别为Ek2=,Ep2=-
计算得势能增加了,A正确;卫星动能减少了,B错误;机械能增加了,C正确,D错误;故选AC。]
[素养点评]
北斗导航系统是中国自行研制的全球卫星导航系统,它是中国的骄傲。卫星在变轨时,机械能发生变化,卫星在轨道上正常运行时,机械能守恒。同时卫星的受力与运动也满足万有引力定律和牛顿第二定律,它是物理知识在科研中的综合应用,体现了科学的思维方法和科学的态度与责任。
6/6
同课章节目录
- 第一章 抛体运动
- 第一节 曲线运动
- 第二节 运动的合成与分解
- 第三节 平抛运动
- 第四节 生活和生产中的抛体运动
- 第二章 圆周运动
- 第一节 匀速圆周运动
- 第二节 向心力与向心加速度
- 第三节 生活中的圆周运动
- 第四节 离心现象及其应用
- 第三章 万有引力定律
- 第一节 认识天体运动
- 第二节 认识万有引力定律
- 第三节 万有引力定律的应用
- 第四节 宇宙速度与航天
- 第四章 机械能及其守恒定律
- 第一节 功
- 第二节 功率
- 第三节 动能 动能定理
- 第四节 势能
- 第五节 机械能守恒定律
- 第六节 验证机械能守恒定律
- 第七节 生产和生活中的机械能守恒
- 第五章 牛顿力学的局限性与相对论初步
- 第一节 牛顿力学的成就与局限性
- 第二节 相对论时空观
- 第三节 宇宙起源和演化
