人教版八年级数学上册一课一练11.3 多边形及其内角和(word版,含答案)
文档属性
| 名称 | 人教版八年级数学上册一课一练11.3 多边形及其内角和(word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 644.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-20 00:00:00 | ||
图片预览


文档简介
11.3
多边形及其内角和
一、选择题(共10小题;共50分)
1.
下列图形中,能镶嵌成平面图案的是
A.
正六边形
B.
正七边形
C.
正八边形
D.
正九边形
2.
一个多边形的每个内角均为
,则这个多边形是
A.
七边形
B.
六边形
C.
五边形
D.
四边形
3.
从六边形的一个顶点出发,可以画出
条对角线,它们将六边形分成
个三角形.则
,
的值分别为
A.
B.
C.
D.
4.
某市“佳美大剧院”即将完工,现需选用同一批地砖进行装修,以下不能密铺的地砖是
A.
正五边形地砖
B.
正三角形地砖
C.
正六边形地砖
D.
正四边形地砖
5.
若从多边形的一个顶点可以引出
条对角线,则这个多边形是
A.
七边形
B.
八边形
C.
九边形
D.
十边形
6.
已知实数
,
满足
,则以
,
的值为两边长的等腰三角形的周长是
A.
或
B.
C.
D.
以上答案均不对
7.
下列边长相等的正多边形能够密铺的组合是
A.
正八边形和正方形
B.
正五边形和正九边形
C.
正方形和正六边形
D.
正方形和正七边形
8.
在下列四种边长均为
的正多边形中,能与边长为
的正三角形进行平面密铺的正多边形有
①正方形;②正五边形;③正六边形;④正八边形.
A.
种
B.
种
C.
种
D.
种
9.
如图,五边形
中,,,,
分别是
,,
的外角,则
等于
A.
B.
C.
D.
10.
一个多边形的内角和是外角和的
倍,则这个多边形是
A.
四边形
B.
五边形
C.
六边形
D.
八边形
二、填空题(共6小题;共48分)
11.
一个多边形的内角和为
,则这个多边形是
?边形.
12.
过
边形的一个顶点可作
?
条对角线,可将
边形分成
?
个三角形.
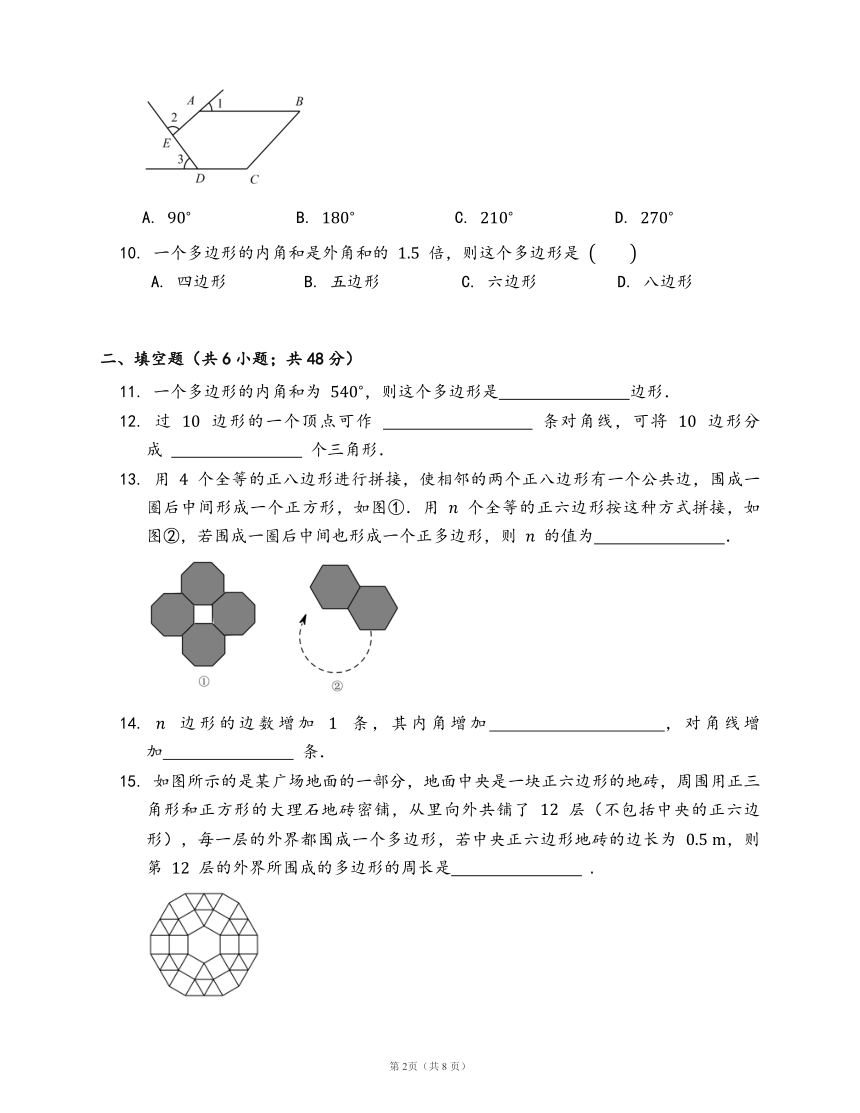
13.
用
个全等的正八边形进行拼接,使相邻的两个正八边形有一个公共边,围成一圈后中间形成一个正方形,如图①.用
个全等的正六边形按这种方式拼接,如图②,若围成一圈后中间也形成一个正多边形,则
的值为
?.
14.
边形的边数增加
条,其内角增加
?,对角线增加
?
条.
15.
如图所示的是某广场地面的一部分,地面中央是一块正六边形的地砖,周围用正三角形和正方形的大理石地砖密铺,从里向外共铺了
层(不包括中央的正六边形),每一层的外界都围成一个多边形,若中央正六边形地砖的边长为
,则第
层的外界所围成的多边形的周长是
?
16.
如图,正六边形
内部有一个正五边形
,且
,直线
经过
,,则直线
与
的夹角
?
.
三、解答题(共4小题;共52分)
17.
试说明正八边形不能铺满平面的理由.
18.
正三角形、正方形、正六边形(如图1)是我们熟悉的特殊多边形.
(1)这些图形中的边与角有什么共同特征?
一般地,我们把各边相等、各内角也相等的多边形叫做正多边形(regular
polygon).边数为五的正多边形叫做正五边形(如图2),
边数为六的正多边形叫做正六边形,如图3的两个正多边形分别是正七边形和正八边形.
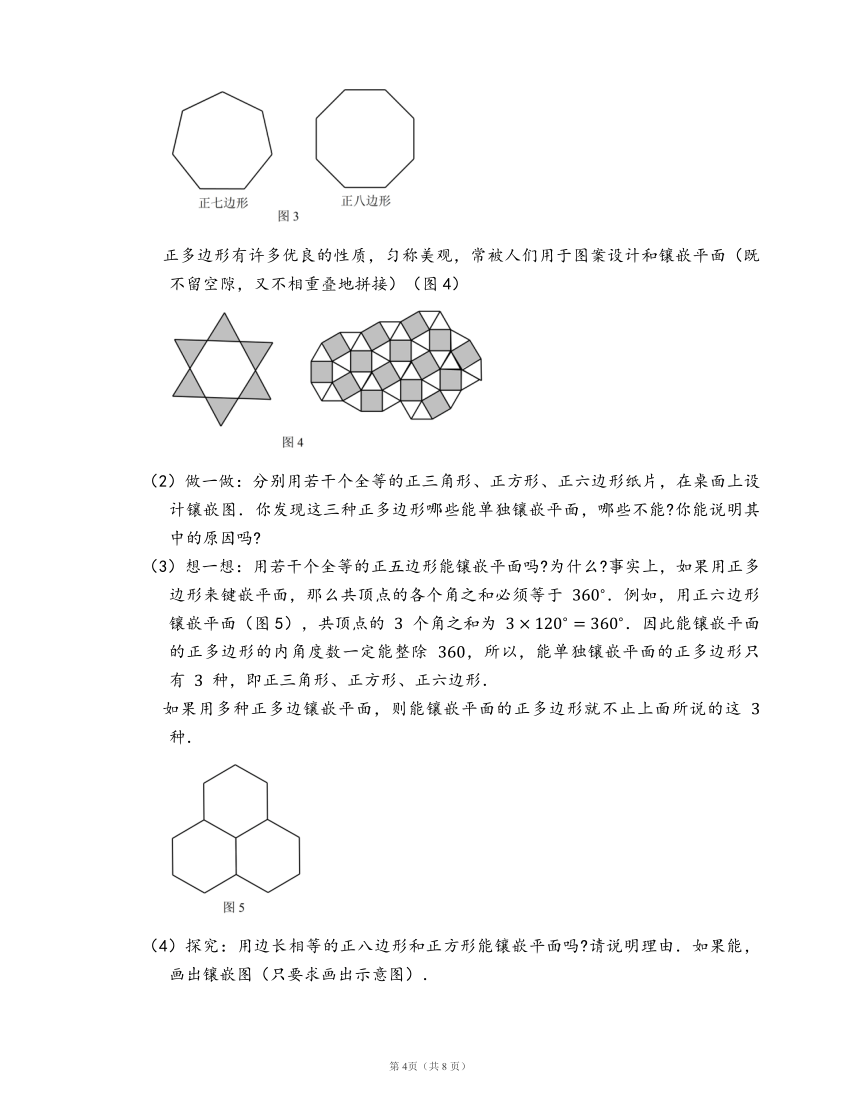
正多边形有许多优良的性质,匀称美观,常被人们用于图案设计和镶嵌平面(既不留空隙,又不相重叠地拼接)(图4)
(2)做一做:分别用若干个全等的正三角形、正方形、正六边形纸片,在桌面上设计镶嵌图.你发现这三种正多边形哪些能单独镶嵌平面,哪些不能?你能说明其中的原因吗?
(3)想一想:用若干个全等的正五边形能镶嵌平面吗?为什么?事实上,如果用正多边形来键嵌平面,那么共顶点的各个角之和必须等于
.例如,用正六边形镶嵌平面(图5),共顶点的
个角之和为
.因此能镶嵌平面的正多边形的内角度数一定能整除
,所以,能单独镶嵌平面的正多边形只有
种,即正三角形、正方形、正六边形.
如果用多种正多边镶嵌平面,则能镶嵌平面的正多边形就不止上面所说的这
种.
(4)探究:用边长相等的正八边形和正方形能镶嵌平面吗?请说明理由.如果能,画出镶嵌图(只要求画出示意图).
19.
如图,凸六边形
的六个角都是
,边长
,,,,你能求出这个六边形的周长吗?
20.
奥地利数学家皮克发现了一个计算正方形网格纸中多边形面积的公式:,方格纸中每个小正方形的边长为
,其中
表示多边形内部的格点数,
表示多边形边界上的格点数,
表示多边形的面积.
注:①由
条线段依次首尾连接而成的封闭图形叫做
边形,这些线段的端点叫做顶点.
②网格中小正方形的顶点叫格点.
如:在图①中,点
,,,
都正好在格点上,那么四边形
的面积
.
(1)求图②中四边形
的面积.
(2)若多边形的顶点都在格点上,且面积为
,请在图③④⑤中画出这样三个形状不同的多边形(多边形的边数
).并写出相应的
,
的值.
图③中,
?
,
?;图④中,
?,
?;图⑤中,
?,
?.
答案
第一部分
1.
A
2.
C
3.
C
4.
A
【解析】五边形每个内角是
,不是
的约数,不能密铺,符合题意;正三角形的一个内角度数为
,是
的约数,能密铺,不符合题意;正六边形的一个内角度数为
,是
的约数,能密铺,不符合题意;正四边形的一个内角度数为
,是
的约数,能密铺,不符合题意
5.
D
【解析】因为从多边形的一个顶点可引出
条对角线,
所以
,
所以
.
6.
B
7.
A
8.
C
【解析】①③可以
9.
B
【解析】如答图,延长
,,
,
,,
.
根据多边形的外角和定理,得
,
.
10.
B
【解析】设这个多边形
边形,
根据题意,得
,
解得:.
即这个多边形为五边形.
第二部分
11.
五
12.
,
13.
14.
,
【解析】
边形的对角线有
条,
边形的对角线有
条,
.
15.
【解析】第
层是
边形,
第
层是
边形,
每层都比前一层多
条边
第
层是
边形,
.
16.
第三部分
17.
正八边形一个内角的度数是
,
不能被
整除,两个内角的和小于
,三个内角的和大于
,
所以正八边形不能铺满平面.
18.
(1)
正三角形、正方形、正六边形的共同特征是各个内角都相等,各条边都相等.
??????(2)
做一做:正三角形、正方形、正六边形都能单独镶嵌平面,因为正三角形的一个内角为
,将
个正三角形拼在一起,共顶点的
个角之和为
,刚好拼成一个周角.
??????(3)
想一想:正五边形不能单独镶嵌平面,因为正五边形的一个内角为
.
个内角和为
,
个内角和为
,不能拼成周角.
??????(4)
探究:用边长相等的正八边形和正方形能镶嵌平面因为正八边形的内角
,正方形的内角为
,由于
,所以两个正八边形和一个正方形能拼成一幅镶嵌图(如图).
19.
如图,分别作直线
、
、
的延长线使它们交于点
、
、
.
因为六边形
的六个角都是
,
所以六边形
的每一个外角的度数都是
.
所以三角形
、三角形
、三角形
、三角形
都是等边三角形.
所以
,.
所以
,,.
所以六边形的周长为
.
20.
(1)
由题意,得
,,
.
??????(2)
由题意得,图象可以如图所示.
则图③中,,;
图④中,,;
图⑤中,,.
第5页(共8
页)
多边形及其内角和
一、选择题(共10小题;共50分)
1.
下列图形中,能镶嵌成平面图案的是
A.
正六边形
B.
正七边形
C.
正八边形
D.
正九边形
2.
一个多边形的每个内角均为
,则这个多边形是
A.
七边形
B.
六边形
C.
五边形
D.
四边形
3.
从六边形的一个顶点出发,可以画出
条对角线,它们将六边形分成
个三角形.则
,
的值分别为
A.
B.
C.
D.
4.
某市“佳美大剧院”即将完工,现需选用同一批地砖进行装修,以下不能密铺的地砖是
A.
正五边形地砖
B.
正三角形地砖
C.
正六边形地砖
D.
正四边形地砖
5.
若从多边形的一个顶点可以引出
条对角线,则这个多边形是
A.
七边形
B.
八边形
C.
九边形
D.
十边形
6.
已知实数
,
满足
,则以
,
的值为两边长的等腰三角形的周长是
A.
或
B.
C.
D.
以上答案均不对
7.
下列边长相等的正多边形能够密铺的组合是
A.
正八边形和正方形
B.
正五边形和正九边形
C.
正方形和正六边形
D.
正方形和正七边形
8.
在下列四种边长均为
的正多边形中,能与边长为
的正三角形进行平面密铺的正多边形有
①正方形;②正五边形;③正六边形;④正八边形.
A.
种
B.
种
C.
种
D.
种
9.
如图,五边形
中,,,,
分别是
,,
的外角,则
等于
A.
B.
C.
D.
10.
一个多边形的内角和是外角和的
倍,则这个多边形是
A.
四边形
B.
五边形
C.
六边形
D.
八边形
二、填空题(共6小题;共48分)
11.
一个多边形的内角和为
,则这个多边形是
?边形.
12.
过
边形的一个顶点可作
?
条对角线,可将
边形分成
?
个三角形.
13.
用
个全等的正八边形进行拼接,使相邻的两个正八边形有一个公共边,围成一圈后中间形成一个正方形,如图①.用
个全等的正六边形按这种方式拼接,如图②,若围成一圈后中间也形成一个正多边形,则
的值为
?.
14.
边形的边数增加
条,其内角增加
?,对角线增加
?
条.
15.
如图所示的是某广场地面的一部分,地面中央是一块正六边形的地砖,周围用正三角形和正方形的大理石地砖密铺,从里向外共铺了
层(不包括中央的正六边形),每一层的外界都围成一个多边形,若中央正六边形地砖的边长为
,则第
层的外界所围成的多边形的周长是
?
16.
如图,正六边形
内部有一个正五边形
,且
,直线
经过
,,则直线
与
的夹角
?
.
三、解答题(共4小题;共52分)
17.
试说明正八边形不能铺满平面的理由.
18.
正三角形、正方形、正六边形(如图1)是我们熟悉的特殊多边形.
(1)这些图形中的边与角有什么共同特征?
一般地,我们把各边相等、各内角也相等的多边形叫做正多边形(regular
polygon).边数为五的正多边形叫做正五边形(如图2),
边数为六的正多边形叫做正六边形,如图3的两个正多边形分别是正七边形和正八边形.
正多边形有许多优良的性质,匀称美观,常被人们用于图案设计和镶嵌平面(既不留空隙,又不相重叠地拼接)(图4)
(2)做一做:分别用若干个全等的正三角形、正方形、正六边形纸片,在桌面上设计镶嵌图.你发现这三种正多边形哪些能单独镶嵌平面,哪些不能?你能说明其中的原因吗?
(3)想一想:用若干个全等的正五边形能镶嵌平面吗?为什么?事实上,如果用正多边形来键嵌平面,那么共顶点的各个角之和必须等于
.例如,用正六边形镶嵌平面(图5),共顶点的
个角之和为
.因此能镶嵌平面的正多边形的内角度数一定能整除
,所以,能单独镶嵌平面的正多边形只有
种,即正三角形、正方形、正六边形.
如果用多种正多边镶嵌平面,则能镶嵌平面的正多边形就不止上面所说的这
种.
(4)探究:用边长相等的正八边形和正方形能镶嵌平面吗?请说明理由.如果能,画出镶嵌图(只要求画出示意图).
19.
如图,凸六边形
的六个角都是
,边长
,,,,你能求出这个六边形的周长吗?
20.
奥地利数学家皮克发现了一个计算正方形网格纸中多边形面积的公式:,方格纸中每个小正方形的边长为
,其中
表示多边形内部的格点数,
表示多边形边界上的格点数,
表示多边形的面积.
注:①由
条线段依次首尾连接而成的封闭图形叫做
边形,这些线段的端点叫做顶点.
②网格中小正方形的顶点叫格点.
如:在图①中,点
,,,
都正好在格点上,那么四边形
的面积
.
(1)求图②中四边形
的面积.
(2)若多边形的顶点都在格点上,且面积为
,请在图③④⑤中画出这样三个形状不同的多边形(多边形的边数
).并写出相应的
,
的值.
图③中,
?
,
?;图④中,
?,
?;图⑤中,
?,
?.
答案
第一部分
1.
A
2.
C
3.
C
4.
A
【解析】五边形每个内角是
,不是
的约数,不能密铺,符合题意;正三角形的一个内角度数为
,是
的约数,能密铺,不符合题意;正六边形的一个内角度数为
,是
的约数,能密铺,不符合题意;正四边形的一个内角度数为
,是
的约数,能密铺,不符合题意
5.
D
【解析】因为从多边形的一个顶点可引出
条对角线,
所以
,
所以
.
6.
B
7.
A
8.
C
【解析】①③可以
9.
B
【解析】如答图,延长
,,
,
,,
.
根据多边形的外角和定理,得
,
.
10.
B
【解析】设这个多边形
边形,
根据题意,得
,
解得:.
即这个多边形为五边形.
第二部分
11.
五
12.
,
13.
14.
,
【解析】
边形的对角线有
条,
边形的对角线有
条,
.
15.
【解析】第
层是
边形,
第
层是
边形,
每层都比前一层多
条边
第
层是
边形,
.
16.
第三部分
17.
正八边形一个内角的度数是
,
不能被
整除,两个内角的和小于
,三个内角的和大于
,
所以正八边形不能铺满平面.
18.
(1)
正三角形、正方形、正六边形的共同特征是各个内角都相等,各条边都相等.
??????(2)
做一做:正三角形、正方形、正六边形都能单独镶嵌平面,因为正三角形的一个内角为
,将
个正三角形拼在一起,共顶点的
个角之和为
,刚好拼成一个周角.
??????(3)
想一想:正五边形不能单独镶嵌平面,因为正五边形的一个内角为
.
个内角和为
,
个内角和为
,不能拼成周角.
??????(4)
探究:用边长相等的正八边形和正方形能镶嵌平面因为正八边形的内角
,正方形的内角为
,由于
,所以两个正八边形和一个正方形能拼成一幅镶嵌图(如图).
19.
如图,分别作直线
、
、
的延长线使它们交于点
、
、
.
因为六边形
的六个角都是
,
所以六边形
的每一个外角的度数都是
.
所以三角形
、三角形
、三角形
、三角形
都是等边三角形.
所以
,.
所以
,,.
所以六边形的周长为
.
20.
(1)
由题意,得
,,
.
??????(2)
由题意得,图象可以如图所示.
则图③中,,;
图④中,,;
图⑤中,,.
第5页(共8
页)
