3.3 万有引力定律的应用课件29张PPT
文档属性
| 名称 | 3.3 万有引力定律的应用课件29张PPT |
|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-20 00:00:00 | ||
图片预览







文档简介
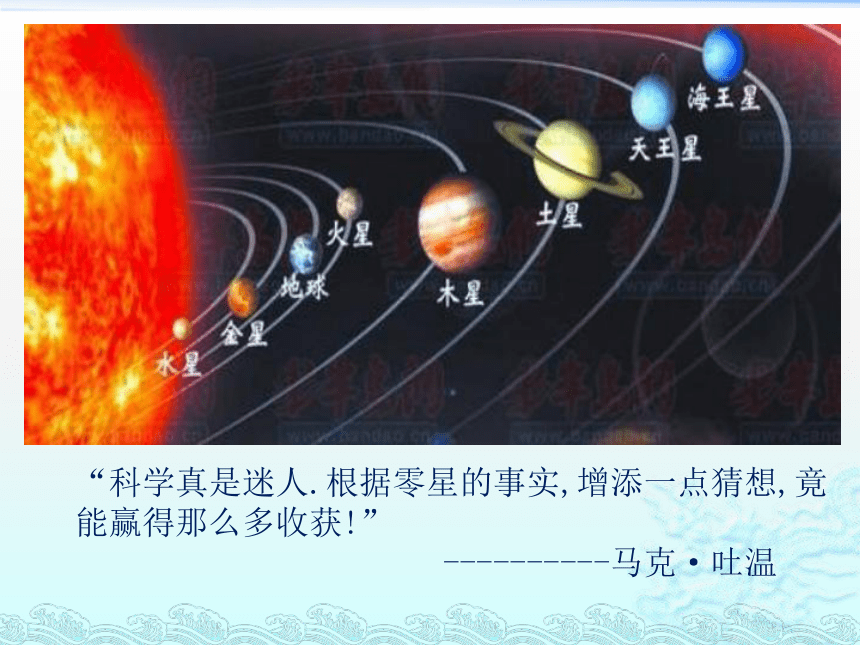
哈雷彗星
一个成功的理论不仅要解释已知的事实,更重要的是能预言未知的现象。
“科学真是迷人.根据零星的事实,增添一点猜想,竟能赢得那么多收获!”
----------马克·吐温
3.3万有引力定律的应用
四川省广安代市中学校
黄青平
1705年哈雷根据牛顿的引力理论,计算了 “哈雷彗星”的轨道并正确预言了它的回归
预言彗星回归
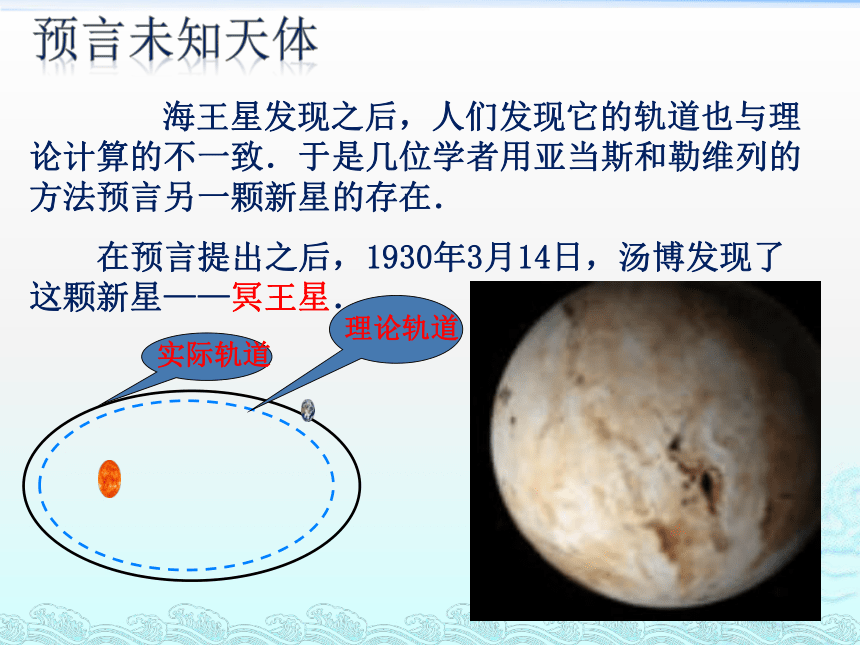
预言未知天体
亚当斯与勒维烈预测在天王星附近还有一颗行星
1781年英国天文学家威廉.赫歇耳用望远镜发现了天王星
1821年,天王星的实际轨道与理论轨道存在较大的误差
猜想:……….
1846年9月23日,海王星被发现。
海王星
“笔尖下发现的行星”
理论轨道
实际轨道
海王星发现之后,人们发现它的轨道也与理论计算的不一致.于是几位学者用亚当斯和勒维列的方法预言另一颗新星的存在.
在预言提出之后,1930年3月14日,汤博发现了这颗新星——冥王星.
预言未知天体
美国2001年发射,并于2006至2008年访问冥王星的宇宙飞船
诺贝尔物理学奖获得者
物理学家冯·劳厄说:
“没有任何东西像牛顿引力理论对行星轨道的计算那样,如此有力地树立起人们对年轻的物理学的尊敬。从此以后,这门自然科学成了巨大的精神王国…… ”
阿基米德在研究杠杆原理后,曾经说过一句什么名言?
“给我一个支点,我可以撬动球。”
那我们又是怎么知道巨大的地球的质量呢?
那给我们一个杠杆(天平)是否就可以称量地球的质量了呢?
答案:不能
测量巨大的天体质量显然只能采用间接的方法.
卡文迪许在实验室称量出了地球的质量!
问题一: 如何测量地球的质量?
思考:卡文迪许是如何“称量”地球的质量的呢?
能否通过万有引力定律来“称量”呢?
时代背景:
当时已知地球的半径R,地球表面重力加速度g及卡文迪许已测出的引力常量G
1.若不考虑地球自转的影响,地面上的物体的重力等于地球对它的引力。
由于g、R在卡文迪许之前已经知道,而卡文迪许测出G后,就意味着也测出了地球的质量。
卡文迪许被称为“第一个称量地球质量的人”!
2.关系式:
3.地球的质量到底有多大?
已知:地球表面g=9.8m/s2,地球半径R=6370km,引力常量G=6.67×10-11N.m2/kg2
请你根据这些数据计算地球的质量M。
代入数据有:
思考:
1.哪些运动的加速度是g?
思考:
2.哪些力的大小与g值有关联?
问题二: 如何测量太阳的质量?
思考:太阳是一个火热的球体,我们无法得知其上的重力加速度,那如何来求太阳的质量呢?
从以下几个方面去考虑:
圆轨道做匀速圆周运动
椭圆
为了解决问题的方便,我们通常可以认为地球在绕怎样的轨道做什么运动?
近似
(1)地球公转实际轨道是什么形状?
(2)地球作圆周运动的向心力是由谁来提供的?
太阳对地球的引力,即F引=F向
(3)动力学方程——万有引力充当向心力
求出太阳的质量
F引=F向 即
明确式中各符号所代表的物理量:
r 代表:
T 代表:
公转轨道半径
公转周期
(4)思考
不需要
相同
②不同的行星r和T各不相同,但计算出来的太阳质量是否一定相同呢?
①测量太阳的质量,是否需要知道行星的质量?
同样的道理,如果已知卫星绕行星运动的周期和卫星与行星之间的距离,也可以算出行星的质量。目前,观测人造卫星的运动,是测量地球质量的重要方法之一。
例1.为了研究太阳演化进程,需知道太阳的质量M.已知地球的半径 R=6.4×106 m,地球的质量 m=6×1024 kg,日地中心的距离 r=1.5×1011 m,地球表面的重力加速度 g=10m/s2,1年约为 3.2×107 s,试估算太阳的质量M.(引力常数未知)
解:由万有引力定律和动力学知识得
对地球表面的物体m′,有
联立两式得
代入数据得
方法一 :测“g”法( 重力近似等于万有引力)
基本思路:
“黄金”代换公式!
根据前面的探究,请同学们归纳总结计算天体的质量的基本思路。
方法二:环绕法 (万有引力充当向心力)
基本思路:
中心天体
环绕天体
M
r
m
能计算月球的质量吗?
只能计算中心天体的质量
不能计算环绕天体的质量
例2、一艘宇宙飞船飞近某一新发现的行星,并进入靠近该行星表面的圆形轨道运行数圈后,着陆在该行星上,宇宙飞船上备有以下实验器材:A.精确秒表一只 B.质量为m的物体一个 C.弹簧秤一只 D.天平一架(包括砝码一套)。已知宇航员在绕行及着陆后各做一次测量,根据所测量的数据可以求出该星球的质量M、半径R(已知万有引力恒量为G)。
(1)两次测量的物理量分别为___________________
(2)两次测量所选用的仪器分别为_______.(用该仪器的字母序号表示).
(3)用所测值可求出星球的质量M=__________
半径R=___________
绕行周期T和物体的重力F
A、C
例3.已知地球与火星的质量之比M地∶M火=8∶1。半径之比R地∶R火=2∶1,在地球表面固定一水平木板,板上再放一个箱子,已知箱子与木板之间的动摩擦因数为0.5,现用水平拉力拖动箱子时,能获得10 m/s2的最大加速度,将箱子、木板送到火星上,仍用同样的力和方式拖动箱子,求此箱子能获得的最大加速度。(g=10 m/s2)
解:在星球表面:
在地球表面拖动,由F合=ma得:
F-μmg地=ma地
在火星表面拖动,同理得:
解上述各式有:a火=μ(g地-g火)+g地=12.5 m/s2
F-μmg火=ma火
问题三: 如何计算天体的密度?
问题三: 如何计算天体的密度?
若T是近地卫星的周期,则r≈R
例4.利用下列哪组数据可以算出地球的质量( )
A、已知地球的半径 R 和地球表面的重力加速度 g
B、已知地球半径R和月球公转周期
C、已知卫星围绕地球运动的轨道半径 r 和角速度ω
D、已知卫星围绕地球运动的线速度 v和周期T
E、已知日地距离及地球绕太阳的公转周期
F、已知地球自转周期和地球半径
G、已知绕地球表面运动的卫星周期T
H、已知绕地球表面运动的卫星周期T和地表g
I、一种地球自转周期T和同步卫星的半径r
ACDHI
例5.利用下列哪些数据可以算出地球的密度( )
A、已知地球的半径 R 和地球表面的重力加速度 g
B、已知地球半径R和月球公转周期
C、已知卫星围绕地球运动的轨道半径 r 和角速度ω
D、已知卫星围绕地球运动的线速度 v和周期T
E、已知日地距离及地球绕太阳的公转周期
F、已知地球自转周期和地球半径
G、已知绕地球表面运动的卫星周期T
H、已知绕地球表面运动的卫星周期T和地表g
I、一种地球自转周期T和同步卫星的半径r
AGH
V0
P
A
2V0
Q
O
H
例6.宇航员站在星球表面上某高处,沿水平方向抛出一小球,经过时间t小球落回星球表面,测得抛出点和落地点之间的距离为L。若抛出时的速度增大为原来的2倍,则抛出点到落地点之间的距离为 。已知两落地点在同一水平面上,求:(1)此星球表面的重力加速度(2)忽略星球自转,若该星球半径为R,求该星球的质量M。
V0
P
A
2V0
Q
O
H
答案:
求:(1)此星球表面的重力加速度(2)忽略星球自转,若该星球半径为R,求该星球的质量M。
例7.《教材》P51 发展空间:估测太阳的密度
所测的物理量:
测量原理:
测量说明:
1、观测时间:
先测质量、再测D和d
地球的公转周期T和测D和d
早晨或傍晚或有保护眼睛的工具
2、测D和d:
小孔成像法
一个成功的理论不仅要解释已知的事实,更重要的是能预言未知的现象。
“科学真是迷人.根据零星的事实,增添一点猜想,竟能赢得那么多收获!”
----------马克·吐温
3.3万有引力定律的应用
四川省广安代市中学校
黄青平
1705年哈雷根据牛顿的引力理论,计算了 “哈雷彗星”的轨道并正确预言了它的回归
预言彗星回归
预言未知天体
亚当斯与勒维烈预测在天王星附近还有一颗行星
1781年英国天文学家威廉.赫歇耳用望远镜发现了天王星
1821年,天王星的实际轨道与理论轨道存在较大的误差
猜想:……….
1846年9月23日,海王星被发现。
海王星
“笔尖下发现的行星”
理论轨道
实际轨道
海王星发现之后,人们发现它的轨道也与理论计算的不一致.于是几位学者用亚当斯和勒维列的方法预言另一颗新星的存在.
在预言提出之后,1930年3月14日,汤博发现了这颗新星——冥王星.
预言未知天体
美国2001年发射,并于2006至2008年访问冥王星的宇宙飞船
诺贝尔物理学奖获得者
物理学家冯·劳厄说:
“没有任何东西像牛顿引力理论对行星轨道的计算那样,如此有力地树立起人们对年轻的物理学的尊敬。从此以后,这门自然科学成了巨大的精神王国…… ”
阿基米德在研究杠杆原理后,曾经说过一句什么名言?
“给我一个支点,我可以撬动球。”
那我们又是怎么知道巨大的地球的质量呢?
那给我们一个杠杆(天平)是否就可以称量地球的质量了呢?
答案:不能
测量巨大的天体质量显然只能采用间接的方法.
卡文迪许在实验室称量出了地球的质量!
问题一: 如何测量地球的质量?
思考:卡文迪许是如何“称量”地球的质量的呢?
能否通过万有引力定律来“称量”呢?
时代背景:
当时已知地球的半径R,地球表面重力加速度g及卡文迪许已测出的引力常量G
1.若不考虑地球自转的影响,地面上的物体的重力等于地球对它的引力。
由于g、R在卡文迪许之前已经知道,而卡文迪许测出G后,就意味着也测出了地球的质量。
卡文迪许被称为“第一个称量地球质量的人”!
2.关系式:
3.地球的质量到底有多大?
已知:地球表面g=9.8m/s2,地球半径R=6370km,引力常量G=6.67×10-11N.m2/kg2
请你根据这些数据计算地球的质量M。
代入数据有:
思考:
1.哪些运动的加速度是g?
思考:
2.哪些力的大小与g值有关联?
问题二: 如何测量太阳的质量?
思考:太阳是一个火热的球体,我们无法得知其上的重力加速度,那如何来求太阳的质量呢?
从以下几个方面去考虑:
圆轨道做匀速圆周运动
椭圆
为了解决问题的方便,我们通常可以认为地球在绕怎样的轨道做什么运动?
近似
(1)地球公转实际轨道是什么形状?
(2)地球作圆周运动的向心力是由谁来提供的?
太阳对地球的引力,即F引=F向
(3)动力学方程——万有引力充当向心力
求出太阳的质量
F引=F向 即
明确式中各符号所代表的物理量:
r 代表:
T 代表:
公转轨道半径
公转周期
(4)思考
不需要
相同
②不同的行星r和T各不相同,但计算出来的太阳质量是否一定相同呢?
①测量太阳的质量,是否需要知道行星的质量?
同样的道理,如果已知卫星绕行星运动的周期和卫星与行星之间的距离,也可以算出行星的质量。目前,观测人造卫星的运动,是测量地球质量的重要方法之一。
例1.为了研究太阳演化进程,需知道太阳的质量M.已知地球的半径 R=6.4×106 m,地球的质量 m=6×1024 kg,日地中心的距离 r=1.5×1011 m,地球表面的重力加速度 g=10m/s2,1年约为 3.2×107 s,试估算太阳的质量M.(引力常数未知)
解:由万有引力定律和动力学知识得
对地球表面的物体m′,有
联立两式得
代入数据得
方法一 :测“g”法( 重力近似等于万有引力)
基本思路:
“黄金”代换公式!
根据前面的探究,请同学们归纳总结计算天体的质量的基本思路。
方法二:环绕法 (万有引力充当向心力)
基本思路:
中心天体
环绕天体
M
r
m
能计算月球的质量吗?
只能计算中心天体的质量
不能计算环绕天体的质量
例2、一艘宇宙飞船飞近某一新发现的行星,并进入靠近该行星表面的圆形轨道运行数圈后,着陆在该行星上,宇宙飞船上备有以下实验器材:A.精确秒表一只 B.质量为m的物体一个 C.弹簧秤一只 D.天平一架(包括砝码一套)。已知宇航员在绕行及着陆后各做一次测量,根据所测量的数据可以求出该星球的质量M、半径R(已知万有引力恒量为G)。
(1)两次测量的物理量分别为___________________
(2)两次测量所选用的仪器分别为_______.(用该仪器的字母序号表示).
(3)用所测值可求出星球的质量M=__________
半径R=___________
绕行周期T和物体的重力F
A、C
例3.已知地球与火星的质量之比M地∶M火=8∶1。半径之比R地∶R火=2∶1,在地球表面固定一水平木板,板上再放一个箱子,已知箱子与木板之间的动摩擦因数为0.5,现用水平拉力拖动箱子时,能获得10 m/s2的最大加速度,将箱子、木板送到火星上,仍用同样的力和方式拖动箱子,求此箱子能获得的最大加速度。(g=10 m/s2)
解:在星球表面:
在地球表面拖动,由F合=ma得:
F-μmg地=ma地
在火星表面拖动,同理得:
解上述各式有:a火=μ(g地-g火)+g地=12.5 m/s2
F-μmg火=ma火
问题三: 如何计算天体的密度?
问题三: 如何计算天体的密度?
若T是近地卫星的周期,则r≈R
例4.利用下列哪组数据可以算出地球的质量( )
A、已知地球的半径 R 和地球表面的重力加速度 g
B、已知地球半径R和月球公转周期
C、已知卫星围绕地球运动的轨道半径 r 和角速度ω
D、已知卫星围绕地球运动的线速度 v和周期T
E、已知日地距离及地球绕太阳的公转周期
F、已知地球自转周期和地球半径
G、已知绕地球表面运动的卫星周期T
H、已知绕地球表面运动的卫星周期T和地表g
I、一种地球自转周期T和同步卫星的半径r
ACDHI
例5.利用下列哪些数据可以算出地球的密度( )
A、已知地球的半径 R 和地球表面的重力加速度 g
B、已知地球半径R和月球公转周期
C、已知卫星围绕地球运动的轨道半径 r 和角速度ω
D、已知卫星围绕地球运动的线速度 v和周期T
E、已知日地距离及地球绕太阳的公转周期
F、已知地球自转周期和地球半径
G、已知绕地球表面运动的卫星周期T
H、已知绕地球表面运动的卫星周期T和地表g
I、一种地球自转周期T和同步卫星的半径r
AGH
V0
P
A
2V0
Q
O
H
例6.宇航员站在星球表面上某高处,沿水平方向抛出一小球,经过时间t小球落回星球表面,测得抛出点和落地点之间的距离为L。若抛出时的速度增大为原来的2倍,则抛出点到落地点之间的距离为 。已知两落地点在同一水平面上,求:(1)此星球表面的重力加速度(2)忽略星球自转,若该星球半径为R,求该星球的质量M。
V0
P
A
2V0
Q
O
H
答案:
求:(1)此星球表面的重力加速度(2)忽略星球自转,若该星球半径为R,求该星球的质量M。
例7.《教材》P51 发展空间:估测太阳的密度
所测的物理量:
测量原理:
测量说明:
1、观测时间:
先测质量、再测D和d
地球的公转周期T和测D和d
早晨或傍晚或有保护眼睛的工具
2、测D和d:
小孔成像法
