23.4三角的中位线-华东师大版九年级数学上册课件(16张PPT)
文档属性
| 名称 | 23.4三角的中位线-华东师大版九年级数学上册课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-20 00:00:00 | ||
图片预览

文档简介
(共16张PPT)
§23.4三角形的中位线
知识回顾
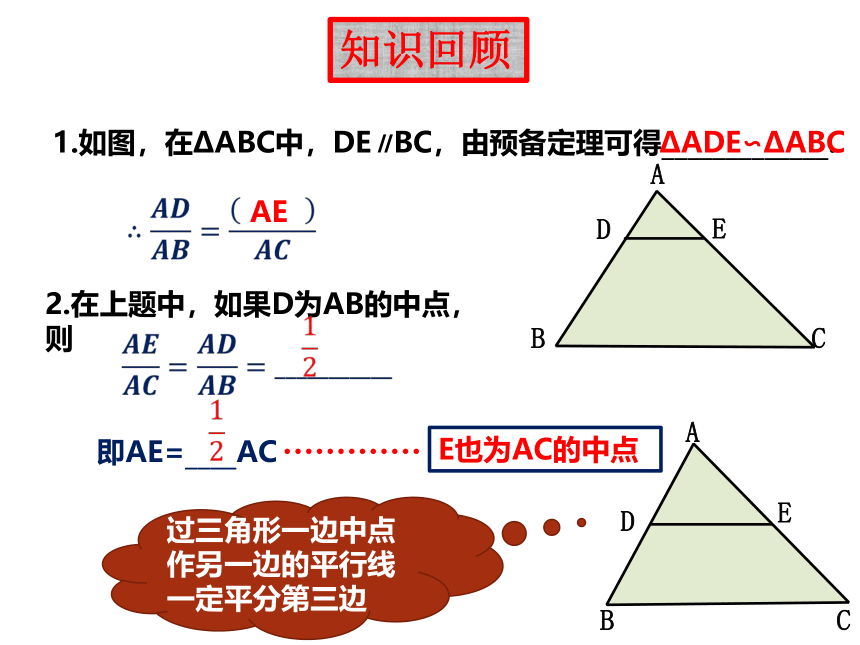
1.如图,在?ABC中,DE∥BC,由预备定理可得_____________.
D
A
B
C
E
?ADE∽?ABC
AE
2.在上题中,如果D为AB的中点,则
即AE=____AC
E也为AC的中点
E
A
B
C
D
过三角形一边中点作另一边的平行线一定平分第三边
知识探索
猜想
E
A
B
C
D
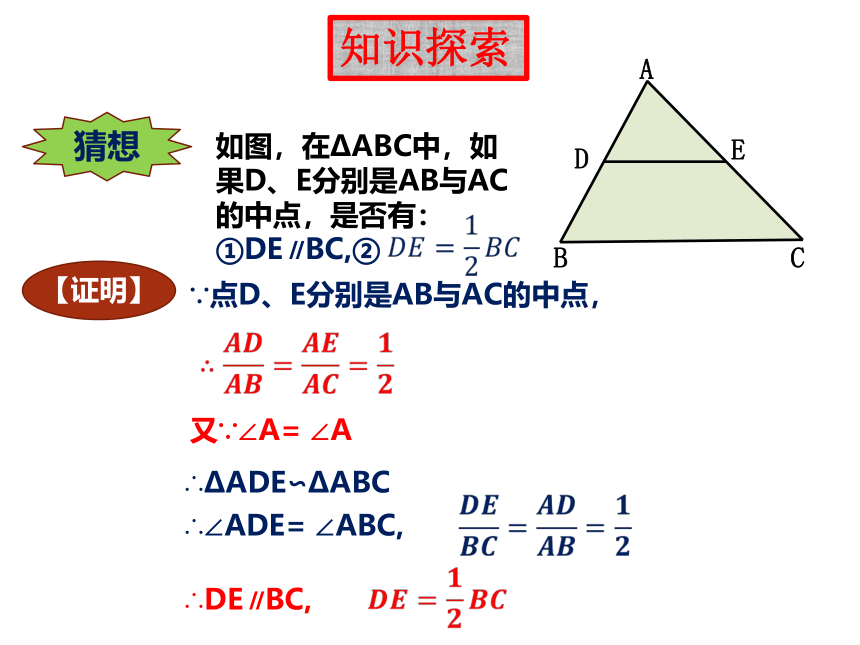
如图,在?ABC中,如果D、E分别是AB与AC的中点,是否有:
①DE∥BC,②
【证明】
∵点D、E分别是AB与AC的中点,
又∵∠A=
∠A
∴?ADE∽?ABC
∴∠ADE=
∠ABC,
∴DE∥BC,
知识概括
知识点1
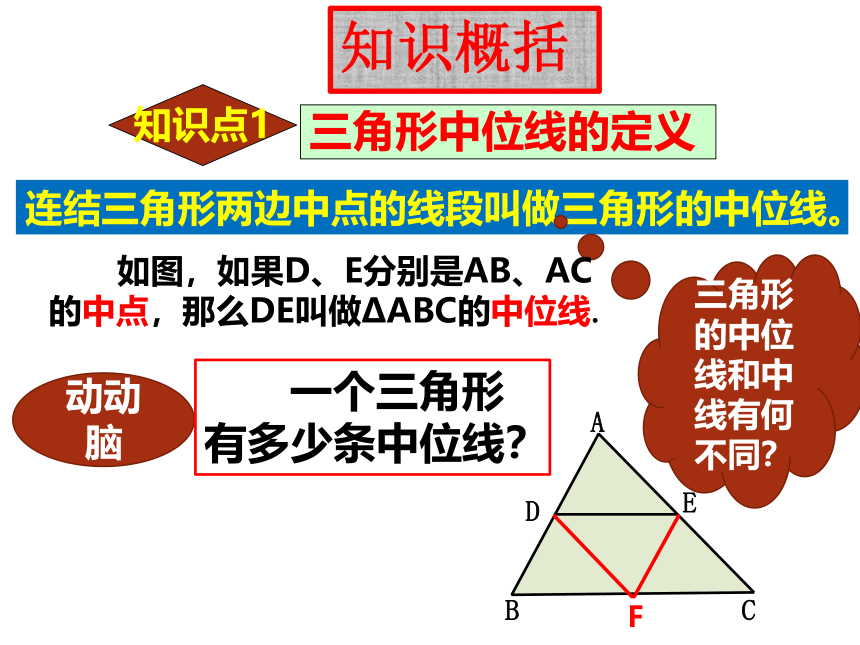
三角形中位线的定义
连结三角形两边中点的线段叫做三角形的中位线。
E
A
B
C
D
三角形的中位线和中线有何不同?
如图,如果D、E分别是AB、AC的中点,那么DE叫做?ABC的中位线.
动动脑
一个三角形有多少条中位线?
F
知识点2
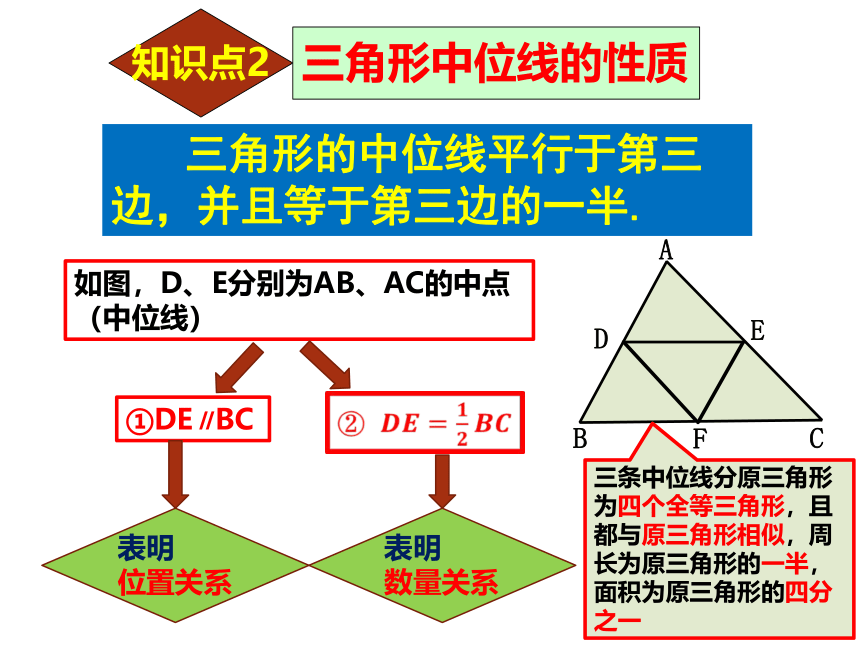
三角形中位线的性质
三角形的中位线平行于第三边,并且等于第三边的一半.
E
A
B
C
D
如图,D、E分别为AB、AC的中点(中位线)
①DE∥BC
表明
位置关系
表明
数量关系
三条中位线分原三角形为四个全等三角形,且都与原三角形相似,周长为原三角形的一半,面积为原三角形的四分之一
F
例题解析
例1
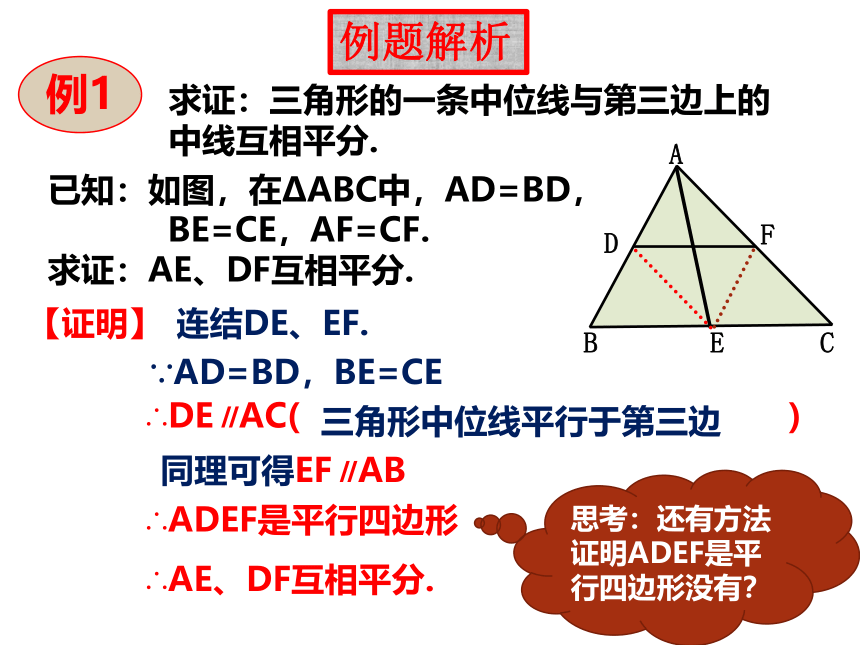
求证:三角形的一条中位线与第三边上的中线互相平分.
F
A
B
C
D
E
已知:如图,在?ABC中,AD=BD,
BE=CE,AF=CF.
求证:AE、DF互相平分.
∵AD=BD,BE=CE
∴DE∥AC(
)
三角形中位线平行于第三边
同理可得EF∥AB
∴ADEF是平行四边形
∴AE、DF互相平分.
思考:还有方法证明ADEF是平行四边形没有?
连结DE、EF.
【证明】
对应练习
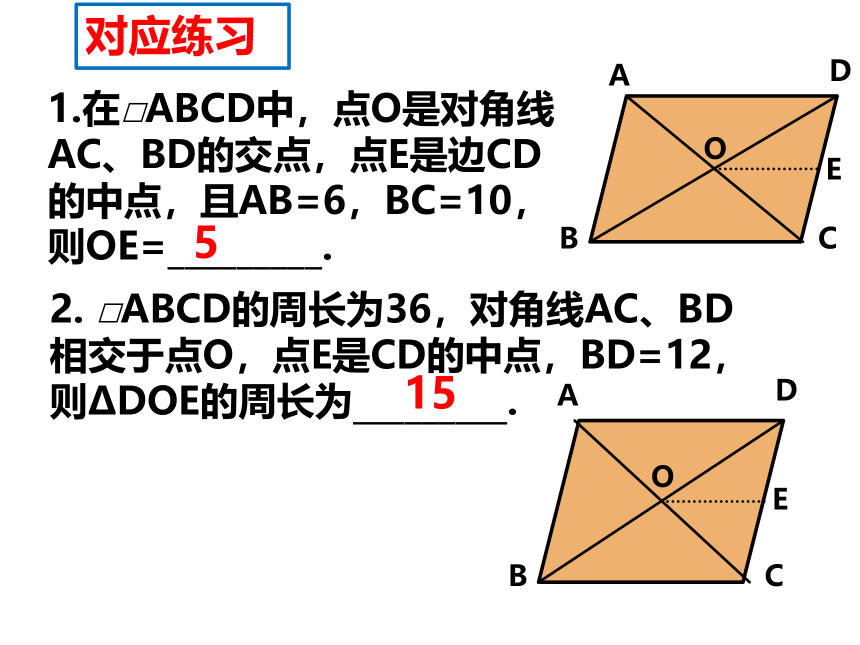
1.在□ABCD中,点O是对角线AC、BD的交点,点E是边CD的中点,且AB=6,BC=10,则OE=_________.
E
A
B
C
D
O
5
2.
□ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则?DOE的周长为_________.
E
A
B
C
D
O
15
3.如图,在四边形ABCD中,点P是边CD上的一个动点,点Q是边BC上的一个定点,连接PA和PQ,点E和F分别是PA和PQ的中点,则随着点P的运动,线段EF的长( )
A.逐渐变大
B.逐渐变小
C.先变小再变大
D.始终不变
D
4.如图,在四边形ABCD中,P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠EPF=140°,则∠EFP的度数是______.
20°
5.求证:顺次连结四边形各边的中点所得的四边形是平行四边形.
A
B
C
D
H
E
F
G
已知:在四边形ABCD中,点E、F、G、H分别为边AB、BC、CD、AD的中点.
求证:四边形EFGH是平行四边形.
【证明】
连结AC
∵E、F是AB、BC的中点,
∴四边形EFGH是平行四边形
判断下列图形四边中点围成的是什么图形?
平行四边形
平行四边形
矩
形
菱
形
菱
形
矩
形
正方形
正方形
拓
展
E
A
B
C
D
G
例2
如图,在?ABC中,D、E分别是边BC、AB的中点,AD、CE相交于点G,
【证明】
连结DE.
∵D、E分别是边BC、AB的中点
三角形的中位线平行于第三边,并且等于第三边的一半
拓
展
实际上,AD、CE
是?ABC的中线,如果再作一条中线BF,同样有:
F
知识概括
知识点3
三角形重心的定义及性质
重心定义:
三角形三边中线的交点
叫做三角形的重心
重心性质:
三角形的重心到一边中点的
距离等于对应中线长的三分之一
E
A
B
C
D
G
F
如图,G为?ABC的重心,则
AG=2GD,BG=2GF
,
CG=2GE
或
AD=3GD,BF=3GF,CE=3GE
对应练习
1.已知如图,AD、BE是?ABC的中线,且AD与BE相交于点P,若AD=6,则AP=_________.
P
A
B
C
D
E
4
2.已知,△ABC中,G是三角形的重心,AG⊥GC,AG=6,GC=8,则△ABC的面积为
.
72
3.如图,在?ABC中,D、E、F分别为边BC、AC、AB的中点,AD、BE、
CF相交于点O,AB=6,BC=10,AC=8.
试求出线段DE、OA、OF的长及∠EDF的大小.(结果保留根号)
O
A
B
C
D
E
F
课堂小结
三角形中位线
连结三角形两边中点的线段叫做三角形的中位线
三角形重心
三角形三边中线的交点叫做三角形的重心
三角形中位线
三角形的中位线平行于第三边,并且等于第三边的一半
三角形重心
三角形的重心到一边的中点的距离等于对应中线长的三分之一
§23.4三角形的中位线
知识回顾
1.如图,在?ABC中,DE∥BC,由预备定理可得_____________.
D
A
B
C
E
?ADE∽?ABC
AE
2.在上题中,如果D为AB的中点,则
即AE=____AC
E也为AC的中点
E
A
B
C
D
过三角形一边中点作另一边的平行线一定平分第三边
知识探索
猜想
E
A
B
C
D
如图,在?ABC中,如果D、E分别是AB与AC的中点,是否有:
①DE∥BC,②
【证明】
∵点D、E分别是AB与AC的中点,
又∵∠A=
∠A
∴?ADE∽?ABC
∴∠ADE=
∠ABC,
∴DE∥BC,
知识概括
知识点1
三角形中位线的定义
连结三角形两边中点的线段叫做三角形的中位线。
E
A
B
C
D
三角形的中位线和中线有何不同?
如图,如果D、E分别是AB、AC的中点,那么DE叫做?ABC的中位线.
动动脑
一个三角形有多少条中位线?
F
知识点2
三角形中位线的性质
三角形的中位线平行于第三边,并且等于第三边的一半.
E
A
B
C
D
如图,D、E分别为AB、AC的中点(中位线)
①DE∥BC
表明
位置关系
表明
数量关系
三条中位线分原三角形为四个全等三角形,且都与原三角形相似,周长为原三角形的一半,面积为原三角形的四分之一
F
例题解析
例1
求证:三角形的一条中位线与第三边上的中线互相平分.
F
A
B
C
D
E
已知:如图,在?ABC中,AD=BD,
BE=CE,AF=CF.
求证:AE、DF互相平分.
∵AD=BD,BE=CE
∴DE∥AC(
)
三角形中位线平行于第三边
同理可得EF∥AB
∴ADEF是平行四边形
∴AE、DF互相平分.
思考:还有方法证明ADEF是平行四边形没有?
连结DE、EF.
【证明】
对应练习
1.在□ABCD中,点O是对角线AC、BD的交点,点E是边CD的中点,且AB=6,BC=10,则OE=_________.
E
A
B
C
D
O
5
2.
□ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则?DOE的周长为_________.
E
A
B
C
D
O
15
3.如图,在四边形ABCD中,点P是边CD上的一个动点,点Q是边BC上的一个定点,连接PA和PQ,点E和F分别是PA和PQ的中点,则随着点P的运动,线段EF的长( )
A.逐渐变大
B.逐渐变小
C.先变小再变大
D.始终不变
D
4.如图,在四边形ABCD中,P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠EPF=140°,则∠EFP的度数是______.
20°
5.求证:顺次连结四边形各边的中点所得的四边形是平行四边形.
A
B
C
D
H
E
F
G
已知:在四边形ABCD中,点E、F、G、H分别为边AB、BC、CD、AD的中点.
求证:四边形EFGH是平行四边形.
【证明】
连结AC
∵E、F是AB、BC的中点,
∴四边形EFGH是平行四边形
判断下列图形四边中点围成的是什么图形?
平行四边形
平行四边形
矩
形
菱
形
菱
形
矩
形
正方形
正方形
拓
展
E
A
B
C
D
G
例2
如图,在?ABC中,D、E分别是边BC、AB的中点,AD、CE相交于点G,
【证明】
连结DE.
∵D、E分别是边BC、AB的中点
三角形的中位线平行于第三边,并且等于第三边的一半
拓
展
实际上,AD、CE
是?ABC的中线,如果再作一条中线BF,同样有:
F
知识概括
知识点3
三角形重心的定义及性质
重心定义:
三角形三边中线的交点
叫做三角形的重心
重心性质:
三角形的重心到一边中点的
距离等于对应中线长的三分之一
E
A
B
C
D
G
F
如图,G为?ABC的重心,则
AG=2GD,BG=2GF
,
CG=2GE
或
AD=3GD,BF=3GF,CE=3GE
对应练习
1.已知如图,AD、BE是?ABC的中线,且AD与BE相交于点P,若AD=6,则AP=_________.
P
A
B
C
D
E
4
2.已知,△ABC中,G是三角形的重心,AG⊥GC,AG=6,GC=8,则△ABC的面积为
.
72
3.如图,在?ABC中,D、E、F分别为边BC、AC、AB的中点,AD、BE、
CF相交于点O,AB=6,BC=10,AC=8.
试求出线段DE、OA、OF的长及∠EDF的大小.(结果保留根号)
O
A
B
C
D
E
F
课堂小结
三角形中位线
连结三角形两边中点的线段叫做三角形的中位线
三角形重心
三角形三边中线的交点叫做三角形的重心
三角形中位线
三角形的中位线平行于第三边,并且等于第三边的一半
三角形重心
三角形的重心到一边的中点的距离等于对应中线长的三分之一
