23.5位似图形-华东师大版九年级数学上册课件(16张PPT)
文档属性
| 名称 | 23.5位似图形-华东师大版九年级数学上册课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-20 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
§23.5
位似图形
知识回顾
我们已经学了图形的哪些变换?
轴对称
平移
旋转
相似
相似与轴对称,平移,旋转一样,也是图形
之间的一个基本变换.可以将一个图形放大或缩小,保持形状不变,得到它的相似图形.
如何便捷地画出一个图形的相似图形呢?
这节课我们学习画相似图形的一种特殊方法.
O
A′
B′
C′
D′
E′
A
B
C
D
E
如图,五边形ABCDE∽五边形A′B′C′D′E′
试一试:对应点的连线有何特点?
这种相似图形称为位似图形
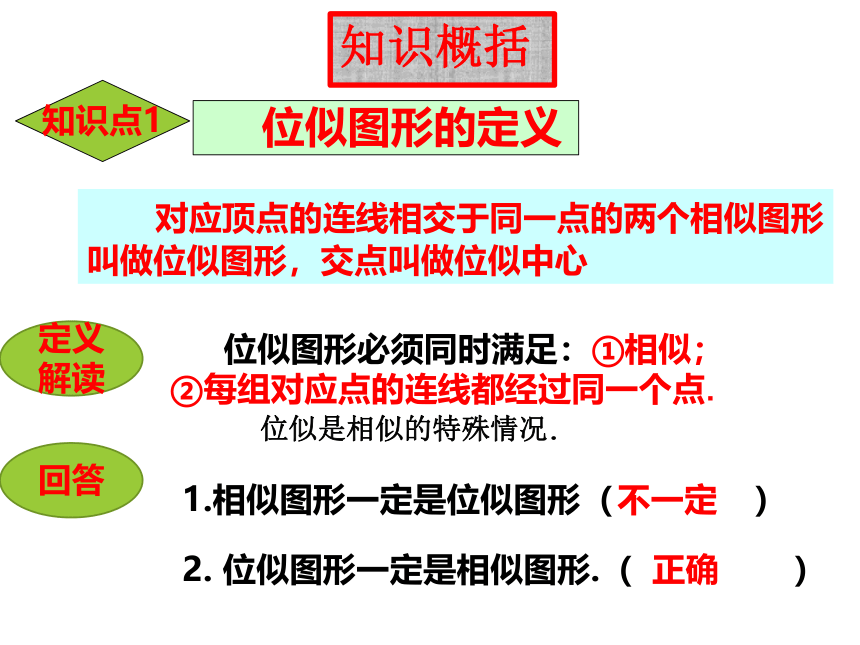
知识概括
知识点1
位似图形的定义
对应顶点的连线相交于同一点的两个相似图形叫做位似图形,交点叫做位似中心
定义解读
位似图形必须同时满足:①相似;②每组对应点的连线都经过同一个点.
回答
1.相似图形一定是位似图形(
)
不一定
2.
位似图形一定是相似图形.(
)
正确
位似是相似的特殊情况.
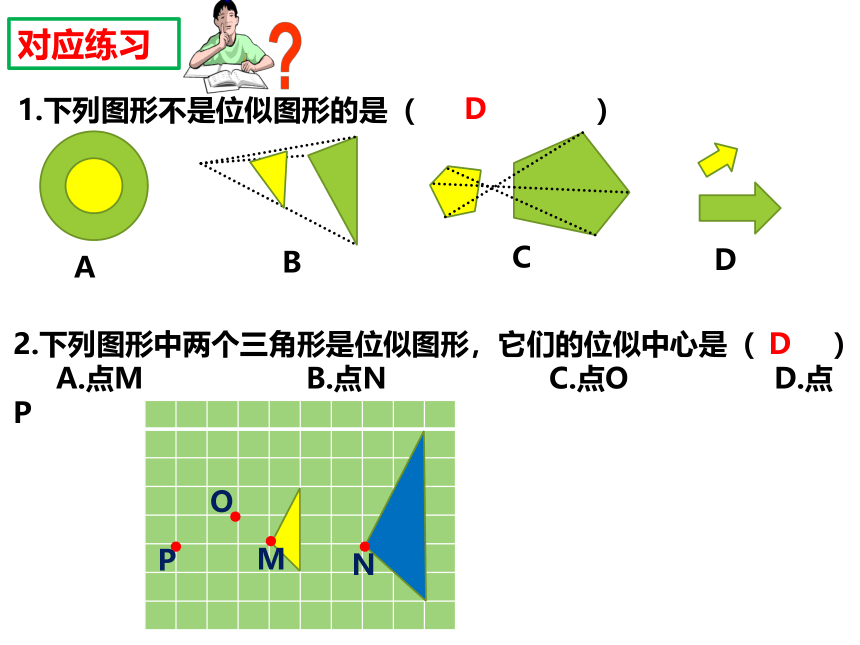
对应练习
1.下列图形不是位似图形的是(
)
A
B
C
D
D
2.下列图形中两个三角形是位似图形,它们的位似中心是(
)
A.点M
B.点N
C.点O
D.点P
?
?
?
?
P
M
N
O
D
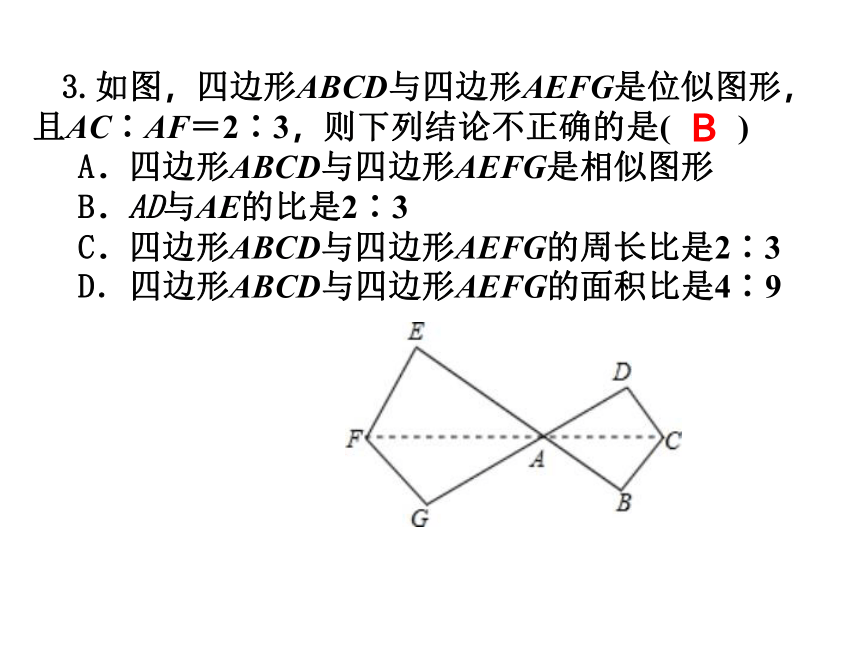
3.如图,四边形ABCD与四边形AEFG是位似图形,且AC∶AF=2∶3,则下列结论不正确的是(
)
A.四边形ABCD与四边形AEFG是相似图形
B.AD与AE的比是2∶3
C.四边形ABCD与四边形AEFG的周长比是2∶3
D.四边形ABCD与四边形AEFG的面积比是4∶9
B
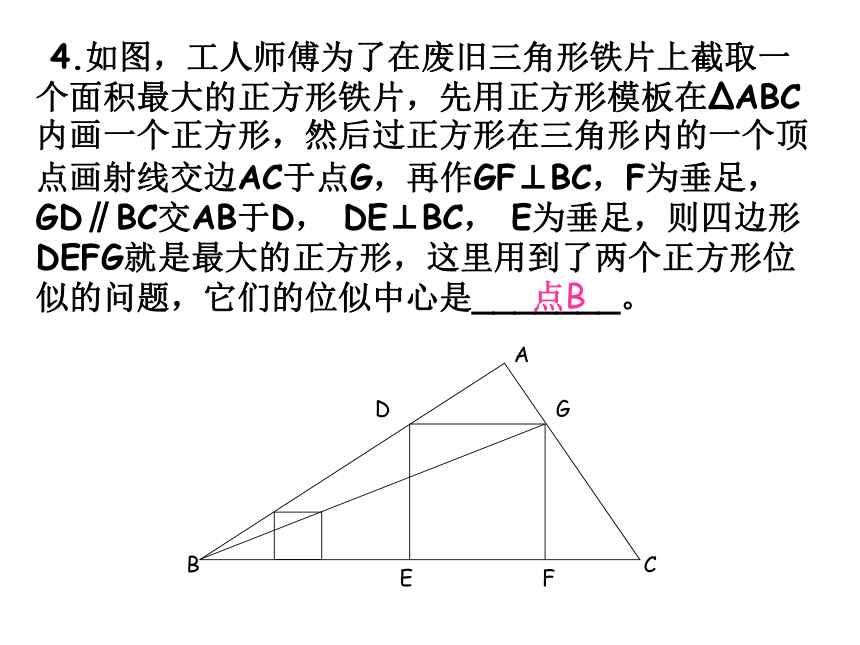
4.如图,工人师傅为了在废旧三角形铁片上截取一个面积最大的正方形铁片,先用正方形模板在ΔABC内画一个正方形,然后过正方形在三角形内的一个顶点画射线交边AC于点G,再作GF⊥BC,F为垂足,GD∥BC交AB于D,
DE⊥BC,
E为垂足,则四边形DEFG就是最大的正方形,这里用到了两个正方形位似的问题,它们的位似中心是_______。
A
B
C
G
F
D
E
点B
如图,任意五边形ABCDE,你能将它放大到原来的1.5倍吗?
A
B
C
E
D
1.任取一点O;
O
2.以点O为端点,作射线OA,OB,OC,OD,OE;
3.分别在射线OA,OB,OC,OD,OE上,取点A′,B′,C′,D′,E′,
使
OA’:OA=OB’:OB=OC’:OC=OD’:OD=OE’:OE=1.5
;
A’
B’
C’
D’
E’
4.连结A’B’,B’C’,C’D’,D’E’,E’A’,得五边形A’B’C’D’E’.
所以,五边形A’B’C’D’E’就是所求作的五边形.
画法:
知识点2
位似图形的画法
?
?
?
?
?
A
B
C
D
E
?
O
画一画:把位似中心取在图形内,将下面图形放大到原来的2倍:
?A′
?B′
?C′
?D′
?E′
你能总结位似作图的步骤吗?
位似作图步骤:
1.确定位似中心;
2.连结位似中心与图形关键点并延长;
3.根据相似比(又叫位似比)确定位似图形的关键点;
4.顺次连结确定的各点.
位似图形上每组对应点到位似中心的距离之比等于相似比
C’
B’
A’
B’
C’
A’
B’
C’
A
B
C
位似中心是
任意
取的,那么除了把位似中心取在形外,还可以取在哪里?
想一想
(1)位似点在△ABC内;
(将△ABC放大两倍)
O
(2)位似点在△ABC的一边上;
A
B
C
A
B
C
.
O
(3)位似点为△ABC的一个顶点.
.
(O)
以上图形还可以怎么画?
画一画:把位似中心取在图形上的A点,将下列图形放大到原来的2倍:
A
B
C
?B′
?C′
位似中心
的取法
A
B
C
E
D
O
A’
B’
C’
D’
E’
观察所画的图,原图形和所画图形位于位似中心的
同侧
能位于位似中心的
吗?
两侧
例:画四边形ABCD的相似图形,使得所画图形与原图形的相似比为2:1,且位于位似中心的两侧.
A
B
C
D
O
A’
B’
C’
D’
对应练习
1.(课本82页练习1)任选一种方法,按下列相似比画出一个三角形的位似图形.
(1) 相似比为1:2
;(2)相似比为2.5.
?
?
?
?
(1)
?
(2)
?
?
?
2.(课本82页练习2)如图,已知格点三角形OAB,请在方格图中画出另一格点三角形,使其与原三角形关于点O成位似关系,并说出它们之间的相似比.
A
B
O
A′
B′
相似比为__________.
2:1
知识点3
位似中心的找法
我们知道,根据位似图形的含义,位似图形每组对应点的连线都经过___________.
位似中心
做一做
找出下列位似图形的位似中心:
?
O
你能总结:位似中心的找法了吗?
连结两组对应点的连线的交点便为位似中心
课堂小结
§23.5
位似图形
知识回顾
我们已经学了图形的哪些变换?
轴对称
平移
旋转
相似
相似与轴对称,平移,旋转一样,也是图形
之间的一个基本变换.可以将一个图形放大或缩小,保持形状不变,得到它的相似图形.
如何便捷地画出一个图形的相似图形呢?
这节课我们学习画相似图形的一种特殊方法.
O
A′
B′
C′
D′
E′
A
B
C
D
E
如图,五边形ABCDE∽五边形A′B′C′D′E′
试一试:对应点的连线有何特点?
这种相似图形称为位似图形
知识概括
知识点1
位似图形的定义
对应顶点的连线相交于同一点的两个相似图形叫做位似图形,交点叫做位似中心
定义解读
位似图形必须同时满足:①相似;②每组对应点的连线都经过同一个点.
回答
1.相似图形一定是位似图形(
)
不一定
2.
位似图形一定是相似图形.(
)
正确
位似是相似的特殊情况.
对应练习
1.下列图形不是位似图形的是(
)
A
B
C
D
D
2.下列图形中两个三角形是位似图形,它们的位似中心是(
)
A.点M
B.点N
C.点O
D.点P
?
?
?
?
P
M
N
O
D
3.如图,四边形ABCD与四边形AEFG是位似图形,且AC∶AF=2∶3,则下列结论不正确的是(
)
A.四边形ABCD与四边形AEFG是相似图形
B.AD与AE的比是2∶3
C.四边形ABCD与四边形AEFG的周长比是2∶3
D.四边形ABCD与四边形AEFG的面积比是4∶9
B
4.如图,工人师傅为了在废旧三角形铁片上截取一个面积最大的正方形铁片,先用正方形模板在ΔABC内画一个正方形,然后过正方形在三角形内的一个顶点画射线交边AC于点G,再作GF⊥BC,F为垂足,GD∥BC交AB于D,
DE⊥BC,
E为垂足,则四边形DEFG就是最大的正方形,这里用到了两个正方形位似的问题,它们的位似中心是_______。
A
B
C
G
F
D
E
点B
如图,任意五边形ABCDE,你能将它放大到原来的1.5倍吗?
A
B
C
E
D
1.任取一点O;
O
2.以点O为端点,作射线OA,OB,OC,OD,OE;
3.分别在射线OA,OB,OC,OD,OE上,取点A′,B′,C′,D′,E′,
使
OA’:OA=OB’:OB=OC’:OC=OD’:OD=OE’:OE=1.5
;
A’
B’
C’
D’
E’
4.连结A’B’,B’C’,C’D’,D’E’,E’A’,得五边形A’B’C’D’E’.
所以,五边形A’B’C’D’E’就是所求作的五边形.
画法:
知识点2
位似图形的画法
?
?
?
?
?
A
B
C
D
E
?
O
画一画:把位似中心取在图形内,将下面图形放大到原来的2倍:
?A′
?B′
?C′
?D′
?E′
你能总结位似作图的步骤吗?
位似作图步骤:
1.确定位似中心;
2.连结位似中心与图形关键点并延长;
3.根据相似比(又叫位似比)确定位似图形的关键点;
4.顺次连结确定的各点.
位似图形上每组对应点到位似中心的距离之比等于相似比
C’
B’
A’
B’
C’
A’
B’
C’
A
B
C
位似中心是
任意
取的,那么除了把位似中心取在形外,还可以取在哪里?
想一想
(1)位似点在△ABC内;
(将△ABC放大两倍)
O
(2)位似点在△ABC的一边上;
A
B
C
A
B
C
.
O
(3)位似点为△ABC的一个顶点.
.
(O)
以上图形还可以怎么画?
画一画:把位似中心取在图形上的A点,将下列图形放大到原来的2倍:
A
B
C
?B′
?C′
位似中心
的取法
A
B
C
E
D
O
A’
B’
C’
D’
E’
观察所画的图,原图形和所画图形位于位似中心的
同侧
能位于位似中心的
吗?
两侧
例:画四边形ABCD的相似图形,使得所画图形与原图形的相似比为2:1,且位于位似中心的两侧.
A
B
C
D
O
A’
B’
C’
D’
对应练习
1.(课本82页练习1)任选一种方法,按下列相似比画出一个三角形的位似图形.
(1) 相似比为1:2
;(2)相似比为2.5.
?
?
?
?
(1)
?
(2)
?
?
?
2.(课本82页练习2)如图,已知格点三角形OAB,请在方格图中画出另一格点三角形,使其与原三角形关于点O成位似关系,并说出它们之间的相似比.
A
B
O
A′
B′
相似比为__________.
2:1
知识点3
位似中心的找法
我们知道,根据位似图形的含义,位似图形每组对应点的连线都经过___________.
位似中心
做一做
找出下列位似图形的位似中心:
?
O
你能总结:位似中心的找法了吗?
连结两组对应点的连线的交点便为位似中心
课堂小结
